基于残余应力和应力集中系数的凹坑细节疲劳额定值预测

施剑玮， 殷之平

(1.上海飞机设计研究院， 上海 201210； 2.西北工业大学航空学院， 西安 710072)

冲击凹坑是飞机金属机身蒙皮日常运营过程中经常发生的一种损伤形式，因冰雹、外来物冲击、维护时工具碰撞等在机身蒙皮表面产生永久塑性变形，形成凹陷。凹坑将引起金属机身蒙皮外表面产生新的残余应力和应力集中，显著降低飞机结构的疲劳寿命，对飞机的安全运营影响很大。

有学者对相关的凹坑进行了研究和探讨。周广洲[1]阐述了凹坑的一般形状、尺寸和相应的维护检查要求；纪晓懿等[2]从应力集中的角度研究了薄壁圆筒压力容器凹坑的疲劳寿命模拟计算；邝临源等[3]给出了一种凹陷结构的疲劳寿命的快速算法；刘猛[4]从疲劳S-N(stress-number)曲线的角度，阐述了金属凹坑冲击对疲劳寿命影响试验研究及其疲劳寿命预测；詹志新等[5]对钛合金壁板冲击凹陷的疲劳寿命预估进行了研究；Bellett等[6]研究了三维应力集中系数对疲劳性能的影响，Li等[7]研究了冲击后凹坑的残余应力的影响。总体说来，极少有从考虑残余应力和应力集中共同影响的角度出发，对适用于工程计算的方法进行研究，传统的分析方法[8-9]忽略了残余应力的影响，导致分析结果偏于危险。

采用有限元数值方法对冲击能量与凹坑尺寸系数之间的关系进行研究，并通过试验予以验证。此外，对凹坑不同尺寸系数的残余应力和应力集中系数进行研究，提出了一种用于飞机金属机身蒙皮凹坑的疲劳分析方法，适用于工程应用。

1 蒙皮凹坑冲击的影响研究

蒙皮凹坑长度(L)是指从凹坑一端到另一端的最长距离，宽度(W)是指垂直于凹坑长度方向上的最长距离，最大深度Y是指凹坑偏离原始轮廓的最大距离。凹坑的疲劳性能对蒙皮厚度和凹坑长度不敏感(蒙皮厚度很薄，通常为1.27～1.60 mm)，在飞机结构修理手册中，允许的损伤仅与凹坑的尺寸系数，即宽/深比(W/Y)相关，凹坑示意图如图1所示。

1.1 冲击凹坑试验及结果

使用落锤式冲击台，用钢制冲击头冲击2524-T3铝合金方板试验件[10]，如图2所示，测量和记录不同冲击能量形成的凹坑的尺寸系数(W/Y)，根据试验数据，获得冲击能量与凹坑的尺寸系数(W/Y)之间的试验曲线，如图3所示。

图1 凹坑尺寸示意图Fig.1 The dent size sketch

图2 试验件凹坑照片Fig.2 Photograph of testing dent

图3 试验曲线Fig.3 Test curve

1.2 有限元数值计算

使用Abaqus动力学模块进行冲击仿真，得到冲击能力与凹坑的尺寸系数之间的关系，并与试验结果相比，得到试验与分析的曲线，如图4所示。

随着冲击能量不断增大，尺寸系数越来越小，图4给出有限元与试验得到的冲击能力与尺寸系数关系，两种吻合很好。

图4 试验和分析曲线Fig.4 Test and analysis curves

2 凹坑修正的疲劳分析方法

采用有限元数值方法，计算凹坑不同的尺寸系数W/Y=30、20、15、10的情况，对应力集中系数和残余应力的变化进行研究。

2.1 残余应力计算

金属薄板受到冲击后，凹坑附近发生永久变形后形成残余应力，通过有限元数值分析计算残余应力的大小，冲击的不同时刻，薄板表面的应力云图如图5所示。

图5 冲击过程中的应力分布Fig.5 The stress distribution during impact process

冲击球弹起稳定后，受冲击面为残余拉应力，背部为残余压应力。由表1可知，经过计算，可以得到不同尺寸系数下应力集中位置的残余应力随W/Y减小有增大的趋势。

经过探索性因子分析，该量表的克伦巴赫信度系数为0.800，KMO值为0.865，说明这七条陈述项目适合做因子分析，量表内部的一致性和稳定性较好。

2.2 应力集中系数计算

冲击形成凹坑的应力集中系数与材料变形本身无关，与冲击后的凹坑尺寸系数和形成的凹坑的受载形式有关，现计算不同尺寸系数的薄板在轴向拉伸情况下，凹坑附近的应力集中系数，如图6所示。

表1 残余应力计算结果Table 1 Calculation results of residual stress

图6 不同尺寸系数的应力集中系数Fig.6 The stress concentrations of different size factors

由图6可知，凹坑受冲击面(即上表面)在轴向拉伸时受拉，而凹坑背面在轴向拉伸时受压应；凹坑的拉升应力最大点即应力集中并非在凹坑中心，而是在凹坑中心附近区域，不同尺寸系数的应力集中点位置也不同；总体来讲，应力集中系数随W/Y不断减小而增大，具体如表2所示。

表2 应力集中计算结果Table 2 Calculation results of stressconcentration

2.3 凹坑修正的疲劳分析方法

参看文献[8]，关于金属材料的疲劳等寿命曲线关系如图7所示。

σa为应力幅值；σm为平均应力；R为应力比；N为寿命； DFR为细节疲劳额定值图7 等寿命曲线Fig.7 Photograph of equal life curve

将传统的疲劳分析方法[8]进行修正，如式(1)、式(2)所示：

(1)

(2)

式中：σm0为静载破坏应力；Δσm为应力谱中增加的平均应力；DFR为未冲击蒙皮的细节疲劳额定值；DFR′为受冲击蒙皮的细节疲劳额定值。

残余应力是蒙皮表面未承受飞机的服役载荷之前，仅由于冲击凹坑引入的结构内应力，正常进行飞机结构的疲劳分析时，残余应力仅增加了飞机疲劳交变应力谱中的平均应力，而未改变服役载荷产生的应力幅值，因此平均应力的增加可用式(3)来表示。

(3)

(4)

(5)

式(5)中：DFRbase为材料基准细节疲劳额定值；Rc为细节疲劳额定系数；Kt0基准应力集中系数。

3 试验与分析结果比较

3.1 疲劳试验

根据冲击能量与尺寸系数关系，分别预制尺寸系数W/Y=30、15、10的2524-T3铝合金试验件3组，每组20件，每组的疲劳试验最大应力从大到小分为4级，应力比R=0.06，每级试验件有5件，试验照片如图8所示。

图8 疲劳试验件照片Fig.8 Photograph fatigue testings

3.2 分析计算

对疲劳试验的寿命数据进行处理，计算得到DFR，并与分析的结果进行比较，如表3、图9所示。

表3 试验与分析结果Table 3 Test and analysis results

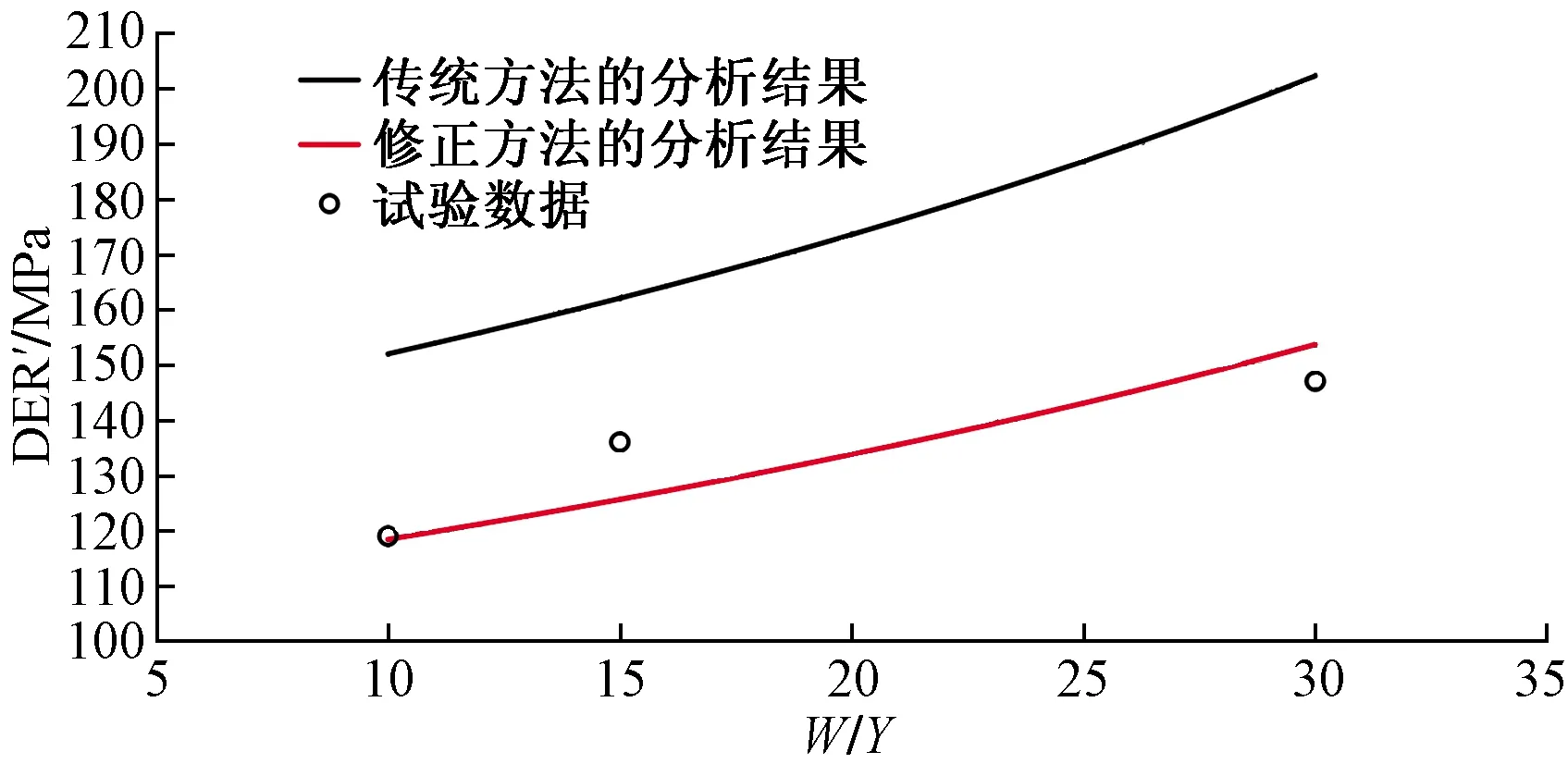
图9 DFR的分析与试验结果比较Fig.9 Comparison of test and analysis results of DFR

4 结论

采用有限元法分析和试验验证的方法进行了冲击能量与凹坑尺寸系数的研究，通过凹坑的应力集中和残余应力分析，提出了一种修正的凹坑疲劳分析方法，并与试验数据进行对比，得出如下结论。

(1)凹坑尺寸系数由低速冲击的能量决定，随着冲击能量不断增大，凹坑的尺寸系数逐渐变小，在W/Y接近10时趋于稳定。

(2)应力集中系数和残余应力大小由凹坑尺寸系数决定，随着凹坑尺寸系数不断增大，应力集中系数和残余应力都逐渐减小。

(3)传统分析方法的结果与试验数据的比值在1.19～1.37，偏于危险；修正的分析方法的结果与试验数据的比值在0.93～1.05，基本是保守的，误差很小。

(4)修正的分析结果与试验数据吻合很好，最大误差为7%，完全满足工程应用。