基于邻近频点插值混合扩频信号多普勒频偏估计算法*

王东政， 李双喜， 郑二矿， 崔 嵬

(1. 北京理工大学 信息与电子学院， 北京 100081； 2. 北京航天自动控制研究所， 北京 100854)

为了满足未来信息对抗等新形式的需求，测控通信系统需要具备强大的抗干扰和抗截获能力.在复杂的电磁环境中，直接序列扩频(DSSS)只能提供有限的抗干扰性，难以对抗对准式干扰>和全频带干扰[1].直扩、跳扩混合扩频系统结合了直接序列扩频和跳频扩频两者的优点，作为新一代扩频通信技术，以其可靠性和通用性在通信领域得到广泛认可.

信号的多普勒频偏反映了信源与接收机间的相对速度，所以多普勒频偏的测定有着重要意义.目前，有关多普勒频偏估计方法的研究主要基于时域或频域而展开[2]，基于时域的估计方法存在计算复杂、同步速度慢等缺点，因而研究者倾向于计算量更小的频域估计方法[3]，这类估计方法主要通过快速傅里叶变换(FFT)实现，其估计依据是FFT的峰值谱线对应着待估计频率值.不过，由于FFT栅栏效应的存在，使得这类方法只有在待估频率是频域分辨率的整数倍时才能获得较为准确的估计结果.解决这一问题的主要方案是基于插值或频谱细化的改进FFT算法，如Rife算法[4]，Zoom-FFT算法[5]和基于最大功率搜索的方法[6]，这些算法都极大地提高了多普勒频偏的估计精度，但计算量也随之提高[7].针对这一问题，本文采用了一种针对直扩、跳扩混合扩频的频率估计算法提高频率估计精度.该算法在不增加硬件规模的情况下，利用捕获到的频率点以及其前后等间隔的多个频率点处的信号强度来实现频率估计.

1 混合扩频信号检测

混合扩频捕获算法的链路框图如图1所示.伪码I的码速率控制接收端同步信息的长度，伪码II控制载波频率变化速度的快慢.

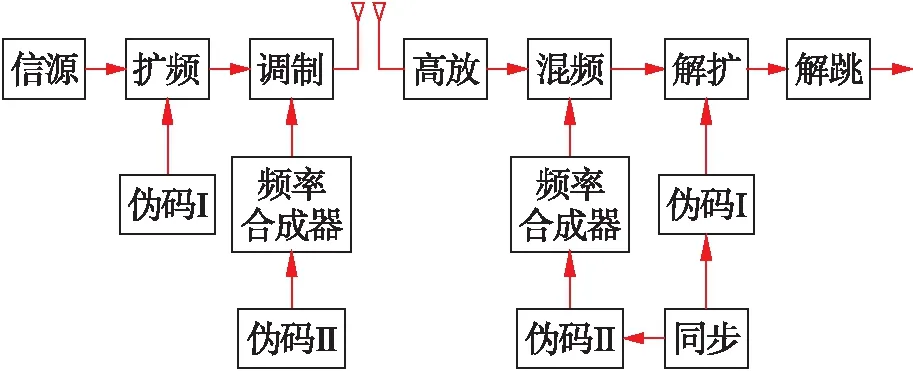
图1 混合扩频系统发射/接收链路框图Fig.1 Block diagram of transmit/receive link of hybrid spread spectrum system

伪码序列(PN码)I首先将要传输的信号进行采样扩频，然后PN码II控制频率合成器进行载波跳频控制，射频信号经过放大后被发送.在接收端，首先进行解跳，在本地产生相同跳频图案的载波，将接收到的高频跳频信号转换成固定载波频率的中频信号，然后通过频域并行码相位串行的方式进行解扩，恢复出原始信号.混合扩频系统包含两种扩频码，一种用于直接序列扩频，另一种用于频率合成器的控制.为方便DSSS信号的捕获，跳频设计多采用慢跳策略，应用于直扩信号的伪码速率远高于应用于跳频信号的伪码速率.

混合扩频模型的直接序列扩频部分采用基于FFT的频域并行码相位串行捕获算法，算法原理图如图2所示.该搜索算法能够同时完成对多个频点的搜索，快速捕获具有较大多普勒频偏的高动态混合扩频信号.DSSS信号捕获过程中，相关峰值与相干累积时间关系[8]如图3所示，因此通过对上述多个频点的相关值进行分析，可以估计出多普勒频偏.

图2 直接序列扩频捕获算法原理图Fig.2 Principle diagram of DSSS acquisition algorithm

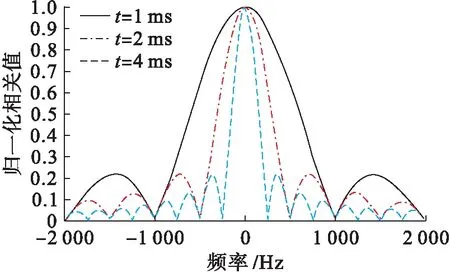
图3 相干累积时间对相关值的影响Fig.3 Effect of coherent cumulative time on correlation value

接收端收到的跳频信号可表示为

gTC(mTs-kTC)

(1)

(2)

式中：A为信号幅度；C(·)为伪码序列I；τ为伪码偏移量；ζ为多普勒频率对码速率偏移的影响因子；ωIF=2πfIF为中频信号角频率；ωd=2πfd为多普勒角频率；ωk为跳频频率；φ0为载波相位；N(·)为传播过程中的高斯噪声；Ts为采样时间间隔；TC为通带宽度.

接收端混频后的输出信号可近似表示为

s(m)=AC[(1+ζ)mTs+τ]·

cos[ωdmTs+φ0]+N(mTs)

(3)

为了对混频输出信号进行正确的解扩，准确地估计出多普勒频偏ωd的值至关重要，本文算法即为解决这一问题而设计.

2 多普勒频偏估计

为了准确估计出接收信号中的多普勒频偏，本文采用了一种基于邻近频点插值的多普勒频偏估计算法，其主要思想是：在完成捕获所有频点操作的基础上，找出峰值谱线对应的频点，利用该频点前后两个相邻频点的FFT变换值对峰值频点进行多普勒频偏修正，最终通过谱线和多普勒频率值的比例关系确定接收端的同步载波频率.

首先，在本地接收端产生两路相位差为90°的信号Ip(m)和Qp(m)，用于信号解跳，其表达式为

gTC(mTs-kTC)

(4)

gTC(mTs-kTC)

(5)

其次，对式(1)进行下变频以及积分清除操作，忽略码的多普勒频率和下变频中的高频项，其表达式为

cos(ωdmTs+φ0)+NI(mTs)=

(6)

sin(ωdmTs+φ0)+NQ(mTs)=

(7)

基于I(n)和Q(n)构建一个复信号z(n)=I(n)-jQ(n)，然后对其进行M点FFT变换(M≥P)，由此得到

(8)

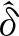
(9)

假设p=1/MLTs为谱线和多普勒频率值的线性比例，则修正后的多普勒频偏估计值为

(10)

3 仿真验证

3.1 仿真条件

结合工程实际，本文仿真使用的相关参数如表1所示.仿真过程采用模平方积累6次的非相干累积算法，相参积累时间为2 ms，统一保存模平方积累的结果.相关峰与多普勒频率偏移和码相位偏移的关系如图4所示.

3.2 信噪比变化对频偏估计的影响

仿真中设置的多普勒频率为1 634 Hz，伪码相位为135.1，信噪比变化范围为从-27～-1 dB，步进值为2 dB，每个信噪比工况下都做3 000次蒙特卡罗仿真.频率均方根误差与信噪比的关系曲线如图5所示.

表1 仿真模型参数Tab.1 Simulation model parameters

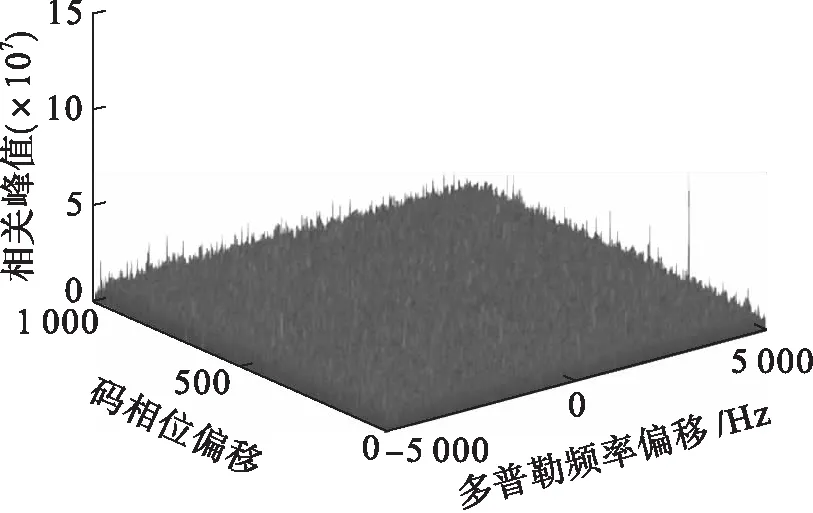
图4 相关峰与多普勒频率偏移和码相位偏移的关系Fig.4 Relationship between correlation peak，Dopplerfrequency offset and code phase offset

图5 捕获频率均方根误差与信噪比的关系Fig.5 Relationship between acquisition frequency root-mean-square error and SNR

由图5可以看出，在信噪比小于-23 dB时，扩频信号检测系统处于虚警状态，因此均方根误差很大.当信噪比达到-23 dB时，均方根误差显著减小，并随着信噪比的提高会继续逐渐改善，在信噪比较高的情况下，插值算法的均方根误差要明显好于非插值算法.

在非插值算法中，随着信噪比的改善(当信噪比高于-23 dB时)，均方根误差不能显著减小，这意味着传统的非插值捕获方法在信道状况良好的情况下多普勒频率捕获的精度取决于采样频率.

通过将混合扩频信号捕获的频率与设定的频率进行比较，得到偏差结果.由于-25和-27 dB信噪比下处于虚警状态，故统计-23～-1 dB之间的分布结果如图6所示(曲线是3 000次捕获结果与真值偏差的平均值，因需要判断多普勒频率估计值与临近频点间关系，求整体偏差统计过程中单次偏差取绝对值).

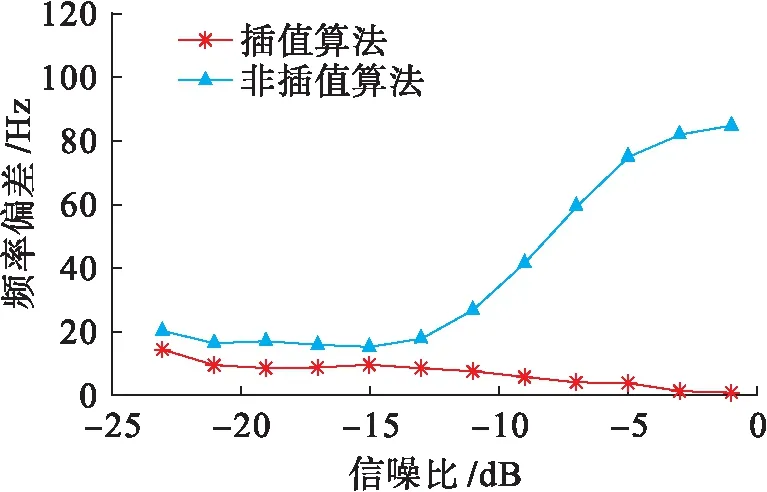
图6 捕获频率偏差与信噪比的关系Fig.6 Relationship between acquisition frequency offset and SNR

图6中，插值算法3 000次蒙特卡罗频率估计的平均偏差值总是小于20 Hz.随着信噪比的提高，频率估计的偏差分布更接近0 Hz，这与在均方根误差分布中得到的结论是一致的.此外，还可以看到，即使在-23 dB的最坏工作条件下，平均偏差仍然小于非插值算法下的频率捕获精度，这表明插值算法在低信噪比下的有效性.

在非插值算法下，由于栅栏效应的存在，多普勒频率捕获精度为250 Hz，仿真过程设定的频率为1 634 Hz，位于1 500和1 750 Hz之间.无论信噪比大小如何，捕获的结果只能是1 500或1 750 Hz，这导致捕获的频率偏差将始终存在，即使在无噪声条件下也是如此.此外，随着信道环境的改善，单次捕获到的结果将有更多的是偏差较小的频率值，而非均匀分布，在捕获频率平均值上的表现将更倾向于偏差较小的频率值，从而导致整体捕获偏差的平均值增加.在本次模拟中，1 634与1 750 Hz间的偏差更小，非插值算法捕获到的频率值随着信噪比的改善会更倾向1 750 Hz，反映在非插值算法捕获频率偏差平均值的曲线趋势上.

3.3 频率变化对频偏估计的影响

在非插值算法中，频率捕获精度为250 Hz，当频率变化范围为3 996～4 496 Hz时，捕获结果只能是4 000、4 250或4 500 Hz.这种阶梯式的搜索结果必然会引入较大的舍入误差，而本文所采用的插值算法通过插值方式进行频偏估计，可以有效地消除这种舍入误差.针对频率变化的仿真在信噪比分别为-20和-5 dB的两种典型工况下，且频率范围在4 000～4 500 Hz的频带内进行，插值估计算法设定的频率步进值为20 Hz.频偏估计均方根误差和频率偏差的仿真结果分别如图7～8所示.

图7 均方根误差与频率的关系Fig.7 Relationship between root-mean-square error and frequency

如图7所示，随着频率的变化，本文采用的插值频偏估计方法捕获频率均方根误差分布没有显著变化，不受捕获电路接收到信号频率变化的影响.从图8中对比可以观察到，捕获频率平均偏差始终分布在0 Hz左右，-20 dB的频率平均偏差大于-5 dB的频率平均偏差，且-5 dB的平均波动相对较小，平均频率偏差更接近0 Hz，符合预期.然而，在非插值算法下由于存在250 Hz的频率捕获精度限制，捕获结果的均方根误差和捕获频率偏差平均值受给定频率变化的影响很大，它们会随着设定频率值和可以捕获到的临近频率值之间的差值变化而周期性地变化.

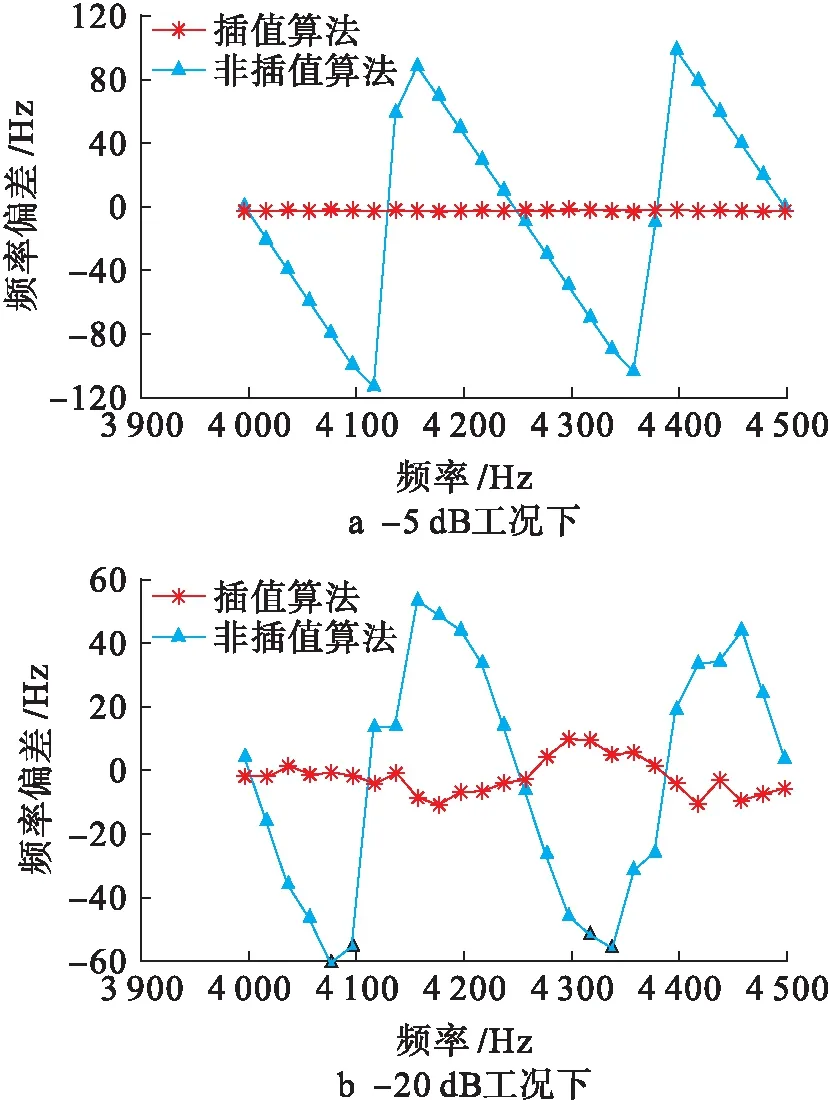
图8 捕获频率偏差与频率的关系Fig.8 Relationship between acquisition frequency offset and frequency

4 结 论

本文采用一种基于直扩、跳扩混合扩频信号的多普勒频偏估计算法，利用傅里叶变换后各频点之间的相关峰值关系，通过插值算法完成多普勒频偏估计.该算法可并行捕获给定范围内的所有频率，且不需要较多改变电路结构.仿真结果表明，该算法可以提供更准确的频率估计，捕获电路接收到信号的多普勒频率并不显著影响所述算法的估计精度.