基于梯度下降法的翼伞系统最优分段航迹规划

陈奇，赵敏，李宇辉，何紫阳

1. 淮阴工学院 电子信息工程学院，淮安 223003 2. 南京航空航天大学 自动化学院，南京 210016

冲压式翼伞是一种由纺织材料构成的柔性飞行器，开伞后空气由翼伞前缘切口进入气室，在气室内形成滞止压力，使翼伞能保持较为稳定的翼形并产生升力和阻力，因此翼伞具有较高升阻比、优良的滑翔性能和可控性[1]。拉拽伞衣后缘可以调整翼伞飞行方向和速度，实现精确着陆，克服了传统圆形降落伞飞行轨迹随风飘、落点散布大的缺点，同时翼伞在着陆时可以以雀降方式无损着陆，在战场物资精确空投、自然灾害救灾物资精确空投、航天器回收等领域有广泛应用前景，得到了国内外许多研究者的关注[2]。为翼伞系统规划出合适归航航迹是能否实现精确空投的前提之一，很大程度上决定了翼伞的着陆精度和归航控制方式，只有在合适的规划航迹的基础上才能设计合适的航迹跟踪控制器，因此航迹规划对实现翼伞精确空投具有重要意义。

翼伞系统航迹规划是指在翼伞动力学约束基础上，为翼伞系统规划出从初始空投点到目标点的、满足特定性能指标的归航航迹。早期归航主要为径向归航和锥型归航，由于其归航精度较低，现已较少采用，目前主要的翼伞系统航迹规划方法为最优控制归航法和分段归航法。

最优控制归航法以准确、安全、控制能量小等为优化目标，求解算法主要包括间接法和直接法，熊菁[3]采用间接法求解了翼伞系统的最优航迹规划问题，利用极小值原理将最优控制问题转化为两点边值问题再求解，但该方法需要先对状态方程进行正向积分，再对协态方程进行反向积分，过程较为繁琐复杂。高海涛[4]、罗淑贞[5]、Sun[6]等运用直接法求解了翼伞最优控制归航航迹规划问题，主要利用伪谱法将最优控制航迹规划问题转化为非线性规划问题，再利用序列二次规划算法求解该问题。Zhang等[7]利用伪谱法求解了翼伞航迹规划问题，并利用粒子群优化(Particle Swarm Optimization，PSO)算法确定Pareto优化点，进一步改进了航迹规划效果。Weinstein等[8]直接利用PSO算法实现了翼伞鲁棒制导，规划的航迹可有效降低翼伞着陆误差和着地冲击速度。陶金等将最优控制航迹规划问题转化为B样条基函数控制顶点的参数优化问题，然后采用遗传算法[9]或量子遗传算法[10]等智能算法进行目标函数寻优。梁海燕[11]、蒋华晨[12]等基于敏感度分析方法，利用控制变量参数化与时间尺度相结合的优化算法，将航迹规划问题转化为一系列参数优化问题再进行数值求解。需要指出的是，这类最优控制航迹规划方法获得的最优控制量往往都是连续的。

分段归航法由于操纵过程简单、鲁棒性强，因此在X-38等系统中得到了实际应用。熊菁等[13]基于遗传算法，研究了翼伞系统的分段归航航迹设计问题，规划的航迹被分段为目标接近段、能量控制段和逆风着陆段，目标接近段和逆风着陆段主要实施滑翔运动、能量管理段主要为螺旋线下降的转弯运动。张兴会和朱二琳[14]基于改进粒子群算法设计了翼伞系统分段归航航迹，仿真表明设计的归航轨迹简单实用，满足落点精度要求。郑成等[15]基于改进遗传算法(Improved Adaptive Genetic Algorithm，IAGA)有效求解了分段归航轨迹问题，提出的算法可有效防止早熟，收敛速度更快，规划的航迹满足定点和逆风着陆的要求。陶金等[16]基于粒子群算法优化了分段归航轨迹，并采用线性自抗扰控制器(Linear Active Disturbance Rejection Controller，LADRC)对航迹进行了修正，仿真结果表明该归航控制可提高抗风性能和归航精度。赵志豪等[17]基于人工鱼群算法对分段航迹目标函数进行了参数寻优，提出的算法可加快算法收敛速度，规划航迹满足精确落点和逆风着陆的要求。上述分段归航算法采用的目标函数大同小异，都是将航迹规划问题转化为进入点(Entry Point)参数的优化问题，尽管采取的算法在收敛速度方面有差异，但得到的结果是大致相同的，都能满足精确着陆和逆风着陆要求。需要注意的是，分段归航算法的优化函数中一般不包含能耗指标，因此分段归航法在能量消耗方面不占优势，此外，获得的航迹中包含多个半径最小的过渡转弯段，此时需要突然将控制绳下拉到最大量，然后短时间内又将其恢复到较小控制量，这对翼伞的实际操控提出了更高的要求。

为进一步改进翼伞系统航迹规划效果，本文提出了一种基于梯度下降法的最优分段航迹规划算法。在考虑翼伞初值约束、终点逆风精确着陆约束、控制约束、障碍规避约束情况下，将控制变量参数化为一系列分段常值，在翼伞质点模型状态方程约束下，将航迹规划问题转化为优化问题，然后利用梯度下降法求解该优化问题。通过和基于伪谱法求解的最优控制规划航迹、基于遗传算法的分段归航航迹对比，可以发现三者在相同条件下都能满足精确、逆风着陆要求，但本文算法得到的航迹能量消耗更低，且控制量由分段常值构成，简化了翼伞归航时的操控，同时控制量的值在一个较小范围内变化，为系统提供了更大的控制量冗余，有利于航迹跟踪控制时的偏差修正。在进一步考虑避障约束后，本文算法规划的航迹可以实现对山峰障碍的绕行，获得的航迹平滑合理，便于跟踪。

1 翼伞质点模型

翼伞模型涉及到翼伞的动力学方程和运动学方程，包括翼伞的升力、阻力、表观质量等多个因素，具有高非线性和强耦合性。常用翼伞模型有4自由度、6自由度、9自由度等不同自由度的模型[18]，模型自由度越高，可获得的状态参量就越多，但其计算复杂度也就越高，在不需要研究翼伞载荷相对于伞衣的相对运动，仅需研究翼伞系统整体的期望航迹时，可将系统整体看作质点，用翼伞质点模型代替复杂的高自由度模型实现航迹规划。对翼伞系统而言，最佳升阻比对应某个对称下偏量，该对称下偏量记为基准稳态下偏量，控制算法将在基准量附近产生非对称下偏指令：在降低翼伞一侧后缘的同时，以相同角度提升另外一侧后缘，此时滑翔比随双侧非对称下偏量的变化较小[19]，可做如下假设：

1) 在翼伞作基准稳态飞行情况下，翼伞滑翔比和飞行速度可视为常数，在考虑翼伞的控制时，以非对称后缘下拉的转弯控制为主。

2) 考虑风场为水平风场，风场可预知，风的效果只引起位置的偏移，此时可将风向和风速的影响转化为初始点的位置偏移。

3) 翼伞对控制输入的影响无延迟。

在上述假设下，可得到翼伞在风固定坐标系下的降阶质点模型：

(1)

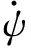
2 最优控制航迹规划问题描述

翼伞系统最优控制航迹规划问题的优化目标主要包括如下几点：① 最终着陆点到目标点的着陆误差最小；② 翼伞着陆时的方向为逆风方向，以减小着陆速度，降低翼伞系统着陆冲击；③ 归航过程中的能量消耗最小；④ 翼伞在归航过程中能躲避障碍。在满足这几个指标的同时，规划航迹的控制量还必须小于等于容许控制量。综合考虑翼伞上述优化目标和控制约束，翼伞的最优控制航迹规划问题可用如下数学形式描述：

1) 翼伞空投初始条件

x(t0)=x0,y(t0)=y0,h(t0)=h0,ψ(t0)=ψ0

(2)

式中：t0为空投初始时刻；x0、y0、h0为初始时刻位置；ψ0为初始时刻航向角。

2) 翼伞着陆时刻终端约束条件

x(tf)=xf,y(tf)=yf,h(tf)=hf,ψ(tf)=ψf

(3)

式中：tf为着陆时刻；ψf为着陆目标点风向的反方向角度，不失一般性，可假定着陆点风向与x轴正向一致，即ψ(tf)=180°，或ψ(tf)=-180°，则逆风着陆条件可转化为cos(ψ(tf))=-1，此时若快速下拉翼伞两侧操纵绳，可实现翼伞的逆风雀降。

3) 避障约束

在战场环境或复杂地形条件下，翼伞空投区域可能存在敌方火力或山峰障碍，因此规划航迹需绕过这些障碍。不失一般性，本文将山峰障碍和敌方火力等威胁统一建模为山峰障碍，即

h(x,y)=

(4)

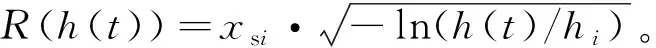
4) 控制约束条件

|u|≤umax

(5)

由于翼伞操纵绳的绳长有上限，导致控制量有上限值，当翼伞操纵绳的下拉量达到上限值时，翼伞转弯半径为最小值。

5) 优化目标函数

规划航迹的优劣需要采用目标函数来衡量，前述距目标点最近、逆风着陆、控制能耗最小、避障等优化目标，可用如下目标函数表示：

J1=min[(x(tf)-xf)2+(y(tf)-yf)2]

(6)

J2=min(cos(ψ(tf))+1)

(7)

(8)

为实现对山峰障碍的规避，需首先计算翼伞到山峰表面距离与设定安全距离的误差：

(9)

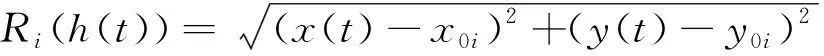
(10)

该值越小说明翼伞碰撞到山峰的可能性越小。

上述目标需要平衡兼顾，可采取加权的方式，将上述多目标函数转化为单目标函数：

J=f1J1+f2J2+f3J3+J4

(11)

式中：f1、f2和f3为加权因子，可根据不同任务的不同侧重点，选择不同的取值。

3 基于梯度下降的最优分段航迹规划

根据翼伞归航任务的要求，翼伞系统最优控制航迹规划问题可归纳为：在翼伞系统方程(1)的约束下，设计满足控制约束条件(5)的最优控制律u*，使系统状态从初始条件(2)转移到终端条件(3)，同时使得目标函数(11)为最小值。用数学表达式描述如下：

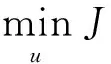
(12)

本节将控制变量分段常值化，以求解问题(12)，首先将时间段[t0,tf]分为n个相邻区间序列，在每个子区间内u取常数值以控制翼伞系统，如图1所示。

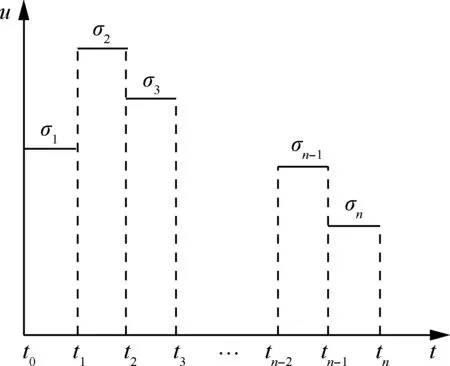
图1 分段常值控制Fig.1 Segment constant control

则翼伞的控制量可用分段常值序列函数近似表示：

(13)

其中:

(14)

控制变量离散化后，问题(12)即变成了经典的控制参数优化选择问题，可以用随机搜索，也可以用目标函数对控制变量的梯度求最优控制量，随机搜索比较耗费时间，而梯度下降法耗时较短，因此本文采用梯度下降法，快速获得最优控制序列。

梯度下降法又名最速下降法，函数J(u(t))在某u(t)取值处的梯度方向，是J下降最快的方向，梯度下降法理论简单，编程较容易实现。在求目标函数的最小值时，从定义域内任意初始点出发，沿着负梯度方向可以最快到达极小值点，定义J对u的负梯度方向为

(15)

式中：du是控制变量的变化量，也称为控制量步长。利用式(15)可得控制量序列的迭代公式为

ul+1(t)=ul(t)+λSl

(16)

式中：ul+1(t)和ul(t)分别为第l+1代和第l代控制量，λ为学习率，λ的取值较为关键，如果其值取的过大，梯度下降算法可能会发散，如果其值取的过小，则控制量的更新收敛速度慢，算法需要花费更多的时间才能得到最优值。下面为梯度法求解翼伞最优归航轨迹的具体算法：

1) 随机给定控制量常值序列初始值u0(t)，学习率λ，分段值n，控制量步长du(t)，分段常值的上界和下界，迭代次数最大值等，容许误差e，同时令l=0。

2) 将控制量ul+1(t)和ul(t)分别代入式(1)，利用初始条件(2)、终端条件(3)，计算性能指标J(ul+1(t))和J(ul(t))，再通过控制量步长du，计算负梯度

3) 检查迭代次数是不是达到最大，若是则跳转到步骤6)，否则继续。

4) 更新控制量ul+1(t)：ul+1(t)=ul(t)+λSl，如果ul+1(t)≥umax，则取ul+1(t)=umax；如果ul+1(t)≤-umax，则取ul+1(t)=-umax。

5)l=l+1，转步骤2)。

6) 若迭代次数达到最大值，或性能指标函数变化量小于e，输出最优控制序列u*(t)。

4 算法仿真分析

为验证本文所设计航迹规划算法的有效性，本文分别在无障碍和存在山峰障碍情况下对提出的航迹规划算法进行了仿真。

1) 无障碍情况下的航迹规划

本文为了分析所提出的航迹规划算法特点，在无障碍情形下对比了本文算法、基于高斯伪谱法的最优控制归航算法和基于遗传算法的分段归航算法，其中伪谱最优航迹算法参考了文献[4-5]等，分段航迹算法参考了文献[13, 15-16, 20]等。图2为三者的对比曲线，其中蓝色点划线为基于遗传算法的分段航迹规划算法相关曲线，黑色虚线为基于高斯伪谱法的最优控制航迹规划算法相关曲线，红色实线为本文提出的最优分段航迹规划算法相关曲线。

翼伞空投初始点位置设为(1 500，1 000，2 000)m，翼伞的速度设为v=10 m/s，初始航向角设为45°，水平速度vs=9.5 m/s，vz=3.1 m/s，滑翔比约为3.1，umax=0.18。本文将常值风的影响视为空投初始位置偏移，u(t)的分段值n设为6，du(t)=0.002，学习率λ设为0.01，迭代最大次数设为6 000次，目标函数系数f1、f2和f3分别设为0.01、16、4，此时不考虑避障指标J4，得到的航迹规划结果如图2所示。

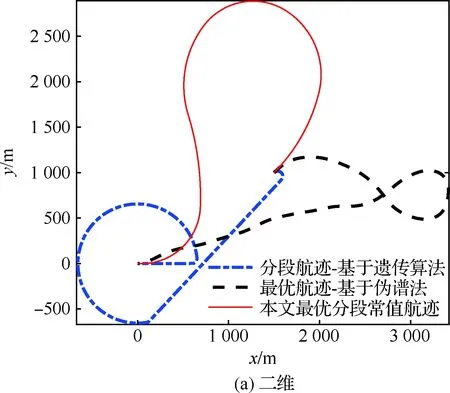
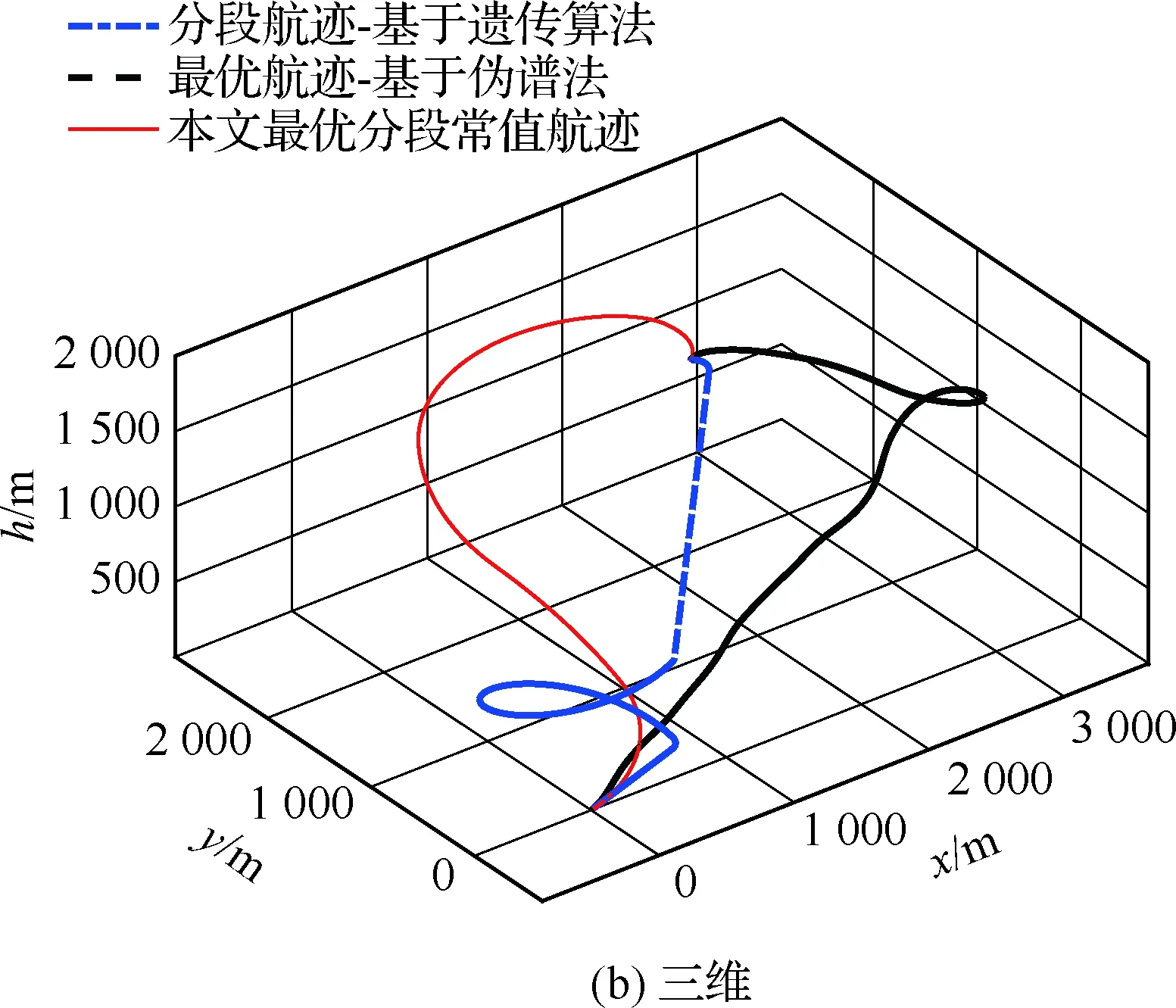
图2 无障碍情况下的规划航迹对比Fig.2 Comparison of planned trajectories without obstacles

从图2的归航轨迹可以看到，基于遗传算法的分段航迹算法、基于高斯伪谱法的最优控制航迹算法，以及本文基于梯度下降法的最优分段常值航迹算法，都可以有效地为翼伞系统规划出可行航迹，三者从同一初始点出发，经过不同航迹都能到达同一个目标点，同时还满足逆风精确着陆的要求。在分段归航航迹中，翼伞经过目标接近段、能量控制段和逆风着陆段到达了目标点；在高斯伪谱法最优航迹中，翼伞先向远端飞行，消耗掉一定高度后再转向目标点飞行；而在本文设计航迹中，翼伞通过一个较大半径的迂回转弯消耗高度再着陆到目标点，规划的目标点位置为(0.099 0，0.254 2) m，实现了精确归航。

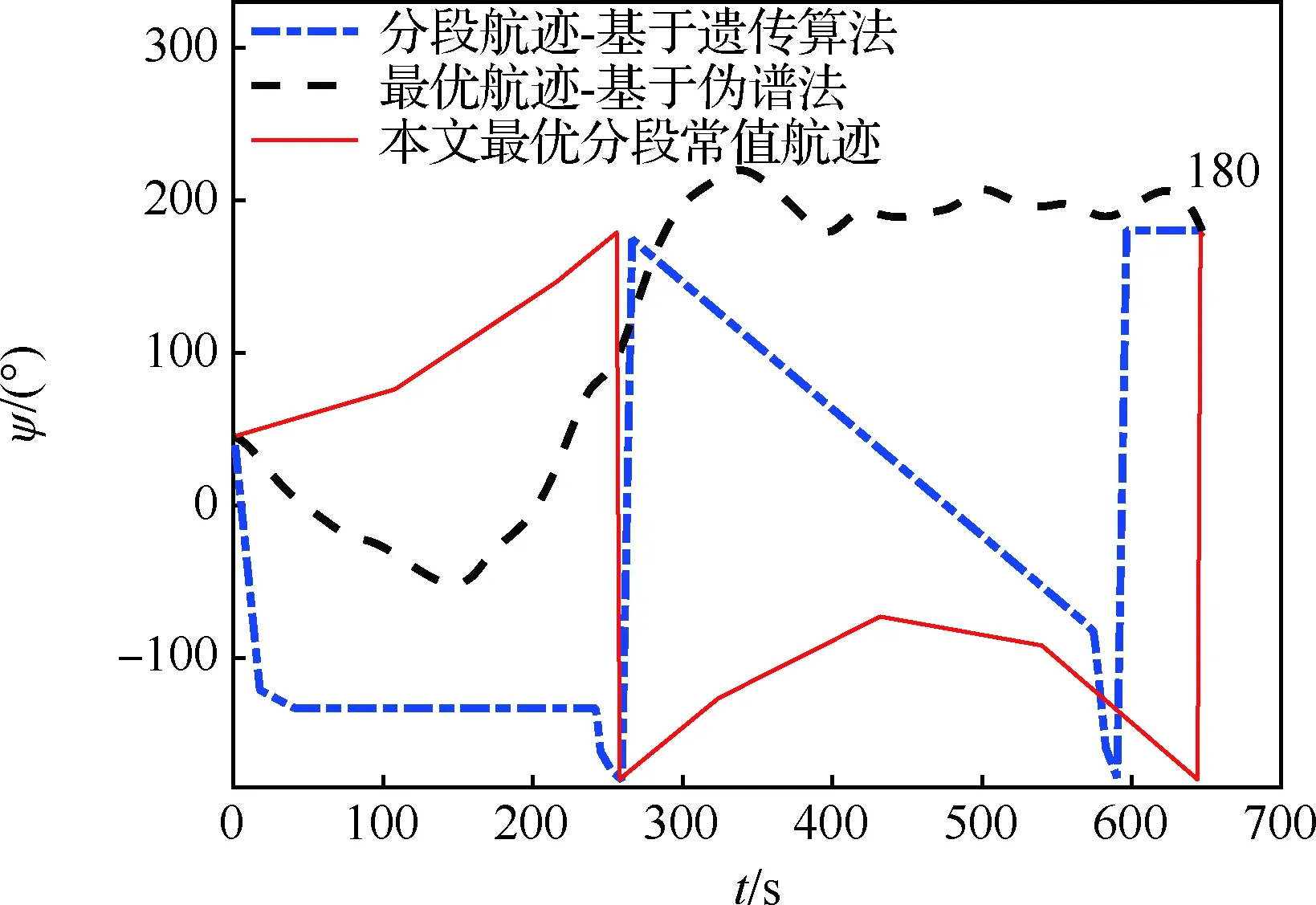
图3 无障碍情况下规划航迹的航向角对比Fig.3 Comparison of heading angles of planned trajectories without obstacles

从图3航向角对比图可以看到，从相同45°初始航向角出发，分段归航、最优归航和本文归航算法在着陆时的航向角基本上都在180°左右，实现了以180°角逆风着陆的目标。

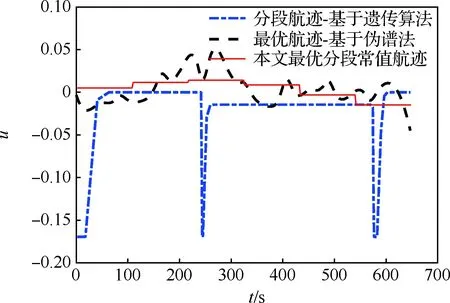
图4 无障碍情况下控制量的对比Fig.4 Comparison of control quantities without obstacles

从图4控制量的变化曲线可以看到，3种航迹规划算法下翼伞的控制量都小于允许的最大值，规划的航迹满足翼伞控制特性，是可飞的。其中最优控制归航着陆精度高、控制量小，但控制过程是连续变化的曲线，控制电机需要连续不断调整才可以实现控制目标，控制难度较大；而分段归航的控制量为分段常值，主要涉及转弯、滑翔、雀降等几个简单操作，其控制操作比最优归航要简单，从工程实用性角度出发，分段归航方式比最优控制归航方式更容易实现，但可以发现分段归航控制量较大，此外在初始方向调整段、目标接近段到能量管理段之间的过渡段、从能量管理段到逆风着陆段之间的过渡段，翼伞都需要从一个较小控制量突然增大到最大控制量，然后又从最大控制量降低到较小控制量，这增加了操纵的难度，同时由于翼伞控制存在较大的滞后，当控制还没有完全起作用时，很快又将控制量从最大控制量降低到较小控制量，这种操作将会带来较大的跟踪误差。跟前两种航迹规划算法相比，本文设计的航迹规划算法结合了最优控制航迹规划和分段航迹规划算法的优点，首先，跟前两者一样，规划的航迹着陆精度高，实现了精确着陆；其次，控制能量消耗较小；再次，控制是分段常值，操纵容易；最后，从图4中可以看到，本文算法设计的控制量主要在基准值附近变化，且其变化不大，这为后续的航迹跟踪提供了更大的控制量冗余。

2) 存在山峰障碍情况下的航迹规划

考虑存在3座山峰，其中心分别坐落于坐标(2 000,1 000) m、(1 000,3 000) m、(400,1 500) m处，山峰高度分别为2 500、2 000、1 800 m，坡度相关量xsi分别为550、480、380 m，设定的安全间距Rsafe为50 m，其余空投条件跟无障碍情形完全相同。考虑到分段归航法没有避障能力，但伪谱法有避障规划能力，因此本文还对基于伪谱法的最优避障和本文提出的最优分段常值避障规划效果进行了对比，如图5所示，其中黑色曲线为伪谱法避障规划航迹，红色曲线为不考虑避障时的最优分段归航航迹，蓝色曲线为考虑避障时的最优分段归航航迹。

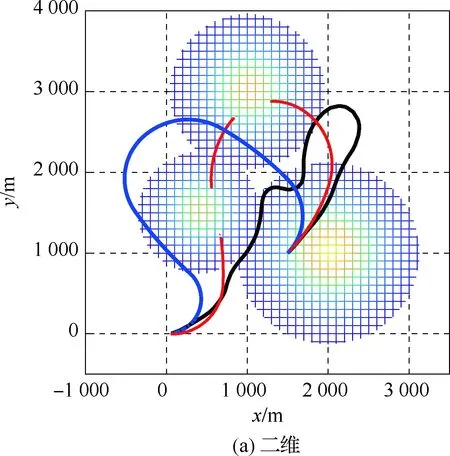
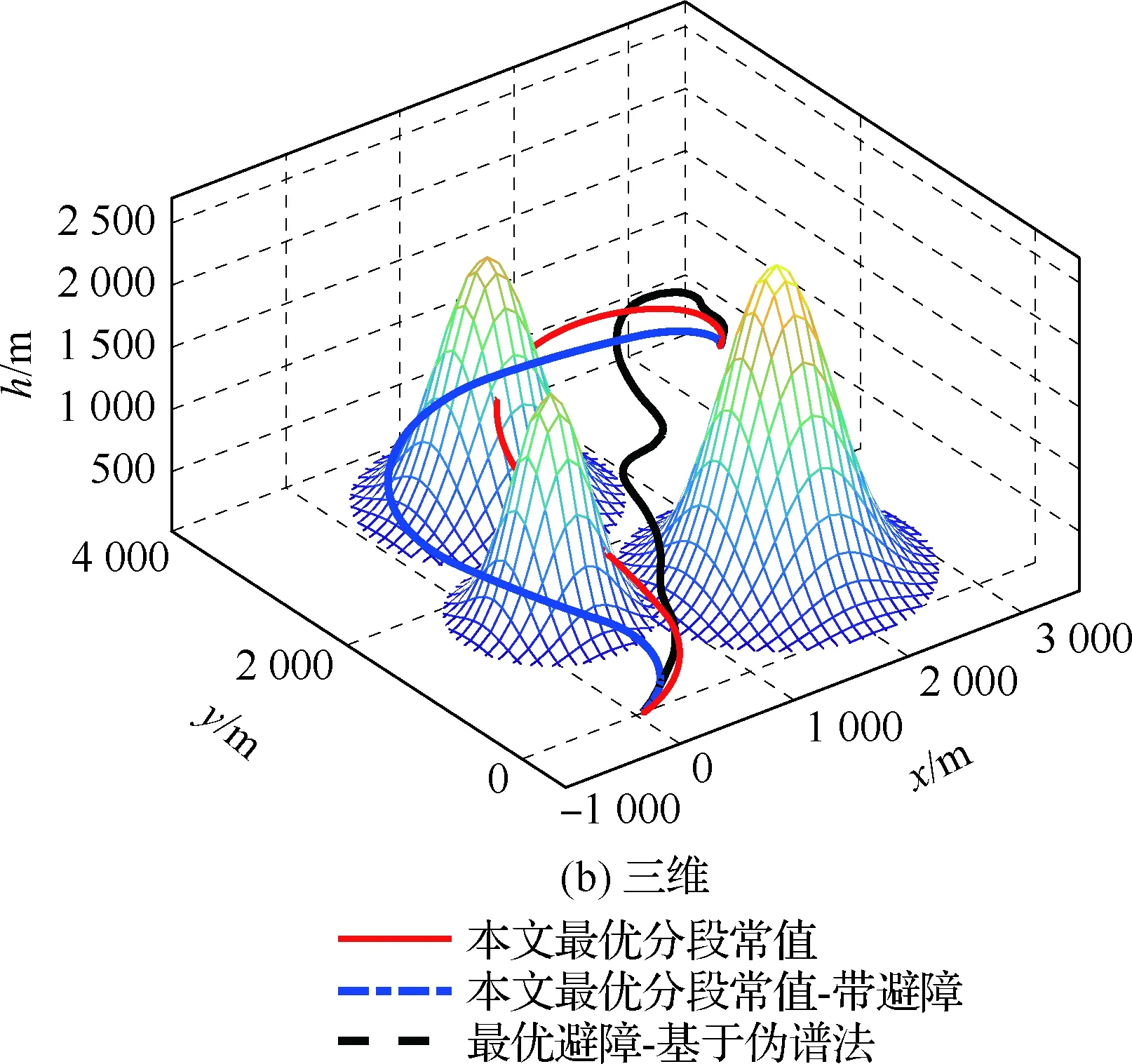
图5 有障碍情况下规划航迹对比Fig.5 Comparison of planned trajectories with obstacles

从图5中可以看到，在不考虑避障指标J4时，本文提出的最优分段常值规划航迹将穿山而过，若翼伞系统跟踪该航迹，则势必会撞上山峰障碍，但在引入避障指标后，本文提出的最优分段常值避障规划航迹绕过了山峰障碍，逆风精确着陆到目标点。此外还可以看到伪谱法也能实现对山峰的避障规划，并逆风精确着陆到目标点，说明伪谱法同样是一种优秀的航迹规划算法。

从图6可以看到，在考虑避障后，本文提出的最优分段避障航迹规划算法可以实现逆风着陆，不过其最终着陆角度为-180°，但-180°和180°在方向上是重合的，同属于逆风方向。

图7为本文提出算法和伪谱法算法控制量的对比，可以看到在有障碍的情况下，本文提出算法获得的控制量为分段常值，变化依然较小。

表1进一步给出了几种航迹规划算法的规划指标结果对比，从表中数据可以看到，分段归航只要求控制量在约束范围内即可，因此分段归航航迹跟最优归航航迹相比，分段归航能量消耗较大；最优控制航迹规划算法在着陆距离偏差和逆风着陆方面的表现最好，且最优归航控制的能量消耗总值要比分段归航小一个数量级，这是由于最优控制归航将控制量能量最小作为目标函数设计指标之一；而本文提出的最优分段常值归航算法在距离偏差和逆风着陆方面有所折衷，但能量消耗最小，从目标总值看，本文提出的算法目标函数总值是最低的。

此外可以看到，在存在障碍的情况下，本文提出算法和伪谱法两者的能量消耗都比无障碍情况下要高，同时还可以看到伪谱法的着陆精度误差和逆风角度误差都为0，精度极高，但付出的代价就是翼伞需要连续不断的调整控制量。

图8为本文提出算法的目标函数随迭代次数的变化情况，在CPU配置为i5-5250、内存配置为8 G 的2015版Macbook Air笔记本电脑上，当不考虑避障时，本文航迹规划算法在迭代次数为1 200 左右时就已完全收敛，算法运行时间为4.79 s；当考虑避障时，迭代次数为2 200时算法收敛，算法运行时间为45.18 s，此时运行时间稍长，但也不足一分钟。此外，两种情形下梯度下降法的目标函数最小值分别为0.309 2和0.452 8。

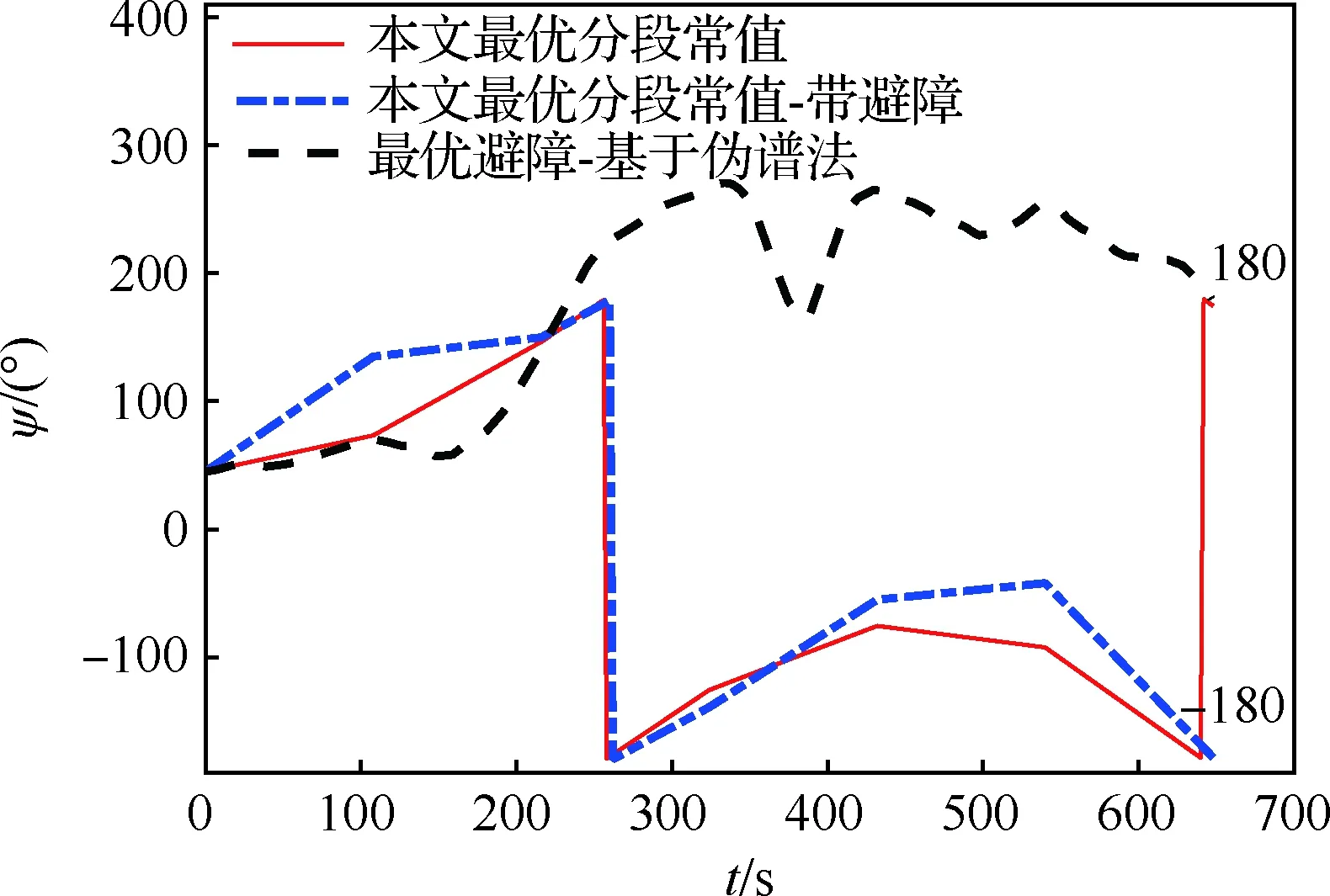
图6 有障碍情况下规划航迹航向角的对比Fig.6 Comparison of heading angles of planned trajectories with obstacles

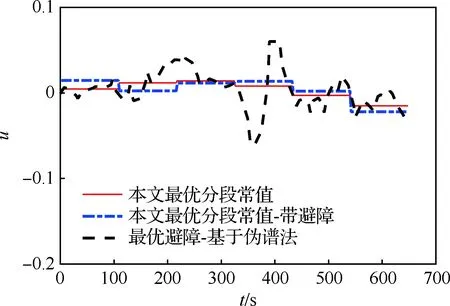
图7 有障碍情况下控制量的对比Fig.7 Comparison of control quantities with obstacles

表1 航迹规划算法指标结果对比Table 1 Trajectory planning algorithm indexes

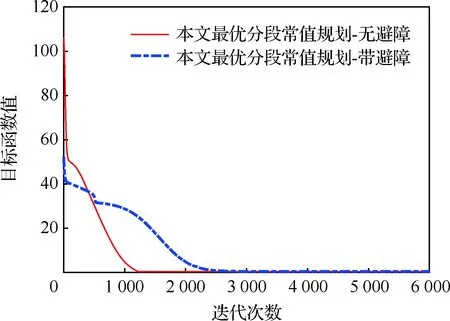
图8 目标函数值随迭代次数的变化曲线Fig.8 Curves of objective function with number of iterations

5 结 论

本文提出了一种基于梯度下降法的航迹规划算法，提出的算法综合了传统分段法和最优控制法的优点，规划的航迹综合考虑了着陆精度高、控制能量小、逆风着陆、避障等最优目标；同时规划航迹由简单的分段航迹组成，使得控制操作较为简单；此外，在整个飞行过程中翼伞控制量的值都比较小，控制量不需要像分段归航法那样忽大忽小的变化，也不需要像最优控制伪谱法那样连续变化，因此在提供较大控制量冗余的同时，简化了控制操作。本文算法为翼伞系统航迹规划研究提供了新的思路。