基于增强型离散相模型和化学燃烧的红外诱饵弹建模方法
2020-12-29杨春玲张振东张潼奕聿
杨春玲,张振东,张潼奕聿
哈尔滨工业大学 电气工程及自动化学院,哈尔滨 150001
红外诱饵弹是一种使用率很高的红外对抗武器。问世至今,它凭借成熟、可靠及价格低廉等优点,被各军事大国广泛应用于实战[1-2]。当红外目标被锁定时,会发射红外诱饵弹来诱骗进攻武器,达到保护自身的目的。因此,建立一种准确的红外诱饵弹仿真模型,无论是针对红外制导算法的抗干扰性研究还是红外诱饵弹的诱骗效果研究,都将具有重大的意义。
目前针对红外诱饵弹的主流建模方法有基于纹理特征的、基于仿真粒子算法的和基于计算机流体仿真(Computational Fluid Dynamics,CFD)的红外诱饵弹建模法等。
基于纹理特征的建模方法[3-5]是一种相对较为传统的方法,它的原理是先通过观测和总结火焰、烟幕等对象的条纹信息,再利用数理统计的方法建立出相应的经验模型。由于这种方法属于早期的经验公式建模法,缺少机理性的研究,因此在计算机运算能力明显提升后很快就被其他数值方法取代了。
基于仿真粒子算法的红外诱饵弹建模方法[6-7]思想如下:首先,假设红外诱饵弹是由空间中初始位置随机分布的大量红外辐射粒子构成的;然后,以每一个粒子为研究对象,通过施加大小和方向都随机的力驱动粒子做布朗运动;接下来,根据仿真要求添加“仿真风”,使粒子具有某些一致性的运动规律;最后,通过添加这两种因素仿真得到每个颗粒的运动轨迹,进而仿真得到红外诱饵弹的模型。这种方法属于统计学建模方法,它运算量较小且生成图像速度较快,目前在很多半实物仿真平台上有广泛应用[8]。然而,这种方法缺乏机理性研究,也并没有过多地研究红外诱饵弹辐射特征的产生机理。
随着计算机运算能力的不断增强,基于CFD的红外诱饵弹仿真方法[9-10]凭借其仿真精度高、机理性研究能力强的优点,已逐渐成为主流研究方法。而基于CFD的仿真方法主要有连续相建模和离散相建模两种方法。
其中,连续相建模方法将红外诱饵弹喷射的物质简化为热气流或可参加化学反应的气体物质(如CO),然后求解Navier-Stokes(N-S)方程,建立湍流模型,计算得到诱饵弹的辐射特征。这两种连续相的假设中,简化为热气流计算较为容易,但由于气体比热容较小,因此换热速度较快,模型辐射特征持续时间较短;而简化为可参加化学反应的气体物质尽管可以通过燃烧获得化学能量补偿,保持更长的辐射时间,但这种仿真方法将化学反应简化为均相反应,不符合化学反应动力学过程,因此其辐射光谱准确性较差。
相较连续相建模方法,离散相建模方法是近些年发展起来的一种新型建模手段。它首先以颗粒为研究目标,通过建立Lagrange坐标系分析流场中颗粒的受力情况,计算分子的运动轨迹;然后借助计算机仿真能力,通过追踪大量颗粒建立宏观物体的运动、辐射等模型。
离散相模型对于由大量颗粒(如煤、沙尘等)组成的宏观现象研究效果较好,而红外诱饵弹也有着上述相同的特征,它是一种由药剂颗粒运动和燃烧产生辐射特征的红外目标。因此,离散相建模方法将更加贴近真实物理过程,具有更高的建模精度。张振东等[11-12]建立了一种基于离散相模型(Discrete Phase Model,DPM)的红外诱饵弹辐射特征模型,首先以颗粒作为研究对象,通过求解力学平衡方程和N-S方程计算每个颗粒的受力情况和运动轨迹;然后加入离散坐标(Discrete Ordinates,DO)辐射模型建立红外诱饵弹的辐射特征模型。在此基础上,张振东等[13]又建立了增强型的DPM模型,通过编写用户自定义编程文件(User Define Files,UDF)的方法引入了多种附加力,建立了复合颗粒喷口,并利用扩展型“等效黑体分子”辐射模型建立了红外诱饵弹的辐射特征模型。
虽然这种离散相模型确实具有较高的仿真精度,但以上研究[11-13]并没有考虑颗粒燃烧对红外诱饵弹辐射特征产生的影响。而通过分析红外诱饵弹的工作机理[14-18]可以发现,诱饵弹的辐射特征主要由两部分构成:① 由氮氧化合物和碳氧化合物构成的高温气体;② 由燃烧的红外诱饵药剂(如Mg、聚四氟乙烯(PTFE)和Viton混合物(MTV)材料)构成的高温颗粒。由此可见,仅以气体相或仅以固体相建模,而不考虑化学燃烧对红外诱饵弹的影响,得到的结论无疑会在一定程度上存在误差。
综上,本文将针对化学组分燃烧对辐射特征产生的影响做进一步研究。首先,建立一种层流场中的MTV燃烧数值仿真模型,该模型以MTV颗粒为研究对象,通过分别求解流体力学基本方程组和化学组分守恒定律,先计算MTV颗粒的空间运动轨迹、与周围环境在质量和能量上的交换情况,再引入增强型DPM模型,计算得到颗粒的运动状态,并借助CFD仿真软件计算不同时刻的MTV颗粒燃烧时的物理状态;然后,建立扩展型“等效分子黑体”模型,计算红外诱饵弹的辐射特征;最后,设计实验进行验证。
1 数学模型
实战中,红外诱饵弹会喷射大量燃烧颗粒在作战空域形成红外干扰。因此在理论研究红外诱饵弹的数学模型时,需要分别从气体相、固体离散相和化学燃烧相的角度进行建模研究。
1.1 气体相的控制方程
建立层流低马赫数下的气相模型,其质量守恒定律、化学组分守恒定律、动量守恒定律和能量守恒定律可以变形为
(1)
(2)
(3)
(4)
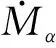
(5)
(6)
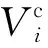
假定统一Lewis数,化学组分的扩散系数可以根据热系数计算得到。基于Stokes假说的牛顿流体假设,黏性张力可以通过计算得到:
(7)
式中:μg为混合气体的动态速度;U为流体速度。
气体相均匀反应释放的热量可以通过式(8)计算得到:
(8)
式中:hα为第α相的反应焓变量。
理想气体的状态方程用于使方程组收敛。组分传输系数、反应速率和混合物的热力学关系可以通过Blanquart等[19]、Cai和Pitsch[20]提出的方法计算得到。
1.2 固体相的控制方程
对于固体相而言,能量方程可以通过式(9)进行求解:
(9)
式中:ρs、cp,s、Ts和λs分别为固体相的密度、定压比热、温度和导热系数。混合物中,Mg作为分散相球形颗粒散布在PTFE连续相基体中。二元混合物等效导热系数λs可以通过Maxwell模型计算得到:
(10)
式中:λm为PTFE的导热系数,λm=0.244 W·m-1·K-1;λd为Mg的导热系数,λd=156 W·m-1·K-1;Vd为Mg的体积分数。
MTV颗粒的密度主要取决于MTV颗粒在高温情况下的挥发速率和颗粒表面的氧气分布程度。MTV烟火剂的密度为1.79 g/cm3,Mg、PTFE和Vtion的质量分数分别为60wt%、35wt%和5wt%。
1.3 DPM模型的数学模型
DPM模型是通过对Lagrangian参考系下颗粒的运动方程求积分计算运动轨迹的。考虑颗粒的惯性与受力平衡,分散相粒子运动方程(以直角坐标系内x方向为例)为
(11)
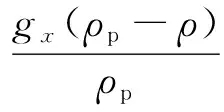
(12)
(13)
(14)
式中:μ为连续相黏度;CD为颗粒的比热容;Re为雷诺数;dp为颗粒直径;a1和a2为系数,a1=0.364 4,a2=98.33。
在固体相中,质量传输和组分传输被忽略了。因此,对于固体相而言,只需通过式(9)计算它的能量方程。
1.4 气-固交界面处的控制方程
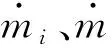
根据组分、质量和能量源与气体和固体通量之间的平衡,可以得到组分、质量和能量交界面方程为
(15)
(16)
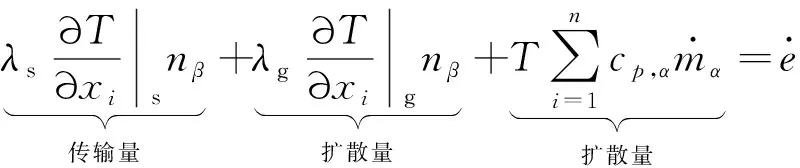
(17)
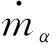
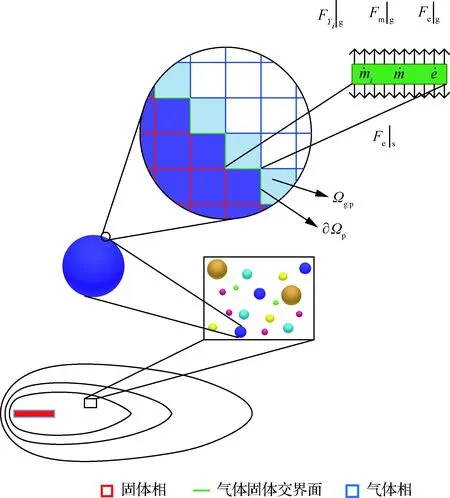
图1 化学反应时组分微观变化示意图Fig.1 Schematic diagram of microscopic changes of components in chemical reactions
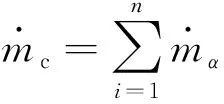
(18)
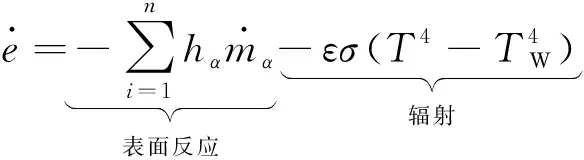
(19)
式中:ε为发射率,ε=0.73;σ为Stefan-Boltzmann常数;TW为壁面温度。
固体相表面非均相反应决定的每一组分的产生和消失速率可以通过如式(20)和式(21)所示的化学反应进行计算。由于交界面处的非均匀性反应,Waite等[21]提出了一种用于计算每一项产生和消耗速率的化学反应机理:
(m-2n)Mg(g)+nC(s)+qan
(20)
2CO2+qae
(21)
式中:qan为厌氧环境中化学反应焓;qae为空气中化学反应焓。
化学组分在燃烧时的燃烧特性如文献[15-17]所示,红外烟幕的光照强度Lλ(W·sr-1·cm-2)由化学组分的消耗速率∂m/∂t(g·s-1·cm-2)和光谱效率Eλ(J·g-1·sr-1)共同决定,他们之间的数值关系为
Lλ=Eλ∂m/∂t
(22)
光谱效率Eλ与整体化学反应的焓变(ΔrH=qan+qae)、发射率ε和化学反应生成物的温度之间的数值关系为
Eλ=(4π)-1ΔrHF(λ,T)
(23)
式中:F(λ,T)为不同温度下光谱辐射率,可根据普朗克公式计算;λ为光的波长。
Koch等[22-25]给出了MTV烟火剂中各组分的物理特性和化学特性,如表1所示。
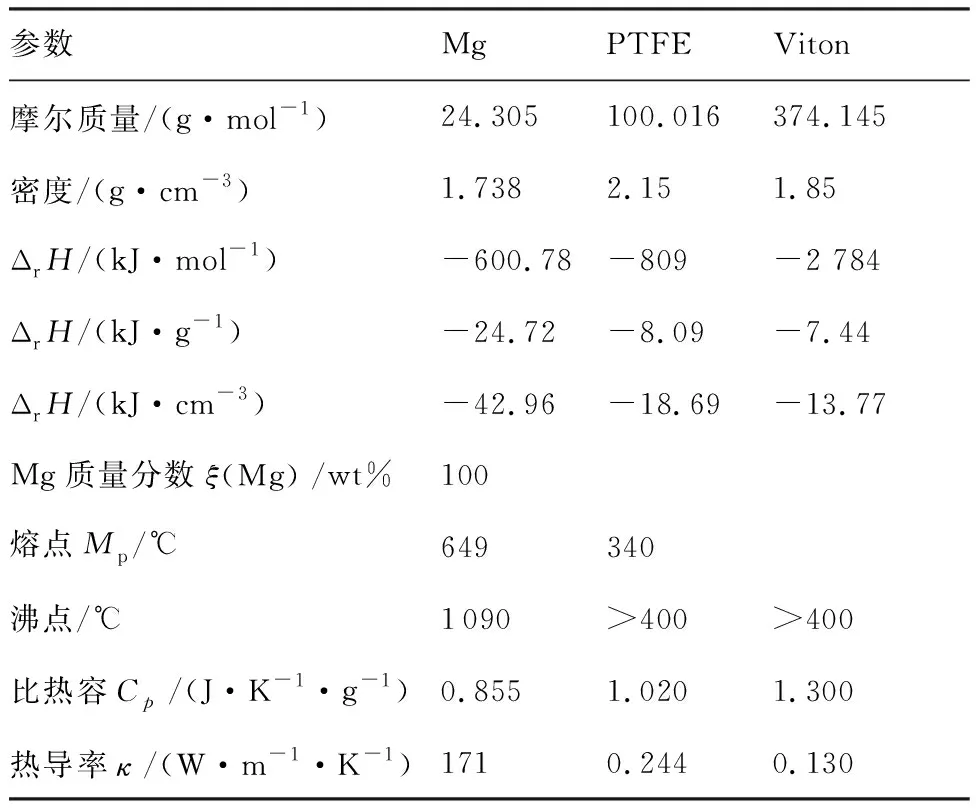
表1 MTV烟火剂中各组分的物理特性[22-25]
2 基于动态计算网格的红外诱饵弹仿真模型
在分别从气体相、固体离散相和化学燃烧时的气固耦合等方面对红外诱饵弹进行理论建模后,进一步建立动计算网格研究红外诱饵弹在旋转时的红外特征。
2.1 “复合颗粒喷口”边界条件设计
在连续相入口处,流场的速度和湍流强度等边界条件被分别设置为常数。由于离散相的空间分布存在明显的随机性,通过编写用户自定义函数(UDF)设计了复合颗粒边界条件。复合颗粒喷口边界条件是将颗粒按照直径分成n组,并保证每一组的颗粒均满足高斯分布。因此,当n的数值很大时,数值模型就将能够更加准确地模拟实验模型。为了计算方便,令n′=6,直径分别为0.50、0.75、1.00、1.25、1.50、1.75 mm,每一组均占颗粒总量的16.7%,喷口的截面图如图2所示。
在出口和远场处,为防止由气压差造成的空气回流,出口设置为数值是1 atm的压力出口。同时,当颗粒经过出口处后,颗粒将会被从计算域中删除。
弹体表面的壁面条件选择无滑移标准壁面函数,同时假设当颗粒碰撞弹体时会产生反弹。为研究标准壁面函数中颗粒反弹因子对仿真结果的影响,分别设计了反弹参数为0.5、0.7和1.0的3个实验,结果如图3所示。结果表明,反弹因子对颗粒在弹体表面处的分布影响并不明显,因此反弹参数选择1.0。
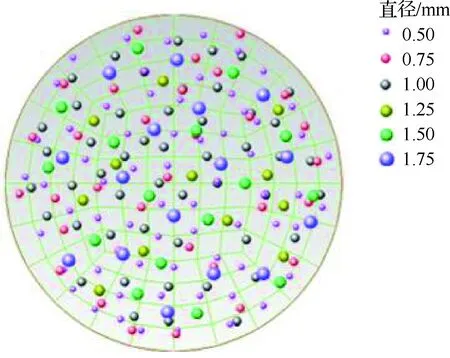
图2 喷口处个质量颗粒空间分布示意图Fig.2 Spatial distribution diagram of mass particles at nozzle
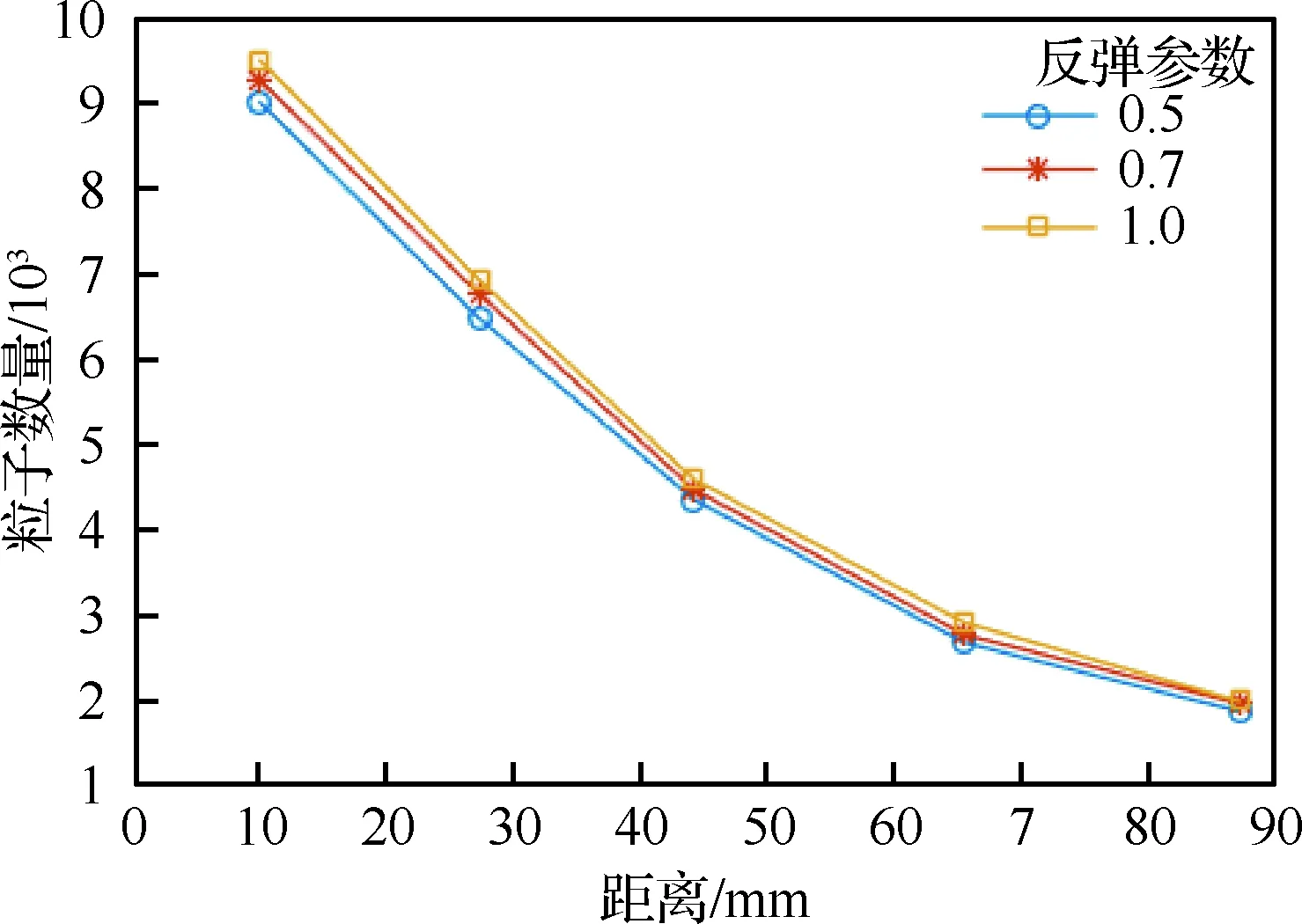
图3 壁面反弹因素对颗粒空间部分的影响Fig.3 Influence of wall rebound on spatial part of particles
2.2 动网格计算域划分
在借助有限元仿真工具对增强型DPM模型的数值模型进行仿真验证时,需要根据研究对象的结构特征和运动特征等设计适当的流场计算网格。由于建立的模型考虑了弹体多自由度运动对仿真结果的影响,因此设计了一种基于动态网格的流场计算网格。大量仿真实验表明,动态网格的网格形式、参数和结构等因素将直接影响仿真的时间长度和最终的仿真结果。所以,在设计多组对比实验后,最终建立了一套恰当的流场计算网格。
图4(a)为“∏P∏-50”红外诱饵弹的弹体结构。可以看出,喷口平均分布在弹体的表面,使红外诱饵弹的弹体表面呈现一种“玉米棒”形。根据这种弹体结构模型建立如图4(b)所示的3D模型。
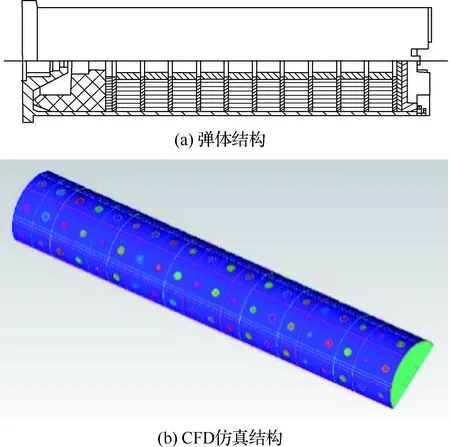
图4 红外诱饵弹结构Fig.4 Structure of infrared decoy bomb
由于实战中诱饵弹出膛瞬间附带的切向力会导致弹体旋转,从而影响整个红外诱饵弹在空间中的分布。因此,为了能够仿真诱饵弹旋转时红外诱饵弹的空间分布和物理特征,将流场分割为如图5所示的形式,即靠近弹体的流场区域被设计为半球形,其近场网格均为结构化网格,如图5(b)所示;远场部分的网格同样是由尺寸更大的结构化网格构成,如图5(c)所示。
在将流场整体划分为远近两个子计算域后,下一步即分别研究它们的网格形式和网格数量等参数的划分方案。在设计网格时常常需要面对一些两难的选择,例如:尽管网格数量的增加可以使仿真结果更加接近真实结果,却会带来计算时间成倍增长的问题;结构化网格虽然会使计算时间缩短,使计算结果呈现更好的收敛性,但同时也为网格设计工作带来很大的不便。
针对这些网格参数的选择设计了对比实验,计算网格参数选择对比试验结果如表2所示。对比实验的判断依据综合考虑了网格质量和尾焰仿真结果温度变化率。其中,计算温度变化率的方法是首先计算相同弹体和流场尺寸时,使用结构化静态网格仿真得到的最高温度T0,然后分别计算各个网格划分方案中仿真结果的温度Tn′,最后计算1-(Tn′/T0)。
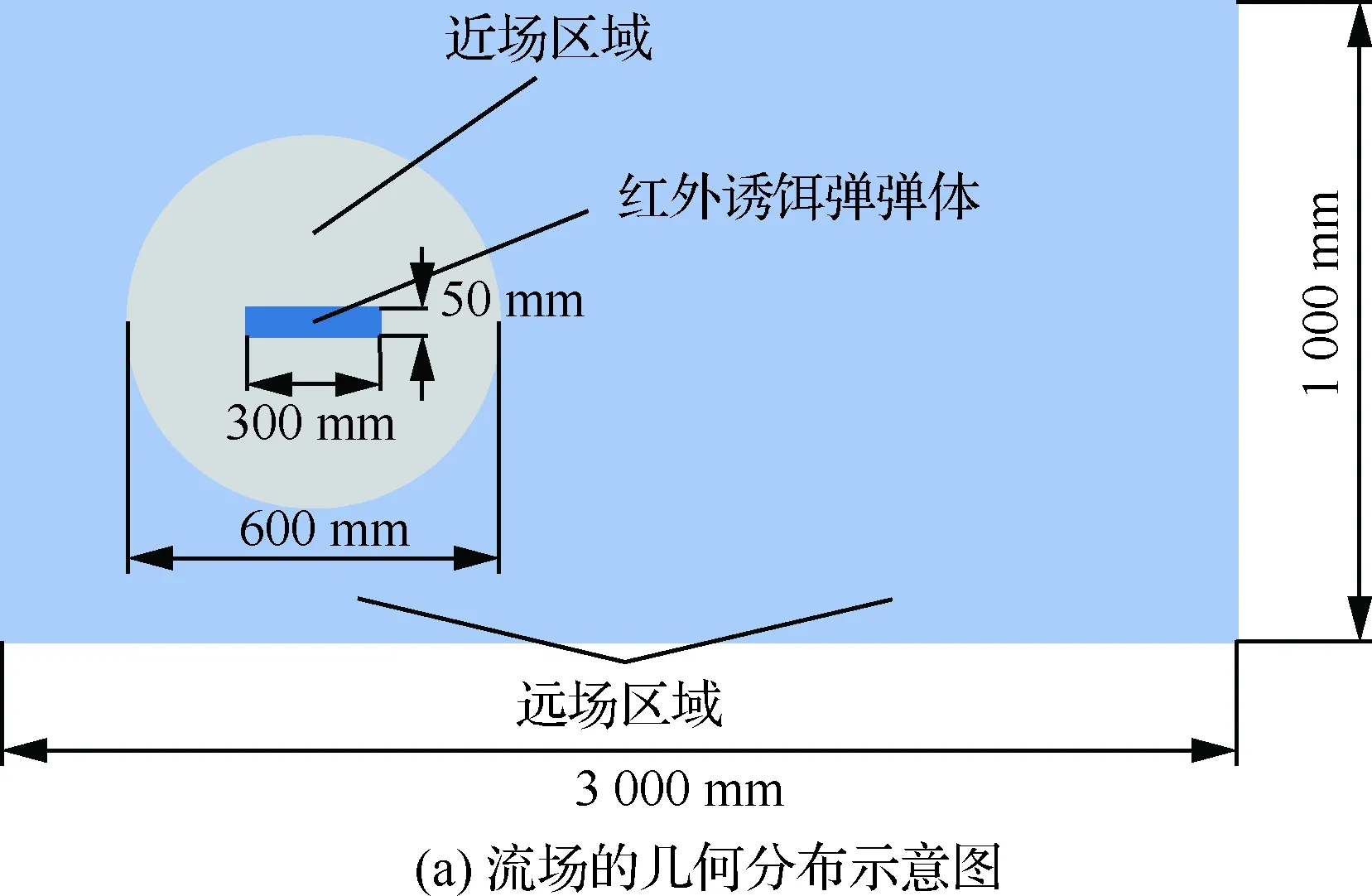
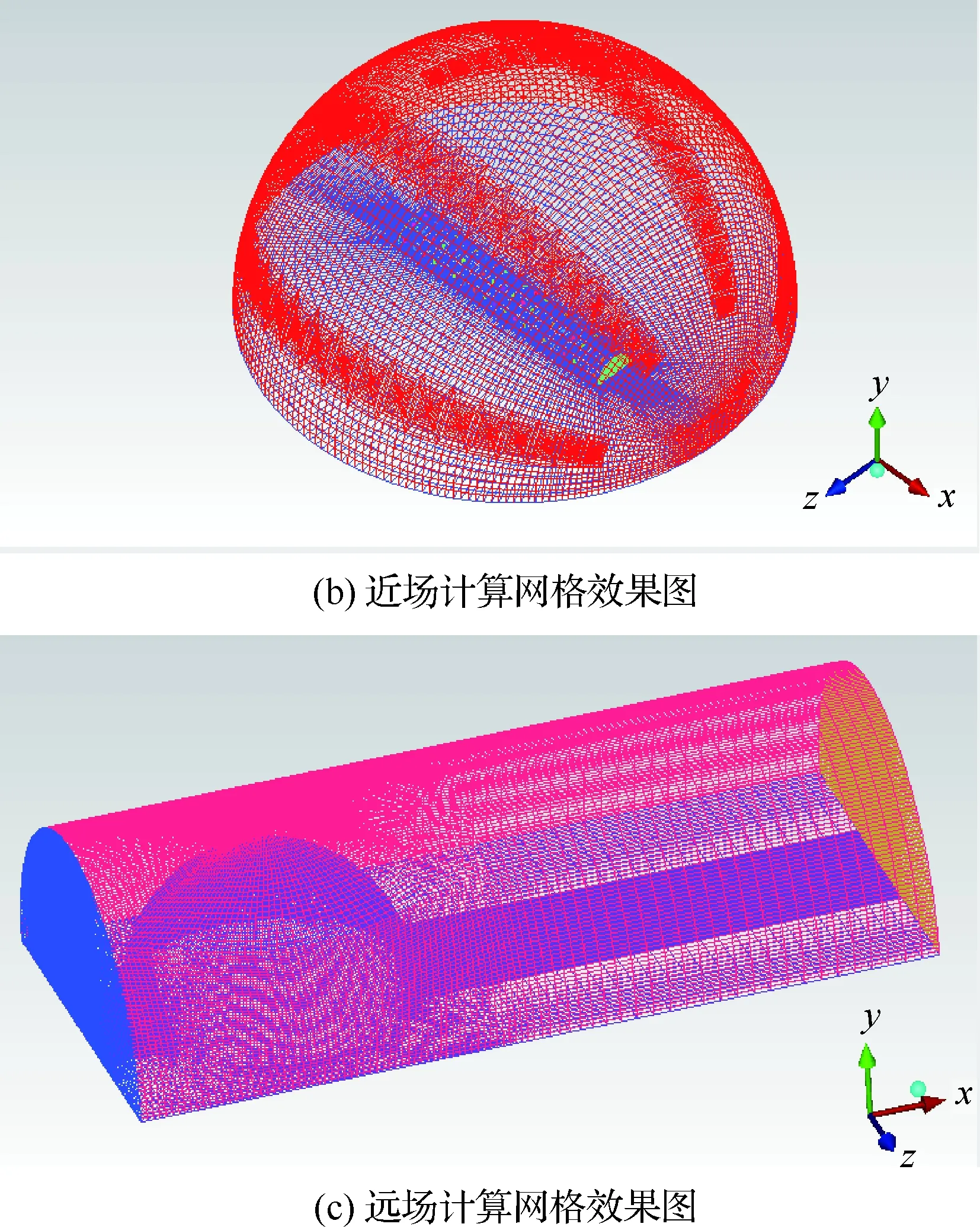
图5 流场的空间分布和计算网格Fig.5 Spatial distribution of flow field and computational mesh
2.3 数值仿真结果及分析
在确定网格形式和网格参数后,使用该计算网格进行数值仿真,分别得到了弹体的组分分布图和弹体旋转时的温度云图,如图6和图7所示。
从图6中可以看出组分分布具有如下共同特点:MTV药剂刚被喷射出来时,C含量和Mg蒸汽含量比较高;高浓度MTV药剂的剧烈化学反应迅速消耗了氧气,在弹体近处形成厌氧区;此时的化学反应过程如式(20)所示。
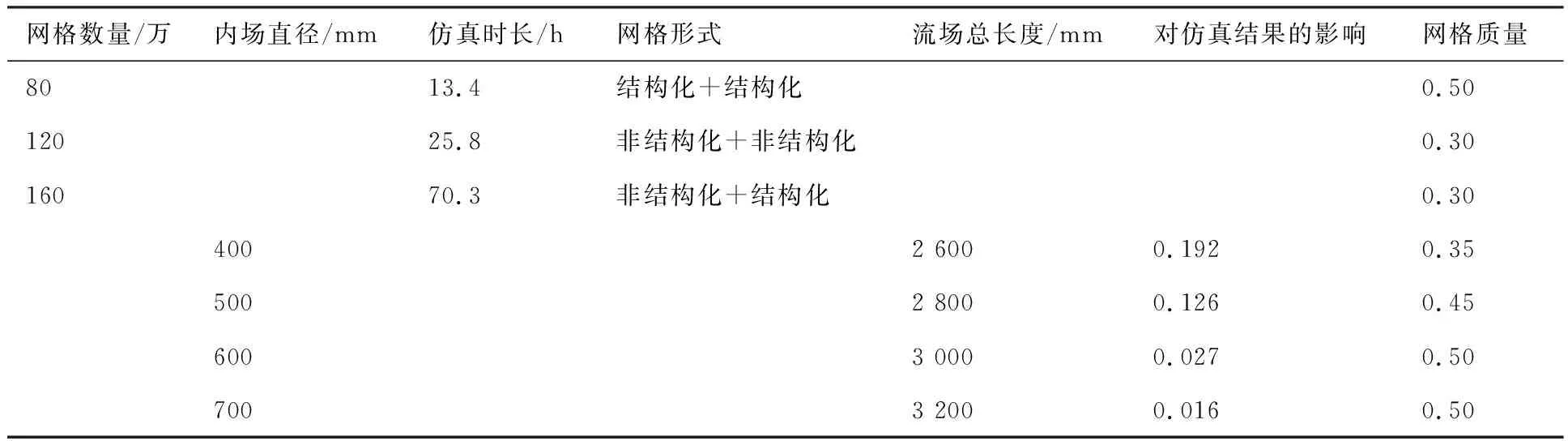
表2 计算网格参数选择对比试验结果Table 2 Test results comparison of parameter selection of computational grid
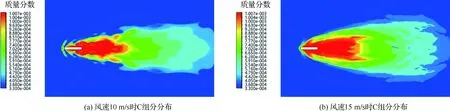
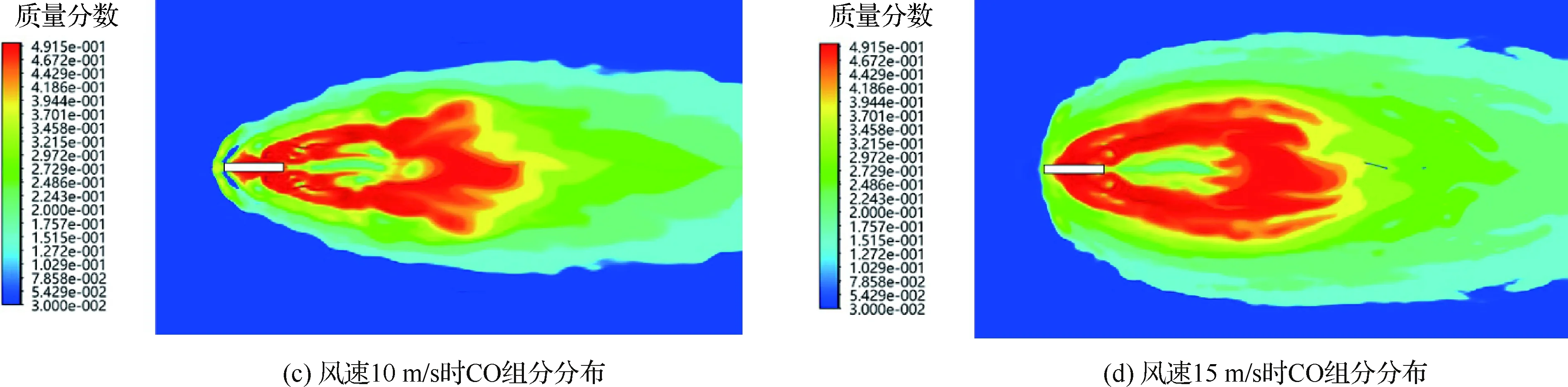
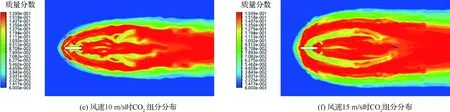



图6 红外诱饵弹尾焰组分分布Fig.6 Component distribution at tail flame of IR decoy
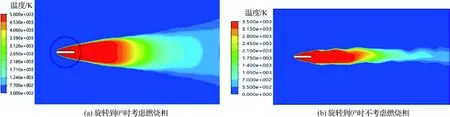
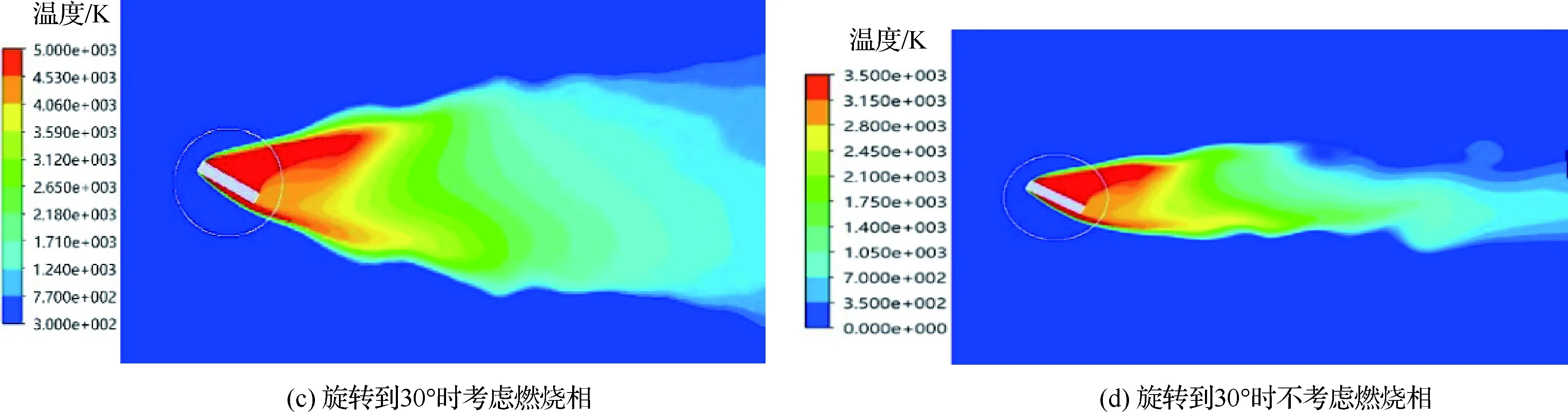
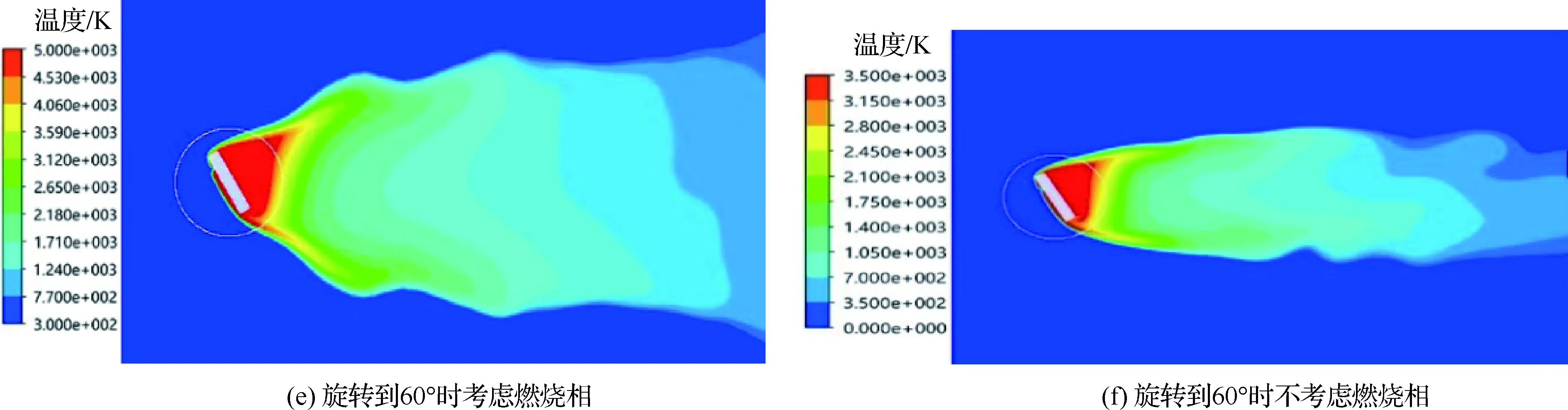
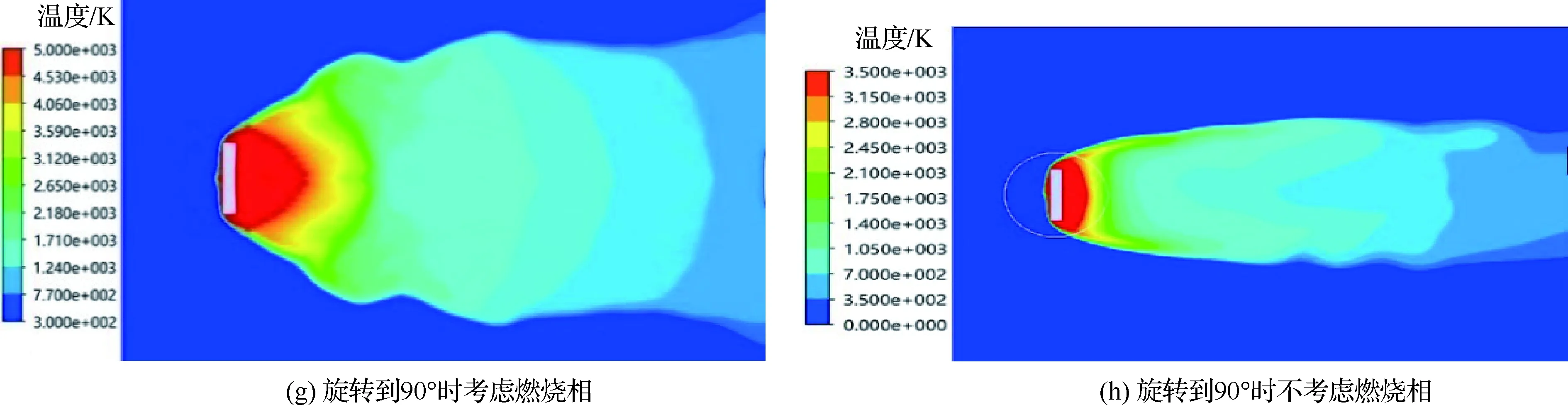
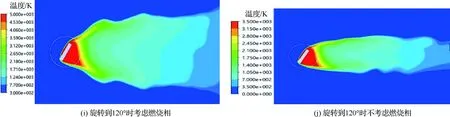
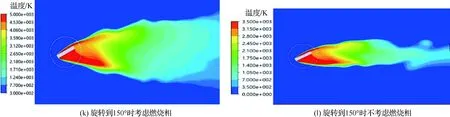
图7 红外诱饵弹温度分布云图的CFD仿真结果Fig.7 CFD simulation results of infrared decoy temperature distribution nephograms
同时,根据图6也可以看出,风速越快,单位时间内燃烧区域会加入越多的氧气,因此弹体周围厌氧区域会缩小,如图6(a)~图6(d)和图6(g)~图6(j)所示;尽管厌氧区域被压缩了,但由于化学反应物总量并没有发生变化,所以在有氧区的化学反应更加剧烈了,因此最终的化学反应产物CO2和MgO生成速度更快,扩散区域更大,如图6(e)、图6(f)、图6(k)和图6(l)所示。
总的来讲,风速越快,组分云图椭度e(即长宽比)越大;反之,图像越趋近于圆形。
随着C颗粒和气态Mg的扩散,它们在经过了“厌氧、有氧交界面”后逐渐进入“有氧区域”。化学过程中的氧化物也逐渐由F变为O。因此在交界面附近,化学反应的中间产物CO和MgF2含量较高,这一特点如图6(c)、图6(d)、图6(i)和图6(j)所示;而在富氧区中,CO进一步与O2反应,全部变成CO2。Mg的所有中间产物与O2反应,最终全变为MgO,这一特点如图6(e)、图6(f)、图6(k)和图6(l)所示。
图7为当诱饵弹的飞行速度为1Ma、弹体旋转速度为1 rad/s时加入燃烧相和未加燃烧相的对比温度云图。从图7可以看出,燃烧相的引入主要导致温度云图出现了一些明显的变化。首先,燃烧相使计算域内高温区域扩大,并且温度的最高值从约3 500 K提高至约5 000 K。这是由于如果不考虑化学燃烧,DPM模型会将喷射颗粒等效为发热颗粒,这时流场的能量来源主要是与颗粒热交换;而燃烧相的加入会使颗粒释放大量的化学能,并使温度进一步上升。因此,温度云图中心温度必然升高,也必将导致作用空域面积增大。
另外,燃烧相的引入使流场中各局部区域因为氧含量不同导致化学反应热略有不同,因此化学反应焓也不同。体现在温度云图上的变化主要就是波动性增强。
3 基于“复合颗粒等效分子黑体模型”的红外辐射特征计算方法
由于建立的仿真模型将用于红外实景仿真系统中,而该系统显示的内容均为红外目标的红外云图。因此,进一步建立非均匀辐射模型计算红外诱饵弹的辐射特征。
红外烟幕内部燃烧颗粒的空间分布具有非均匀性,这将导致烟幕中各处红外光的透射率存在差异。所以空间中的红外烟幕事实上是一种非均匀性半透明红外辐射体。针对这种辐射体,如直接使用Planck定律计算其辐射强度,势必会带来计算上的复杂化,并影响计算精度。
根据上述原因,选用张文华等[26]提出的“等效分子黑体”模型。由于这种模型仅适用于单一直径颗粒的离散相仿真,无法满足复合直径颗粒的计算场景,本文在原有模型的基础上进行了复合颗粒喷口型扩展,从红外烟幕计算红外烟幕的辐射特征,并成功获得红外烟幕的红外分布云图。然而,张文华等[26]规定了所有颗粒的物理特性均相同,因此为了满足计算需求,扩展并建立了“复合颗粒等效分子黑体”算法。
将流场在空间上被划分为大量边长为D的“微元”,如图8所示,每个微元中都包含不确定数量的辐射颗粒。流场中每一个辐射体都存在它对应的“等效辐射面积”,例如可以假设某一个颗粒的辐射面积为A,某一个“微元”的辐射面积为S。
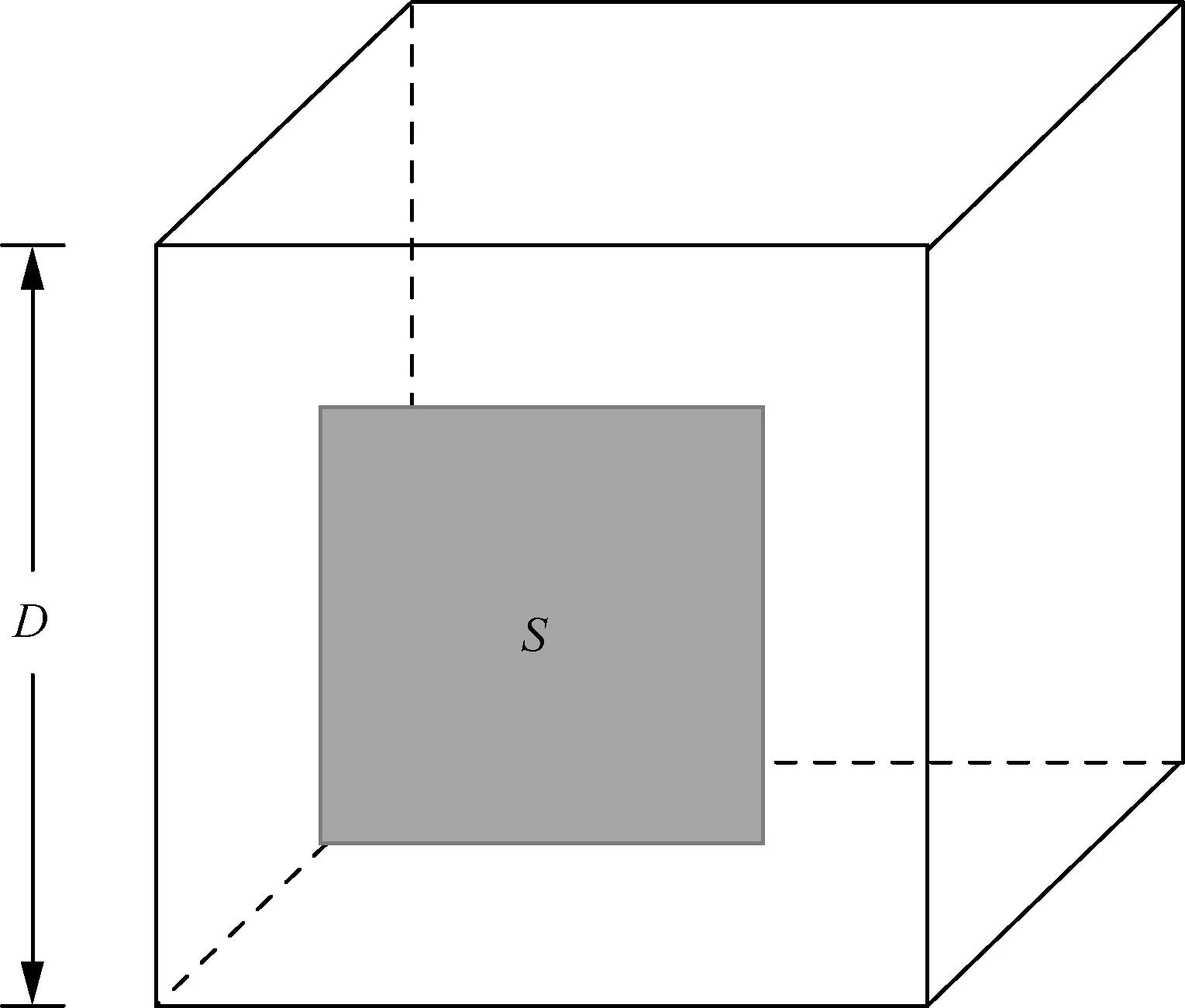
图8 微元结构Fig.8 Structure of micro unit
基于这种方法的“遮挡原理”,每个颗粒对应的辐射面积均被假设为非透明体。因此,当空间中的多个颗粒互相发生遮挡(如图9所示的3个颗粒发生遮挡)时,它们对应的“等效辐射面积”总和Athree=A1+A2+A3。
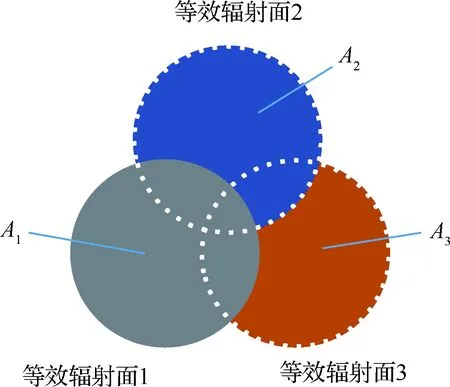
图9 发生遮挡时的等效辐射面图Fig.9 Equivalent radiation surface map in occlusion
由于增强型DPM将颗粒分为了多组,每一组中的所有颗粒均具有完全相同的物理特征(ρn,Tn,pn),因此第n组颗粒对应的微元的密度就可以被表示为
(24)
式中:Mn为该微元中第n组颗粒的数量。
根据“复合颗粒等效分子黑体”法的“遮挡原理”,由第n组颗粒产生的等效黑体辐射面积总和可以被表示为
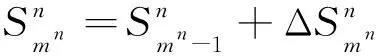
(25)
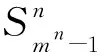

(26)
在计算了一个“微元”中第n组颗粒产生的等效辐射面积后,进一步计算红外烟幕的整体辐射特征。首先,整个计算域被划分成I×J×K个微元,如图10(a)所示,其中每一个微元的边长仍为D;然后,取其中一列作为研究对象,如图10(b)所示,此列中第k个微元的等效辐射面积可以根据式(27)计算求得:
(27)
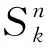
根据式(27),第k个微元的辐射面积通量可以表示为
(28)
式中:lk为第k个微元的辐射平面边长;d为等效辐射体边长。
根据式(28),一列微元辐射量可以通过式(29)计算求得:
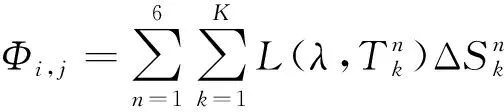
(29)
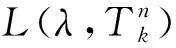
(30)
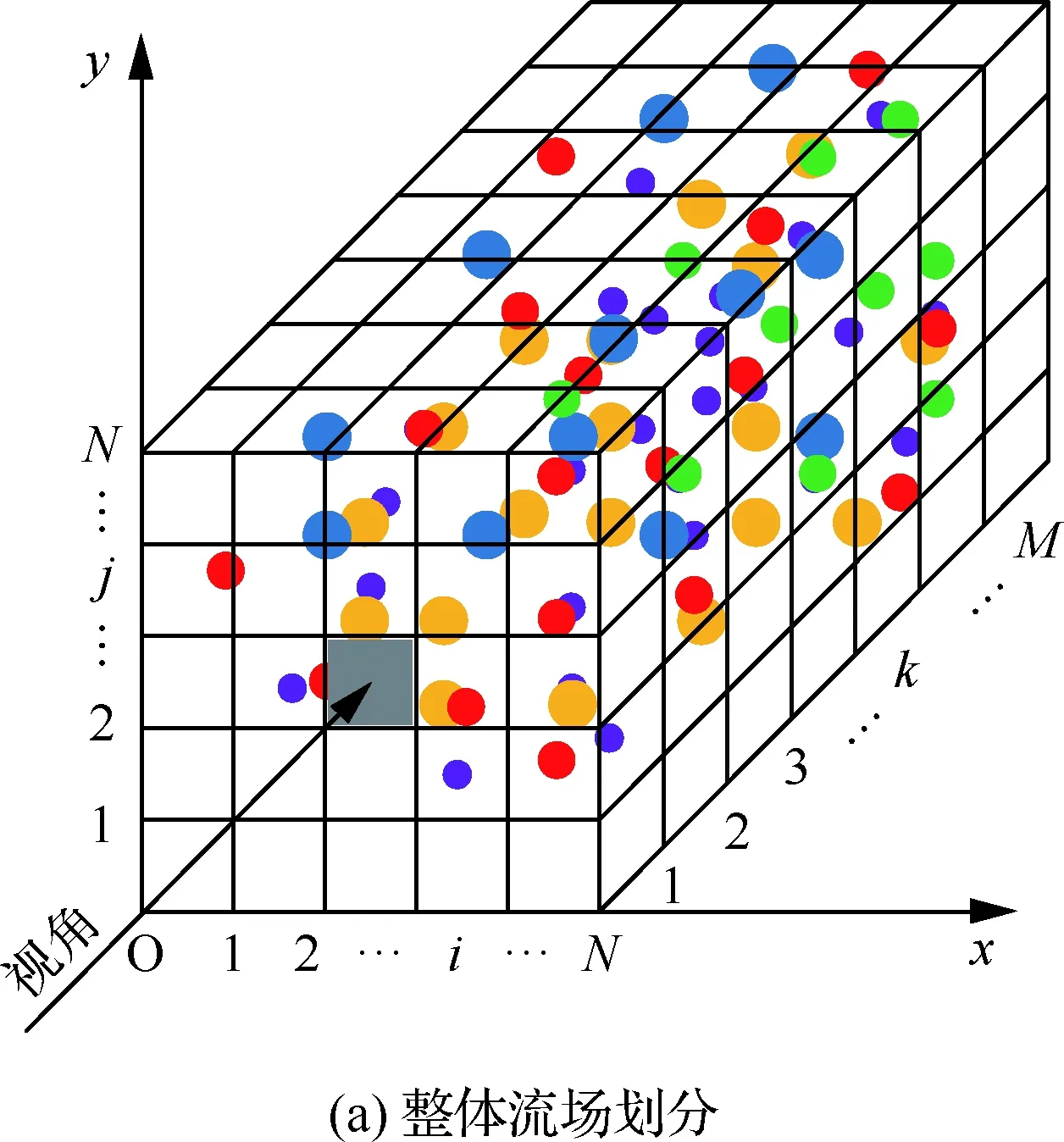
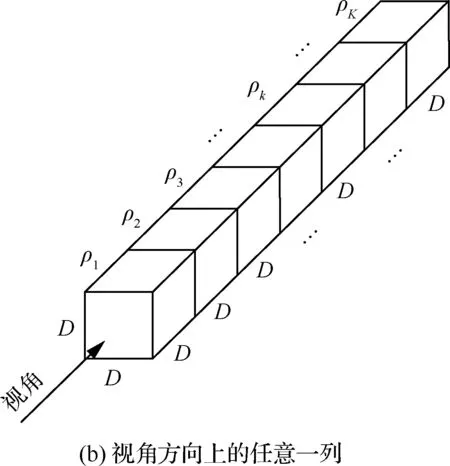
图10 扩展型“等效分子黑体”模型结构示意图Fig.10 Structural schematic diagram of extended “equivalent molecular blackbody” model
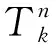
因此,红外烟幕的红外特征就可以通过式(31)计算求得:
(31)
弹体参数、计算域条件和初始化条件如下:弹体尺寸为∅50 mm×300 mm,弹体飞行速度为1.2Ma, 海拔高度为5 000 m,组分为Mg和Al。在建立了扩展性“等效分子黑体”模型后,根据弹体参数仿真得到了4种不同弹体旋转速度对应的红外诱饵弹的红外云图,如图11所示。
图12所示为转速为0时不同时刻诱饵弹辐射特征光谱图。可知,4 s时诱饵弹已经处于稳定燃烧状态,燃烧可以一直持续至14 s。
另外,诱饵弹分别在波数约为1 000 cm-1和2 300 cm-1处辐射特征较为明显,这与林长津[27]的实验结果变化趋势相符。
4 实验验证
为验证所提模型的仿真精度,设计了两组实验,从图形特征角度验证红外诱饵弹的仿真精度。
Labonté和Deck[28]提出了一种径向基(RBF)神经网络结构以及12种图形特征用于辨识同一幅图像中的红外目标与红外诱饵弹。仿真结果表明其中6种图形特性的辨识率达到94%。因此,分别使用这6种图形特征对比实验图像与仿真图像的相似度。这些参数的定义详见表3。
设计两组对比实验:实验1的实验环境为多云,高空风速36 m/s,诱饵弹飞行速度0.97Ma;实验2的实验环境为晴天,高空风速19 m/s,诱饵弹飞行速度0.87Ma。
为验证燃烧对红外图形特征的影响,分别针对实验1和实验2设计了两组对比实验。实验结果如表4所示。可以发现由于红外药剂的燃烧产生大量高温燃气,这些高温燃气将直接增大红外目标在整体图像中的面积,这直接影响了离心率e和半径R两个特征,从而明显提高了红外模型的仿真精度。
针对这种两组实验条件的仿真结果如图13所示。可以看出,风速对于诱饵弹成像是有影响的。风速越快时,弹体尾焰拖尾越长,这是由于更快的风速在单位时间内引入了更多的氧气,导致化学反应的厌氧区被压缩;同时更快的风速也会促使有氧区与周边热交换速度更快。

图11 不同初始条件下的红外诱饵弹仿真结果Fig.11 Infrared decoy simulation results under different initial conditions
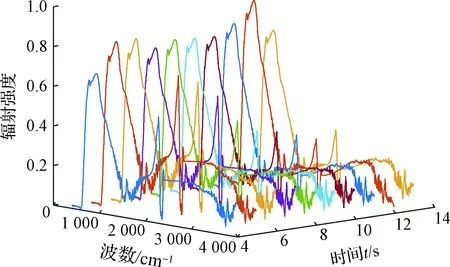
图12 MTV烟火剂颗粒在不同时刻燃烧的光谱变化情况Fig.12 Spectral changes of MTV pyrotechnic particles during combustion at different times
在对比风速对仿真结果的影响后,继续跟进实验1和实验2的工况,对比研究了化学燃烧相加入前后对仿真结果的影响。对比实验分别选取起燃时刻和稳定燃烧时刻作为研究对象,结果如图14所示。
通过观察对比实验结果,可以发现如下3个特点:
1) 在起燃时刻,未加入燃烧相的诱饵弹图像特征更为明显。这是由于未加入燃烧相时,DPM模型将颗粒初始状态假设为高温颗粒。这些高温颗粒在与周围流场换热后逐渐冷却,最终失去红外特征;而考虑燃烧相的DPM模型将颗粒的初始状态假设为常温状态,通过剧烈的化学反应释放化学能,从而产生红外特征。这就导致起燃时刻未加入燃烧相的仿真结果更为明显,这也更符合真实物理过程。
2) 稳定时,加入燃烧相的仿真结果红外特征更为明显。这时由于燃烧相对附加化学能,导致反应焓释放更多热量。因此其仿真结果中,反应持续时间更长,能量更高。
3) 整个仿真过程中,加入燃烧相后,红外目标边缘更加不规则。这是因为仿真流场中出现了大量未完全反应的中间产物,这些中间产物对氧

表3 评价红外图形特征时所用的参数定义
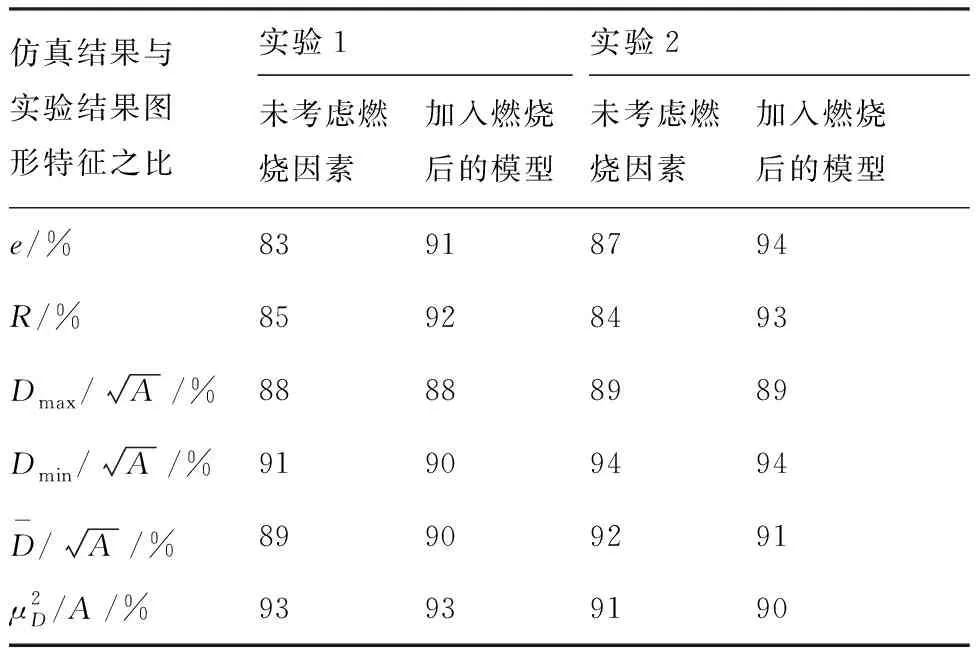
表4 燃烧因素对实验结果的影响
气的需求和消耗能力均不相同,因此常常会导致流场中各点反应强度不同,最终导致红外图像的边缘不规则。而对于未加入燃烧相的DPM模型,其辐射机理是热传递,因此产生辐射的过程较为平缓。所以边缘相对规则。
再根据图13和图14所示结果进行分析后,结合表4的结果可以发现,由于引入了化学燃烧因素,红外诱饵弹的图形特征相似度有明显提升,部分参数的相似度可以达到8%。

图13 考虑了燃烧相的仿真结果Fig.13 Simulation results with combustion phase


图14 燃烧相加入前后DPM模型仿真结果对比Fig.14 Comparison of DPM model simulation results before and after addition of combustion phase
5 结 论
红外诱饵弹建模对红外制导算法研究和红外诱饵弹优化研究具有重要意义。在增强型DPM红外诱饵弹动态建模方法的基础上,进一步研究了红外烟火剂的化学燃烧对诱饵弹的红外特征产生的影响。
1) 在原有模型的基础上,通过研究化学反应机理建立了MTV颗粒在“气”与“固”相交界面处的化学反应方程式,并加入了化学组分守恒定律和能量守恒定律,计算得到了化学反应的焓变,进而建立了基于化学燃烧和增强型DPM模型的红外诱饵弹模型。
2) 通过数值仿真的方式计算得到了诱饵弹尾焰中各化学组分分布情况,验证了模型中燃烧相相关研究的准确性。
3) 建立了“复合颗粒等效分子黑体辐射”模型,并计算得到了不同时刻诱饵弹的光谱分布特征。经过与文献中的实验结果进行对比验证了辐射特征的准确性。
4) 设计对比实验验证了风速对红外模型的影响和加入化学燃烧相后模型仿真结果的变化,结果显示燃烧相的加入使模型精度得到了进一步的提高。
