展向振荡对激波/湍流边界层干扰的影响
2020-12-29孙东刘朋欣童福林
孙东,刘朋欣,童福林
中国空气动力研究与发展中心 空气动力学国家重点实验室,绵阳 621000
激波/边界层干扰是一类广泛存在于超/高超声速流动的复杂流动现象。由于它可能会带来总压降低、流动非定常振荡、局部高热流等负面效应,因此对飞行器的气动特性和飞行安全有重要的影响,是高速飞行器设计中必须考虑的关键问题。激波/边界层干扰非定常特性问题自发现以来就受到了广泛的关注。
对于激波/边界层干扰的非定常特性,早期的实验认为激波的低频特性主要来自于来流湍流边界层中的脉动。Erengil和Dolling[1]通过测量间歇区域内压力变化得到激波足的位置和速度,观察到激波足的速度与来流压力脉动具有清晰的相关性。Brusniak和Dolling[2]应用互相关方法将不同壁面位置的压力信号做相关性分析,认为自由来流边界层内的压力信号与间歇区、分离区内的压力信号之间是存在关联的。Hou等[3]通过测量间歇区压力来确定激波足的瞬时位置,结果表明激波运动与来流边界层的厚度具有一定的关联。Ganapathisubramani等[4]在实验中观察到在边界层对数区内存在较长拟序结构,并认为自由来流湍流边界层中的拟序结构是诱导激波低频振荡的主要原因。Humble等[5-7]指出分离流动与湍流边界层中的低速结构密切相关。他们的实验结果还显示上游的速度脉动与分离位置存在明显的相关性,这也与Ganapathisubramani等[4]的研究结果较为一致。但在最近的直接数值模拟和大涡模拟发现,下游分离泡与激波的低频运动存在着密切的联系。Pirozzoli和Grasso[8]对马赫数Ma=2.25的斜激波入射激波/边界层干扰开展了直接数值模拟研究,认为分离泡的振荡与方腔流动中的Rossiter模态类似,并提出“声反馈机制”。Touber和Sandham[9]对斜激波入射激波/边界层干扰开展了大涡模拟研究。他们并没有发现Ganapathisubramani等[4]在实验中观察到的拟序结构,并且他们认为分离泡内的全局不稳定性可能是激波/边界层干扰非定常运动的驱动机制。此外,童福林等[10-13]开展了大量的激波/湍流边界层干扰直接数值模拟研究,探讨了干扰过程中激波强度、壁面温度、马赫数等因素对干扰区内复杂流动现象的影响规律。
随着对激波/边界层干扰机理研究的深入,为了降低激波/边界层干扰非定常运动对飞行器性能的不利作用,研究人员开展了流动控制研究并取得了较大进步。早期控制手段主要以吹吸气为主[14],这种方式确实能够实现对分离泡的有效控制,但需要耗费大量的能量,影响飞行器飞行效率。近年来,微型涡流发生器作为一种被动控制手段受到广泛重视,人们对其外形高度[15-16]、安装位置[15]和控制机理[15-17]都进行研究,但Babinsky[15]和Giepman[16]等发现它并不能完全消除分离,只能够调节分离区沿展向的分布。周期振荡平板作为一种广泛研究的减阻手段是Junge等[18]通过直接数值模拟的方式发现的。Junge等[18]发现当槽道下平板以一定频率和幅值发生周期振荡时,壁面上的摩阻会显著降低。Laadhari等[19]对更大雷诺数的槽道开展了相关实验,发现速度梯度在振荡壁面附近降低并且湍流强度也会降低。Choi[20]对展向振荡的平板开展了相关实验,实验发现展向振荡壁面能够降低湍流强度。Choi推测是由于展向涡量减小了黏性底层内的平均速度梯度造成了阻力的减小。Choi等[21]进一步给出了展向振荡引起阻力减小的关系式。Dhanak和Si[22]则认为阻力的减小是拉伸的流向涡与底层Stokes层相互作用的结果。Fang等[23]采用展向振荡壁面控制超声速边界层壁面热流,并通过数值模拟显示了明显的控制效果。Yao和Hussain[24]对马赫数0.3、0.8和1.5的可压缩槽道进行了直接数值模拟,结果显示当马赫数为0.3和0.8时,摩阻减小量随着振荡周期的增加而增加;当达到极大值后,开始减小。而马赫数1.5情况下,摩阻减小量没有出现上述现象,而是一直随着振荡周期的增加而增加。
由于激波/边界层干扰的流动分离和激波非定常运动都与壁面特性密切相关,而振荡平板正是影响着壁面附近的流动特征,因此开展两者之间的相互影响的研究有着十分重要的意义。本文采用高精度直接数值模拟的方式对发生在振荡平板上的入射斜激波/边界层干扰现象进行了研究。本文内容安排如下:第1节介绍计算采用的数值方法和计算设置;第2节研究了展向振荡对流场结构的影响,并解释了其中的影响机制;第3节从物面压力和物面剪切的非定常特性和统计特性方面给出了展向振荡的影响;第4节对物面压力和剪切的脉动量进行了本征正交分解,得到了在展向振荡情况下的本征正交分解主模态变化特性。最后,第5节给出结论。
1 计算参数
本文计算采用的控制方程为曲线坐标系下的无量纲三维可压缩Navier-Stokes方程,其具体形式为
(1)
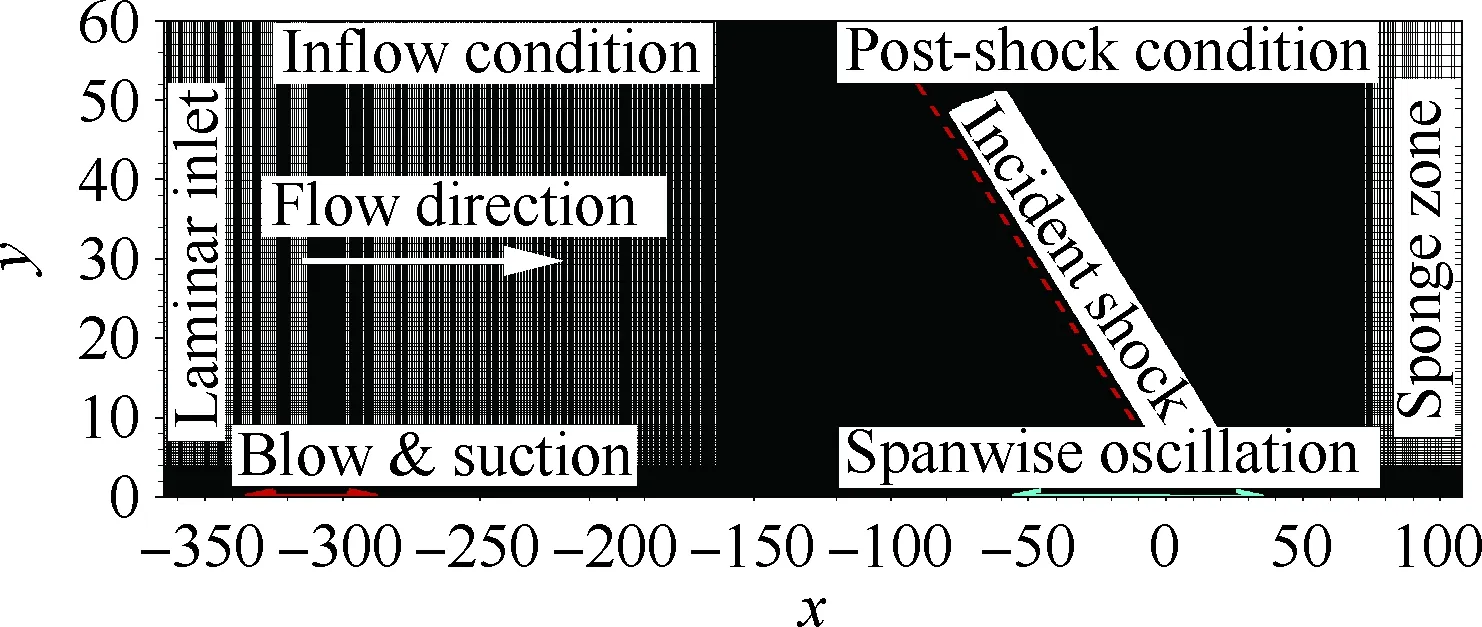
图1 计算设置示意图Fig.1 Sketch of computation setup
(2)
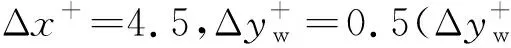
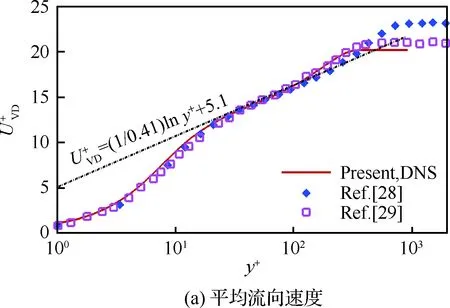
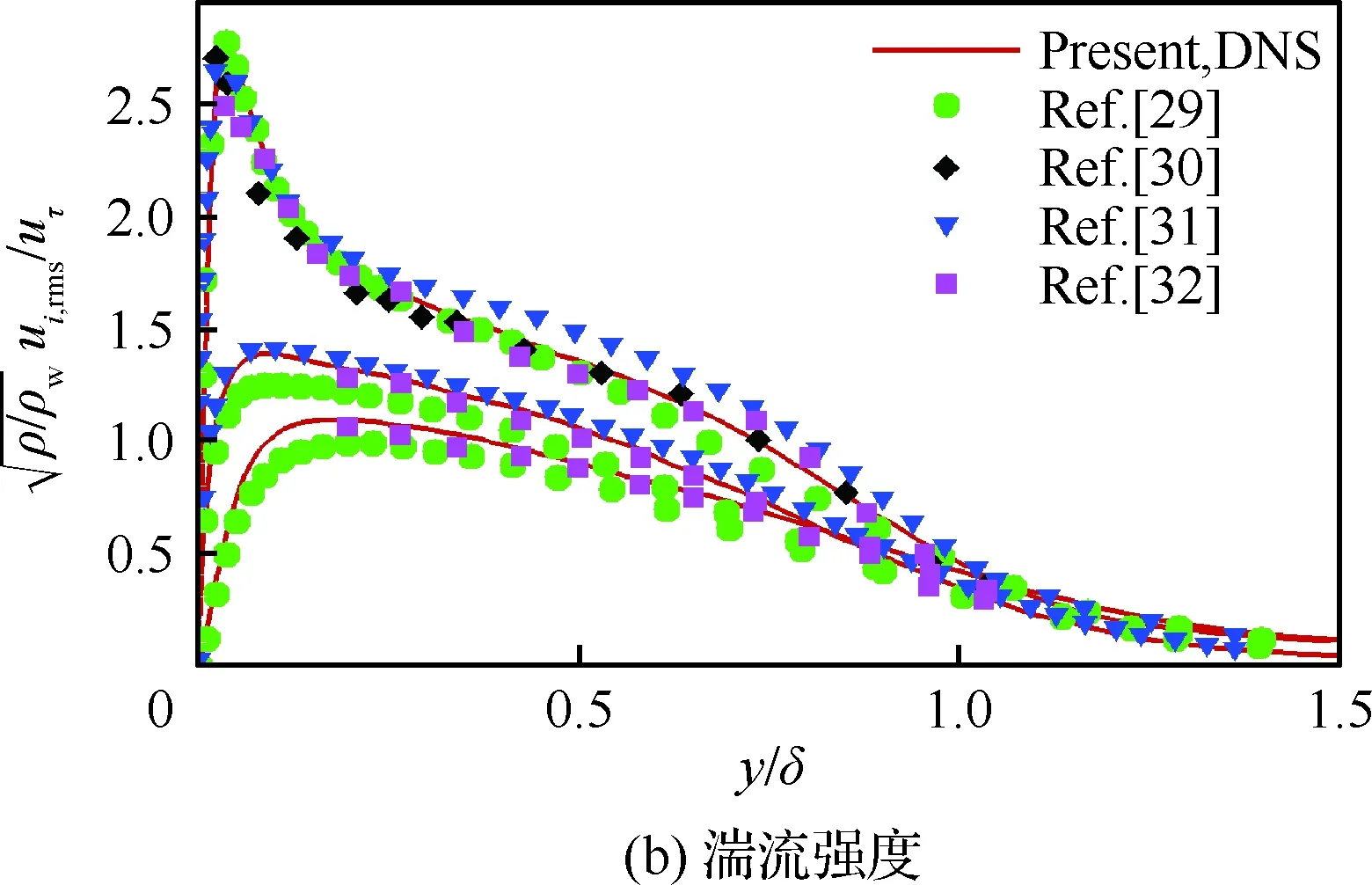
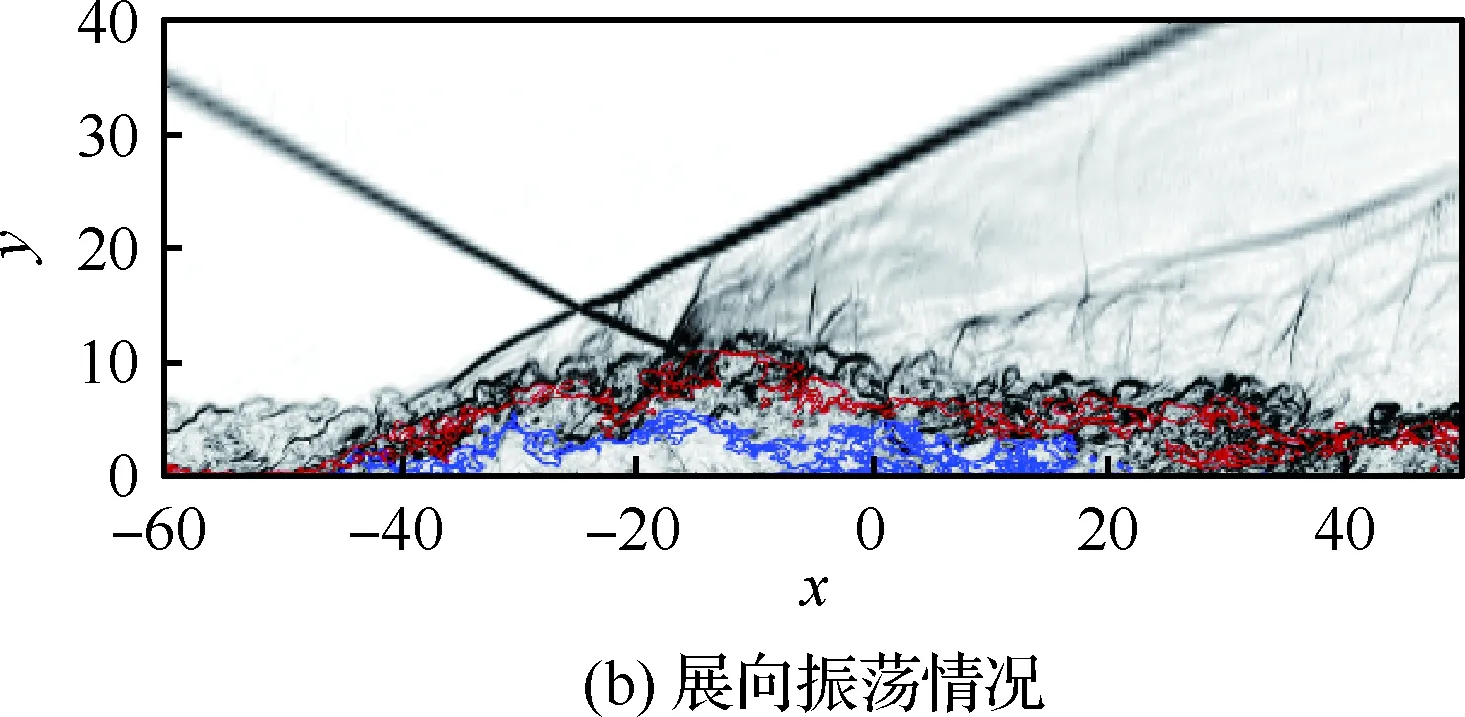
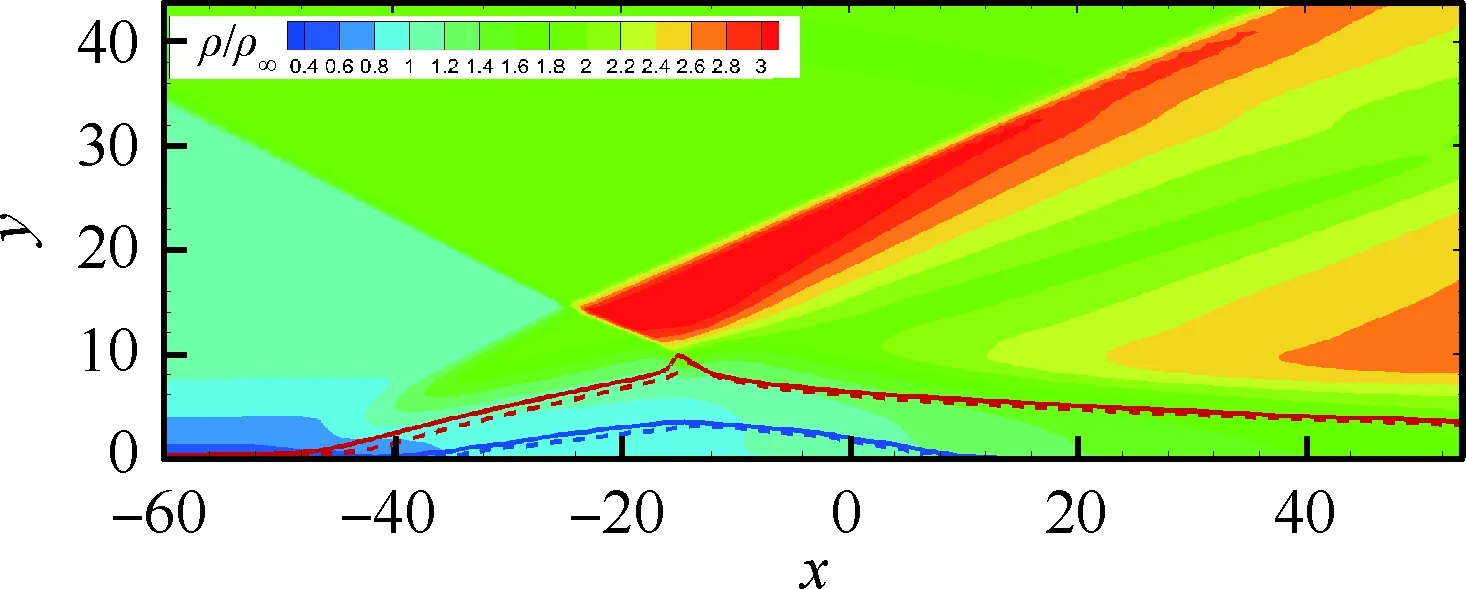
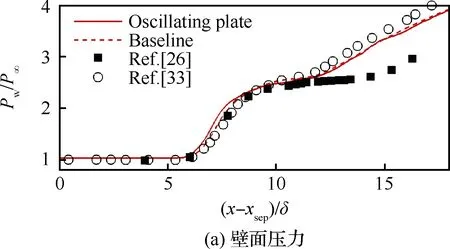
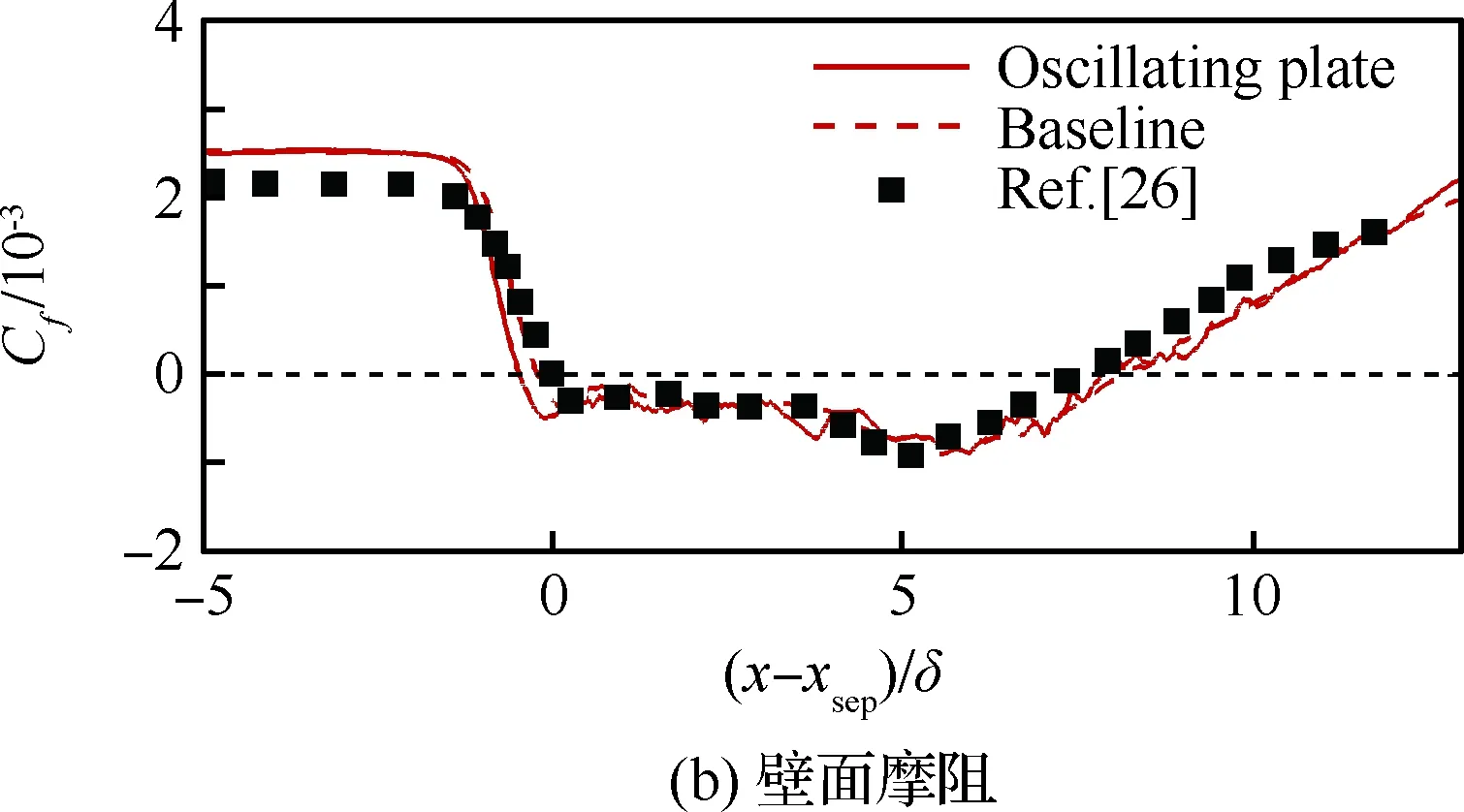
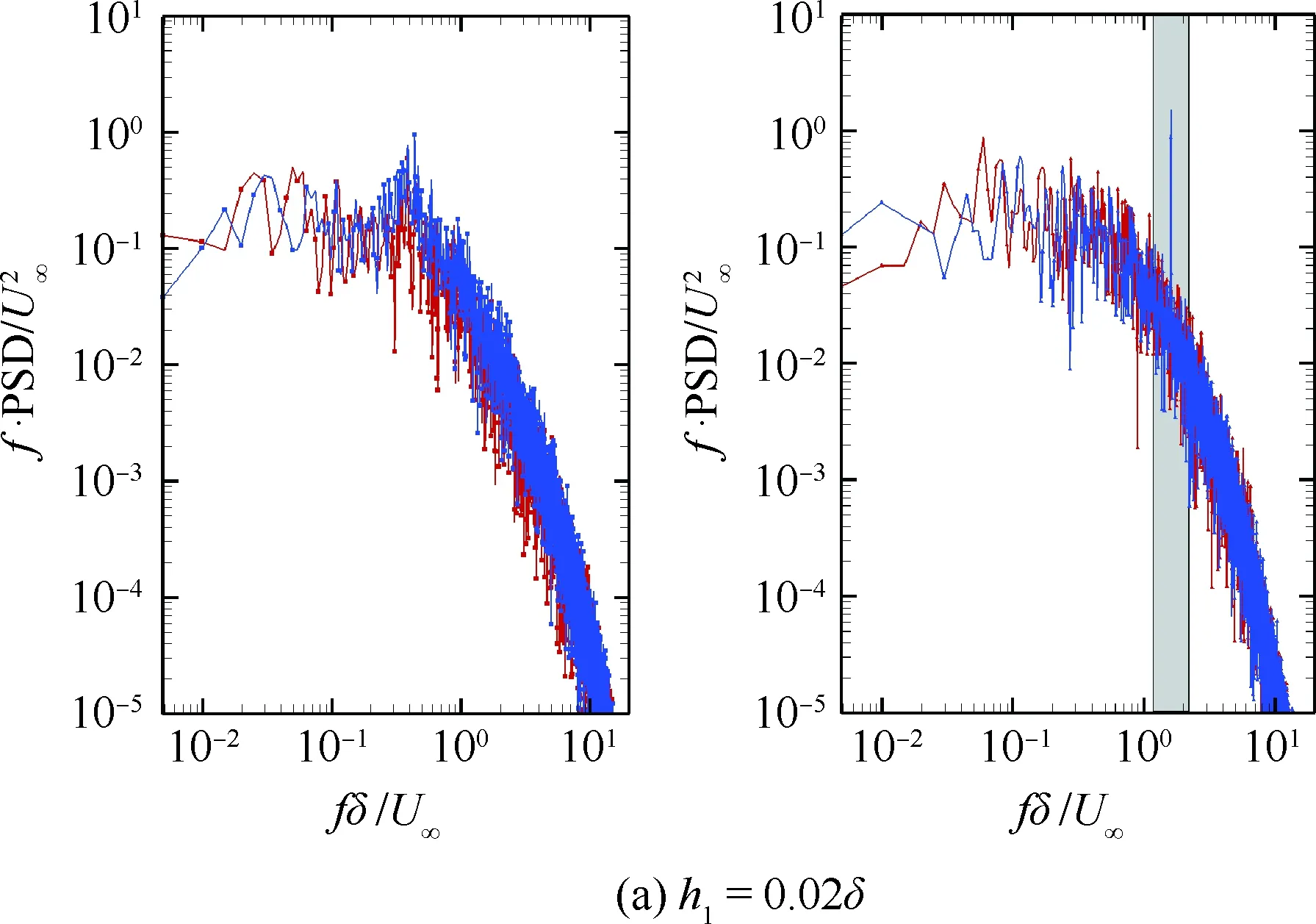
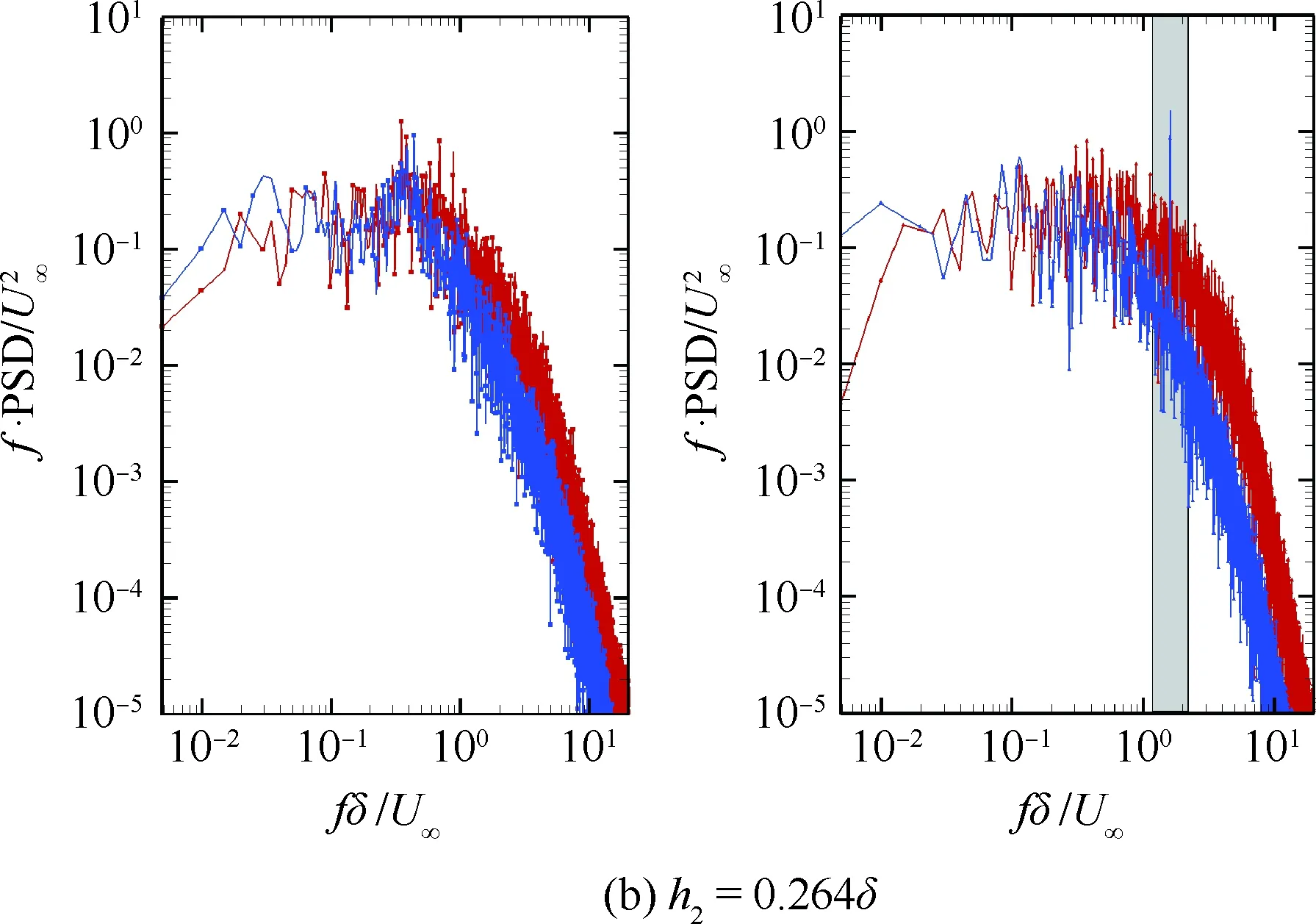
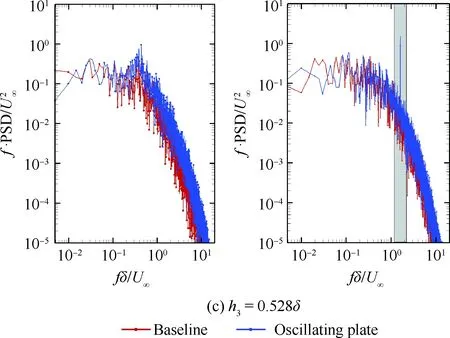
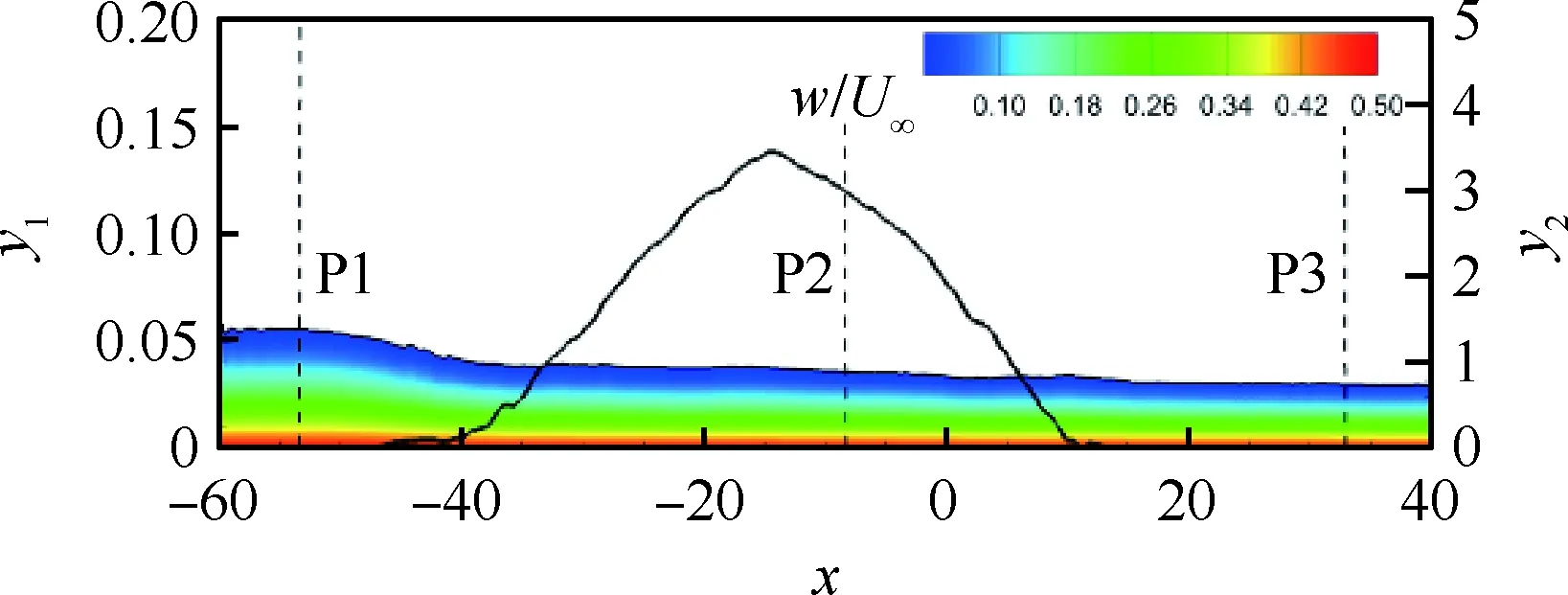
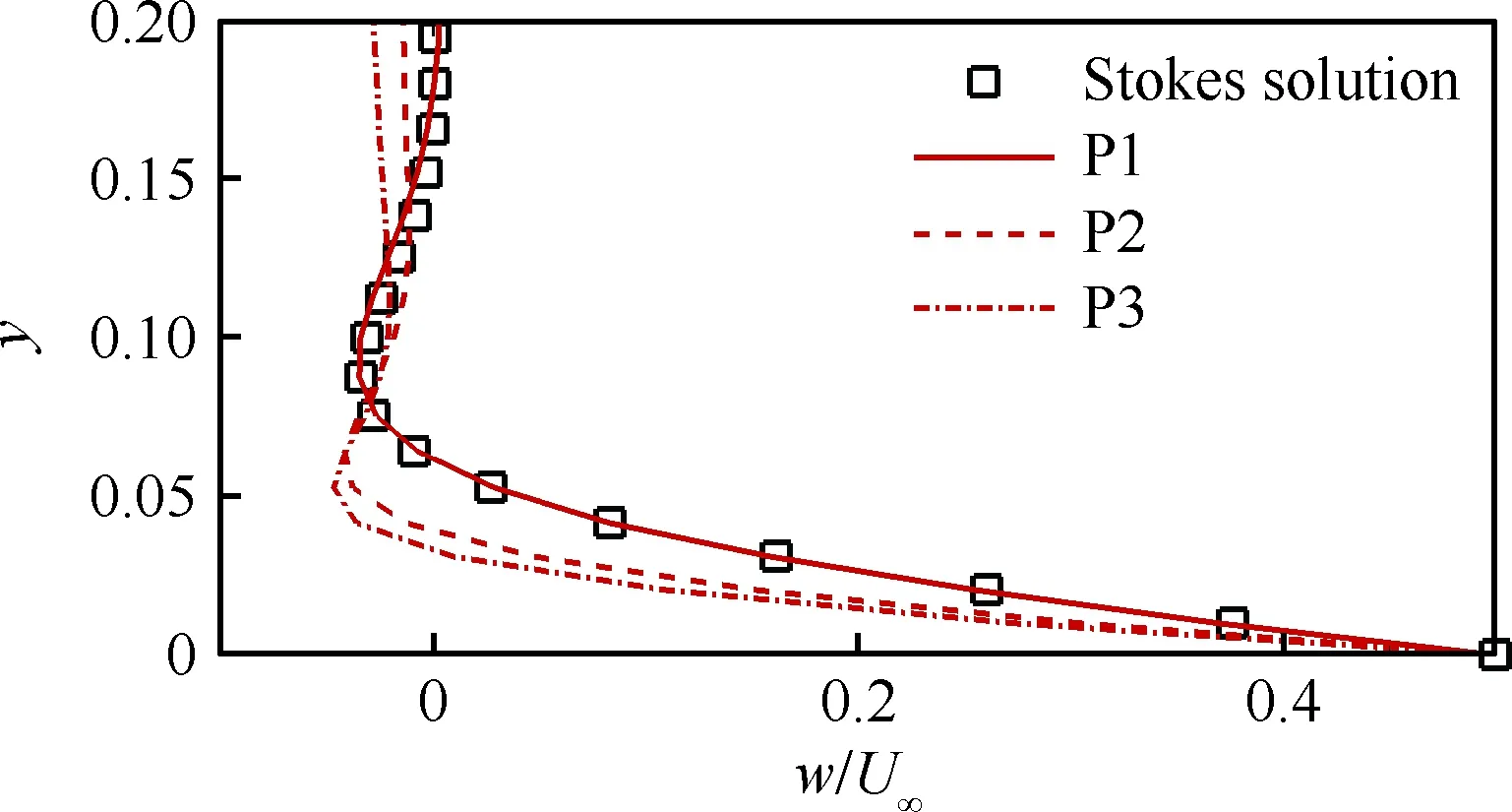
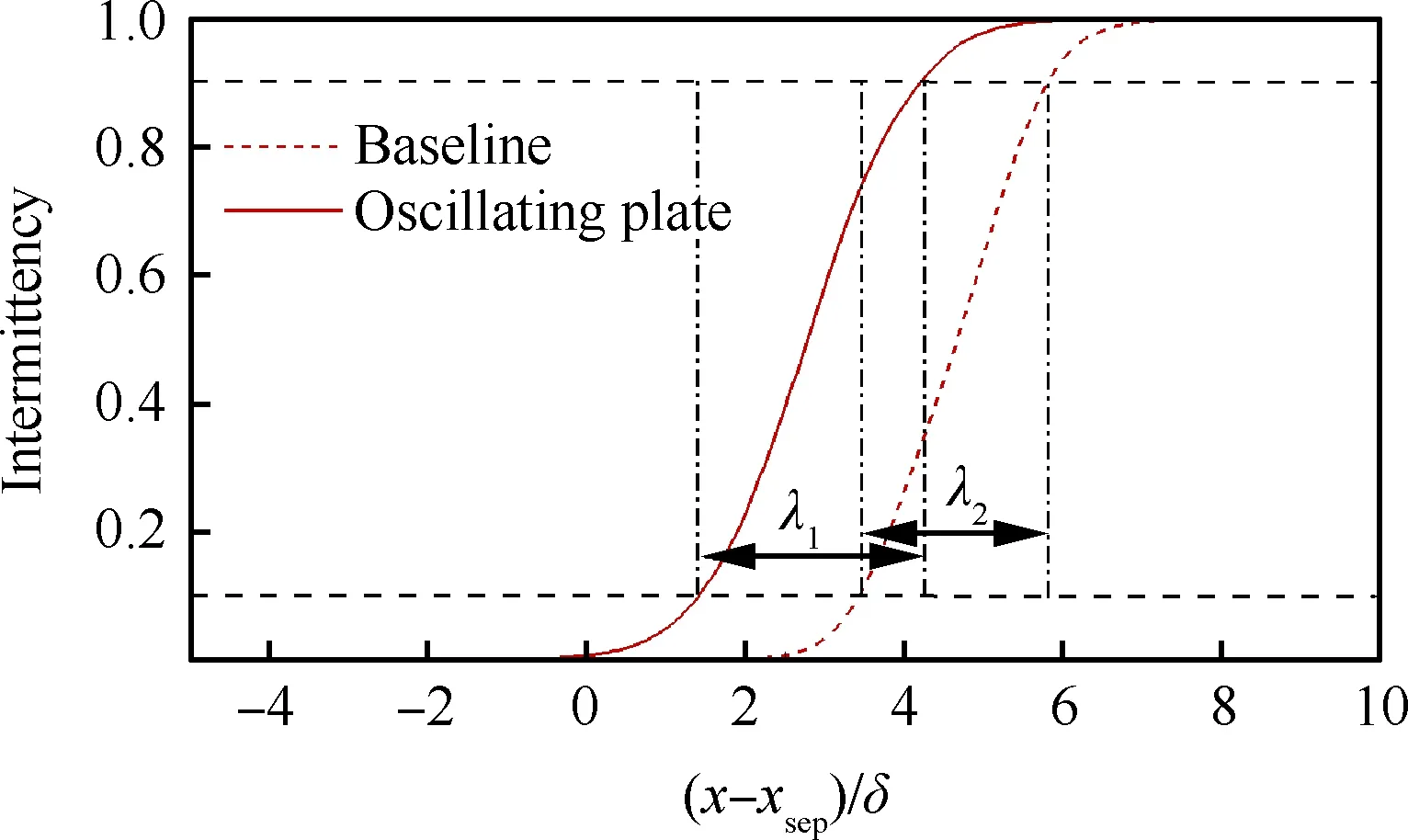
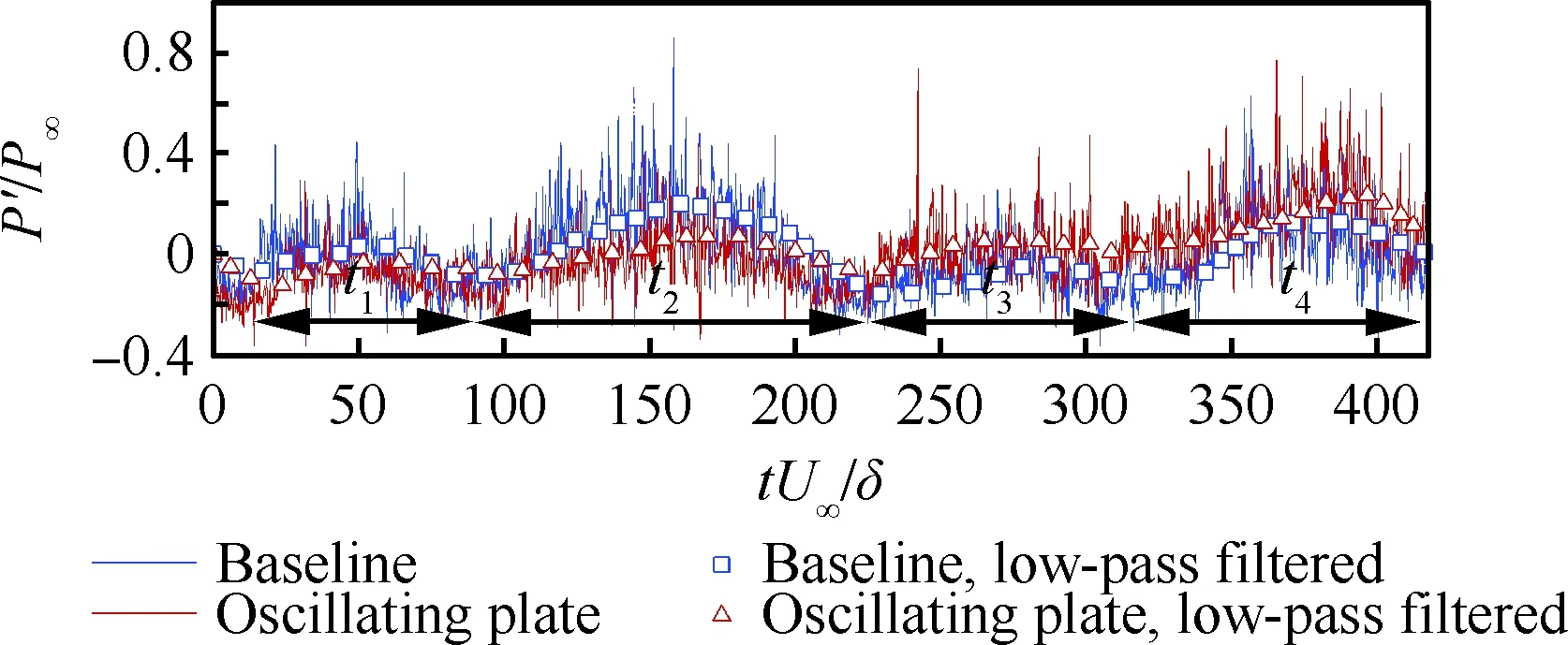
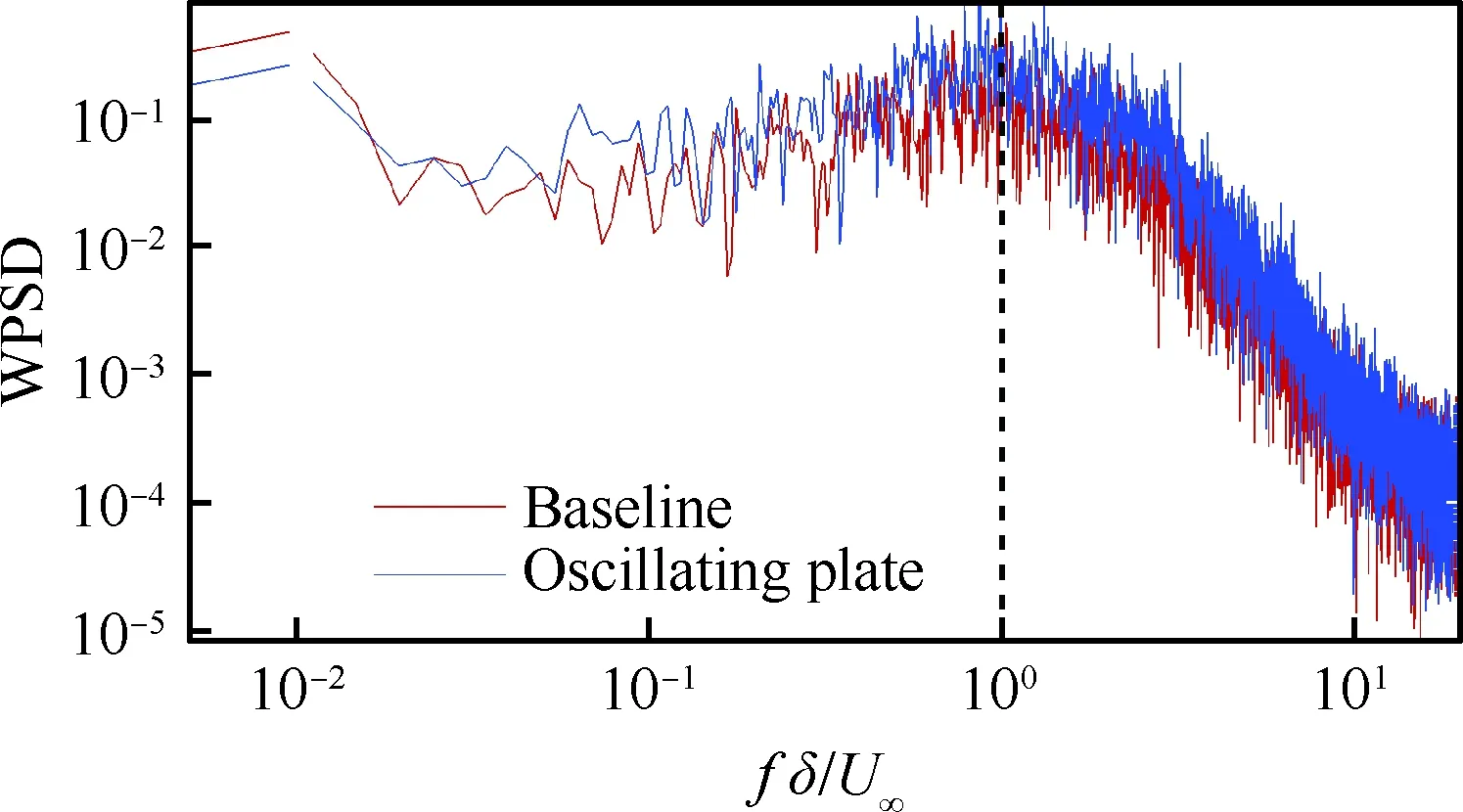
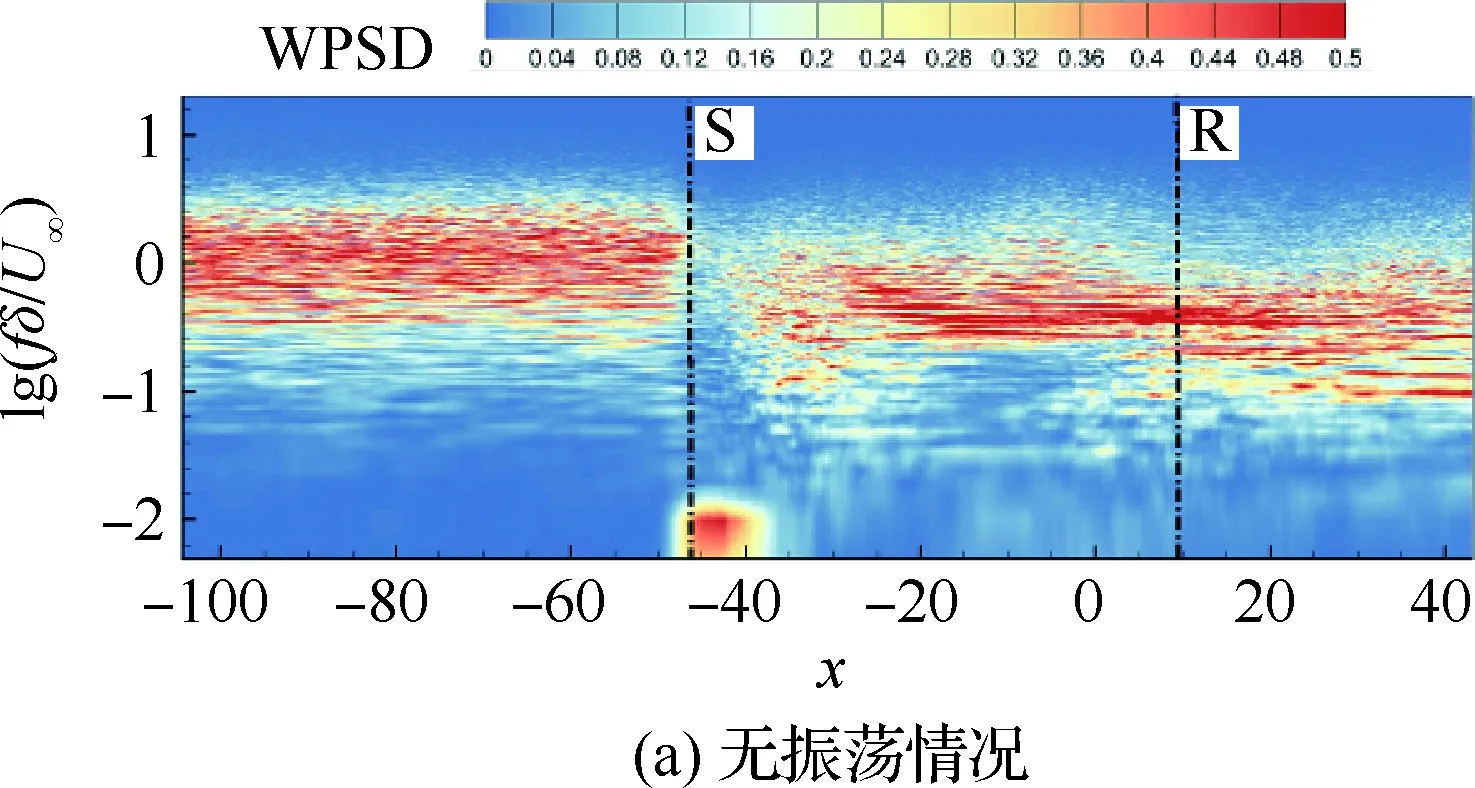
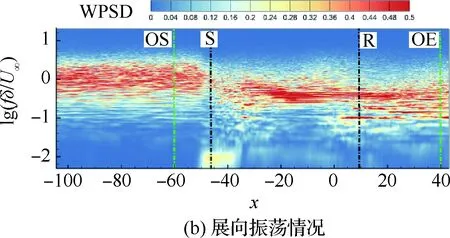
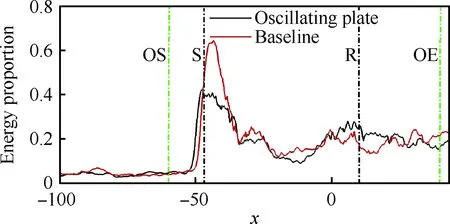
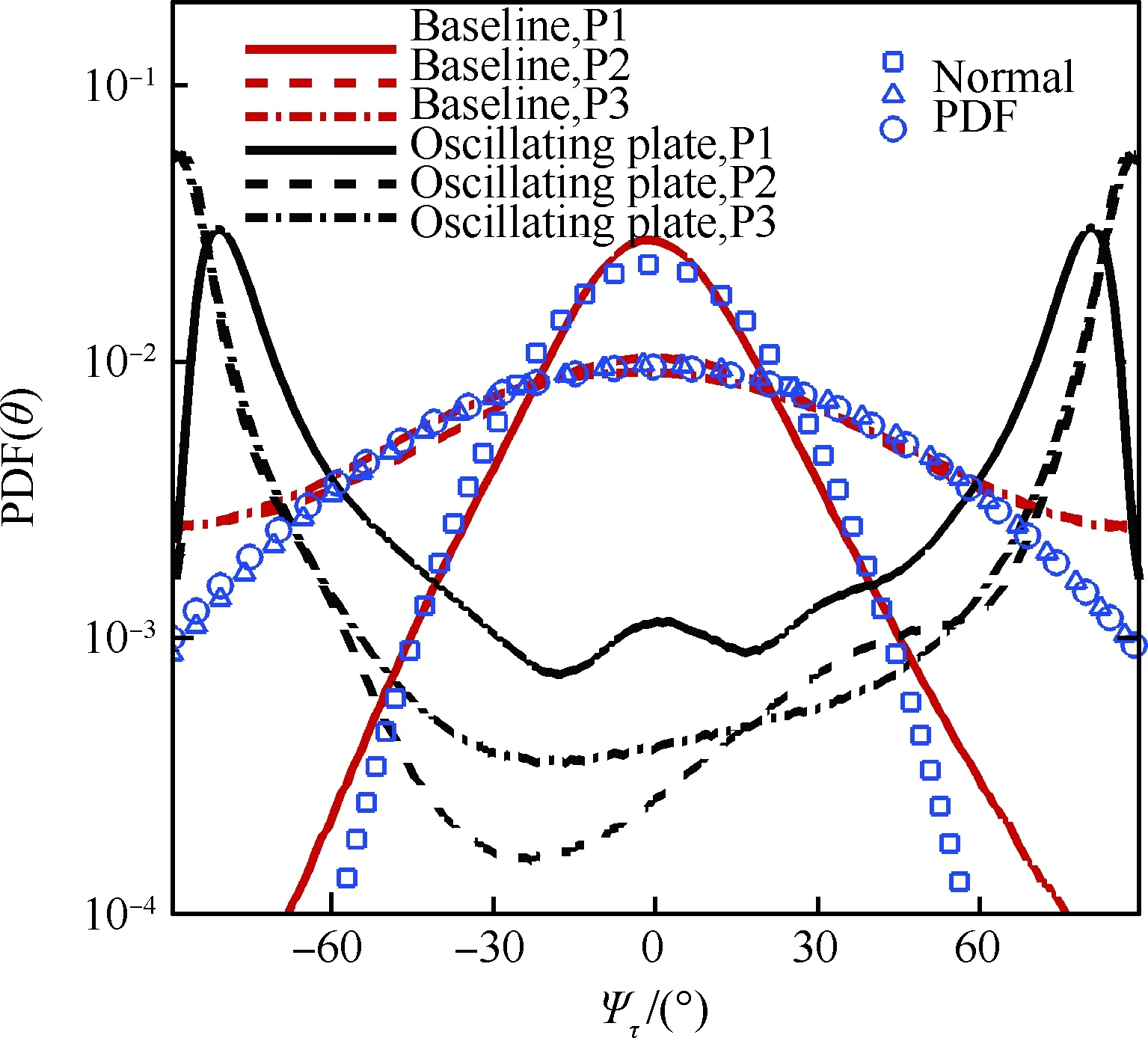
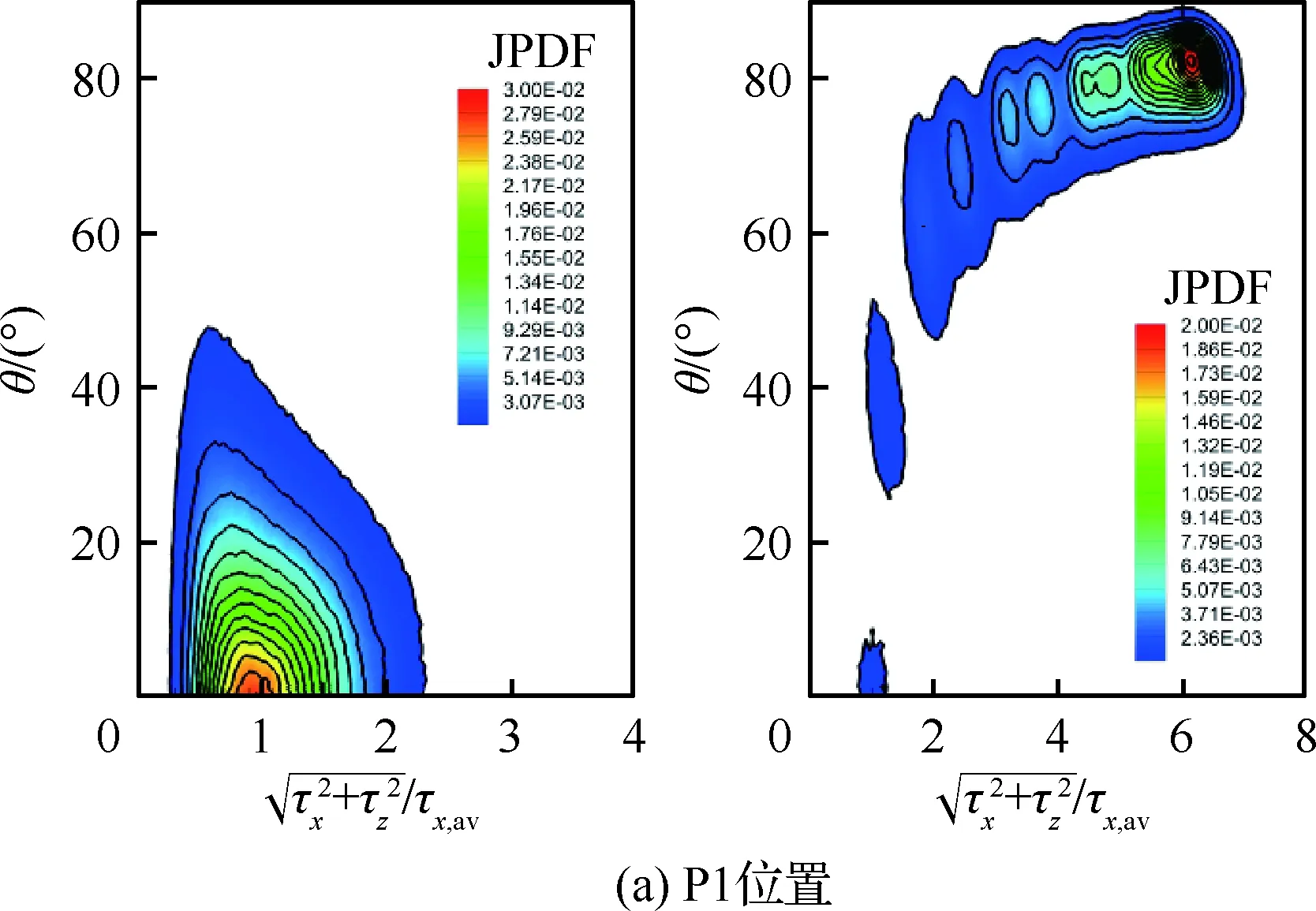
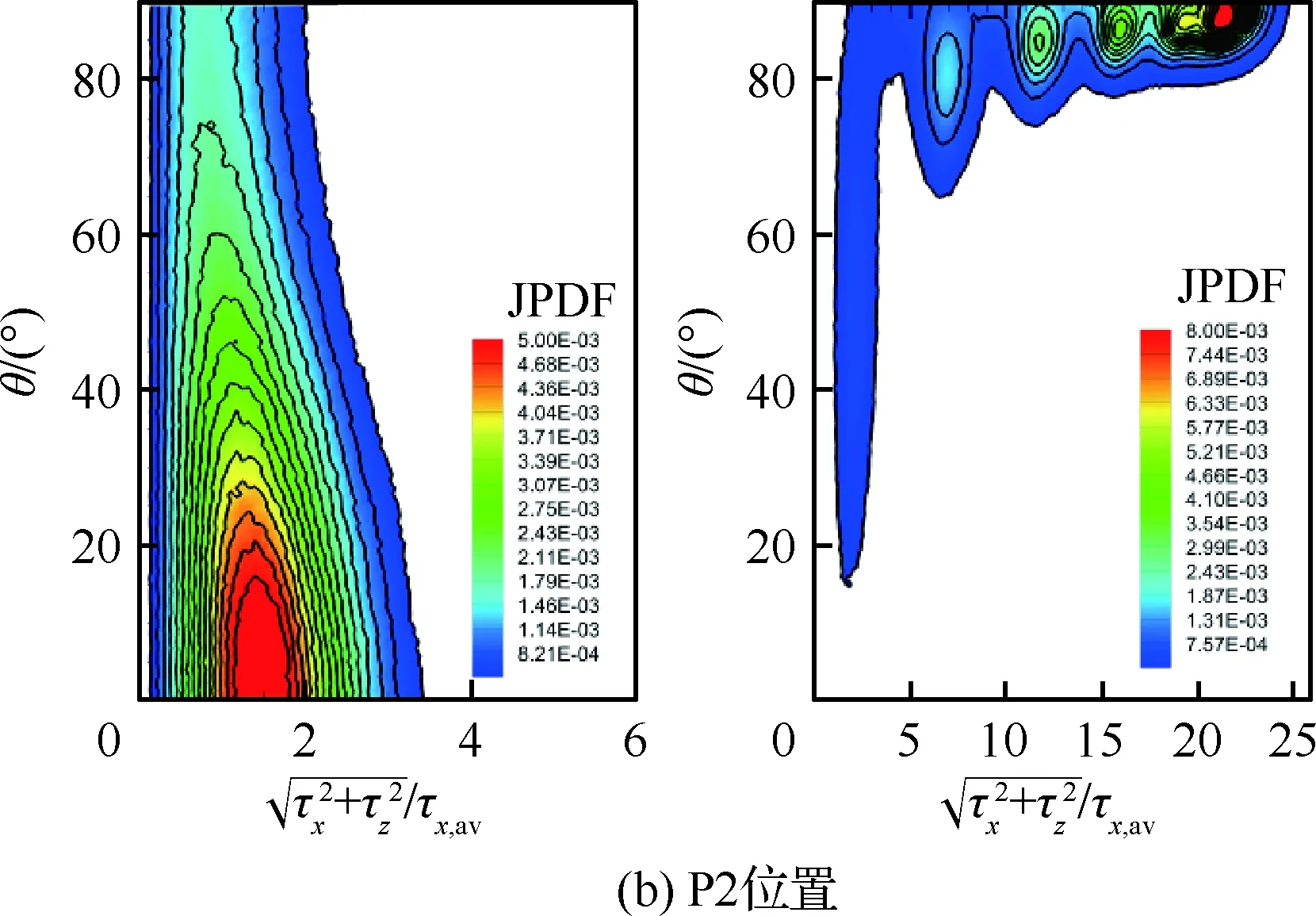
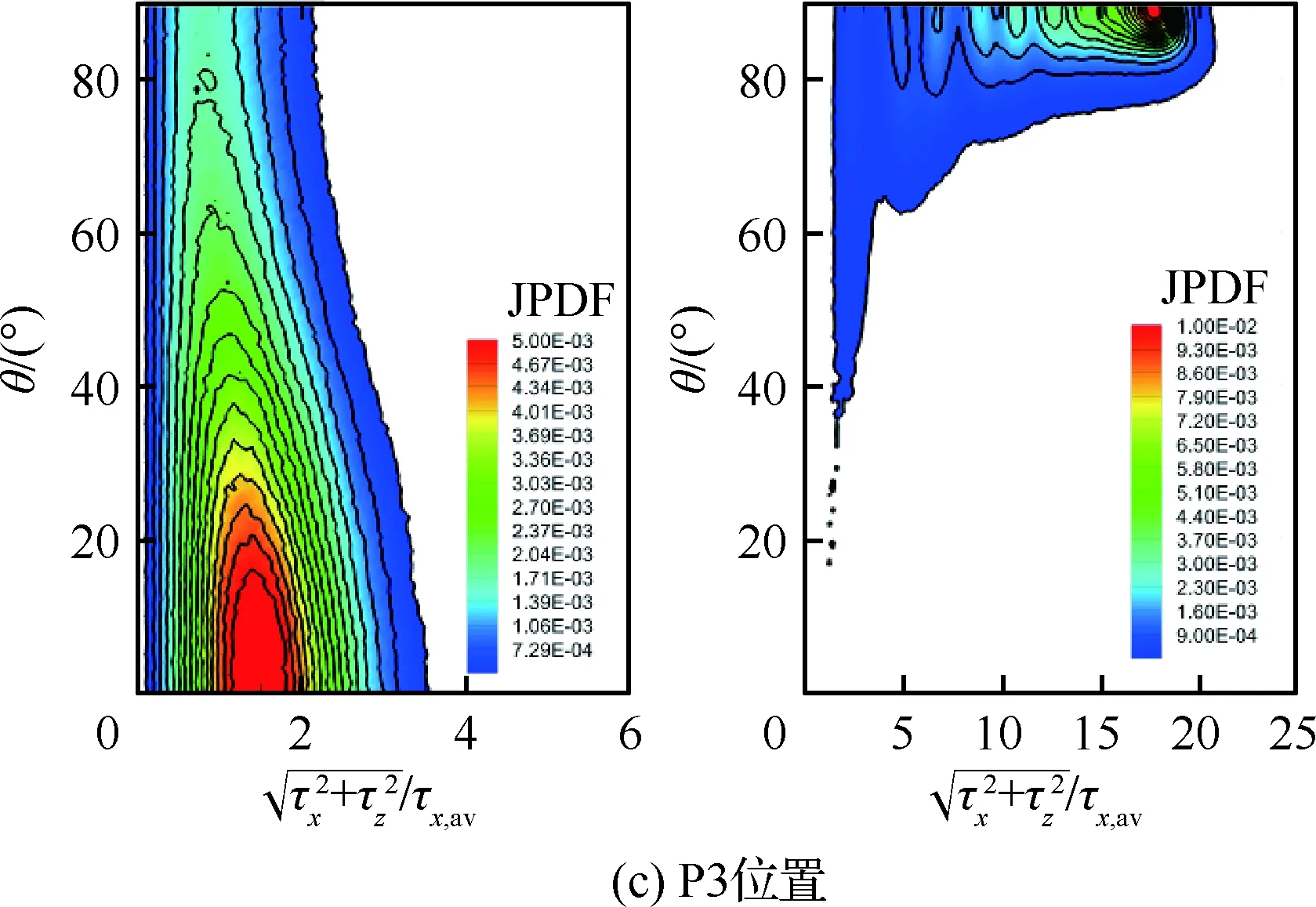
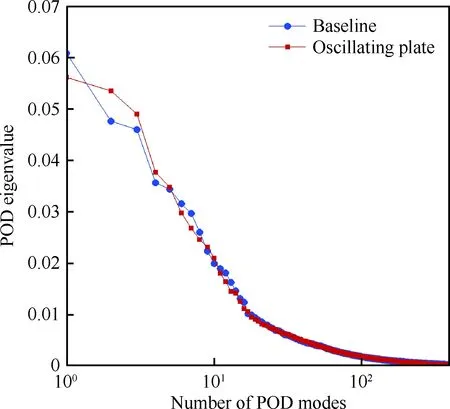
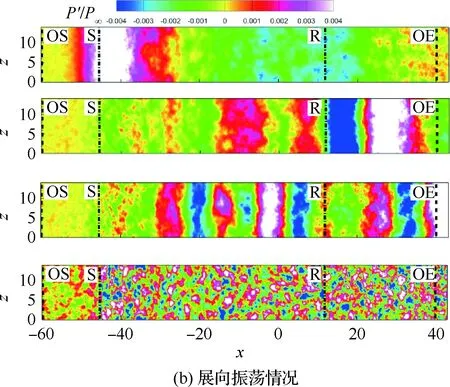
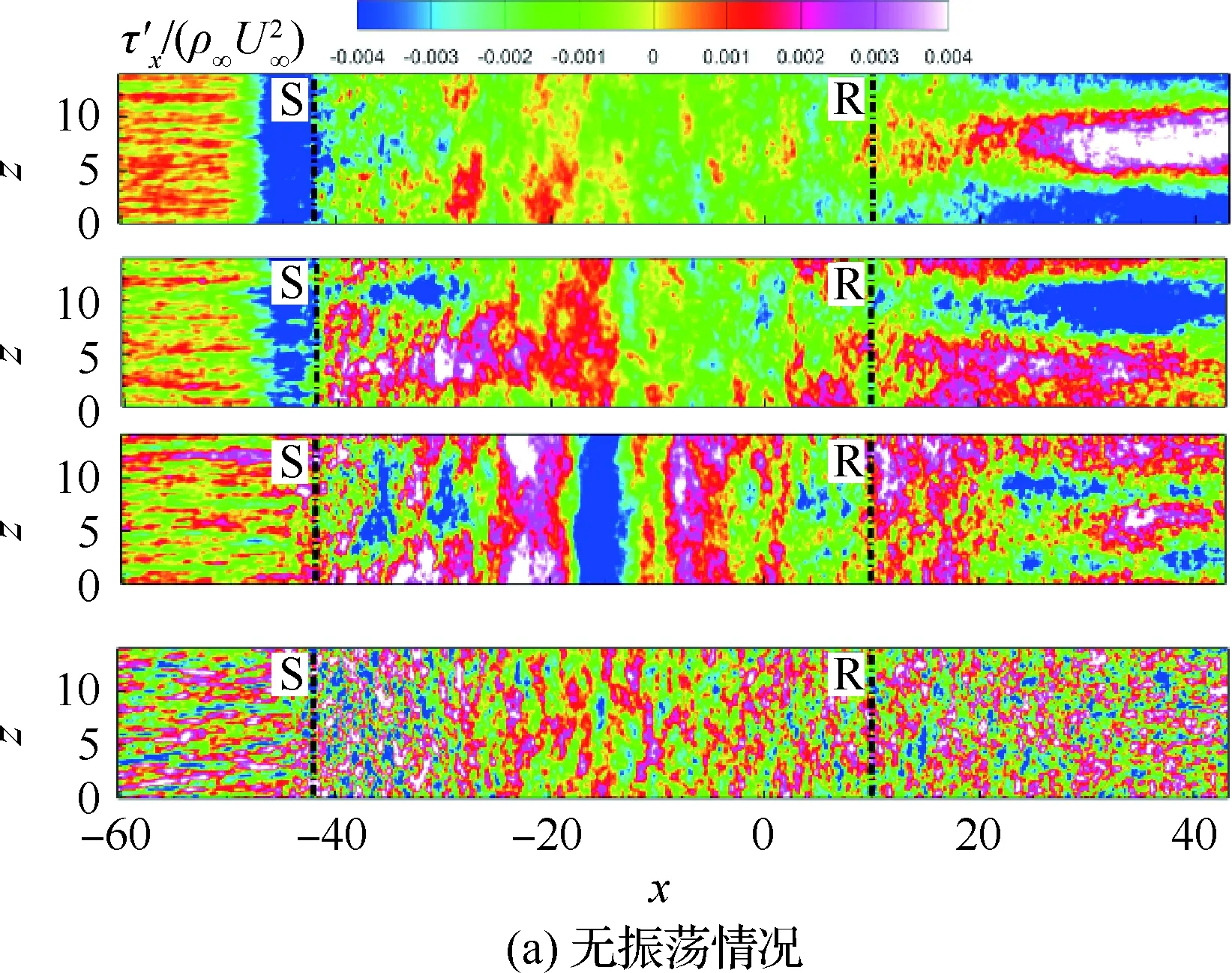
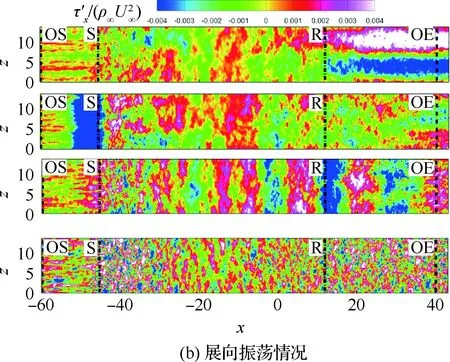
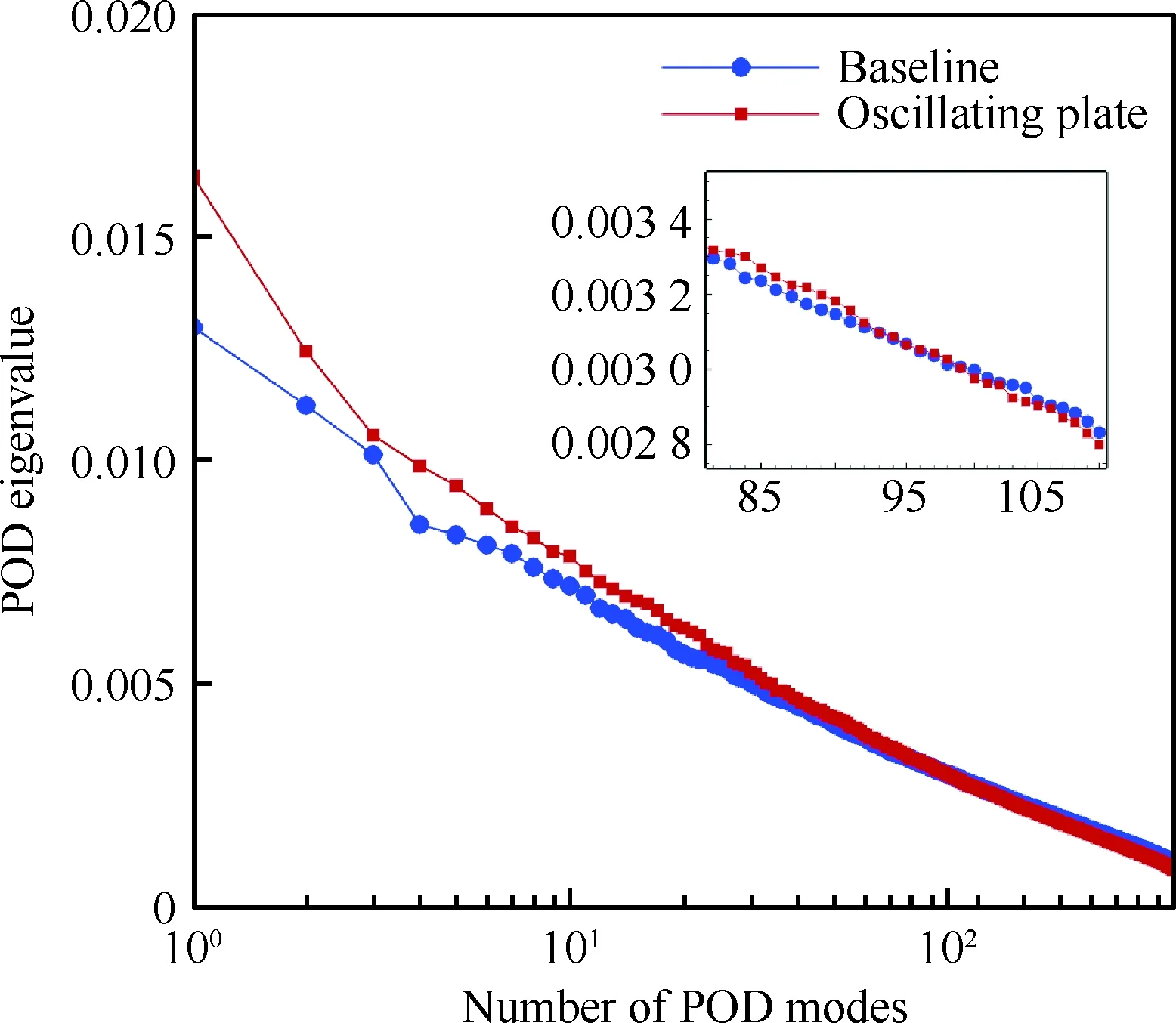
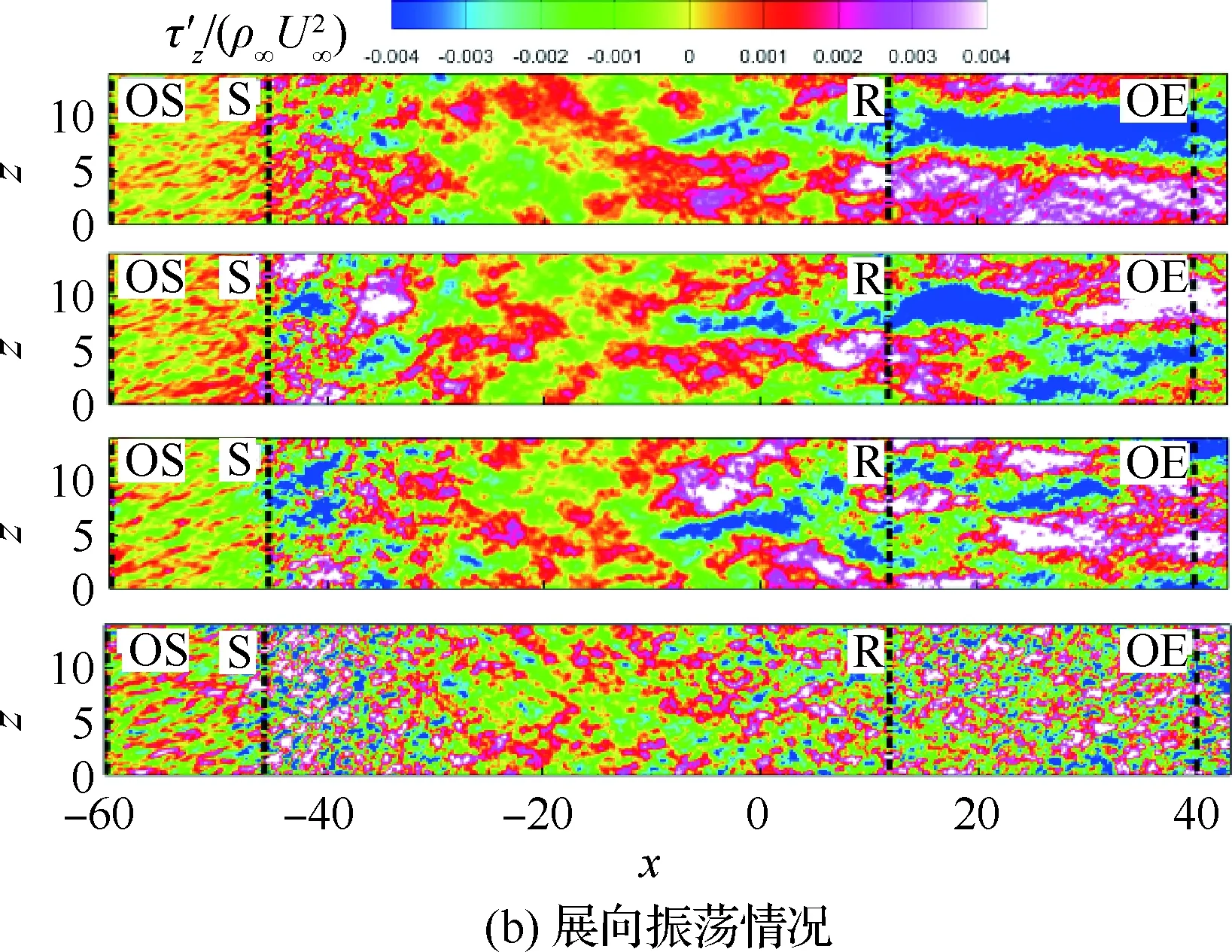
边界条件设置为,进口固定为层流剖面,出口边界采用超声速出口边界,并通过拉伸出口附近的网格以防止出口处产生扰动波干扰内部流场[13]。壁面边界层采用等温无滑移壁面,并且在-335 (3) 式中:Aos=0.5为振荡的幅值;t为无量纲时间;Tos=4为振荡的无量纲周期;xst和xed为振荡开始和结束的流向位置。 图2 湍流边界层统计特性Fig.2 Statistical characteristics of incoming turbulent boundary layer 对于流场结构,首先从激波/边界层干扰的波系结构和分离区结构入手进行研究。在图3中给出了中心截面上无振荡情况以及展向振荡情况下的瞬时密度梯度云图,并用红色实线表示声速线,用蓝色实线表示流向速度为零的等值线以显示非定常分离区。图3结果显示2种情况下波系结构并未发生明显变化,从图中可以较为清楚地分辨入射激波、反射激波、流动再附后形成的再附激波以及其他强度较弱的波系结构。图4给出了展向振荡情况的时间和展向平均的密度场,同样采用红色实线表示声速线,蓝色实线表示分离区大小,并且采用红色虚线和蓝色虚线表示无振荡情况下的声速线和分离区。结果显示平均流场中的波系结构在2种情况下基本是一致的,差别主要体现在分离的位置,存在展向振荡情况下,分离位置更为靠前。进一步计算得到了平均壁面压力和摩阻,并与文献结果进行了比较,如图5所示,图中Pw为壁面压力,并采用无穷远压力P∞进行无量纲化,Cf为摩阻系数,横坐标采用平均分离点xsep和边界层厚度δ进行无量纲化。与无振荡情况相比,压力和摩阻的整体分布十分相似,但是有振荡情况下的分离位置明显提前。这主要是因为展向振荡能够有效降低壁面摩阻[17],进而降低流动抵抗分离的能力。 图3 瞬时密度梯度云图Fig.3 Instantaneous density gradient contours 图4 时间平均密度云图Fig.4 Time-averaged density contours 图5 时间平均的壁面压力和摩阻沿流向分布Fig.5 Time-averaged wall pressure and skin friction coefficient in streamwise direction 图3和图4中瞬时和平均的结果表明壁面的周期振荡对于激波/边界层干扰波系结构和分离区结构的影响并不显著。但本文中所采用的振荡幅值为0.5倍无穷远来流速度,振荡周期为4个无量纲时间,约化频率为St=1.65δ/U∞,明显高于来流湍流的特征频率,如此高的能量输入为何未能有效控制激波干扰的流动分离,是需要进一步探究的问题。首先从分离泡的运动过程入手。激波/边界层干扰引起的分离泡除在流向方向的来回运动外,还可能存在展向运动。在运动运动过程中,必然会涉及到动量大小和方向的改变,为表征分离泡在流向和展向的运动过程,定义如下变量: (4) 以及: (5) 式中:Hx和Hz分别表征的是分离泡内从后往前回流的动量以及展向运动的动量;u(y)和w(y)分别为流向和展向速度;h0为分离泡高度。图4结果显示在x=-15处分离泡的高度最高,下面选取该位置处展向中截面上3个不同的法向高度进行积分。这3个法向高度分别为h1=0.02δ,h2=0.264δ和h3=0.528δ,需要特别指出的是,h3为分离泡内该位置处流向平均速度为零的法向高度。3个位置处的流向回流动量和展向动量的频率(f)加权功率谱密度(PSD:Power Spectral Density)见图6,并采用无穷远速度进行无量纲化。可以看到2种情况下不同积分高度的流向回流动量在频谱上十分类似,频率的峰值位置集中在0.3~0.5附近,在0.05 附近也有少量的频率尖峰,说明展向振荡对于分离泡的流向振荡过程影响较小。而从展向动量的频谱分析上看,两者存在明显差异,特别是在图6(a)中,振荡平板上展向动量的能量主要集中在频率为1.65左右,其他频段范围内的能量较无振荡情况下出现明显降低。该频率为周期振荡的频率,可以看出在壁面附近展向振荡是流动的主要运动状态。而随着法向高度的增加得到改善,周期振荡频率所占有的能量比例快速下降。发生这一现象的原因可能是因为积分是从壁面开始的,而壁面附近振荡平板具有较大的展向速度,导致展向动量在振荡频率附近出现频率峰值,而随着法向高度的增加,振荡平板的影响快速减弱。为证实这一观点,对流场进行相平均,在图7中给出了相位为π/2时展向速度的平均流场以观察展向速度的穿透深度,为对比分析,在图中给出了平均流向速度等于零的等值线(图中黑色实线)以表示分离泡的平均位置,图中y1表示展向振荡的穿透深度,y2表示分离泡的高度。从图6中可以看出,展向振荡的影响局限在壁面附近,没有深入到流场内部,并且在分离前的影响法向高度要略大于分离区内的穿透深度。 图6 x=-15处流向回流动量(左侧)和展向动量(右侧)的加权功率谱密度Fig.6 Power spectral density of streamwise reverse momentum (left) and spanwise momentum (right) at x=-15 在图7中选取了分离前后3个流向位置,在图8中给出了相位为π/2的平均展向速度剖面,并且与Stokes理论解[23]进行比较。Stokes理论解的表达式为 (6) 式中:A为振荡幅值;ω为振荡频率;υ为运动黏性系数。从图8中可以看出,分离区前的湍流边界层的展向速度分布与Stokes的公式符合良好,穿透深度约为分离泡高度的4%。造成分离区内展向速度耗散较快的原因可能是分离泡是以大尺度流动结构为主,并且其中的流体具有相对较低的流动速度,在分离泡内黏性的耗散作用尤为明显,因此展向振动所带来的壁面附近展向速度的变化,会在黏性作用下很快耗散。而在再附之后,边界层会明显增厚,底部低速流体增多同样造成展向速度的快速耗散。 图7 展向速度相平均流场(π/2)和平均流向速度为零的等值线Fig.7 Phase averaged flow field of spanwise velocity (π/2) and contour line of zero average streamwise velocity 图8 不同流向站位上的π/2相位展向速度剖面Fig.8 Spanwise velocity profiles of phase π/2 at multiple streamwise locations 从上面的分析得知,壁面周期振荡的影响仅限于壁面附近的区域。本节将进一步分析展向周期振荡对壁面压力、壁面剪切的统计特性和非定常特征的影响。 图5已经给出了时间和展向平均的壁面压力分布,结果显示在存在振荡情况下,分离稍提前,但整体分布上两种情况下并无明显差异。图9给出了壁面压力的间歇特征。计算方法参考文献[25]。 间歇因子(Intermittency)定义为当地压力值在总时间范围内大于给定阈值Pthres的比例。根据文献[25],Pthres=P∞+4Prms,其中Prms为上游边界层壁面压力的均方根。正如图5所显示分离激波的位置相比无振荡情况较为提前。将间歇因子等于0.1~0.9之间的流向距离定义为间歇长度λ,并在图中进行标注。在存在展向振荡情况下间歇长度为2.84,而无展向振荡情况间歇长度为2.34。由此可见展向振荡会显著增加激波的间隙性,增大间歇长度。 图9 壁面压力间歇因子分布Fig.9 Distribution of intermittency of wall pressure 在对分离泡尺寸变化进行分析后,进一步对其低频特征进行分析。图10给出了分离位置处压力脉动(P′)随时间的变化历程,并给出了对应时间历程的低通滤波结果。采样的时间间隔为tsample=0.024 8U∞/δ,共计16 817个样本,采用时间总长为420.4U∞/δ。在图10中可以看到除高频信号外,2种情况下都能观察到4个较大时间跨度的压力变化周期。 对上述压力信号进行加权功率谱密度(Weighted Power Spectral Density, WPSD)分析,结果如图11所示,可以看到2组信号均存在2个峰值信号。一个是在fδ/U∞=1附近,该峰值信号对应于来流湍流特征频率;另一个是在0.005 图10 分离位置壁面压力脉动的时间历程Fig.10 Time history of wall pressure fluctuation at separation location 图11 分离点壁面压力信号加权功率谱密度Fig.11 Weighted power spectral density of wall pressure at separation location 图12 物面压力加权功率谱密度云图Fig.12 Weithted power spectral density contours of wall pressure 为更加清楚显示低频在整个频率范围内的能量占比情况,将频率0.1以下视为低频,0.1以上为高频,并在不同流向位置处,计算0.1以下频率占总能量的百分比,结果如图13所示。从图中可以看出,在分离之前,低频能量占总能量较低的比重,流动主要以湍流特征频率附近的高频能量为主。在分离位置处,低频能量迅速增加,无振荡情况下低频能量占比可达总能量的60%以上,而在施加振荡之后,低频能量占比降低,为总能量额40%。经过分离后,低频能量逐渐降低;在再附位置处低频能量重新升高,达到总能量的20%,并且再附之后一定的流向距离内,低频的能量仍能维持在这一比例左右。 图13 低频运动所占能量百分比Fig.13 Percent of energy of low-frequency motion 3.1节的分析表明展向振荡能够增大分离位置间歇区长度,并且降低分离位置处低频的能量占比。下面对展向振荡对表面摩阻的影响进行分析。在图14中给出了P1~P3流向位置上(具体位置如图7所示)流向摩阻τx和展向摩阻τz之间夹角Ψτ的概率密度分布。夹角Ψτ概率密度的表达式为 (7) 式中:PF(θ)表示事件夹角Ψτ小于θ的概率。类似地还给出联合概率密度的表达式: (8) 其中:JPF(θ,τ)表示事件夹角Ψτ小于θ且物面剪切应力小于τ的联合概率。 图14 物面切应力夹角概率密度函数分布Fig.14 Probability density functions of angle between wall shear stress components 图15 物面切应力夹角与切应力幅值联合概率密度分布(左侧:无振荡情况,右侧:振荡情况)Fig.15 Joint probability density functions of angle and magnitude of wall shear stress vector (left: baseline, right: oscillating plate) 在图14的分析中已经指出,在壁面振荡时展向切应力占主导,概率密度的峰值出现在夹角80°以上。这与图15中振荡平板的联合概率分布结果一致。并且还发现在振荡情况下,概率密度分布会出现多个极大值点。这主要是由于振荡速度呈正弦分布,导致展向切应力的分布也与正弦型类似,故会出现离散的多个概率密度极大值。 为进一步研究周期振荡对物面压力和剪切力非定常特性的影响,本节采用本征正交分解(POD)对物面压力脉动、脉动流向摩阻和展向摩阻进行了模态分解,共选择了401个瞬像,瞬像的间隔时间为8个无量纲时间。 图16中给出了表面脉动压力POD分解得到的特征值,而特征值的大小表示POD模态所对应的相对能量大小。可以看到2种情况下,能量在主要模态之间的占比存在较大差异,在振荡情况下,模态1~模态3的能量占比分别为5.6%、5.3%和4.8%,而无振荡情况下模态1~模态3的能量占比为:6.0%、4.7%和4.5%,可见存在振荡情况下,模态1的能量降低,模态2和模态3的能量升高。在模态15以后,2种情况下高模态的能量分布十分接近。 图17中给出了脉动压力POD模态的空间分布,左侧为无振动情况,右侧为振动情况,从上至下依次为第1模态、第3模态、第9模态和第15模态。从第1模态上看,无振荡情况下,在分离位置和再附位置均有较高的能量;而存在振荡情况下,能量主要集中在分离区附近,再附位置的能量较低。从第3模态上看,无振荡情况下,在分离位置上仍有较高的能量,并且在分离泡内的能量也比较高;而在存在振荡的情况,分离位置没有明显的能量,在分离泡和再附位置上具有较高的能量。2种情况的第9模态能量分布十分相似,只是分离位置略有不同。第15模态对应小尺度的流动结构,2种情况第15模态能量分布基本一致。 图16 壁面压力脉动的POD模态能量Fig.16 Normalized energy of POD modes of wall pressure fluctuations 图17 物面脉动压力POD模态的空间分布(从上至下:第1模态、第3模态、第9模态和第15模态)Fig.17 Spatial distribution of POD modes of wall pressure fluctuations (from top to bottom: Mode 1, Mode 3, Mode 9 and Mode 15) 图18给出了流向剪切脉动的POD模态能量分布。与脉动压力类似,2种情况的主要模态能量存在明显差异。在振荡情况下,模态1~模态3所占的能量分别为:2.3%、2.2%和1.5%,而无振荡情况下能量为 2.8%、1.8%和1.4%,可以看到与压力脉动的POD分析结果类似:存在振荡时,流向摩阻的POD模态能量会发生从模态1向模态2和模态3的转化,并且在模态3之后,2种情况的POD模态能量差异变得很小。 图19给出了壁面流向剪切脉动(τ′x)的POD模态空间分布。从第1模态看,无振荡情况下,在分离位置和再附后都有较高的能量,并且在再附后出现较大尺度的流向结构,沿展向呈现极大值和极小值交替分布的形式;存在振荡时,在分离区位置处没有较高的能量,而在再附后与Görtler涡结构相关的模态上拥有较高的能量,并且Görtler涡的流向尺寸也明显较无振荡情况大。从第3模态的空间分布上看,无振荡情况下在再附区后仍有较为清楚的流向结构;有振荡情况下,在分离位置出现较高的能量,而在再附后原来的流向涡结构则并不明显,有可能是第1模态~第3模态之间的能量转移导致了再附后模态结构的变化。从第9模态和第15模态的空间分布上看,2种情况并未出现较为明显的差异,这与图18中的能量分布情况是一致的,在第3模态之后,2种情况的POD模态之间的能量相差不大,预示着所表征的流动结构也是十分类似的。 图18 壁面流向剪切脉动的POD模态能量Fig.18 Normalized energy of POD modes of wall streamwise shear fluctuations 图20给出了壁面展向剪切脉动(τ′z)的POD模态能量分布。在振荡情况下,模态1~模态3分别为:1.6%、1.2%和1.0%,而无振荡情况下模态1~模态3的能量占比为 1.3%、1.1%和1.0%。 从图中可以发现,与壁面压力脉动和流向剪切脉动的POD模态有较大不同的是,在振荡情况下,POD模态的能量占比要比无振荡情况高,且这一趋势一直持续到第95模态左右,该模态对应的流动结构已经是小尺度流动结构。这可能是由于壁面展向振荡影响展向剪切,提高了展向剪切的能量。图21给出了展向剪切脉动POD模态的空间分布。整体而言,2种情况下,展向剪切脉动的POD模态的空间分布是十分相似的;但在有振荡情况下,再附后的流动结构相比无振荡情况略有增加,这也与图20中能量模态的分布规律较为一致。 图19 壁面流向剪切脉动POD模态空间分布(从上至下:第1模态、第3模态、第9模态和第15模态)Fig.19 Spatial distribution of POD modes of wall streamwise shear fluctuations (from top to bottom: Mode 1, Mode 3, Mode 9 and Mode 15) 图20 壁面展向剪切脉动的POD模态能量Fig.20 Normalized energy of POD modes of wall spanwise shear fluctuations 图21 壁面展向剪切脉动POD模态空间分布(从上至下:第1模态、第3模态、第9模态和第15模态)Fig.21 Spatial distribution of POD modes of wall spanwise shear fluctuations (from top to bottom: Mode 1, Mode 3, Mode 9 and Mode 15) 本文对壁面强展向振荡的入射斜激波/湍流边界层干扰开展了直接数值模拟研究,综合本文分析,可得到如下结论: 1) 在流动结构方面,壁面的展向振荡使壁面摩阻减小,降低了流动抵抗分离的能力,从而导致分离位置提前,分离位置附近的间歇区长度增大。但另一方面,由于展向振荡的穿透深度仅约为分离泡高度的4%,在边界层内黏性耗散作用下,不会影响更高位置处的流场。 2) 在非定常性和统计特征方面,壁面的展向振荡对激波/边界层干扰的低频运动频率影响不大,但会显著降低低频运动的能量占比。无振荡情况下低频能量占比可达总能量的60%以上;而在施加振荡之后,低频能量占比降低为总能量的40%。展向振荡所带来的展向速度在壁面附近远大于流向速度,使得剪切力夹角的概率密度峰值从0°偏移到80°~90°附近。 3) 在POD能量模态方面,POD模态所表征的流动结构具有一定的相似性,但壁面展向振荡会影响POD主要模态之间的能量分布,使能量从低阶模态向高阶模态转移,特别是展向剪切脉动的POD模态这一趋势尤为明显。POD模态分布显示振荡情况下再附后的类Görtler涡结构出现了明显增强。 结合上述结论可以看出,展向强振荡对激波/边界层干扰的整体流动结构不会有明显的影响,但它能够调节能量从低阶模态向高阶模态转移,从而显著降低低频运动的能量占比,对激波的低频运动具有较强的抑制效果。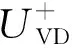
2 展向振荡对流场结构的影响

3 展向振荡对壁面脉动量的影响
3.1 壁面压力脉动
3.2 壁面剪切脉动
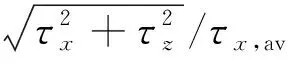
4 本征正交分解
4.1 壁面压力脉动
4.2 壁面流向剪切脉动

4.3 壁面展向剪切脉动

5 结 论
