基于改进粒子群算法辨识Volterra级数的目标机动轨迹预测
2020-12-29奚之飞徐安寇英信李战武杨爱武
奚之飞,徐安,寇英信,李战武,杨爱武
空军工程大学 航空工程学院,西安 710038
轨迹预测是根据目标的历史运动轨迹,学习和推理其包含的内在信息,进而对目标未来的运动趋势作出合理推测的过程。在空空对抗作战过程中,对敌方目标的机动轨迹作出合理的预测具有重要意义。基于包伊德循环(Observe、Orientation、Decide and Act,OODA)理论可知,空战取胜的关键是先敌形成OODA环,从而对敌实现“先敌发现”“先敌调整”“先敌决策”以及“先敌攻击”,达到先发制人的目的[1],实现这一系列行为的基础是对目标机动轨迹实现精确预测,故研究目标机动轨迹预测具有重要意义。
近几年,对于目标机动轨迹预测方法的研究方向主要分为两大类。一类是侧重于卡尔曼滤波算法的传统预测方法。卡尔曼滤波算法能够对目标的运动状态进行最优估计并且能够实现实时状态估计和预测,适用于有限维度的线性和非线性的目标时空运动轨迹。例如文献[2]针对目标运动模式变化多以及机动幅度较大的情况,提出一种基于多项式卡尔曼滤波的运动轨迹预测算法;文献[3]针对历史位置信息存在缺失的情况,提出一种具有系统噪声估计的改进卡尔曼滤波算法对目标机动轨迹进行预测;文献[4]针对传统轨迹预测算法已无法满足高精度和实时性预测要求,提出一种基于卡尔曼滤波的动态轨迹预测算法;文献[5]针对精确高阶目标运动模型存在的高度非线性,数据处理难度大以及预测精度低等问题,提出一种改进的交互多模型轨迹预测算法。上述预测算法都只适用于目标运动特性相对简单的轨迹预测问题,但是在空战过程中,目标的运动往往是高度复杂的时序过程,传统的轨迹预测算法不能准确地学习目标的机动特性,同时也存在建模复杂度高和算法的适应性差的问题,且卡尔曼滤波算法的状态和测量方程的推导很困难,算法的预测精度也不能满足空战对抗需求。
另一类研究方向主要以神经网络算法为主的人工智能算法,结合大数据建立目标机动轨迹预测模型。例如文献[6]利用广义回归神经网络(Generalized Regression Neural Network,GRNN)良好的非线性映射能力以及高度的容错性和鲁棒性,提出一种基于GRNN的高超声速飞行器轨迹预测算法;针对前馈(Back Propagation,BP)神经网络存在对初值敏感且全局搜索能力较差的问题,文献[7-8]分别提出一种基于遗传算法和粒子群算法优化BP神经网络的预测模型。但是,文献[9]提出目标机动轨迹预测问题本质上是动态数据的时间序列预测,具有高度的非线性和时变特性,而传统的BP神经网络是一种静态的单层前馈神经网络,对于不断变化的非线性目标机动轨迹时间序列的预测效果相对较差,同时BP神经网络还存在易陷入极值和过拟合的问题,因而将神经网络应用于目标机动轨迹预测的效果较差。此外,基于神经网络的预测方法需要预先建立时间序列的主观预测模型,确定模型的输入输出以及隐含层结构,然后根据建立的主观预测模型进行计算及预测。随着混沌理论的发展,可不必预先建立主观预测模型,而是基于样本数据时间序列本身所蕴含的客观规律进行预测,这样完全可以避免人为主观性对预测结果造成的影响,从而提高了预测精度和可信度。根据混沌理论,对于某一混沌系统来说,可采用混沌预测模型来进行预测,并且能够获得较高的预测精度。因此,本文引入混沌理论的方法来对目标机动轨迹进行建模和预测。基于上述预测思想,首要需要确定目标机动轨迹时间序列是否具有混沌特性。
近些年,混沌时间序列建模及预测已经成为混沌研究领域中的热点研究方向。目前,基于混沌理论对风功率的研究较多,但是针对基于混沌时间序列建模进行目标机动轨迹预测的研究尚未出现。由混沌理论可知,混沌信号经过相空间重构之后,会得到一个嵌入空间的低维流形,利用其可对重构的时间序列进行预测[10]。此外,Volterra级数预测模型是近些年发展起来的一种预测模型[11],理论和实践表明,Volterra级数模型可以很好地表征非线性系统,可以对任何非线性函数进行逼近,并且能够对混沌吸引子的轨迹进行跟踪,可实现对未来变化趋势的精确预测。为了更好地处理目标机动轨迹存在的非线性和时变特性,将Volterra级数模型引入到目标机动轨迹时间序列预测中,从而实现对目标未来机动轨迹的精确预测。利用Volterra泛函级数模型进行目标机动轨迹预测的关键在于辨识其核函数,然而,Volterra级数核函数辨识存在一个难点,即核参数的数量随着Volterra级数核阶数呈指数增长,计算困难。目前Volterra泛函级数参数辨识的方法主要有最小二乘算法[12-13]、最小均方(Least Mean Square,LMS)算法、递归最小二乘法(Recursive Least Square,RLS)以及智能启发式优化算法[14-18],但是,最小二乘法在辨识参数时要求目标函数连续可导,且采用梯度信息进行搜索时容易陷入局部极值;基于LMS和RLS的全耦合和部分耦合确定Volterra级数核参数的算法收敛性、稳定性以及辨识有效性都不是很好。上述这些传统算法都存在计算复杂、辨识精度低以及算法收敛速度慢等不足。为了克服传统算法存在的不足,本文采用仿生智能算法辨识Volterra级数核参数。
粒子群算法是一种模拟生物行为的群智能优化算法[19-20],具有结构简单且易于实现、容易收敛且鲁棒性较强的优点[21]。粒子群算法为求解复杂系统优化问题提供了一种通用框架,该算法不依赖于问题的具体领域,对问题的种类适应性很强,而Volterra级数核函数辨识实质上是一个高维度参数优化问题,因此,本文将粒子群算法引入到Volterra泛函级数模型的核函数参数辨识中,该算法不仅可以避免传统算法要求待优化函数必须满足连续可导的缺点,还可以得到很好的优化效果和鲁棒性。
文献[22]通过研究发现,基于基本的粒子群算法对Volterra级数核函数进行辨识时,在算法搜索后期,粒子容易聚集,导致算法容易陷入最优解;同时,对于Volterra级数核函数进行辨识是一个高维度优化问题,粒子群算法在优化高维度问题时,容易出现早熟现象,导致算法陷入局部最优而无法跳出,同时还存在收敛精度不高的问题[23]。基于上述分析,为了同时提高算法的优化性能和避免陷入局部极值点,本文引入一种基于混沌变异和自适应策略优化的粒子群算法,并将改进的粒子群算法(Modified Particle Swarm Optimization algorithm,MPSO)用于Volterra泛函模型参数辨识,构建一种基于改进粒子群算法辨识的Volterra级数目标机动轨迹预测模型。通过仿真实验,该模型的预测性能优于基于标准粒子群算法、遗传算法、蚁群算法辨识的Volterra级数预测模型,同时也验证了该预测算法的有效性和鲁棒性。
1 混沌特性分析及相空间重构
1.1 混沌特性分析
检验时间序列是否具有混沌特性的算法主要有最大Lyapunov指数法、G-P(Grassberger-Procaccia)算法以及0-1检测法等。最大Lyapunov指数法在确定时间序列是否具有混沌特性时,需要预先计算时间序列的平均最大周期、嵌入维数和延迟时间,目前确定每一个参数的算法有很多种,但是不同的方法得到的参数并不一致,由于缺乏相应的客观评判依据,对于参数选择难度较大,同时算法的计算复杂度高,实时性差;G-P算法通过估算出数据的关联维数来判定时间序列的混沌特性,该算法容易受到时间序列长度和数据噪声的影响,随机噪声也会对其造成一定的影响,故判读结果可信程度不高。0-1检测法不需要确定相空间重构参数,直接输入离散时间序列即可,不需要预先确定其他参数,最后通过算法返回的数值趋近于0和1来判定输入时间序列是否具有混沌特性,同时,0-1检测法适用于含有噪声时间序列,且计算量小,所需时间短,可以实现快速判断时间序列的混沌性。
本文主要借鉴0-1检测法[24-25]对目标机动轨迹时间序列x(n)∈{x(1),x(2), …,x(N)}进行混沌特性判定,此算法不需要对时间序列进行相空间重构预处理,可以直接对时间序列进行混沌特性检测,算法具体流程如下:
1) 计算平移变量pc(n)和qc(n),即
(1)
(2)
式中:n=1, 2, …,N;c∈(0,π)。
2) 计算变量pc(n)和qc(n)的均方位移Mc(n),即
[qc(i+n)-qc(i)]2}
(3)
3) 根据均方位移计算渐进增长率Kc,即
(4)
4) 重复步骤1)~3),循环计算时间序列的均值K。
时间序列混沌特性判定的准则是:当均值满足K≈1时,则说明该时间序列具有混沌特性;当均值满足K≈0,则说明该时间序列不具有混沌特性。本文通过仿真计算得到目标机动轨迹的三维坐标时间序列的均值K分别为KX=0.998 1,KY=0.986 7,KZ=0.963 4。基于判定准则可知,目标机动轨迹的三维坐标时间序列均具有混沌特性。
1.2 相空间重构
相空间重构是分析混沌时间序列的关键环节,能够挖掘出时间序列中所蕴含的信息,根据Takens嵌入延迟定理[26],选择合适的时间延迟τ和相空间重构嵌入维数m可以获得与原系统具有相同的动态特性的新系统。对一维时间序列x(n)进行相空间重构,得到的多维时间序列为
(5)
则相空间重构之后多维空间的相点数Np为
Np=N-(m-1)τ
(6)
1.3 基于改进C-C法确定相空间重构参数
在对混沌时间序列进行分析时,时间延迟和嵌入维数的确定,直接关系到能否充分反映原始时间序列的特性变化[27]。针对传统C-C法在求解时间延迟和嵌入维度存在的不足,本文采用改进的C-C法[28]来确定相空间重构相关参数,使得计算结果更加准确。
定义关联积分为
(7)
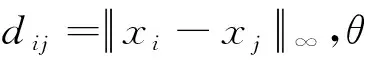
定义检验统计量为
S1(m,N,r,τ)=C(m,N,r,τ)-Cm(1,N,r,τ)
(8)
在计算检验统计量时,采用划分子时间序列的计算方法,即
S2(m,N,r,τ)=
(9)
定义差量为:
ΔS(m,N,r,τ)=
max{S(m,N,r,τ)}-min{S(m,N,r,τ)}
(10)

(11)
(12)
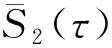
m=τw/τ+1
(13)
2 Volterra级数模型
对于输入为x(k)和输出为y(k)的离散时间非线性动态系统,通过Volterra级数模型可将其描述为[29]
(14)
(15)
式中:e(k)为Volterra级数截断误差;hn(m1,m2,…,mn)为非线性系统的n阶Volterra级数核函数,核函数具有对称性且对称性是唯一的[29]。在确定Volterra级数核函数的过程中,充分利用其对称性可以大大减小Volterra级数模型的计算量。
利用截断的Volerra级数可以精确近似描述很多非线性系统,在对非线性进行描述时,一般采取前三阶的截断形式,故通常是对Volterra级数模型的前三阶核函数进行辨识[29]。根据Volterra级数核函数所具备的对称特性以及Volterra级数表达形式,可将系统的输出表达为
h2(m1,m2)x(k-m1)x(k-m2)+
x(k-m1)x(k-m2)x(k-m3)+e(k)
(16)
式中:Mi为模型的记忆长度,当Mi取合适的值时,截断误差e(k)可以充分小,在误差允许的范围内,e(k)可以忽略不计;s1(m1)、s2(m1、m2)、s3(m1、m2、m3)由式(17)~式(19)确定:
s1(m1)=1
(17)
(18)
s3(m1,m2,m3)=
(19)
假设Volterra级数模型截断的最高阶数为NT,假设系统的输入矩阵为
P=[X(k),X(k+1), …,X(k+L-1)]T
(20)
式中:L为输入数据的长度。则k时刻的截断Volterra级数系统输入向量可表示为
X(k)=[x(k),x(k-1),…,x(k-M1+1),
x2(k),x(k)x(k-1), …,
xN(k-MNT+1) ]T
(21)
此时,截断Volterra级数系统输出向量以及核函数可表示为
Y=[y(k),y(k+1),…,y(k+L-1)]T
(22)
H=[h1(0),h1(1),…,h1(M1-1),h2(0,0),
h2(0,1), …,hN(MN-1, …,MN-1)]T
(23)
式中:X(k)为输入向量;Y为输出向量;H为Volterra级数的核函数。基于上述表达可将系统表述为
Y=PH+e
(24)
式中:e为误差。由式(24)可知,基于截断Volterra级数模型的非线性系统辨识,就是在确定的系统输入和输出的基础上确定Volterra级数的核函数向量H。Volterra级数系统辨识实际上是一个最优化参数估计问题,本文采取一种基于混沌变异和自适应策略优化的粒子群算法来解算Volterra级数核函数向量。
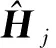
(25)
式中:L为数据长度,j=1, 2, …,n。对于粒子群中第j个粒子的速度和位置进化规则为
vj(t+1)=ωj(t)vj(t)+
(26)
(27)
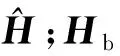
改进的粒子群算法在寻优的过程中,通过不断搜索寻找使得式(27)所示的目标函数值最小的全局最优位置,即Volterra级数核矢量的最佳辨识结果。
3 基于改进粒子群算法辨识的Volterra级数预测模型
3.1 改进的粒子群算法
通过对文献中粒子群算法研究发现,目前大多数的文献未能充分发挥粒子群算法的优良性能,也未能充分考虑粒子群算法的性能与算法进程之间的关系,从而在一定程度影响了算法的收敛速度和寻优效率;同时,在算法的寻优过程中由于粒子群存在容易聚集的特点,种群的多样性难免会降低,因而可能会导致算法存在容易陷入局部极值、早熟的不足。
针对目前粒子群算法存在的不足,本文主要从3个方面来改进基本的粒子群算法:
1) 利用混沌具有的良好的随机性、便利性以及规律性等特点,对粒子群进行初始化操作。
2) 依据粒子群的进化进程的不同,采取不同的算法来改进粒子群算法,在进化的过程中将粒子群划分为精英子种群和普通子种群,同时对各个子种群采取不同的参数自适应调整策略,从而达到增加种群多样性、实现全局和局部搜索能力相平衡的效果。
3) 为了更好地发挥粒子群算法的寻优性能,实时判断算法是否陷入局部最优解,当算法陷入局部最优解时对粒子进行混沌变异操作。
3.1.1 基于混沌映射初始化粒子群
在不改变粒子群算法随机初始化时所具有的良好性能前提下,采用混沌映射对粒子群进行初始化,混沌映射可以有效地提高粒子种群的多样性。文献[30-32]通过对比分析得出Tent映射模型比Logisitic映射模型具有更高的搜索效率的结论,同时也验证了Tent映射可以更好地改善粒子群的多样性以及算法的寻优能力。本文采用Skew-Tent映射模型对粒子群进行初始化操作,具体的Skew-Tent混沌映射模型为
xk+1=g(xk)
(28)
(29)
式中,当参数φ在[0,1]取值,并且x∈[0,1]时,式(25)和式(26)所描述的系统处于混沌转态。利用Skew-Tent混沌映射对粒子群进行初始化的具体流程如算法1所示。

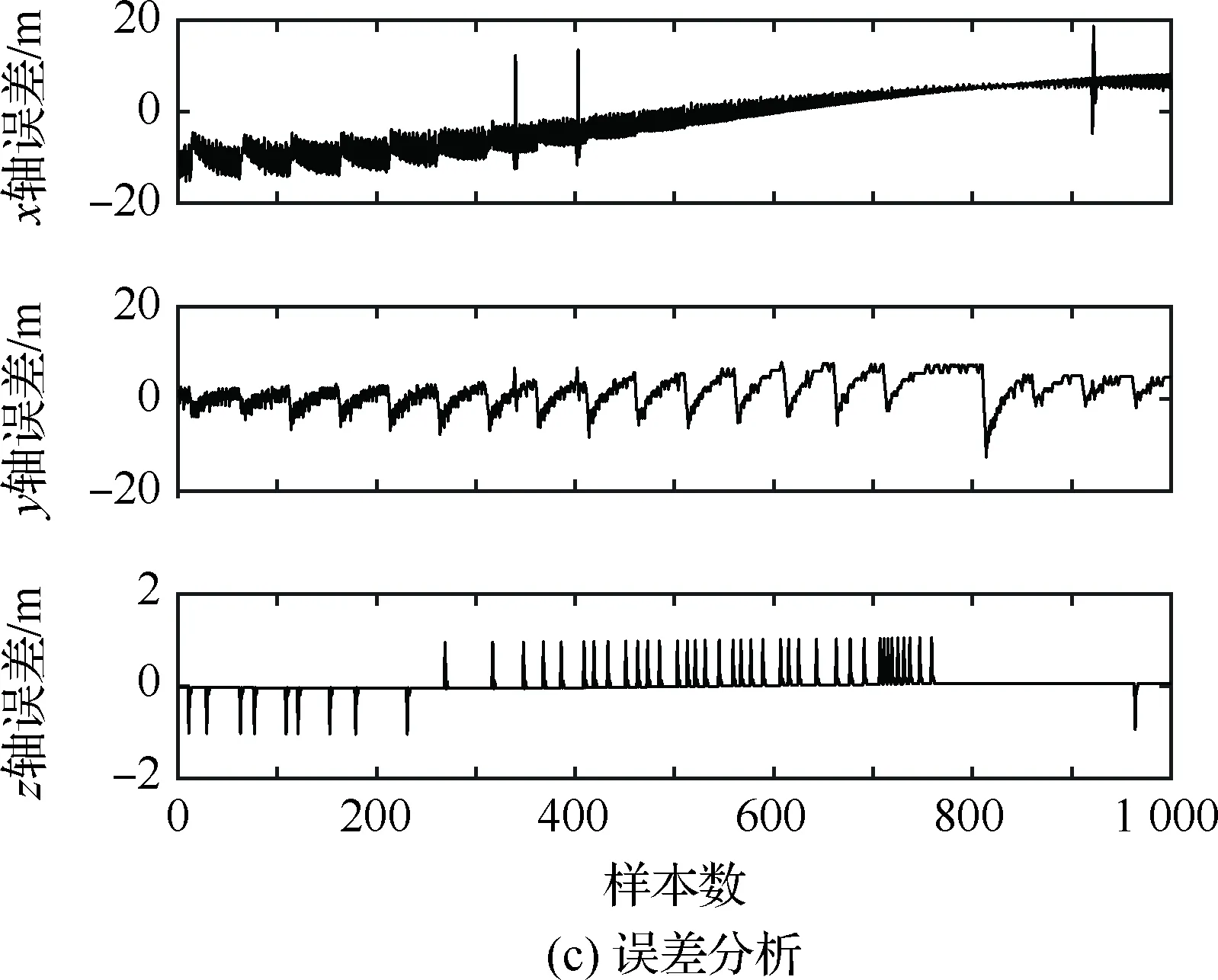
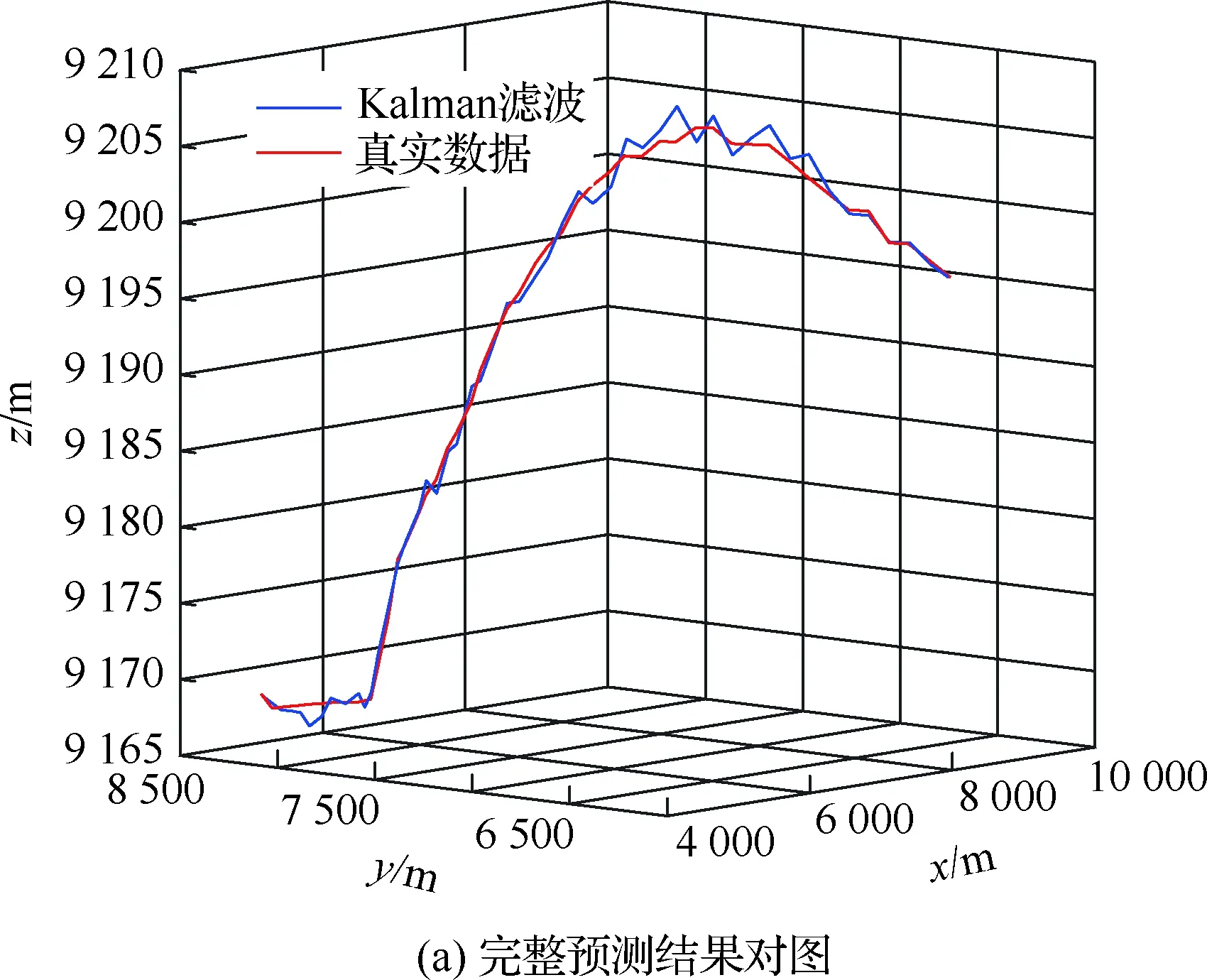
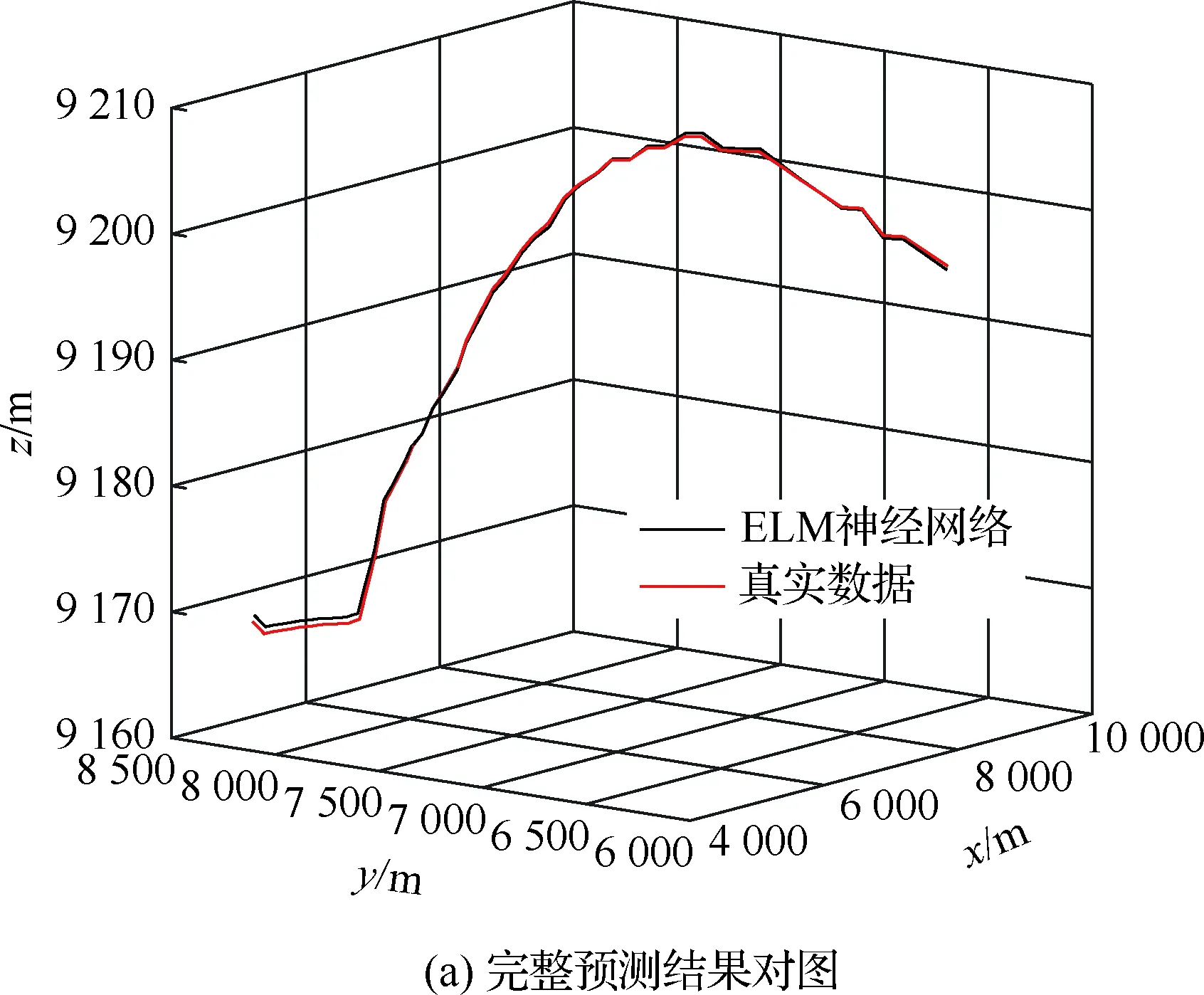
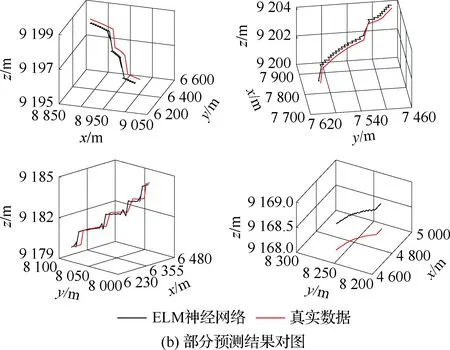
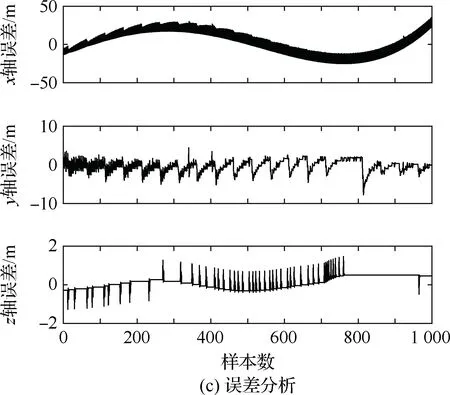
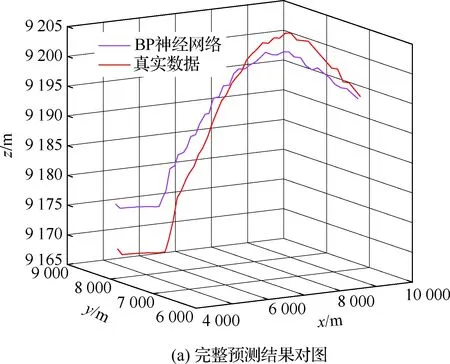
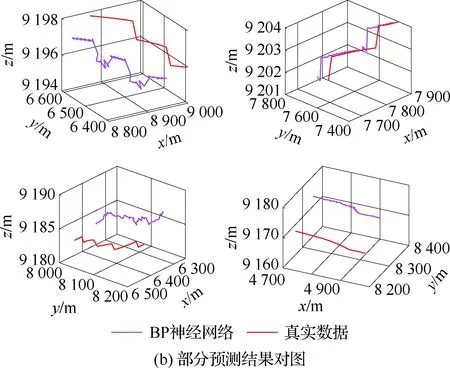
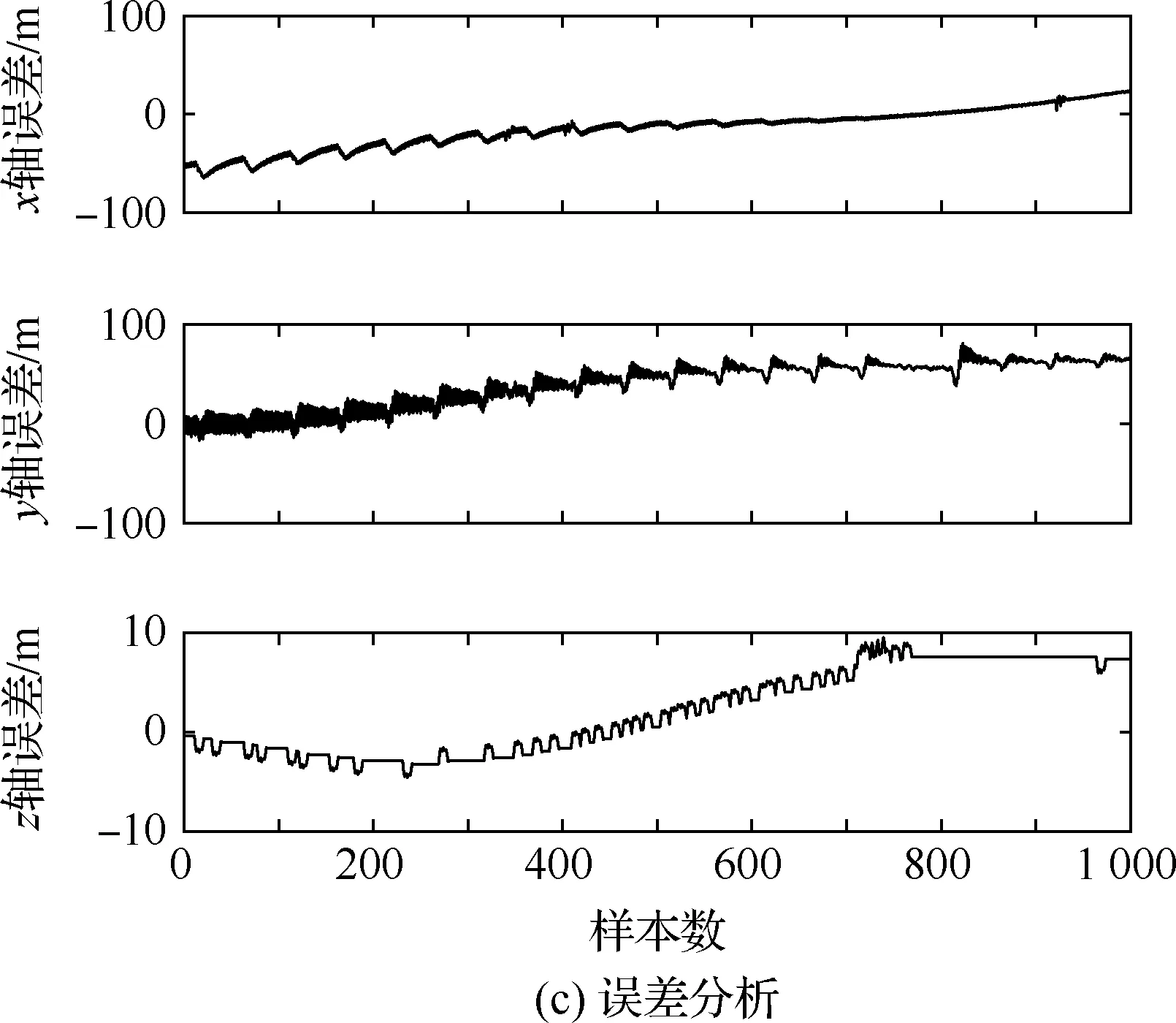
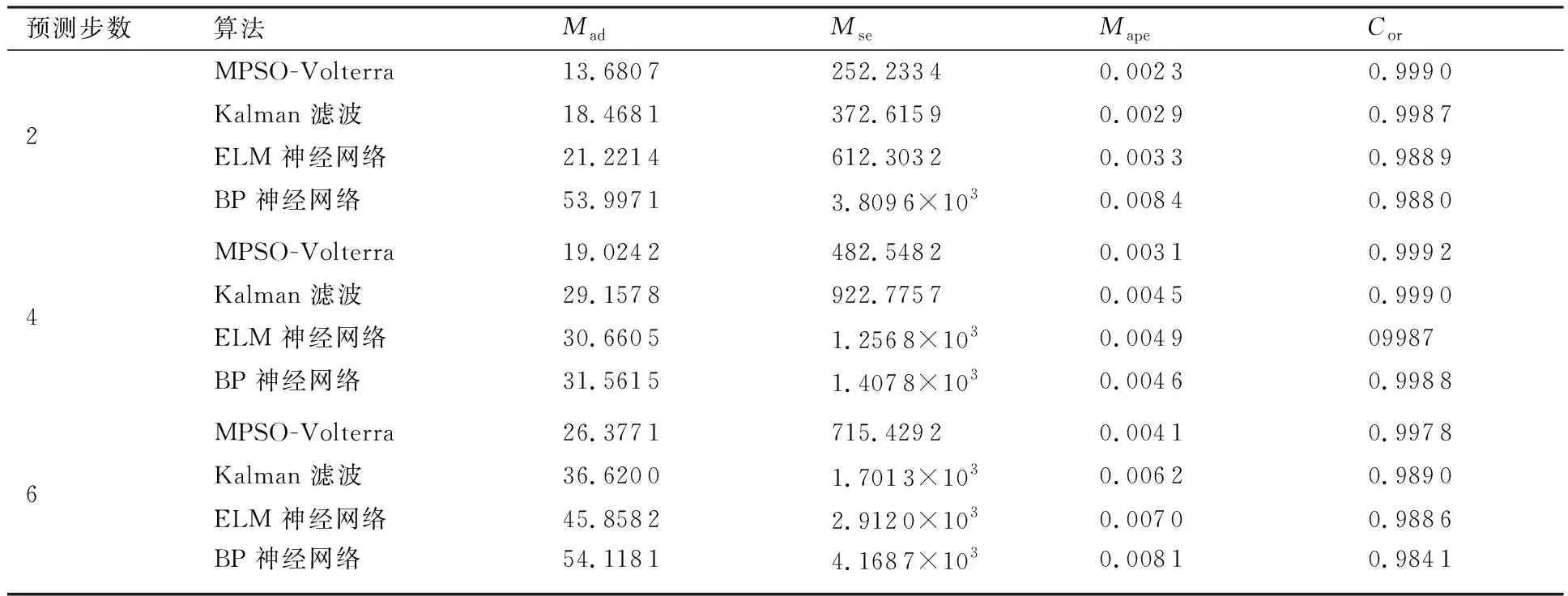
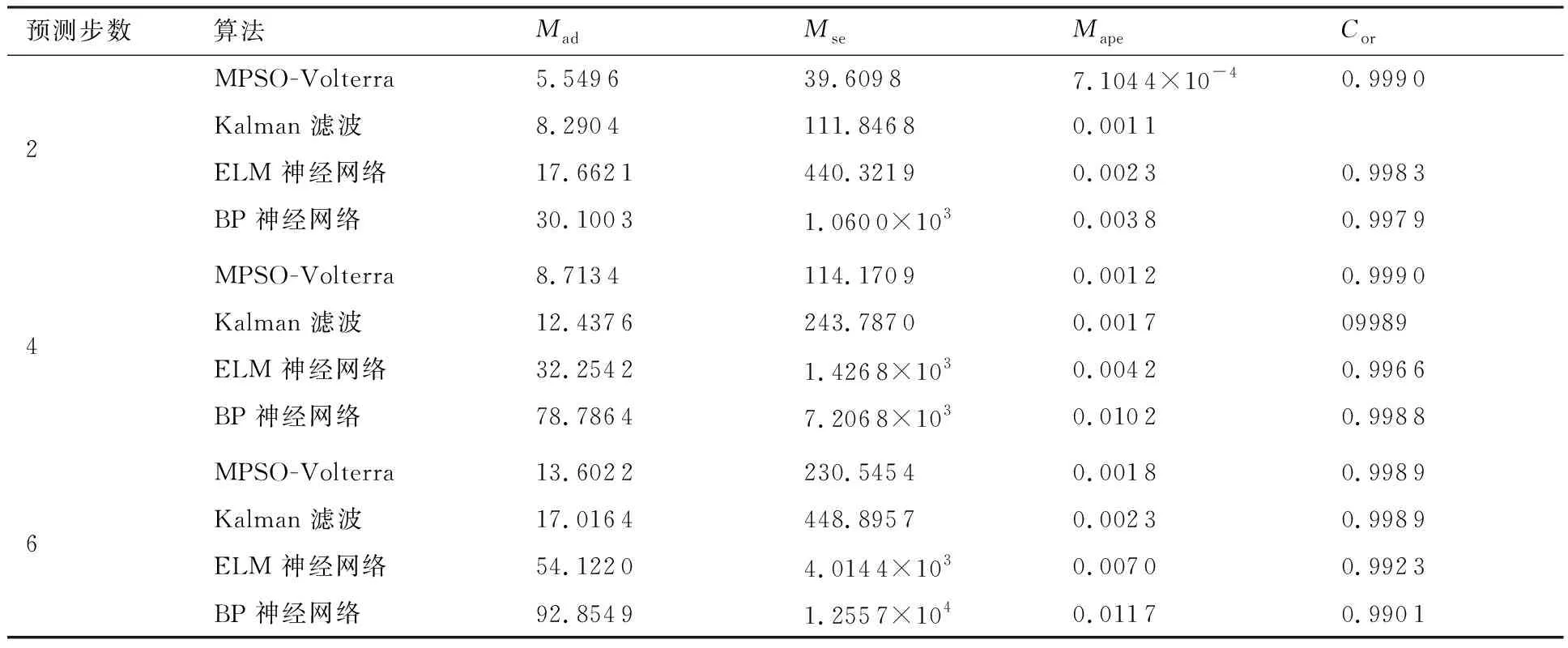
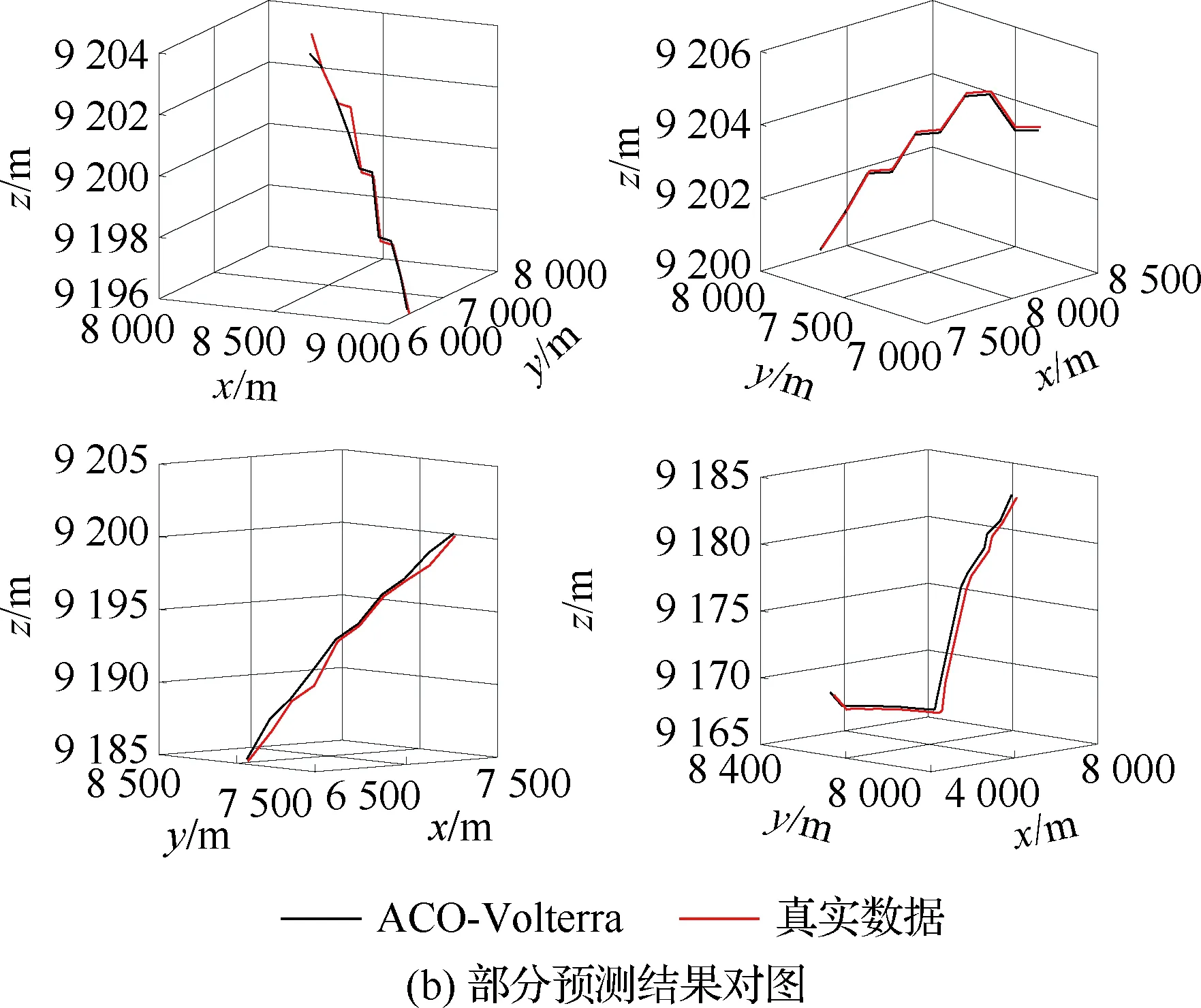
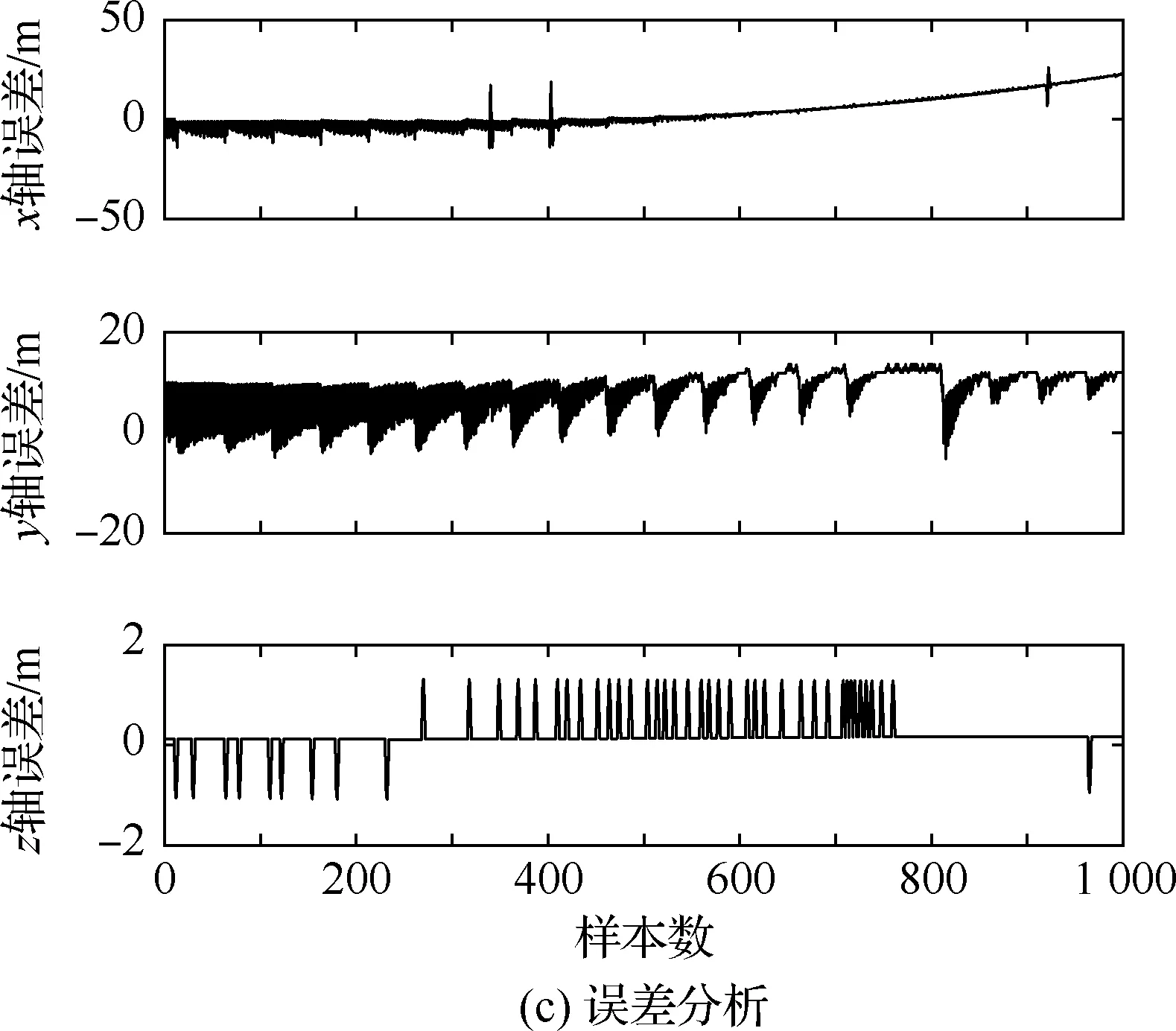
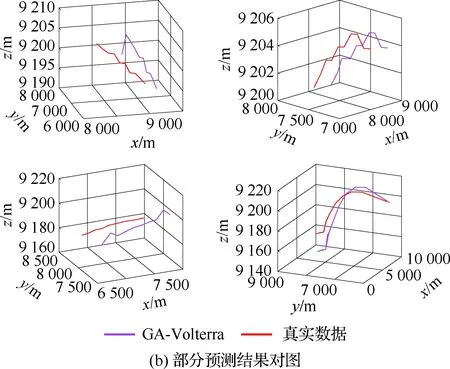
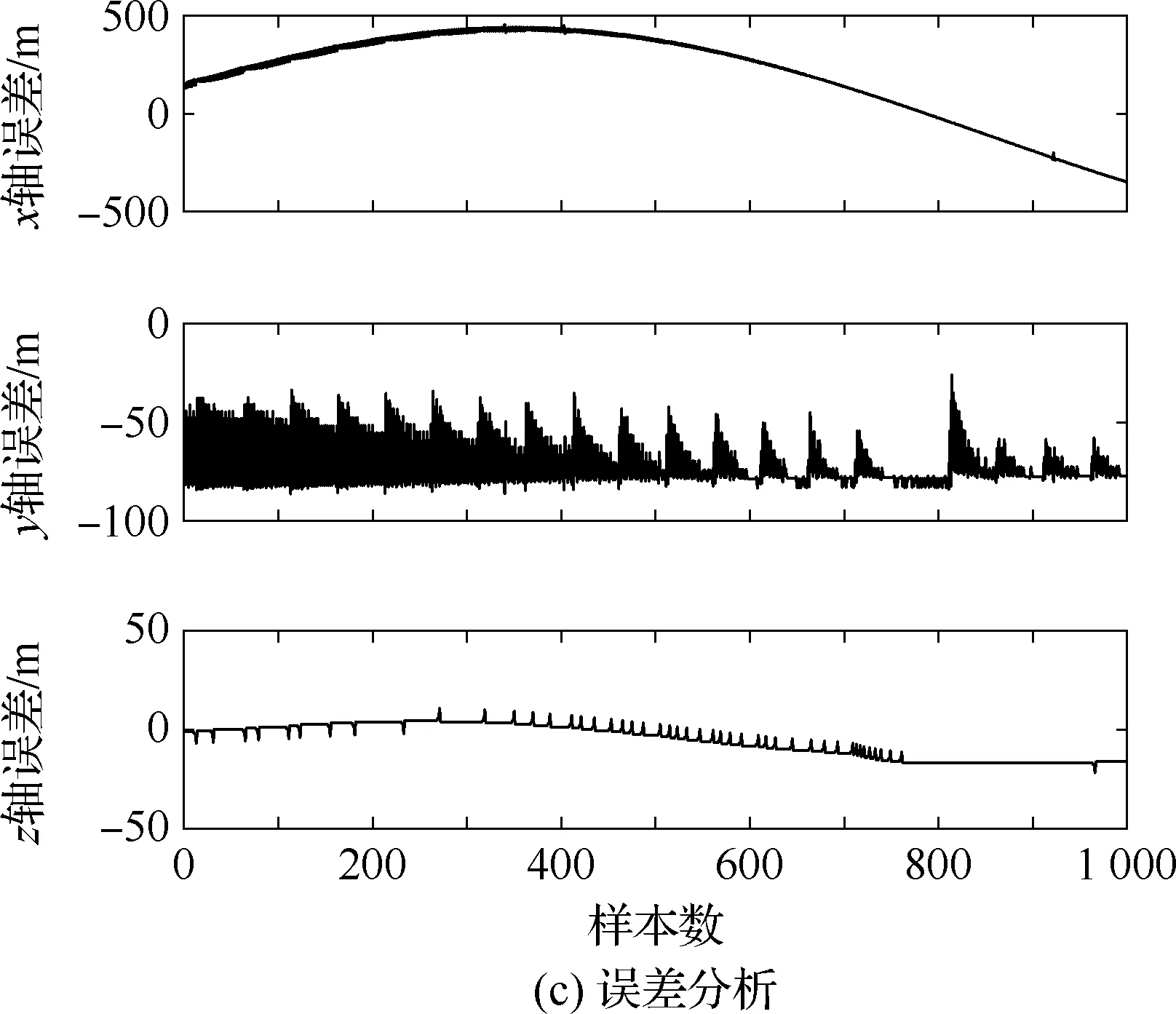
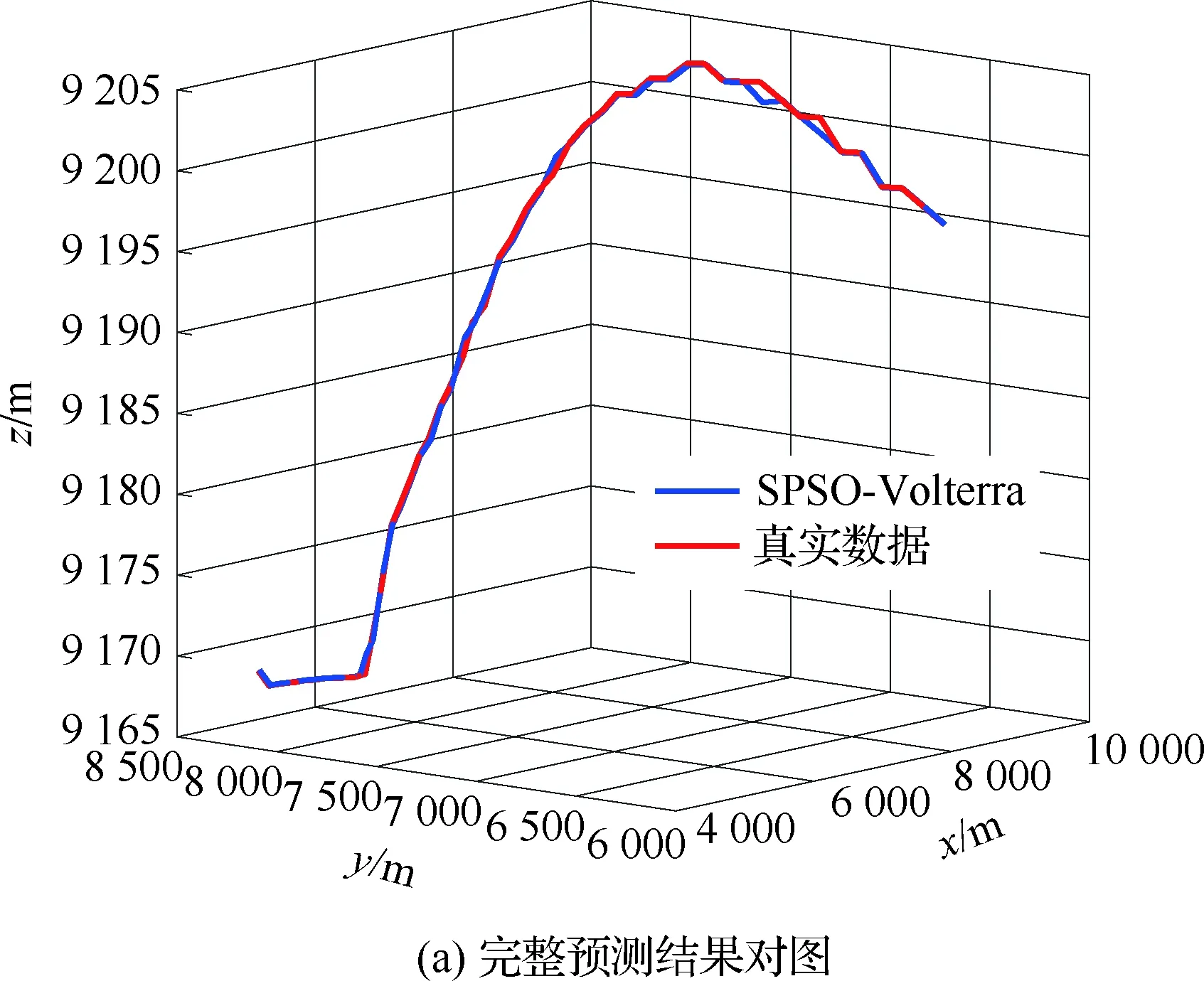
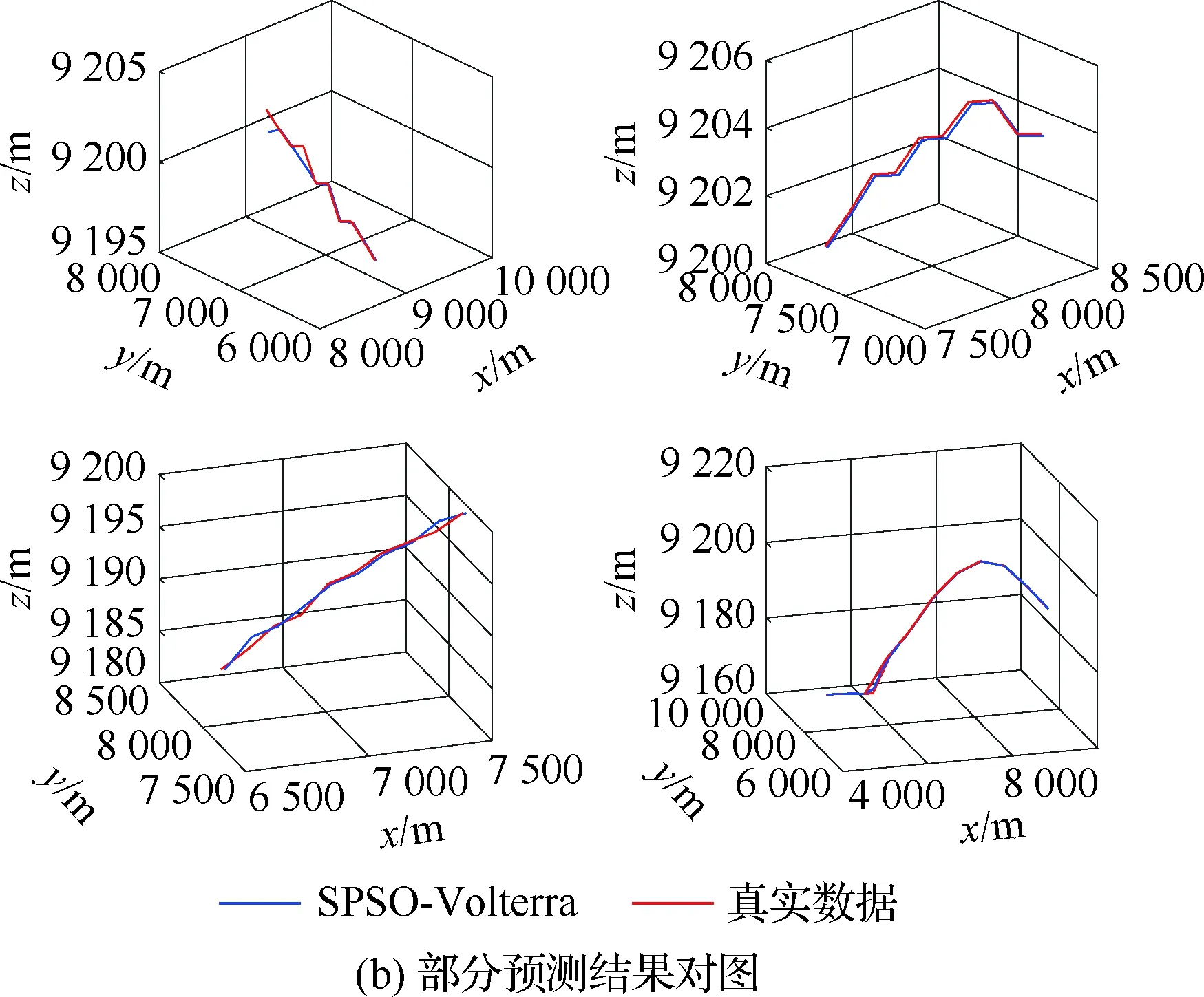
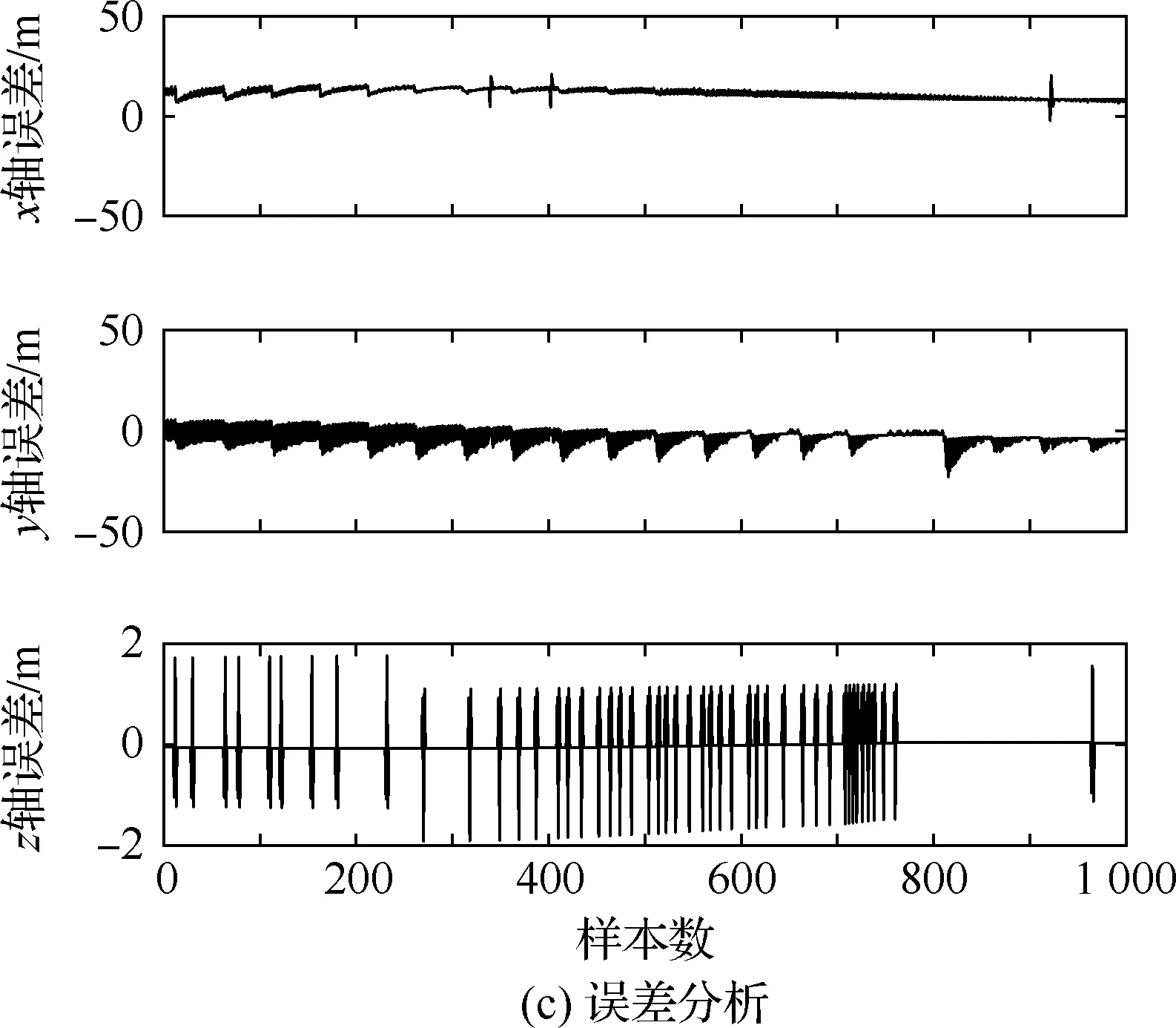
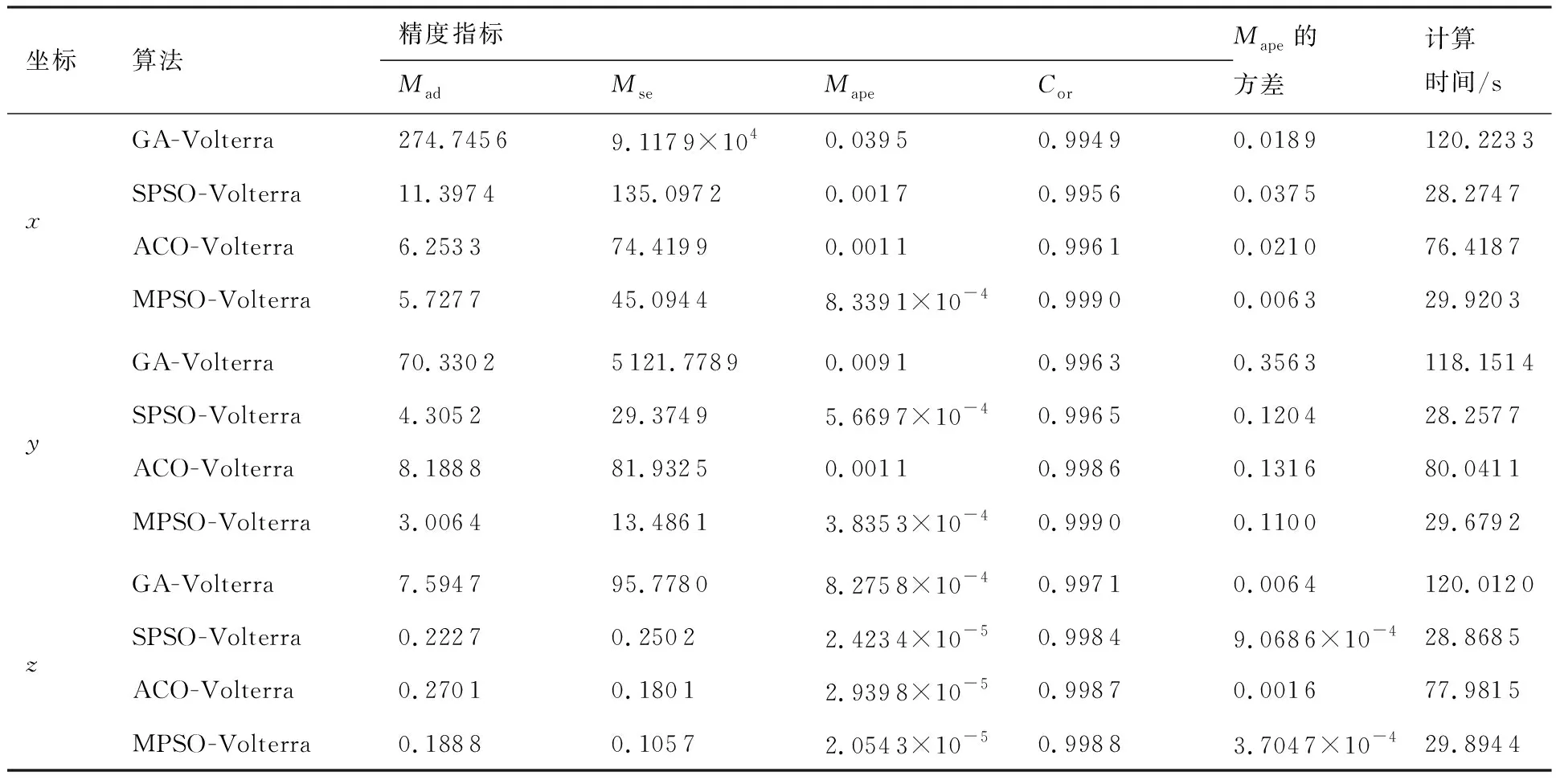
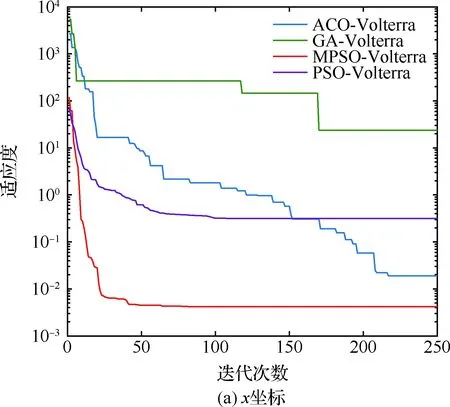
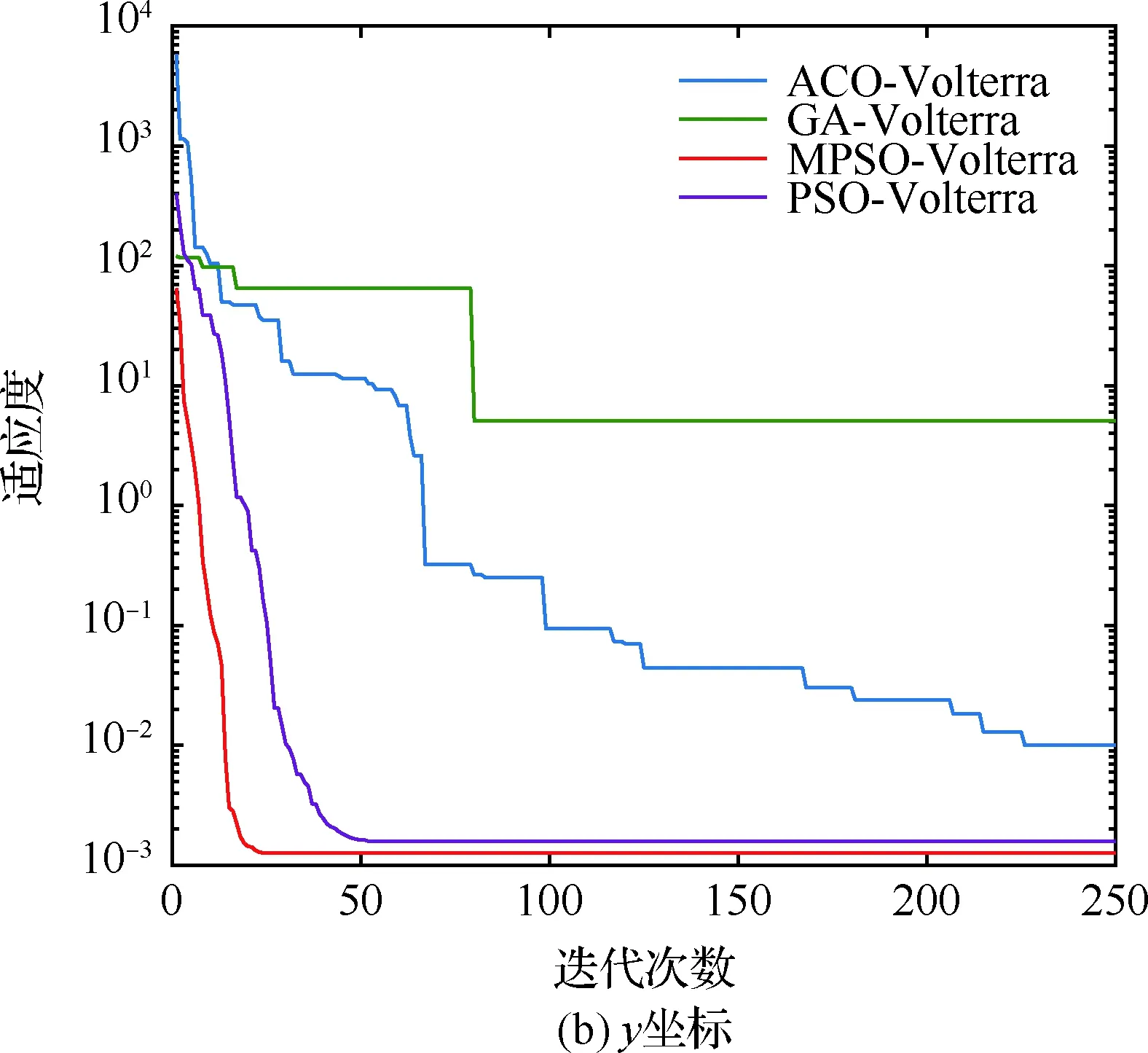
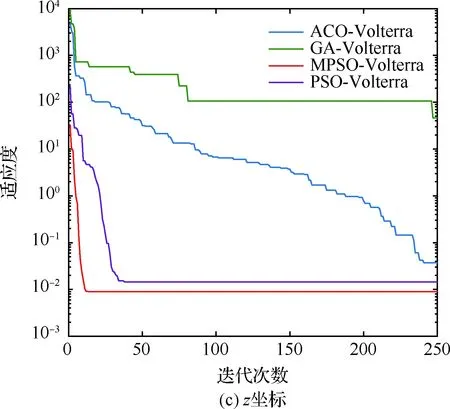
算法1:基于Skew-Tent映射初始化粒子种群设置粒子种群规模为n以及最大混沌迭代步数Kmax1.for i=1 to n do2.for j=1 to D do3.随机生成一个随机数φ0,j∈(0,1)4.for k=1 to Kmaxdo5.if 0 3.1.2 子种群划分 假设X(t)={X1(t),X2(t),…,Xn(t)}为算法第t次迭代时的粒子群,f(Xj(t))为第j个粒子的适应度值,适应度函数值越小则表明粒子的位置越优,根据粒子的适应度值定义一些概念: (30) fbest(X(t))=min{f(Xj(t))|j=1, 2, …,n} (31) Xgood(t)={Xj(t)|f(Xj(t)) j=1, 2, …,q; 1 (32) (33) 式中:favg(X(t))为粒子群平均适应度;fbest(X(t))为粒子群最优适应度;Xgood(t)为粒子群的优秀子种群;favg(Xgood(t))为粒子群优秀子种群的平均适应度。基于式(30)~式(33)定义的新概念,可以构建粒子群的精英子种群和普通子种群 Xelite(t)={Xj(t)|f(Xj(t)) j=1, 2, …,s; 1 (34) Xcommon(t)={Xj(t)|f(Xj(t))>favg(Xgood(t)); j=1, 2, …,p;p=n-s} } (35) 式中:Xelite(t)为精英子种群;Xcommon(t)为普通子种群;s为精英子种群规模;p为普通子种群规模。 3.1.3 自适应惯性权重调整策略 1) 精英子种群自适应惯性权重调整策略 假设ωj(t)为第j个粒子在第t次迭代时的惯性权重。为了说明改进粒子群算法中精英粒子群的ωj(t)调整策略,定义: fworst(Xelite(t))=max{f(Xj(t))| j=1, 2, …,s} (36) Perforj= (37) 式中:fworst(Xelite(t))为精英粒子群最差适应度;Perforj为精英粒子种群的性能指标,其取值范围为[0,1],精英粒子的适应度越好则性能指标Perforj越大,反之则越小;参数α的取值依据具体问题来确定。 将精英粒子种群性能指标Perforj作为第j个精英粒子在第t次迭代时的惯性权重自适应调整因子,则根据性能指标Perforj确定的自适应惯性权重为 ωj(t)=ωmin+(ω′-ωmin)×(1-Perforj(t)) ωmin<ω′<ωmax (38) 式(38)说明,性能指标Perforj越大的精英粒子,在其附近搜索到全局最优解的概率越大,然而较小的惯性权重可以增强算法的局部搜索能力,因此此时的惯性权重ωj(t)应该取较小值,从而保证算法的局部搜索能力;反之,性能指标Perforj越小,在其附近搜索到全局最优解的概率越小,较大的惯性权重可以增强算法的全局搜索能力,因此此时的惯性权重ωj(t)的取值应该较大,从而保证算法的全局搜索能力。 2) 普通子种群自适应惯性权重调整策略 在改进的粒子群算法中,普通子种群调整为 (39) 式中:t为算法的迭代次数;Tmax为最大的迭代次数。 3.1.4 混沌变异策略 1) 算法的收敛测度 为了更好地反映粒子群所处的状态,避免因为盲目变异而带来的大量运算以及对算法收敛速度的影响,本文提出利用粒子群的进化深度系数来定量描述粒子群状态,从而达到合理进行变异操作以扩大算法搜索空间的目的。 (40) (41) 2) 混沌变异策略 根据算法收敛测度判断算法是否陷入局部最优解,当算法陷入局部最优值时,采取混沌变异使得其跳出局部极值。混沌变异策略的步骤如下: 步骤1采用Skew-Tent混沌映射模型,基于式(26)生成混沌变量XT。 步骤2基于混沌变量生成粒子的混沌扰动量Xnew,即 (42) 3) 利用混沌变量对粒子进行混沌扰动: (43) 利用改进的粒子群算法对Volterra级数参数进行辨识,在此基础上,利用辨识之后的Volterra级数模型对目标机动轨迹进行预测,具体流程如图1所示。 图1 基于MPSO的Volterra模型辨识算法流程图Fig.1 Flow chart of identification algorithm of Volterra kernel based on MPSO 通过仿真检验本文算法的性能,同时与标准粒子群优化(SPSO)算法、遗传算法(GA)以及蚁群优化(ACO)算法进行对比。考虑三阶Volterra模型: y(k)=1.56x(k)-x(k-1)+0.68x(k-2)+ 0.85x2(k)-2.17x2(k-1)+ 1.39x2(k-2)+1.18x(k-1)x(k-2)+ 1.26x3(k)-0.83x(k)x2(k-1)+ 1.69x(k-1)x2(k-2)+1.41x3(k-2) (44) 式(44)Volterra级数模型中的一~三阶核的记忆长度均为3,核系数向量为 H=[1.56, -1.00, 0.68, 0.85, 0, 0, -2.17, 1.39, 1.26, 0, 0, -0.83, 1.69, 0.00, 0, 0, 0, 1.41]T 本文中所使用的仿真软件为MATLAB 2017a,仿真环境:CPU为Intel Core i7 2.60 GHz,内存为16 GB,操作系统为Microsoft Windows 10。本文所采用算法的初始参数设置如表1所示。为了保证算法性能比较的客观性,所有仿生智能算法均采用:种群规模N=50;空间维数D为19,即为Volterra级数核系数个数;最大迭代次数Tmax=250。表2为4种算法对Volterra级数模型进行辨识的结果,Rou为信息表的挥发因子。 表1 智能算法参数设置Table 1 Parameter setting of intelligent algorithm 表2 Volterra级数模型辨识结果Table 2 Estimation results of Volterra model 通过表2可以看出,4种辨识Volterra级数模型的算法均可以得到近似于真实值的核系数,说明这4种算法均能够用于Volterra级数模型的参数辨识,其中本文改进的粒子群算法得到的估计值与真实值更加接近,辨识精度更高。 本文主要对比MPSO-Volterra模型与其他预测模型在预测精度、算法实时性和稳定性方面的性能差异。预测精度采用平均绝对误差(Mean Absolute Deviation,Mad)、均方误差(Mean Square Error,Mse)、平均绝对百分比误差(Mean Absolute Percentage,Mape)和相关系数(Correlation Coefficient,Cor)4个指标来衡量,性能指标定义为 (45) (46) (47) (48) 对于不同的预测算法的运行效率,可以采用在相同的仿真环境下,计算相同的问题所需要的时间来评价;对于模型的稳定性,可以采用在相同的仿真环境下重复性实验结果的方差来评定。 在三维惯性坐标系中,飞机坐标用三维坐标x、y、z进行表示。传统的目标机动轨迹预测方法时间目标的三维坐标作为一个整体来预测模型的输入和输出,而本文基于对相空间重构理论分析可知,目标的轨迹三维坐标时间序列所呈现出的数据特征不尽相同,故需要将其进行独立预测。 本文从空战训练测量仪(Air Combat Maneuvering Instrument,ACMI)中选取一段时间连续的4 000组数据,将其中前3 000组数据作为预测模型的训练数据,后1 000组数据作为预测模型的测试数据。为了提高目标机动轨迹三维坐标的预测精度,首先基于相空间重构理论对目标机动轨迹时间序列进行相空间重构。根据C-C法确定目标机动轨迹x方向嵌入维数mx=7和时间延迟τx=9;y方向的时间延迟τy=5,嵌入维数my=8;z方向的嵌入维数mz=8,嵌入维数τz=2。采用单步预测方式,设置预测步数η=1。模型输入为[T(k),T(k-τ),…,T(k-(m-1)τ) ],且T=X,Y,Z预测模型输出为T(k+1) 。 4.3.1 目标机动轨迹单步预测效果对比分析 鉴于目前关于目标机动轨迹研究存在两类方法,即基于卡尔曼滤波算法以及以神经网络为主的机器学习智能算法,为了对比分析本文所提出的MPSO-Volterra级数预测模型与上述两种算法的优劣,分别采用本文预测算法与BP神经网络、ELM神经网络以及Kalman滤波算法对目标机动轨迹进行预测,通过性能指标来分析基于不同预测机理的预测算法之间存在的差异。 采用4种机理的不同预测算法对目标机动轨迹的三维坐标进行预测,预测结果如图2~图5所示,同时为了更加清晰地反映不同机理预测方法的性能差异,故将不同的算法的性能指标记录在表3中。由于本文采取的是中远距对抗数据样本,导致数据量级较大,同时本文预测算法误差较小,与真实数据之间的量级差异导致在预测结果对比图中,不能清晰看出预测值与真实值之间的差异,故各选取了4段区域预测情况进行局部预测效果呈现。 图2 MPSO-Volterra模型预测结果对比Fig.2 Comparison of prediction results of MPSO-Volterra model 首先,通过观察图2~图5中基于不同机理的预测算法对目标机动轨迹三维坐标进行预测的结果,可以看出,无论是基于卡尔曼滤波算法,还是基于神经网络,抑或是基于仿生智能算法辨识的Volterra级数预测算法,在对目标机动轨迹三维坐标进行预测时,其误差都是比较小的,这就说明基于3种机理的预测算法适用于目标机动轨迹预测问题。其次,通过表3中预测性能指标可以看出,基于仿生算法辨识的Volterra级数预测模型的性能更佳,而基于卡尔曼滤波算法和ELM神经网络的预测算法的性能较MPSO-Volterra级数预测模型差一点,说明MPSO-Volterra级数预测模型在目标机动轨迹预测方面更具有优势。 图3 Kalman滤波模型预测结果对比Fig.3 Comparison of prediction results of Kalman fillter model 图4 ELM神经网络模型预测结果对比Fig.4 Comparison of prediction results of ELM neural network model 图5 BP神经网络模型预测结果对比Fig.5 Comparison of prediction results of BP neural network model 从机理上分析可知,MPSO-Volterra级数预测模型本质上是利用目标机动轨迹时间序列的混沌特性,通过拟合训练混沌吸引子轨道来预测非线性系统,通过线性三阶Volterra级数的乘积耦合方式来实现,因此可同时避免因级数阶数较大而导致核函数求解困难和大量存在非线性耦合对Volterra级数核系数不收敛或不稳定的影响,提高了预测精度。另一方面,Volterra级数利用线性自适应算法调整模型参数,这种动态性可以提高其利用新数据预测的适应性和准确性。但是也存在一定的不足,采取仿生算法辨识Volterra级数预测模型计算时间较长,这是因为,算法的复杂度高于其他预测算法,自然预测模型的运行时间多余其他预测算法,根据NFL(No Free Lunch)理论可知,任何一个算法不可能全面优于其他算法,但是存在的这一点不足也是后续着重研究的算法,尽可能提高算法的实时性。 4.3.2 目标机动轨迹多步预测结果对比分析 表4 4种目标x方向坐标多步预测模型性能比较Table 4 Performance comparison of target x-coordinate multi-step prediction of four different prediction methods 表5 4种目标y方向坐标多步预测模型性能比较Table 5 Performance comparison of target y-coordinate multi-step prediction of four different prediction methods 表6 4种目标z方向坐标多步预测模型性能比较Table 6 Performance comparison of target z-coordinate multi-step prediction of four different prediction methods 通过表4~表6中在不同预测步数下各个预测算法的性能指标数值可以看出,本文提出的MPSO-Volterra级数预测模型的性能更佳,Kalman滤波算法、ELM神经网络以及BP神经网络的预测性能在不同方向坐标预测中表现出不同的性能差异较大,这些都说明本文所提出的MPSO-Volterra级数预测模型更加适用于目标轨迹预测问题。从机理上分析各种算法表现出不同的预测性能的原因: 1) BP神经网络是一种单隐含层前馈神经网络,其可以通过样本数据不断地训练学习拟合任何输入、输出之间的各种复杂的非线性关系,具有一定的鲁棒性和泛化能力,但是BP神经网络算法自身也存在一定的“缺陷”,由于BP神经网络算法在学习的过程中采用标准梯度下降算法,在采用样本对其进行训练时,易陷入局部极值,导致样本学习失败;同时,BP神经网络算法也存在学习“过拟合”的现象,一般情况下,BP神经网络的预测能力与样本训练能力呈正相关,但是实际上随着样本训练能力的提高,BP神经网络预测能力会达到一个极限值,随后会出现预测能力下降的现象,故BP神经网络在预测过程中存在一些自身无法克服的不足,因而预测性能也会有所影响。 2) ELM神经网络与传统的神经网络算法相比,ELM神经网络具有相对明显的优势,但同时也存在一定的固有缺陷:一方面,网络的输入层与隐含层之间的权值、阈值进行随机确定,因而具有一定的盲目性,从而导致ELM网络的稳定性变差;另一方面,如果训练数据中存在噪声或离群点,容易导致网络的隐含层输出矩阵呈现出病态的问题,使ELM神经网络的鲁棒性变差、泛化性能降低。在复杂的电磁环境下,基于机载传感器获取的目标机动轨迹,很容易出现一些离群点,从而导致ELM神经网络预测性能下降。 3) Kalman滤波算法采用不断“预测-修正”的递推方式进行,先进行预测,再根据观测值得到的新息和卡尔曼增益对预测值进行修正。卡尔曼滤波通过迭代来消除估计误差,但误差具有传递性,随着迭代次数的增加,目标运动状态估计的精度也会随之下降。同时,新息反映了预测值偏离观测值的程度,当目标的运动状态发生突变或者目标运动模型不够准确时,目标下一时刻的运动状态预测精度降低,空战中目标的运动模式是不断变化的,很容易导致算法预测精度下降;由于卡尔曼滤波预测算法需要实时更新新息来修正预测误差,在进行多步预测时,目标的实时新息得不到更新,算法的预测精度也会随之下降,在空战中目标的信息获取并不是可以实时准确获得的,因Kalman滤波算法在空战中进行多步预测存在不足。 4) Volterra自适应滤波器预测模型在预测过程中仅需很少的数据样本就可对混沌时间序列进行预测,而且可自动追踪混沌运动轨迹,该预测模型的预测精度较高。 4.4.1 机动轨迹时间序列预测效果对比 本节将本文提出的基于改进粒子群优化的Volterra级数预测模型与GA算法优化的Volterra级数预测模型、ACO算法优化的Volterra级数预测模型以及SPSO算法优化的Volterra级数预测模型对目标机动轨迹时间序列单步预测结果进行对比,预测结果对比如图2、图6~图8所示。 图2、图6~图8代表了4种智能算法辨识的Volterra级数预测模型对目标机动轨迹预测的结果对比曲线和误差曲线。从图中可以看出,在采用4种智能算法辨识的Volterra级数预测模型对目标机动轨迹的三维坐标进行预测时,各个点的误差均在零点附近较小范围内波动,说明4种智能算法对Volterra级数辨识的有效性,说明群智能优化算法能够有效解决Volterra级数核函数求解困难的问题,同时也说明了Volterra级数具有优良的非线性拟合和预测能力;同时也存在一些将来需要解决的问题,如何选择优化算法以及怎样改进优化算法的问题,本文仅仅初步探索,利用群智能优化算法辨识Volterra级数,并将辨识之后的Volterra级数模型用于预测问题。 图6 ACO-Volterra模型预测结果对比Fig.6 Comparison of prediction results of ACO-Volterra model 图7 GA-Volterra模型预测结果对比Fig.7 Comparison of prediction results of GA-Volterra model 图8 SPSO-Volterra模型预测结果对比Fig.8 Comparison of prediction results of SPSO-Volterra model 为了对比分析不同优化算法辨识的Volterra级数预测模型在预测精度、速度和稳定性上的不同,在相同的仿真条件下,分别采用SPSO-Volterra、GA-Volterra和ACO-Volterra模型对目标机动轨迹时间序列进行单步预测。每一种预测模型独立重复运行50次,统计得到模型预测结果的平均绝对误差、均方误差、平均绝对百分比误差、线性相关度以及算法的平均运行时间。其中,平均绝对百分比误差是反映预测值和真实值之间偏离程度的重要指标,预测模型的稳定性采用Mape的方差来评价。表7给出了不同的预测模型对目标机动轨迹时间序列进行预测时所呈现的性能。 从表7可以看出,与其他优化算法辨识之后的Volterra级数预测模型相比较,在预测精度方面,MPSO-Volterra预测模型的Mad,Mse以及Mape的值均是最小,Cor最高,这些可以说明MPSO-Volterra预测模型在目标机动轨迹时间序列的预测精度上具有明显的优势。在预测稳定性方面,MPSO-Volterra预测模型的平均绝对百分比误差Mape的方差最小,这说明MPSO-Volterra预测模型的稳定性最好。在算法的运行速度方面,MPSO-Volterra预测模型和SPSO-Volterra预测模型所需要的计算时间远少于ACO-Volterra预测模型和GA-Volterra预测模型,由于MPSO-Volterra预测模型中执行了自适应参数调整机制和混沌变异机制,导致其运行时间略多于SPSO-Volterra预测模型。综合来看,在目标机动轨迹时间序列预测中,MPSO-Volterra预测模型相较于其他预测模型,在预测精度、速度以及稳定性方面均具有模型优势。 4.4.2 不同算法优化性能对比 对目标机动轨迹的三维坐标分别进行建模与预测时,PSO-Volterra算法、GA-Volterra算法和ACO-Volterra算法以及本文所提MSPO-Volterra算法的收敛曲线对比结果见图9。横坐标为算法迭代次数,纵坐标为算法的适应度函数的适应值。 在图9(a)中,x坐标下ACO-Volterra、GA-Volterra、PSO-Volterra和MSPO-Volterra算法的适应度函数值达到稳定时的迭代次数分别是217、170、81、139;在图9(b)中,y坐标下4种算法的适应度函数值达到稳定时的迭代次数分别是241、81、15、91;在图9(c)中,z坐标下4种算法的适应度函数值达到稳定时的迭代次数分别是226、80、22,48。因为是将Volterra级数的预测误差设定为智能优化算法的适应度函数,适应度函数值越大,则Volterra级数预测误差越大,通过上述分析可见,对比与现有的智能算法辨识Volterra级数模型,本文所提出的MPSO-Volterra级数算法模型不仅具有较高的收敛精度,同时还具有较快的收敛速度。 表7 各种算法对目标三维坐标的预测性能指标Table 7 Prediction performance indexes of various algorithms for target 3D coordinates 图9 适应度函数值比较Fig.9 Comparison of fitness function values 从机理上分析可知,粒子群算法是一种基于种群模拟的群体仿生智能优化算法,具有运行时间短、容易收敛以及鲁棒性强的优点,然而非线性系统Volterra级数核函数辨识实际上是一个高维度优化问题,PSO算法在面对优化高维度问题时,容易出现早熟现象,导致算法陷入局部最优而无法跳出,同时还存在收敛精度不高的问题。GA算法在用于参数辨识时,存在一些自身无法克服的问题,即优化时间长且容易陷入局部最优。由于ACO算法中的多个个体的运动是随机的,随着蚁群种群的增大,寻找到一条较优的路径需要更多的时间,此外,ACO算法中融入了正反馈机制,如果正反馈过于强,容易使得算法陷入局部最优,反馈过弱,则使得算法收敛速度减慢。针对上述机理分析,GA、PSO以及ACO算法在参数辨识问题或者高维度优化问题上都存在一定的不足,本文所采取自适应策略和混沌变异策略可以有效提高基本粒子群算法在高维度问题优化方面所呈现出的不足。 本文对目标机动轨迹时间序列进行了相空间重构,同时对其进行了混沌特性的判定识别。引入基于改进粒子群算法辨识的Volterra泛函级数模型,建立一种基于Volterra级数的目标机动轨迹预测模型。 1) 本文采用0-1检测法对目标机动轨迹时间序列进行了混沌判定。结果表明:实际记录的目标机动轨迹存在混沌现象,实际记录的目标机动轨迹时间序列为混沌时间序列。0-1检测法可以较准确地判断时间序列中是否含有混沌特性,从而为时间序列的分析与预测提供前提。 2) 由于已确定目标机动轨迹存在混沌现象,本文引入非线性Volterra模型,结合智能优化算法,建立了基于改进粒子群算法辨识的Volterra自适应预测模型。该预测模型综合利用线性和非线性因素,充分利用了目标机动轨迹的混沌特性,更符合混沌序列的非线性本质。实验结果表明,三阶Volterra自适应预测模型能够很好地对目标机动轨迹做出预测,且预测精度较高。 3) 本文将改进的粒子群算法与非线性Volterra泛函级数模型相结合,同时在仿真中,将该预测方法与Kalman滤波算法以及机器学习算法的预测性能进行了对比分析。实验结果表明,本文提出的算法在单步和多步预测方面的性能都较好,可以适用于目标机动轨迹预测问题。 4) 本文将改进的粒子群算法与非线性Volterra泛函级数模型相结合,同时在仿真中,将该预测算法与SPSO-Volterra模型、ACO-Volterra模型和GA-Volterra模型的预测性能进行了对比分析。实验结果表明,本文提出的算法预测精度高,且算法的收敛速度快。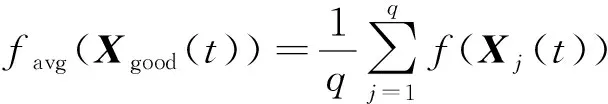
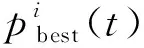
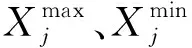
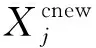
3.2 Volterra级数目标机动轨迹预测流程
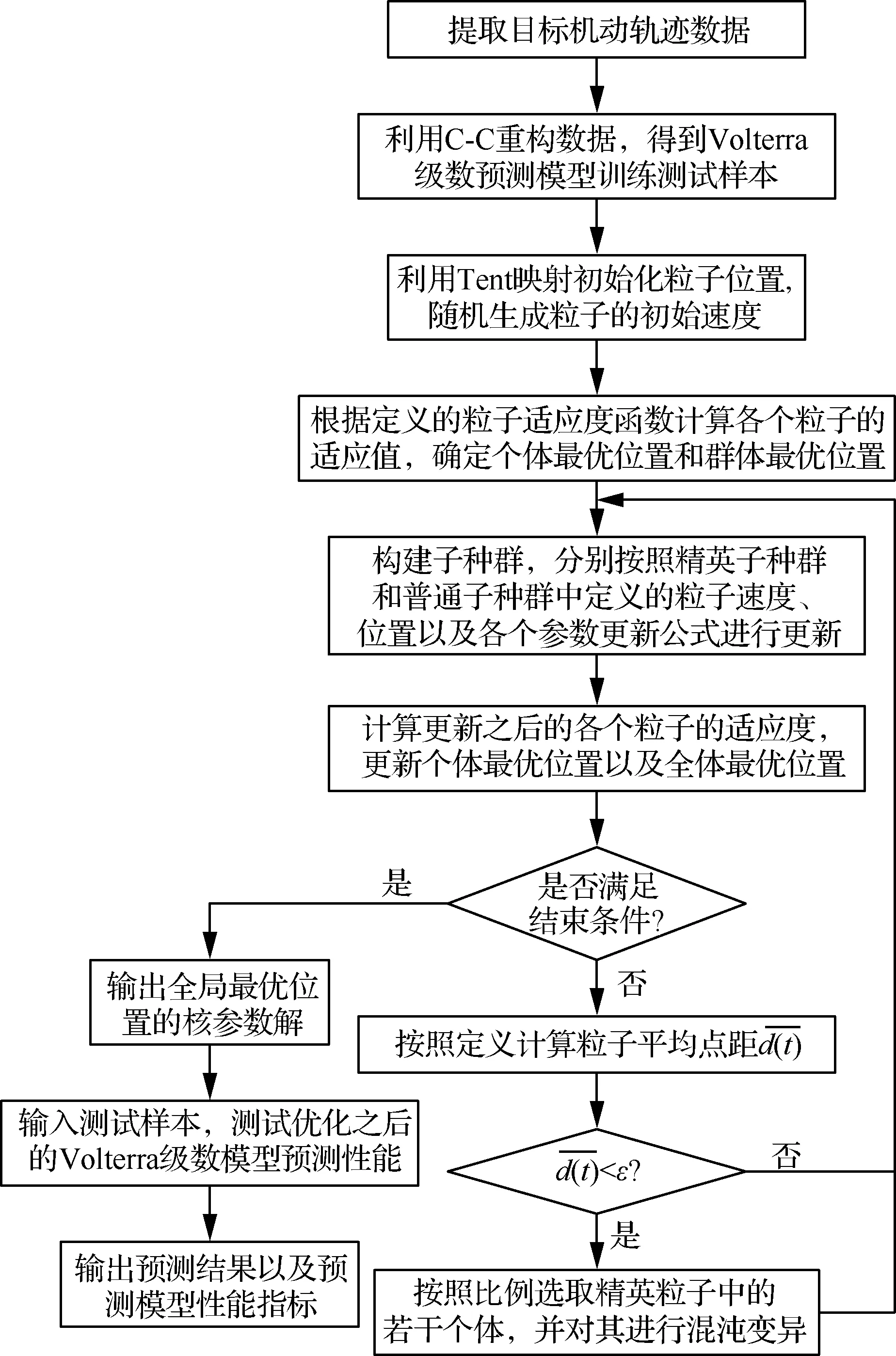
4 仿真验证
4.1 Volterra级数模型辨识测试

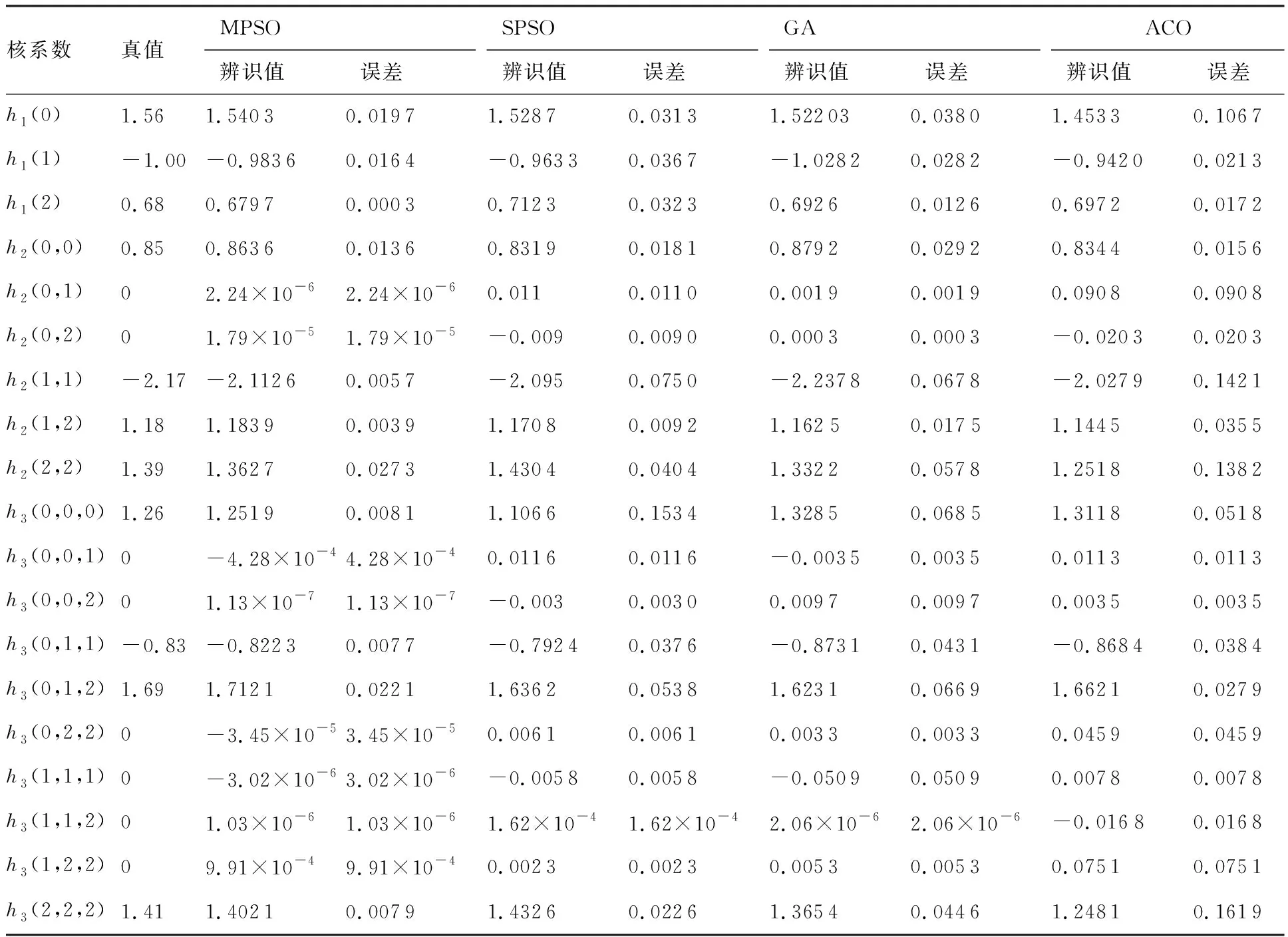
4.2 预测算法性能评价

4.3 不同模型单步及多步预测性能对比与分析
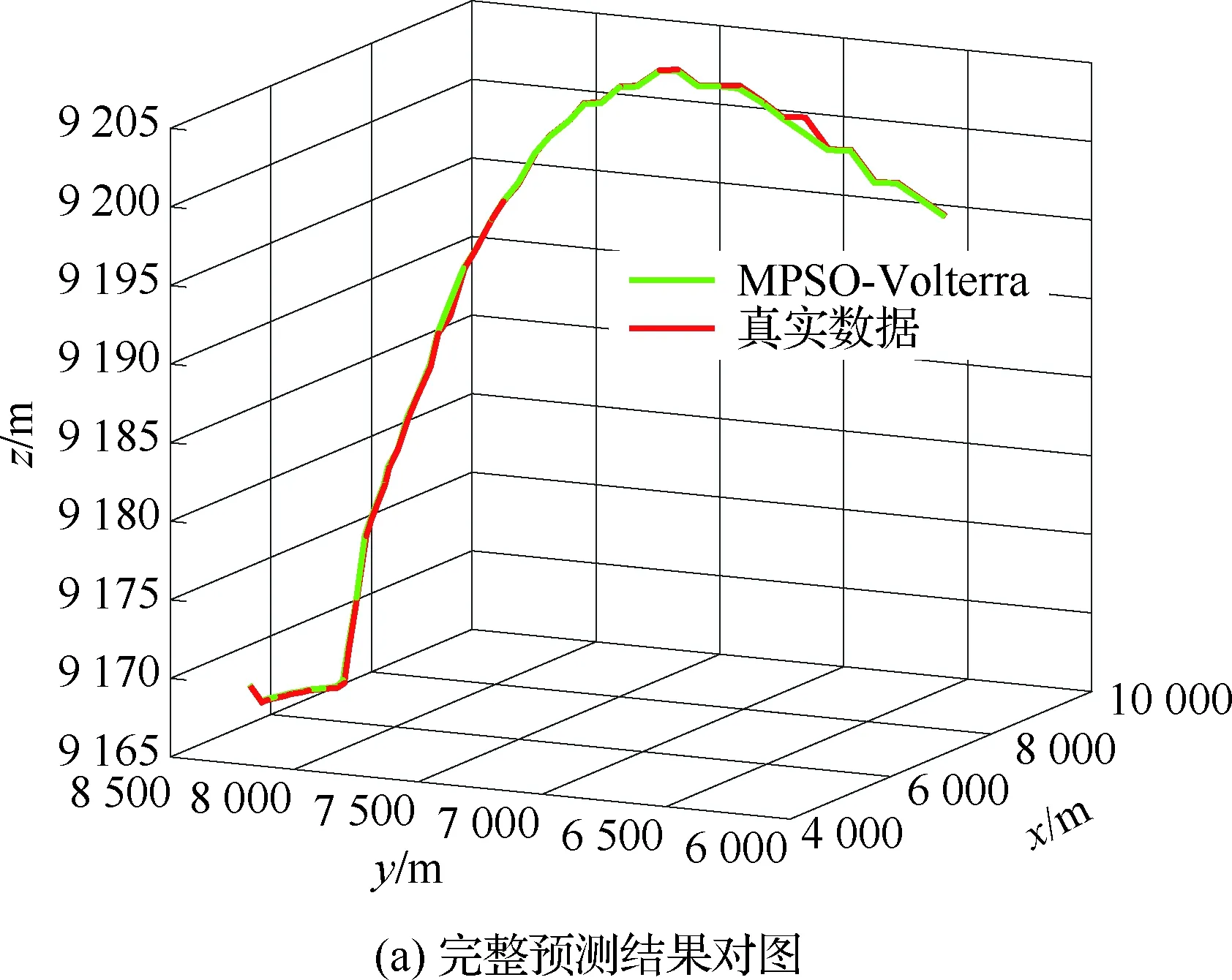
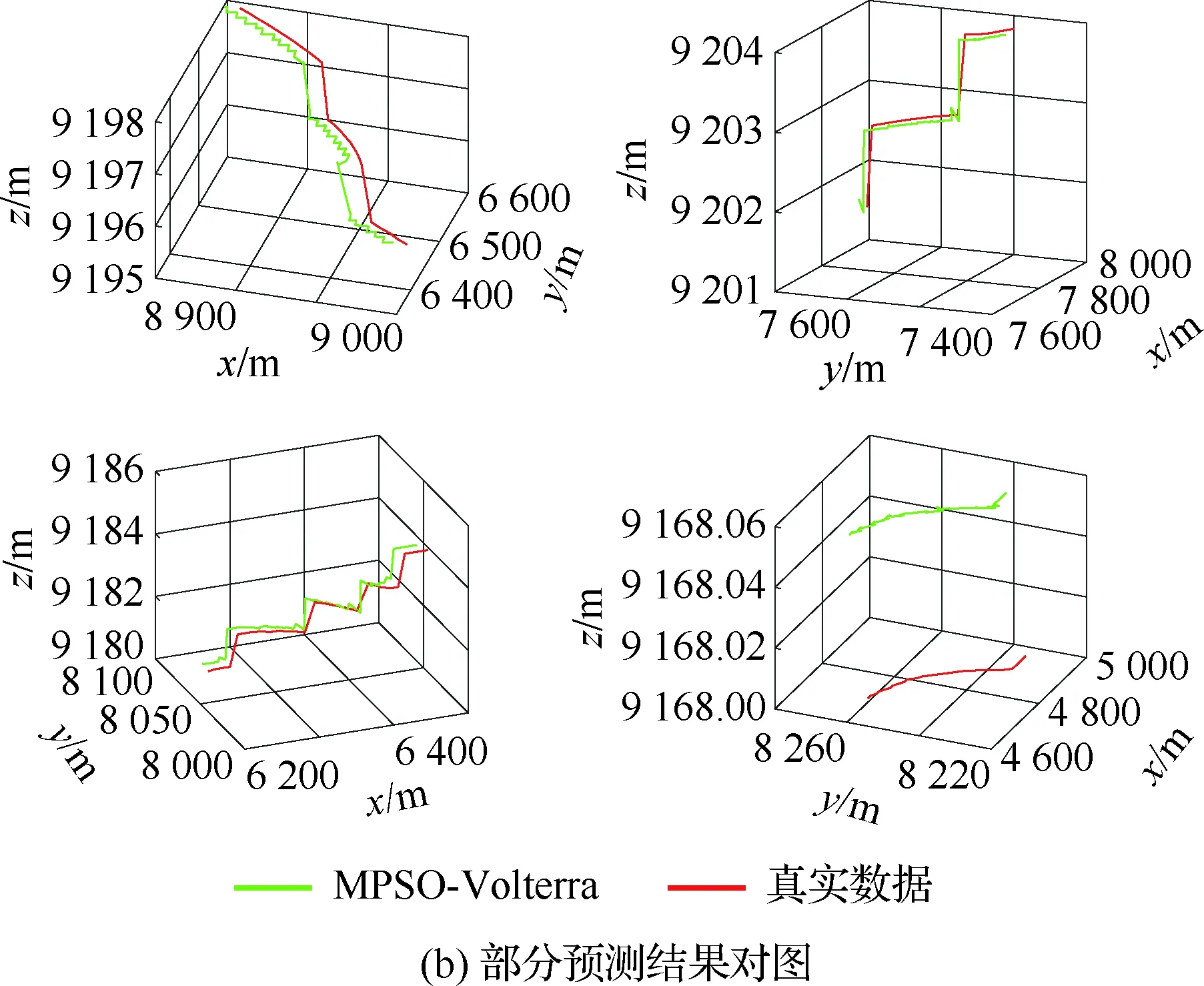


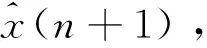
4.4 不同优化算法性能对比
5 结 论
