基于SEIR模型的疫情预测模型及应对措施

2020-12-28黎涵予邵振东王恒博都鸿宇

中国电气工程学报 2020年19期

黎涵予邵振东王恒博都鸿宇

【摘要】2019年底爆发新冠肺炎疫情，在各國大面积蔓延。本文建立了SEIR模型，给予模型中的各符号一个假定且符合实际情况的数字。通过对微分方程的求解得出，易感者、感染者、潜伏者、康复者之间的关系，对潜伏者的数量进行预测，将模拟结果和实际情况进行对比分析，说明我们模型的可行性。并结合当前情况进行预测，在原假定数字的基础上进行合理修改，将修改后的模型与原模型进行对比，得出疫情防控的作用，并给出合理的建议和减少风险的措施。

【关键词】新型冠状病毒;SEIR模型;微分方程

2020 年 3 月 12 日，世界卫生组织（WHO）宣布，席卷全球的冠状病毒引发的病毒性肺炎（COVID-19）是一种大流行病[1]。截至2020年9月20日，全球已有超过30000000例累计确诊，超过95000例累计死亡病例。由此对疫情发展预测，以及提出对应措施，对疫情防控具有重要意义。

一、数据来源

此文中我们将问题简化，使用抽样模型，采用分区分块抽样的方式，在大规模城市中，按城市规划划区，再在区域内划块，在抽样中分为三个阶段，各阶段中采用分层抽样、概率比例规模抽样与等距系统抽样，降低在大规模城市中抽样难度，在较短的时间内得到更高质量的样本[2]。具体数据在下方表中赋值。

二、SEIR模型的介绍与构建

1.模型介绍

SIER模型用于研究传染病的传播速度、空间范围、传播途径、动力学机理等问题，以指导对传染病的有效地预防和控制[3]。其结构如下：

2.模型的建立

为适应实际情况，假设某一地区T时刻总人口数为N，地区人口数量稳定，没有人口的迁入迁出。S表示未染病但是有可能被疾病传染的人数占总人口的比例，I表示已被疾病感染成病人且具有传染性的人数占总人口的比例[4]。病人在被感染后有一段时间的潜伏期，假定在潜伏期内的感染者具有传染性，记T时刻潜伏者人数占总人口数的比例为E，并假定病人康复后具有永久免疫力，可得到以下模型：

□（24&ds）/dt=-rβIS/N-r_2 β_2 E S/N（1）

dE/dt=rβIS+r_2 β_2 E S/N-αE（2）

dI/dt=αE-γI（3）

dR/dt=γI（4）

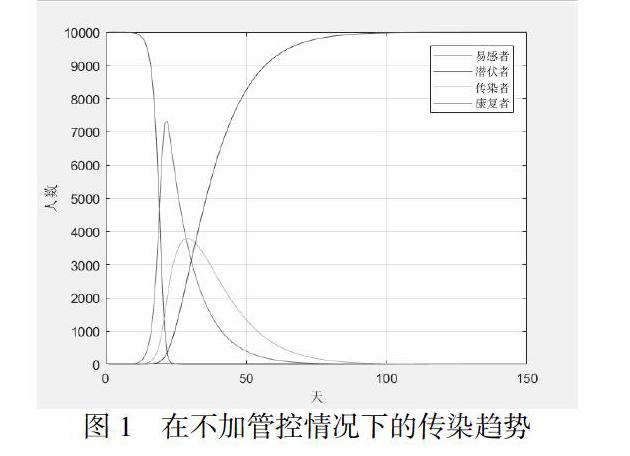
传播预测：

针对SEIR模型，若时间足够长，且不加以管控的话，所有人都会被感染，并且感染时有明显的爆发期如下图1所示

若政府对病毒的传播加以管控，将感染者进行隔离治疗，且每人都减少外出并戴好口罩做好防护，意味着减小了接触率和感染率，可以看到病毒的传播得到了极大的抑制和减缓，如图2 所示

3.模型的完善

本模型与实际情况有部分出入，若要完善此模型，可考虑上某地区的迁入迁出率，同时随着疫情的发展，无症状感染者也被发现，这意味着在未作检测的情况下，部分表面健康者可能携带病毒，可将此因素考虑到模型中，进而将模型完善。

三、疫情防控的建议

根据上面模型生成的结果，我们不难看出国家调控在疫情防控中的重要性，因为我们给出几点建议：

政府方面，随着九月份的推进，复工复产已经开始进行，疫情严重的国家必须根据情况进行工作，即使是疫情抑制住的国家也得谨慎复工，不然很有可能在流感高发的换季时期造成疫情的二次高峰。因为大部分的基层劳动者为非本地户籍人员，人员流动性较强，提高了迁入迁出率和传染概率。