模式识别在数学概念教学中的运用

招欣

【摘要】根据模式识别理论，数学概念是一种数学模式.在数学概念教学中，若教师发挥模式识别在情境创设、概念获得、概念巩固中的作用，则不仅有助于学生获得数学概念，而且有助于学生理解数学本质意义.

【关键词】数学教学;概念;识别

数学概念是反映事物本质属性的思维形式，是一类事物的内在、固有的屬性，而不是个别、表面的属性.作为一类事物的特征，数学概念也是一种数学模式.根据模式识别理论，数学概念的教学一般要经历从大量对象中识别特征，从众多特征中寻找联系与区别，区分本质特征和非本质特征，归纳、概括本质特征，解构本质特征，建构本质特征，变换本质特征或非本质特征的过程，可以使学生巩固头脑中的相关数学概念.

一、模式识别方法在情境创设中的运用

（一）创设跨学科单元的情境，丰富模式的意义

在教学中，教师可以根据概念特点设计跨学科单元的教学情境来引入数学概念.比如，教学向量的数量积概念时，教师可以从力的分解引入;教学正四面体的概念时，教师可以设计甲烷的化学结构情境.不同数学模式之间的联系促使数学知识形成一个有机整体.例如，在教学“倍”的概念时，教师可采用数形结合模式，将抽象的数学概念“倍”转化成形象的图形，使学生在体会与运用中深谙模式识别的意义.

（二）创设典型情境，为模式识别提供原型

数学概念是一种特殊的思维形式，反映了数学对象本质的属性.

创设典型情境的目的不在于引导学生识别某一个对象，而在于引导学生识别某一类客体共有的基本特征.例如，在教学二元一次方程的概念时，教师给出题目：在长为20 cm、宽为16 cm的长方形纸片的四角分别剪去大小相等的小正方形，做成一个无盖长方体盒子，设小正方形的边长为x cm，求（1）剪去的面积y与x的关系表达式;（2）盒子的表面积a与x的关系表达式;（3）盒子底面积s与x的关系表达式;（4）盒子较大的一个侧面积m与x的关系表达式.

“通过观察未知数的个数以及指数、表达式的项数，你有什么新发现？”，然后引导学生识别出一元二次方程的特征“形如y=ax2+bx+ca≠0，仅含一个未知数，且未知数的最高次数是2”.

学生识别出一元二次方程模式的本质特征后，便建立起一元二次方程的原型y=ax2+bx+c，而非y=x2.

（三）创设探究的数学情境，引导概念特征的识别过程

数学概念的抽象性导致学生对一些数学概念的理解存在一定困难，且教材对数学概念的形成与由来往往介绍较少，因此，学生在数学概念的学习中往往易产生畏惧甚至排斥的心理.考虑到学生的认识过程是由具体形象逐渐过渡到抽象这一特点，教师可以创设相关情境，启发学生从具体形象的实例中识别出概念的特征并归纳概括，引导学生进行模式识别的操作.在此过程中，教师应让学生根据自身经验和实践操作学习数学概念，而不是直接获得教师给予的纯粹的“数学概念”.

例如：在轴对称图形的教学中，教师先出示一组图片，如京剧脸谱、蝴蝶、昆虫标本、建筑物等，让学生观察这一组图片有什么共同特征，追问“你还能列举出具有这种特征的物体吗？”.学生在观察中很快会发现这些物体都是对称的.接着，教师以蝴蝶图片为例，通过多媒体演示蝴蝶图片沿中心线翻折的过程，以此让学生归纳概括出对称图形的共同本质特征.如果学生发现不了，那么教师可以从图形的形状、大小及位置关系方面提问，进一步启发学生思考.至此，学生对轴对称图形的本质特征进行了识别.

教学建议：数学概念产生的途径很多，有的数学概念源于生活实际问题，有的数学概念源于数学自身体系，更多数学概念源于这两者的结合.因此，在概念教学的情境创设过程中，教师需要以概念自身的产生背景为基础，围绕概念的本质创设情境，引导学生在数学情境中排除非本质、次要因素，识别归纳出概念的本质属性，初步建立概念表象，并在学生识别的过程中，启发学生找准识别角度，把握识别方向.

二、模式识别方法在概念获得中的运用

（一）多角度识别概念的本质特征

由于分析的角度不同，同一个数学概念表现出的含义也就不同.如在教学角的概念过程中，教师可以通过“组成角需要什么条件？”这一问题引导学生识别出角的特征.为了让学生全面、准确地把握角的概念的本质，教师可以用旋转的角度引导学生对角的概念进行进一步解构.教师将射线的旋转过程以动态的钟摆来呈现，射线旋转过程中扫过的面积即角的内部，也称角内;类推平面其余部分则为角的外部，也称角外.如此，教师就从静态和动态两个方面实现了对角的概念的解构.

（二）识别概念的外延

识别概念的外延即识别该概念所反映的全体对象.概念外延的识别可为进一步明确概念的本质奠定基础.

例如：在三角形的认识教学中，学生在生活中已经初步形成三角形的概念，若要使学生建立更加全面的三角形的概念，则识别三角形的外延就显得十分重要.在教学中，教师可以出示不同类别的三角形，启发学生思考：每个三角形的三个角分别是什么角？你能根据发现的特点把这些三角形分类吗？学生便由此建立角的概念.

（三）通过识别新旧概念间的联系与区别实现概念的获得

现代认知心理学认为，数学概念的获得过程是新概念与认知结构中原有相关概念内容相互作用后进一步完善认知结构的过程.因此，教师在概念获得的过程中引导学生识别新旧概念之间的联系与区别，并从中明确新概念的本质属性就显得格外关键.值得一提的是，这里为新概念做铺垫的旧概念知识必须是与新概念有关联的知识，如此才有识别的意义，即模式识别中的新旧概念之间关系的识别.

例如：在教学小学数学中“比”这一概念时，教师可以将学生已经掌握的“除法”概念与“比”概念进行比较，启发学生识别两个概念的同与异，从而建立“比”的概念.又如在教学“抽象的空间几何中的直线垂直”这一概念时，教师可以将“平面几何中直线垂直”的概念与其相比，引导学生在识别二者之间关系的基础上获得空间垂直的概念.

教学建议：在概念获得的过程中，学生在头脑中形成的数学概念是学生在识别特征的基础上归纳出来的，而不是教师强行灌输的，这一做法符合学生的认知发展规律.因此，在概念获得的教学过程中，教师可以引导学生從不同的角度识别概念属性，完成概念本质特征的识别，促进学生完成模式的建构.另外，教师可以以学生认知结构中的原有概念为新概念识别的起点，帮助学生在旧概念的基础上建构新概念，从而完成新概念的获得.

学生在此过程中需要学会用符号语言、图形语言、几何语言将数学概念表示出来，将数学符号赋予相应的数学概念.这也是学生符号意识发展的重要表现之一.

三、模式识别方法在概念巩固中的运用

（一）对模式进行变式

变式改变的是对象的角度、方法或非本质特征的表现形式，从而突出那些隐藏的、易被学生忽视的本质要素.概念建立后，教师可以根据学生识别过程中的难点、易混淆点设计相关练习.

练习1 圆的认识

分别指出图1中圆的直径和半径.在教学中，教师设置几个与半径、直径相似的线段让学生识别，进一步巩固学生关于直径、半径概念的内涵与外延.概念变式有标准变式和非标准变式两类.标准变式从某种程度上来说有利于学生准确把握概念，但同时会缩小概念的外延，使学生的思维变得狭隘.而非标准变式可以弥补这一缺陷，利用概念非本质要素的变更来突出其本质属性.

（二）对模式进行转换

在概念巩固的过程中，转换数学概念模式并将其与其他数学概念模式相联系，有助于学生在认知结构中已有的模式上拓展相关模式.

练习2 圆出于方

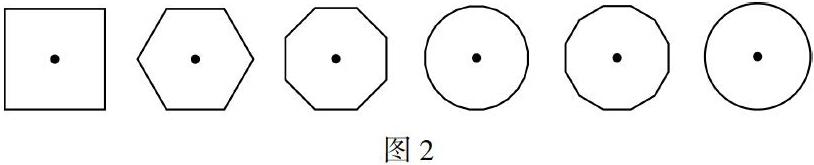
师：“圆出于方”的古语你们听过吗？如图2，我们可以通过如下的操作来近似得到圆.假设一个正方形的边长是 6 cm，那么在这个正方形里最大的圆的直径是多少？

生：圆的直径就是正方形的边长，就是6 cm.

师：如果不告诉你任何信息，你能找出一枚硬币的直径吗？

生：硬币四周紧贴正方形，硬币直径就是正方形的边长.

学生识别圆这一概念往往不能一次成功，其过程是螺旋上升式的.教师要引导学生进一步挖掘概念背后隐藏的数学本质，使学生头脑中不断修正、扩展并提升模式.

（三）对模式进行完善

一个阶段的学习完成之后，教师要引导学生将学习过的概念进行整理归纳，识别概念与概念之间的联系与区别，从而使促进学生掌握完整的概念模式.比如，学生在学了“比”的全部知识后，教师可以引导学生归纳整理“比”的概念，“比”与除法、分数的联系与区别，“比”的基本性质，以及根据“比”的基本性质化简“比”.这一系列模式的建立能很好地解决求比例尺和比例分配的关系.通过这一过程形成的相关概念的模式网络使学生在理解概念的基础上加深对数学本质的感悟.概念模式不断被完善，学生才能得心应手地应用概念解决实际问题.

教学建议：在巩固概念的过程中，为了加深学生对概念的认识，教师需要变换概念的非本质属性以对概念模式进行变式，进一步使学生在变化中识别概念中不变的本质.另外，在一个阶段的教学完成后，教师需要有意识地引导学生将学过的概念进行整理，并在新旧模式间建立起联系，使完善的模式储存于学生的头脑中，从而为学生的灵活运用概念奠定基础.

【参考文献】

[1]曹才翰，章建跃.中学数学教学概论（第3版）[M].北京：北京师范大学出版社，2012.

[2] 徐文彬.数学概念的认识及其教学设计与课堂教学[J].课程·教材·教法，2010（10）：39-44.

[3]曹才翰，张建跃.数学教育心理学（第3版）[M].北京：北京师范大学出版社，2015.