填方工程中双排桩的设计方案优化

董金奎

(中煤第三建设(集团)有限责任公司， 宿州 234000)

双排桩通常由前排桩、后排桩、冠梁与横向连系梁组合而成，其具有较大的侧移刚度，施工工期短、施工简便且往往不需要内支撑,已被广泛应用于各类岩土工程中[1-3]。

目前，双排桩围护结构的设计计算理论尚不完善，通常采用基于Wenkler假定的弹性地基梁法及数值方法进行分析。《建筑基坑支护技术规程》(JGJ 120—2012)基于Wenkler假定的弹性地基梁法给出了双排桩的计算方法，但其仅适用于前后排桩对其、等距离、等桩长的情况[4]。

大量学者对双排桩的特性进行了广泛研究。顾亮[5]对基坑工程中双排桩支护结构在不同开挖阶段支护结构及岩土体的应力场、应变场、位移场的变化规律进行了深入探讨；王忠凯等[6]以葛洲坝城市花园二期工程项目基坑支护为例，对悬臂双排桩、双排桩锚两种支护结构的水平位移进行了监测，并模拟分析了桩顶连梁高度和排距对双排桩水平位移的影响规律；董妍[7]对某基坑工程双排灌注桩与两道预应力锚杆的支护结构进行了分析，基于监测数据与理论分析表明现有规范方法高估了后排桩的作用，建议适当增强桩间土传递土压力的作用，弱化后排桩抵抗变形的作用；彭文祥等[8]基于室内模型试验，对双排桩支护结构的最佳排距及结构内力进行了试验研究，分析了弯矩及桩顶位移的变化规律；张建文等[9]以成兰铁路九寨沟双线大桥为研究背景建立了双排桩支护结构的试验模型，结果表明后排抗滑桩和桥基之间有一个最佳距离，能起到充分减小桥基水平变形的作用；高阳等[10]基以济南市槐荫区某基坑工程的双排桩支护设计为例，分析了基坑、排桩不同位置的受力状态变化、位移变化过程，对各参数的敏感性进行了考察。这些研究促进了人们对双排桩受力特性的认识。

前人对双排桩研究与应用主要集中在挖方工程中，而对填方工程涉及较少。由于填方工程与挖方工程的施工工序完全不同，故即使双排桩的参数完全相同，在填方工程与挖方工程中桩体的受力也不尽相同，甚至区别非常大。若未认识到填方工程与挖方工程的施工区别，可能导致双排桩的设计出现较大偏差，甚至导致安全事故的发生。

为此，在分析填方工程双排桩施工特征的基础上，提出填方工程中双排桩腰部增设连系梁，以增强填筑过程中围护结构的整体性，并基于有限元法对比分析了新型双排桩与普通双排桩的受力区别，建议了填方工程中双排桩的合理构型，以便促进双排桩在填方工程中的合理应用。

1 填方工程双排桩的施工特性

在挖方工程中，一般先在指定位置开挖前排桩与后排桩的桩孔，再吊入钢筋笼并浇筑混凝土，后续在桩顶部支模、绑扎冠梁与横梁的钢筋再浇筑混凝土，最终形成双排桩。在双排桩混凝土强度满足规范要求后，再逐层进行基坑开挖。由于冠梁与横梁是在原地表(或下挖较浅深度处)进行作业，故挖方工程中双排桩的施工是较方便的。且挖方作业开始前，前排桩与后排桩已组合形成整体，具备较大的抗侧移刚度，为后续挖方作业提供了可靠的支护体系。

而对于填方工程，原地面以下的桩基础(锚固段)施工较方便，但地面以上双排桩需搭设脚手架支撑、支模、绑扎钢筋后浇筑混凝土施工，显然地面以上的支模是受到高度限制的。若地面以上桩体的长度较大，则无法一次性完成双排桩与其顶部的冠梁、横梁施工，往往需先施工双排桩的下部段、开展下部土层的填筑。待下部桩体范围内的填土完成后，再支模、续接钢筋笼对双排桩进行加长施工，再开展下一阶段填筑施工，如此循环，直至双排桩顶部的冠梁与横梁浇筑完毕，即前排桩与后排桩无法在填筑施工前组合形成整体。

显然，填方工程中的双排桩施工存在技术问题：前排桩与后排桩基本在最后填筑阶段才组合形成整体，而之前的下部填筑过程中各桩相互独立，处于悬臂状态，侧移刚度较小，土方填筑时容易发生较大的侧向位移。可见，在最后施工的桩顶冠梁与横梁组合之前，双排桩受到土压力已发生了较大变形，导致填方工程中的双排桩侧向位移可能无法满足工程需要。

鉴于此，提出填方工程可在双排桩的腰部(填土一半高度处)增设连系梁，使填方作业之前前排桩与后排桩已相互组合形成整体，即双排桩顶部的冠梁与横梁未施工之前其也具有较大的抗侧移刚度，从而能适应填方工程的需要。所提填方工程中腰部设置连系梁的双排桩施工方法如下。

(1)在前排桩、后排桩设计位置处，钻孔至设计标高，吊入钢筋笼、浇筑混凝土，施工形成原地面以下前排桩与后排桩的锚固段，该段桩体通常呈圆形，如图1(a)所示。

(2)在前一阶段混凝土强度满足规范要求后，续接钢筋笼、支模板、浇筑混凝土，形成前排桩、后排桩下部段及腰部连系梁，如图1(b)所示。

(3)待上一阶段混凝土强度满足规范要求后，分层填筑施工至腰部连系梁处，如图1(c)所示。前排桩之间可根据需要设置挡土板。

地面以下的抗滑桩通常采用机械旋挖，故呈圆形。而地面以上圆形模板难以实现(费用过高，且不方便连系梁钢筋绑扎)，为了支模方便，原地面以上的桩体通常呈矩形形状。

(4)续接钢筋笼、支模板、浇筑混凝土，形成前排桩、后排桩上部段及冠梁、顶部连系梁，如图1(d)所示。

(5)待混凝土强度满足规范要求后，分层填筑施工至桩顶处，完成填筑作业，如图1(e)所示。

2 有限元数值计算模型

现进一步基于有限元方法对比分析填方工程中有无腰部设置连系梁对双排桩受力的影响。

现以某填方工程[11]中双排桩为背景建立有限元数值分析模型。双排桩为C30圆形桩，直径 1.2 m、桩间距3.0 m；前后排桩排距4.0 m，桩顶部的冠梁与连系梁均采用C30混凝土，尺寸为1.2 m×0.8 m。填土高度11.0 m，双排桩原地面以下的锚固段长度9.8 m。

假定填方高度11.0 m范围内均采用双排桩，且在填方工程一半高度(5.5 m)处设置腰部连系梁，腰部连系梁与顶部连系梁的截面参数相同。采用Plaxis软件进行模拟，计算模型如图2所示。采用Mohr-Coulomb模型对土层进行模拟，土层的计算参数如表1所示。

数值计算按平面应变问题考虑，桩与连系梁均等效为板单元。假设围护桩桩径为D、桩中心距为L，按照抗弯刚度相等的原则等效为长度为L的板单元(相当于地下连续墙)，板单元的厚度h计算方法为

Lh3/12=πD4/64

(1)

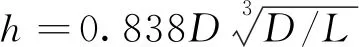
(2)

板单元的轴向刚度计算公式为

EA=EhL

(3)

板单元的抗弯刚度计算公式为

EI=ELh3/12

(4)

图1 填方工程中设置腰部连系梁双排桩的施工示意图Fig.1 Construction diagram of double row piles with waist connecting beam in filling engineering

式中：E为钢筋混凝土的弹性模量。等效后双排桩与连系梁的计算参数如表2所示。

有限元计算中采用如下假定。

(1)建模范围内，认为各土层呈均质水平层状分布，且同一土层为各向同性。

(2)填筑施工之前，可在已制作好桩体外围包裹多层塑料膜，达到降低甚至消除填土固结产生的负摩阻力的效果。该做法简单、廉价，能够有效消除负摩阻力的影响。故数值计算中，暂未考虑填方工程负摩阻力的影响。

(3)填筑施工之前，原地基土体的固结沉降早已完成。

有限元计算步骤如下。

第1步原土层自重应力平衡。

第2步初始位移归零，激活原土层中长度为9.8 m的双排桩锚固段。

第3步激活填土面以上长度为5.5 m的双排桩及腰部连系梁。

第4步分层填筑至高度5.5 m。

第5步激活上部长度为5.5 m的双排桩及顶部连系梁。

第6步分层填筑至高度11.0 m。

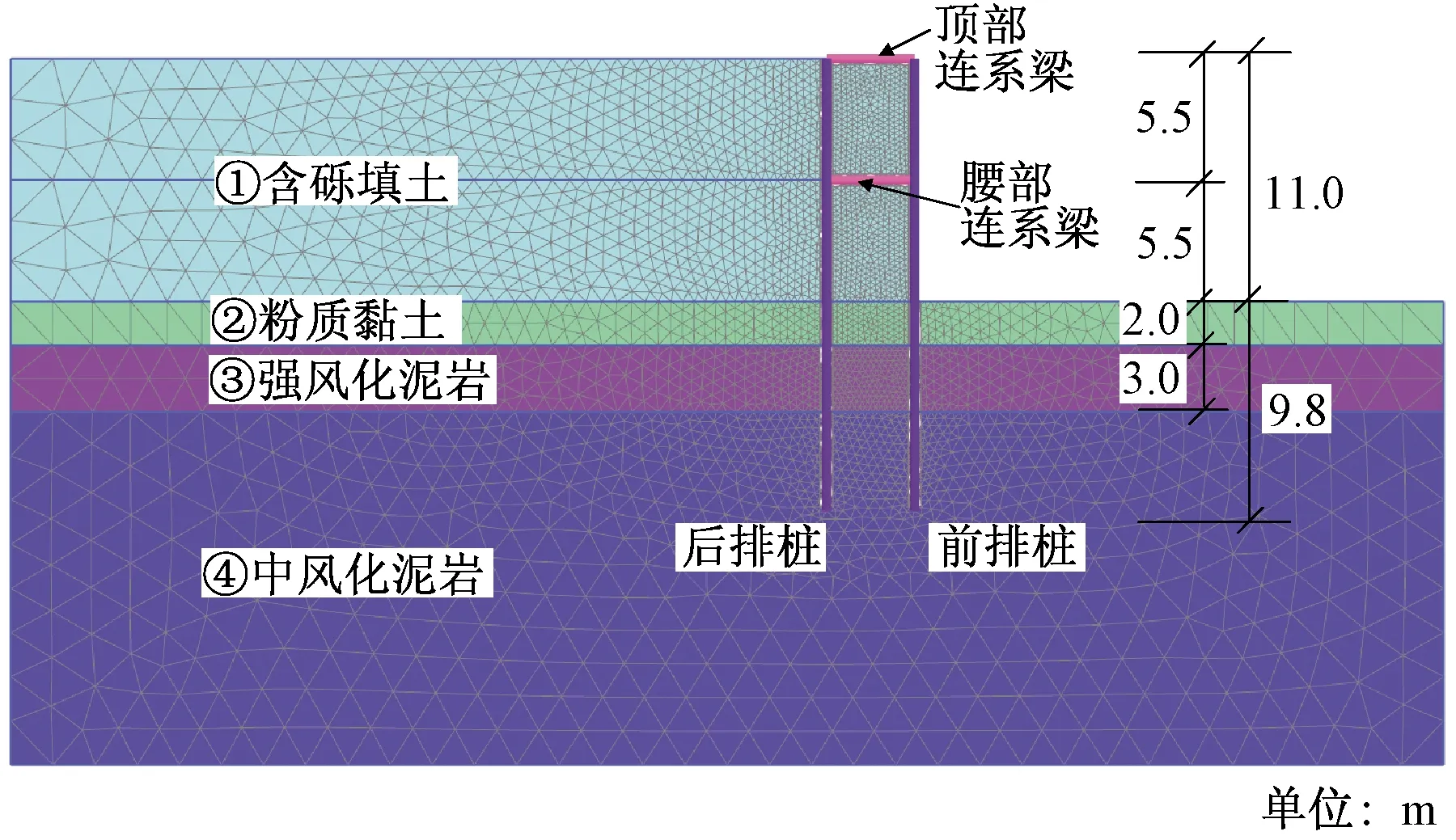
图2 有限元网格划分Fig.2 Finite element mesh

表1 土层计算参数

表2 板单元计算参数

第7步采用强度折减有限元计算填方工程的整体稳定性。

3 计算结果分析

填土总高度11.0 m，高度太大导致双排桩无法一次性施工到顶(否则脚手架与支模超出常规高度)，故可行的方案是分段施工双排桩、逐层填筑。

当双排桩不设腰部连系梁时，仅在上述第3步中不激活腰部连系梁即可。计算得到了设置/不设置腰部连系梁情况下，双排桩在各施工步骤的变形与受力情况。

3.1 填筑至5.5 m时

3.1.1 填土水平位移

填筑至总填方高度的一半时，双排桩未设置腰部连系梁时土体的水平位移最大值为9.2 mm，而设置腰部连系梁的土体水平位移最大值为4.9 mm。两种情况下的土体水平位移总体较小，主要原因是填土高度较小且抗滑桩悬臂段较短、刚度相对较大。但也可以看出，双排桩腰部设置连系梁后，土体的水平位移大大减小。

填筑至5.5 m时土体的水平位移等值线分布如图3所示，可见，水平位移最大值发生前排桩背面填土的中部附近。

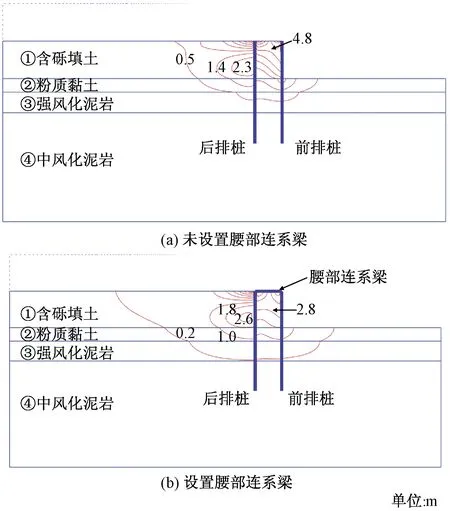
图3 填筑至5.5 m时土体水平位移等值线分布Fig.3 Isoline distribution of horizontal displacement of soil at filling to 5.5 m

图4进一步给出了填筑至5.5 m时前排桩与后排桩的水平位移情况。可见，未设置腰部连系梁时，前排桩的水平位移最大值位于桩顶处，其值为9.7 mm；后排桩的水平位移最大值也位于桩顶处，其值为3.9 mm；前排桩的水平位移远大于后排桩的水平位移。此时的前排桩与后排桩均为悬臂状态，前排桩与后排桩各自独立变形，且前排桩承担后大部分的土压力(前排桩之间一般设置挡土板)，故前排桩的水平位移大于后排桩的相应值。

而设置腰部连系梁后，前排桩与后排桩的水平位移相差不大，前排桩与后排桩的水平位移最大值位于桩顶且相等，其值为3.2 mm。可见，腰部设置连系梁可大大降低桩体的水平位移，前排桩的水平位移减小幅度达到67.0%。

3.1.2 桩体内力

填筑至5.5 m时前排桩与后排桩的轴力分布如图5所示。未设置腰部连系梁时，前排桩与后排桩的轴力最大值(绝对值)分别为124.8、277.8 kN/m；设置腰部连系梁后，前排桩与后排桩的轴力最大值(绝对值)分别为179.3、239.7 kN/m。可见，设置腰部连系梁后，前排桩轴力最大值增大了43.7%，而后排桩轴力最大值减小了13.7%。但总体上这些轴力偏小，桩基础能承受较大的轴力，故该轴力不会成为桩基础设计的控制荷载。

填筑至5.5 m时前排桩与后排桩的剪力分布如图6所示。未设置腰部连系梁时，前排桩与后排桩的剪力最大值(绝对值)分别为77.5、57.2 kN/m；设置腰部连系梁后，前排桩与后排桩的剪力最大值(绝对值)分别为64.4、54.5 kN/m。可见，设置腰部连系梁后，前排桩剪力最大值减小了16.9%，后排桩剪力最大值减小了4.7%。

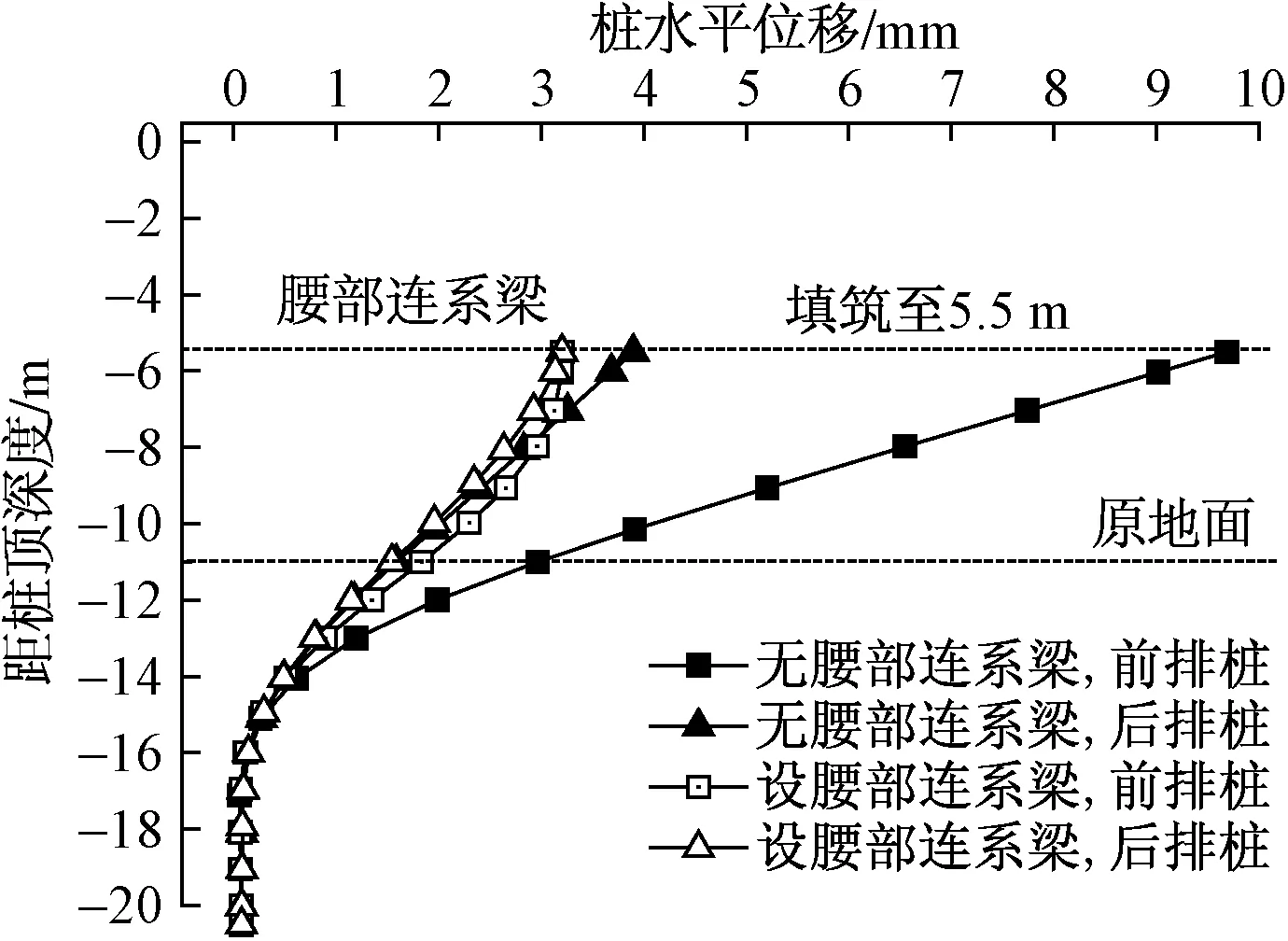
图4 填筑至5.5 m时双排桩水平位移Fig.4 Horizontal displacement of piles at filling to 5.5 m

图5 填筑至5.5 m时桩的轴力Fig.5 Axial force of piles at filling to 5.5 m

填筑至5.5 m时前排桩与后排桩的弯矩分布如图7所示。未设置腰部连系梁时，前排桩与后排桩的弯矩最大值(绝对值)分别为243.7、97.2 kN·m/m；设置腰部连系梁后，前排桩与后排桩的弯矩最大值(绝对值)分别为114.5、125.8 kN·m/m。可见，设置腰部连系梁后，前排桩弯矩最大值减小了53.0%，后排桩弯矩最大值增加了29.4%。

图6 填筑至5.5 m时桩的剪力Fig.6 Shear force of piles at filling to 5.5 m

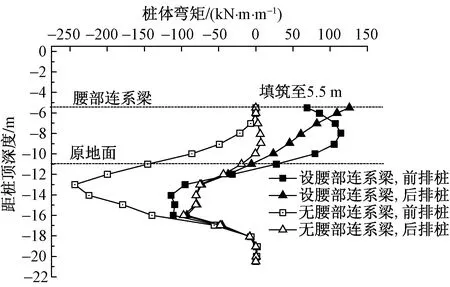
图7 填筑至5.5 m时桩的弯矩Fig.7 Bending moment of piles at filling to 5.5 m

3.2 填筑至11.0 m时

3.2.1 填土水平位移

填筑竣工即填筑至11.0 m时，双排桩未设置腰部连系梁时土体的水平位移最大值为35.7 mm，而设置腰部连系梁的土体水平位移最大值为 18.3 mm。设置腰部连系梁使填土水平位移最大值减少48.7%，可见其对约束填土变形具有较大作用。

填筑至11.0 m时土体的水平位移等值线分布如图8所示，可见，双排桩未设置腰部连系梁时土体的水平位移最大值位于前排桩背面填土的中上部，设置腰部连系梁后土体的水平位移最大值位于腰部连系梁附近。而在挖方工程中，坑壁水平位移最大值往往位于桩顶处。

图9进一步给出了填筑至11.0 m时前排桩与后排桩的水平位移情况。未设置腰部连系梁时，前排桩与后排桩的水平位移最大值位于桩顶处且相等，其值为33.2 mm；设置腰部连系梁后，前排桩与后排桩的水平位移最大值位于桩顶处且相等，其值为16.8 mm。设置腰部连系梁使前后排桩水平位移最大值减少49.4%，可见其对约束桩体变形具有较大作用。设置腰部连系梁后，前排桩与后排桩沿深度方向的水平位移基本一致，说明腰部连系梁使前后排桩组合形成稳定的空间结构。

3.2.2 桩体内力

填筑至11.0 m时前排桩与后排桩的轴力、剪力与弯矩分布如图10～图12所示。可见，腰梁以上与腰梁以下的桩体内力发生较大变化，为了分析方便，对前排桩与后排桩的内力分段对比，如表3、表4所示。表3、表4中轴力、剪力与弯矩值均为指定范围内绝对值的最大值；增幅指腰部设置连系梁梁相对于腰部无连系梁时的变化，负值表示减小，正值表示增加。

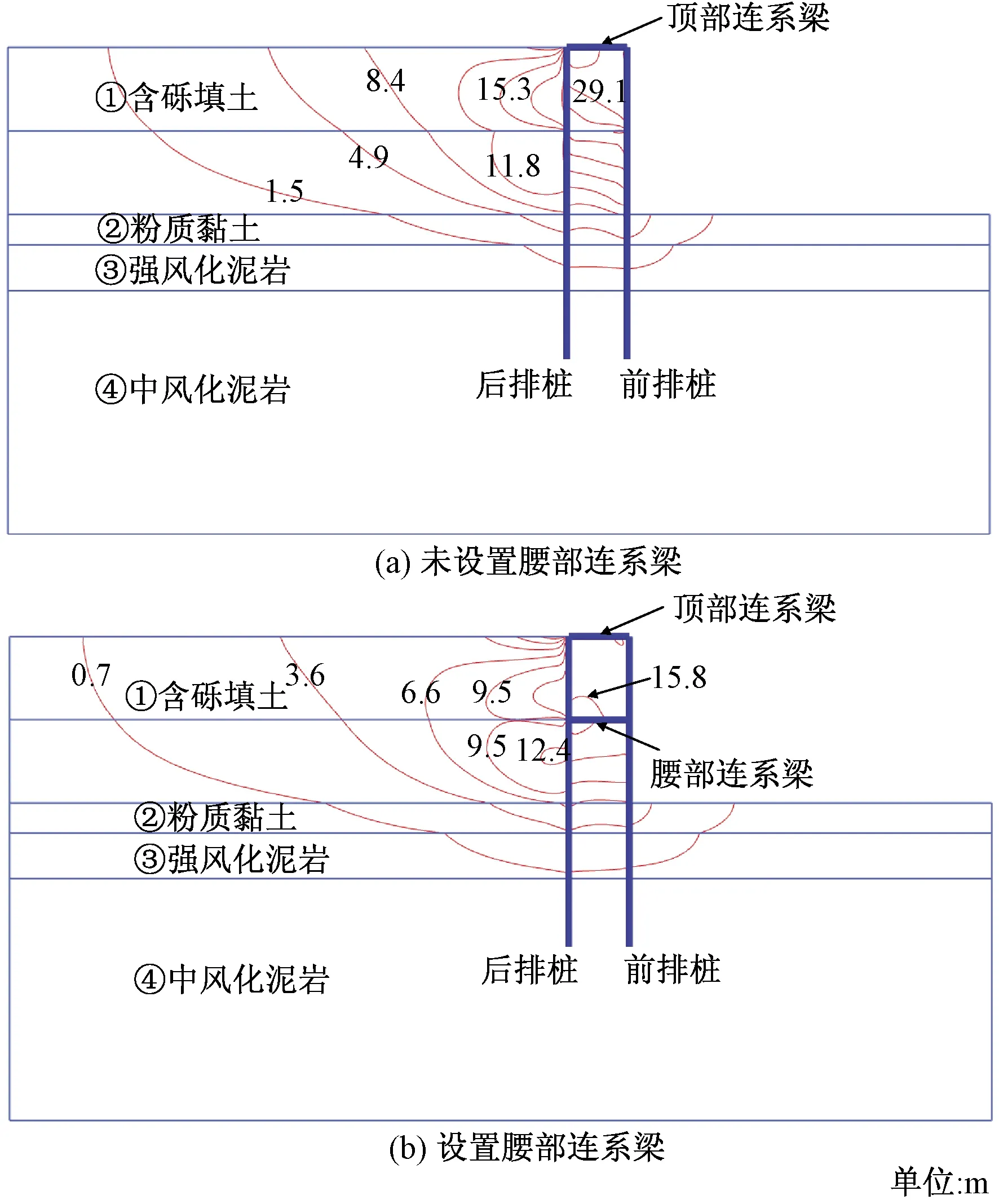
图8 填筑至11.0 m时土体水平位移等值线分布Fig.8 Isoline distribution of horizontal displacement of soil at filling to 11.0 m

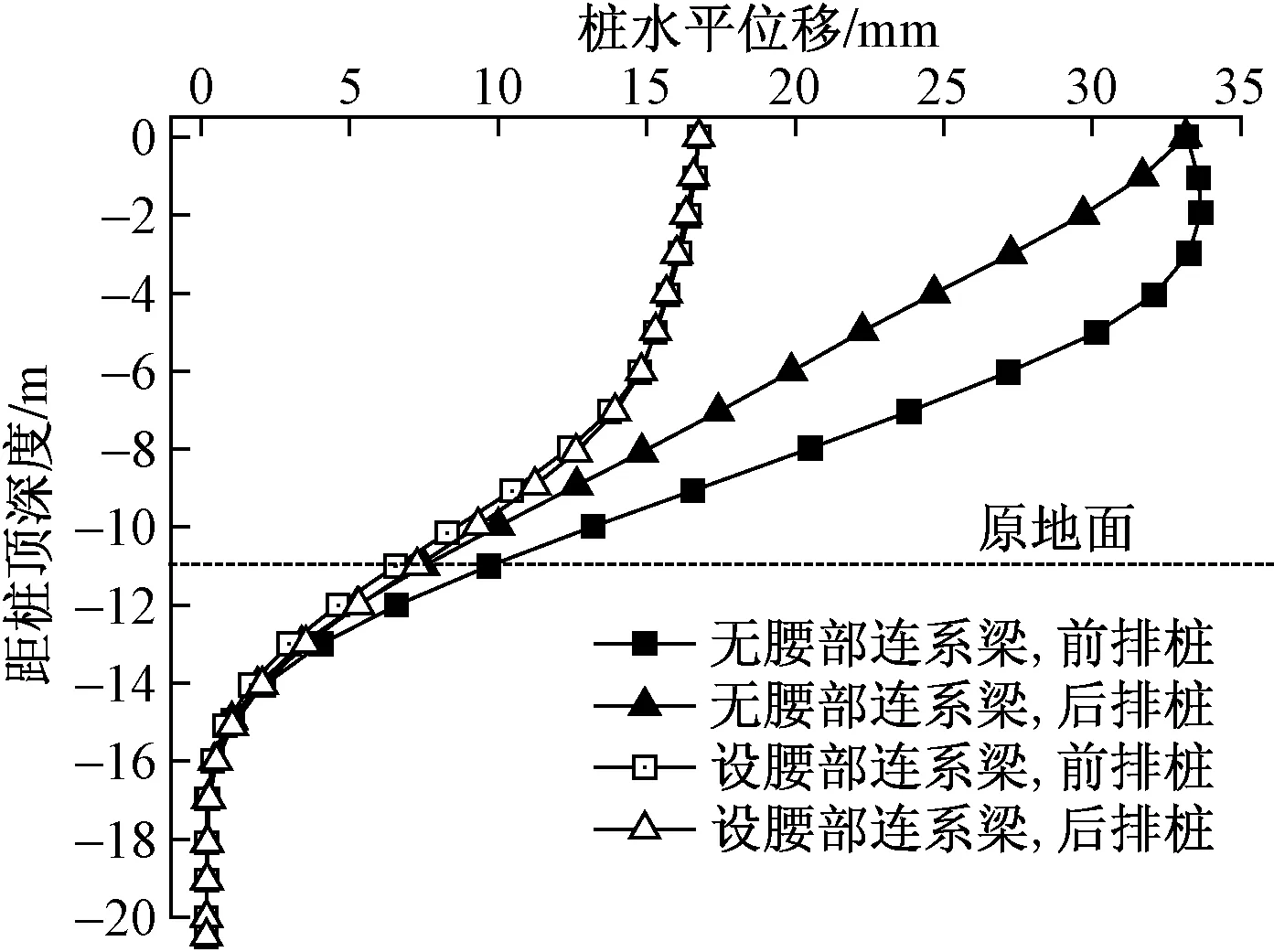
图9 填筑至11.0 m时双排桩水平位移Fig.9 Horizontal displacement of piles at filling to 11.0 m

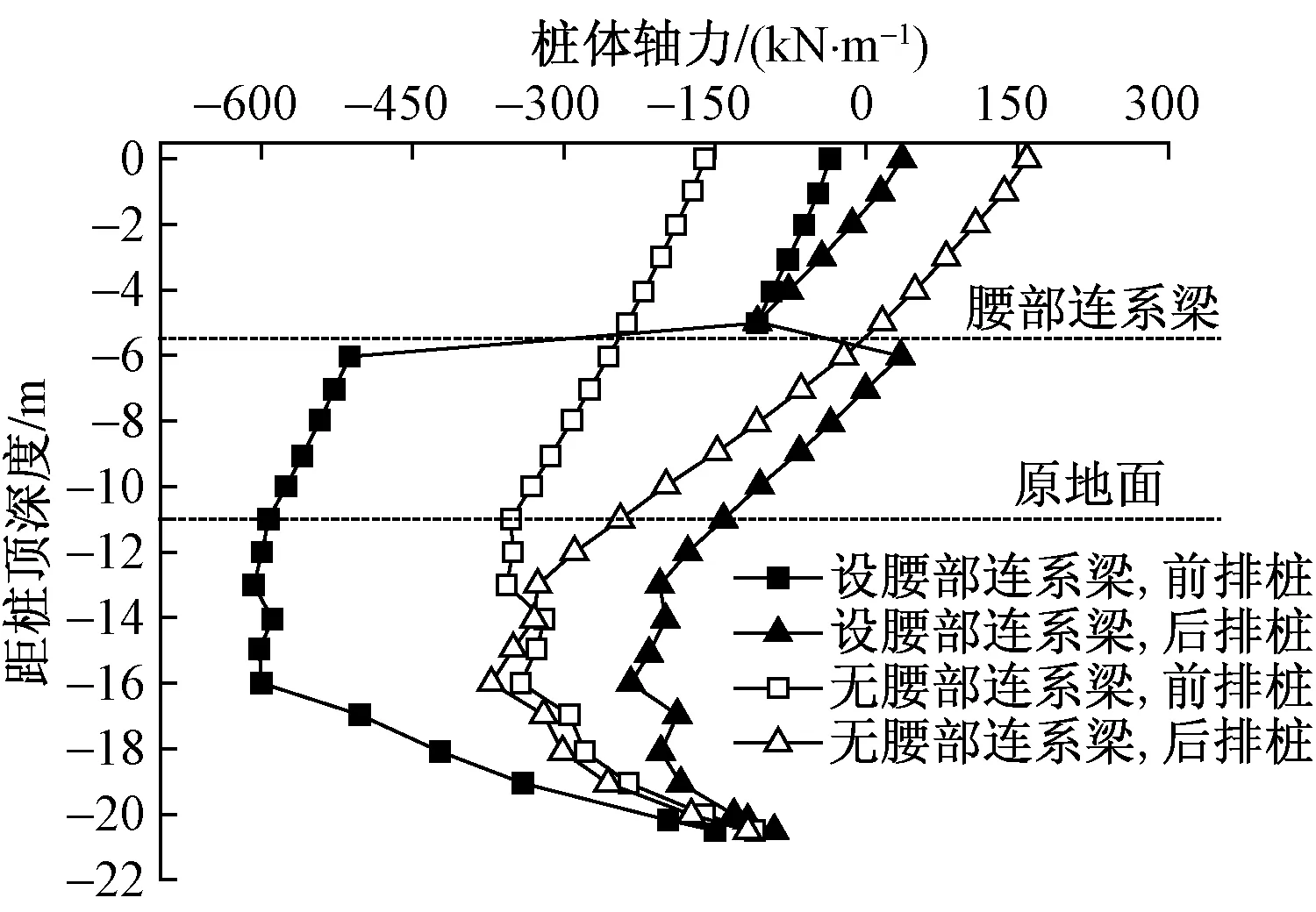
图10 填筑至11.0 m时桩的轴力Fig.10 Axial force of piles at filling to 11.0 m

图11 填筑至11.0 m时桩的剪力Fig.11 Shear force of piles at filling to 11.0 m

图12 填筑至11.0 m时桩的弯矩Fig.12 Bending moment of piles at filling to 11.0 m

(1)腰部设置连系梁后，腰部连系梁以上前排桩与后排桩的轴力、剪力与弯矩最大值均变小，其中弯矩的降幅超过75%。

(2)腰部设置连系梁后，腰部连系梁以下前排桩与后排桩的剪力与弯矩最大值均变小，其中弯矩的降幅超过10%。

(3)腰部设置连系梁后，腰部连系梁以下前排桩的轴力大幅度增加、后排桩的轴力大幅度减小。

(4)设置腰部连系梁对前排桩与后排桩的剪力与弯矩具有均化作用，即使桩身范围内剪力与弯矩的最大值减小、分布更均匀。

3.2.3 连系梁内力

腰部设置连系梁对桩顶连系梁内力的影响如表5所示。可见，腰部设置连系梁后，桩顶连系梁的轴力、剪力与弯矩大幅度减小，其中弯矩的降低幅度达到77.9%。

腰部设置连系梁后，腰部与桩顶连系梁内力的比较如表6所示。可见，腰部与桩顶连系梁所受轴力均非常小。桩顶连系梁的剪力与弯矩与腰部连系梁相比均非常小，取值均小于腰部连系梁相应值的15%。

3.3 填方工程稳定性

基于强度折减有限元法[12-14]，对填方工程竣工的稳定性进行分析，得到土体滑裂面位置如图13所示。可见，滑裂面底部穿过双排排桩原地面以下2.0 m深度处。

对比计算表明，双排桩腰部设置横梁与否对填方工程的滑裂面位置及安全系数影响非常小，基本可以忽略不计。在抗滑桩本身强度足够的情况下，填方工程的稳定性取决于锚固段的长度，腰部设置横梁虽然可以加强双排桩的整体性，但其穿过下部土层的滑裂面位置及长度影响有限，进而对安全系数的影响也非常小。

表3 腰部设置连系梁对前排桩内力的影响分析

表4 腰部设置连系梁对后排桩内力的影响分析

表5 腰部设置连系梁对桩顶连系梁内力的影响分析

表6 腰部连系梁与桩顶连系梁的对比分析

图13 填方工程失稳破坏时的滑裂面位置Fig.13 Failure slip surface at failure of fill engineering

4 填方工程双排桩的受力特征

对比分析了腰部设置连系梁与否对土体变形与桩体内力的影响，基于这些规律可对填方工程的双排桩进行优化设计。

4.1 关于桩身轴力的分析

根据建筑地基基础设计规范第8.5.9条[15]，直径1.2 m、桩间距3.0 m的桩身混凝土能够承担的轴力计算如式(5)所示：

Q=Apfcψc/L=(π×0.62×14.3×103×0.6/3) kN/m=3 234.5 kN/m

(5)

式(5)中：Q为桩身混凝土的轴力承载力(每延米)；Ap为桩身截面积；fc为混凝土轴心抗压强度设计值；ψc为工作条件系数(取0.6)；L为桩间距。

可见，双排桩能够承担轴力3 234.5 kN每延米，而表3、表4中的轴力最大值为607.6 kN每延米，桩体所受最大轴力仅为轴力承载力的18.9%。可见，抗滑桩设计中，轴力不是控制荷载，基本可以忽略不计，这与已有设计经验是吻合的。故表3、表4 中所示轴力远小于桩体的轴力承载力，轴力的增减对双排桩基本无影响，有无腰部连系梁时前排桩与后排桩的轴力承载力均能自动满足要求。

4.2 关于桩身剪力的分析

根据《混凝土结构设计规范》(GB 50010—2010)第6.3.1条[16]，桩体的剪力承载力估算如式(6)所示：

V=0.2βcfcbh0/L=(0.1×1.0×14.3×

103×0.5×π×0.62/3) kN/m=

2 695.4 kN/m

(6)

式(6)中：V指抗滑桩的抗剪承载力(每延米)；βc为混凝土强度影响系数；bh0指有效截面面积，暂按桩横截面积的1/2估算。

可见，各单桩能够承担剪力2 695.4 kN每延米，而表3、表4中的剪力最大值为248.5 kN每延米，桩体所受最大剪力仅为剪力承载力的9.2%。可见，抗滑桩设计中，剪力不是控制荷载，基本可以忽略不计，可按构造配置箍筋，这与已有设计经验是吻合的。表3、表4中所示剪力值远小于桩体的剪力承载力，剪力的增减对双排桩基本无影响，有无腰部连系梁时前排桩与后排桩的剪力承载力均能自动满足要求。

4.3 腰部设置连系梁的经济性分析

根据上述分析，桩基础中轴力与剪力均不是控制荷载，桩基础的截面面积与配筋显然取决于弯矩，弯矩的大小成为桩基础的经济技术指标，弯矩大则桩径大、配筋高，造价也相对较高；弯矩小则桩径小、配筋低，造价也相对较低，这符合已有的设计经验。虽然弯矩变化与造价变化之间的精确计算较复杂，但不妨就按弯矩的变化幅度简单等效为造价的变化幅度进行粗略分析，则由表3、表4数据可得到腰部增设连系梁后桩体的弯矩变化情况，如表7 所示。

由表7可见，双排桩设置腰部连系梁后，前排桩、后排桩、顶部连系梁的弯矩降低故造价也会降低，其中腰部连系梁以上的前排桩、后排桩、顶部连系梁的弯矩降幅超过75.0%。腰部连系梁以上桩长5.5 m，顶部连系梁长度4.0 m，即设置腰部连系梁后单跨累计长度为15.0 m(5.5 m+5.5 m+4.0 m)的桩体弯矩降低了75.0%以上，而代价仅是增加了长度4.0 m腰部连系梁，显然总体造价是大幅度降低的。

表7 腰部增设连系梁对桩弯矩的影响

再结合上述变形规律，腰部设置连系梁可降低桩体水平位移达到67.0%，可见，填方工程中腰部设置连系梁是经济合理且非常必要的。

5 填方工程双排桩优化设计

根据表7数据可知，腰部增设连系梁后，腰部连系梁以上的双排桩及顶部连系梁的控制荷载大大减小，说明上部结构的强度与刚度已过剩。可否对双排桩上部进行优化设计，以省去桩顶连系梁及前排桩上部段。

对该问题进行对比分析，为此建立如图14所示的计算模型，原地面以上前排桩的高度仅为后排桩高度的1/2，前排桩顶部设置冠梁，同标高处的后排桩处设置腰梁，在前排桩的冠梁与后排桩腰梁之间设置连系梁，该连系梁相当于传统双排桩的顶部连系梁。

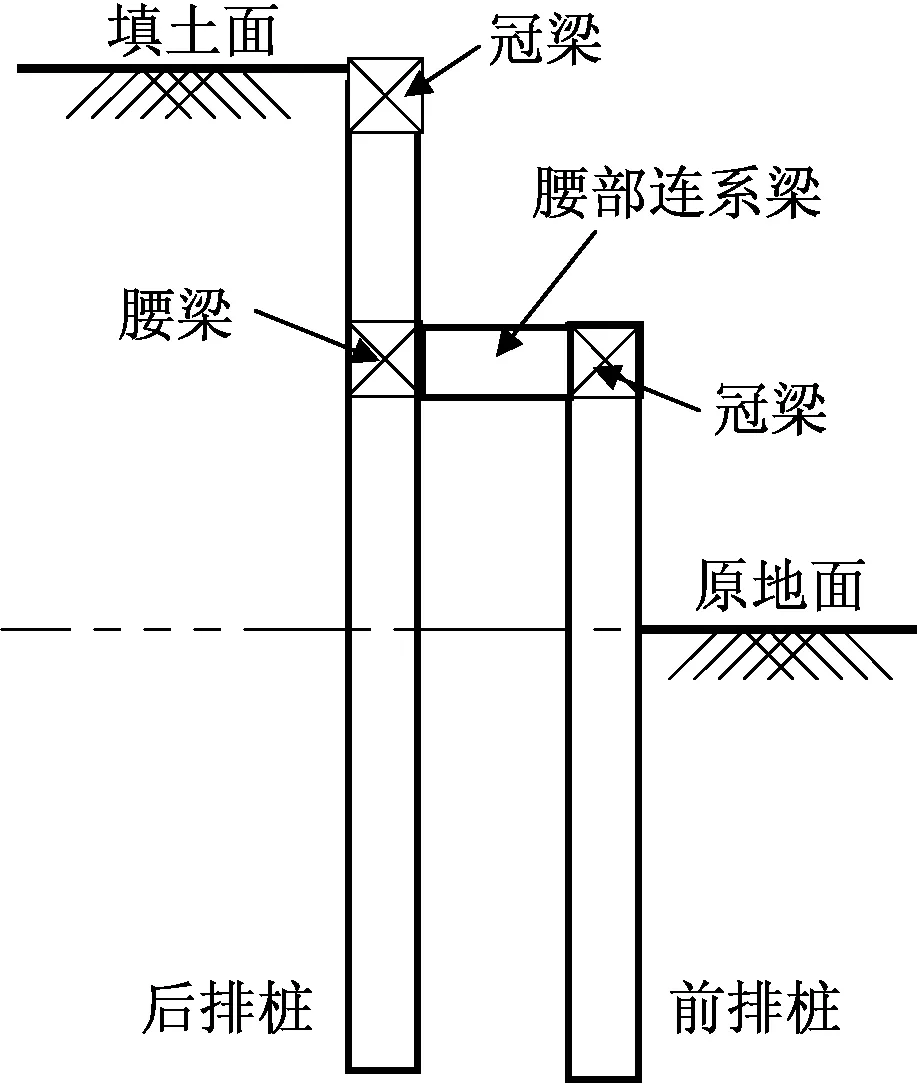
图14 填方工程双排桩优化设计方案Fig.14 Optimal design of double row piles in filling engineering

5.1 变形情况

基于有限元方法计算得到，填方工程竣工时土体的水平位移最大值为20.8 mm，比前文计算得到的传统双排桩减小了41.7%，比腰部增设连系梁(图2模型)的情况增加了13.7%，仍在规范允许范围内。

填筑至11.0 m时土体的水平位移等值线分布如图15所示，可见，土体的水平位移最大值位于连系梁附近。

填筑至11.0 m时前排桩与后排桩的水平位移情况如图16所示，后排桩的水平位移最大值发生在桩顶处，其值为19.4 mm，比计算得到的传统双排桩减小了41.6%，比腰部增设连系梁(图2)的情况增加了15.5%。

可见，就土体与抗滑桩的变形而言，图14所示的优化方案比传统双排桩结构更能约束填土的变形，能够满足工程需要。

5.2 桩体内力

进一步得到了优化方案的双排桩内力分布情况。鉴于轴力与剪力通常不是填方工程桩基础的控制荷载，此处仅分析弯矩情况，如图17所示。

前排桩的弯矩绝对值最大值为632.8 kN·m/m，后排桩腰部连系梁以下的弯矩绝对值最大值为454.4 kN·m/m，后排桩腰部连系梁以上的弯矩绝对值最大值为144.0 kN·m/m。而传统双排桩设计中，前排桩的弯矩绝对值最大值为731.3 kN·m/m，后排桩的弯矩绝对值最大值为485.7 kN·m/m。图14所示的连系梁弯矩最大值639.7 kN·m/m，而图2所示的腰部连系梁弯矩最大值651.7 kN·m/m，两者基本相当。可见，图14所示的优化方案比传统双排桩结构的弯矩均有所减少，特别是腰部连系梁以上后排桩的弯矩减小幅度达到70.3%，显然受力更合理。

图15 优化方案的土体水平位移等值线分布Fig.15 Isoline distribution of horizontal displacement of soil with optimal design of double row piles

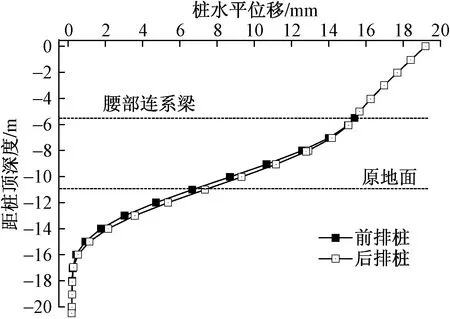
图16 双排桩优化设计方案桩体水平位移分布Fig.16 Horizontal displacement of piles with optimal design of double row piles

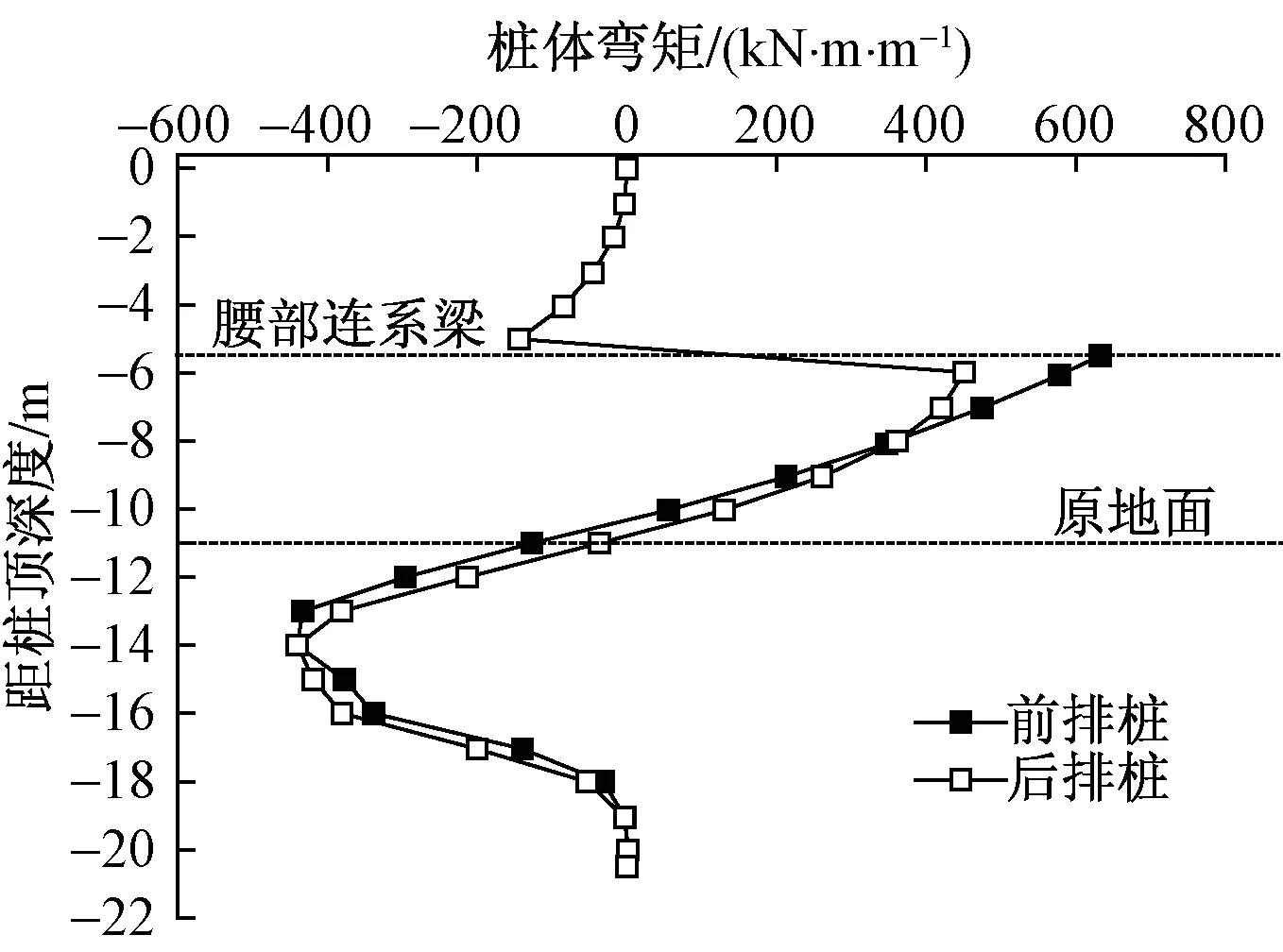
图17 双排桩优化设计方案桩体弯矩Fig.17 Bending moment of piles with optimal design of double row piles

5.3 填方工程稳定性

基于强度折减有限元法计算得到填方工程的安全系数为2.08，土体滑裂面位置如图18所示。可见，上部双排桩构型的变化对滑裂面的形状与位置基本无影响。由于本工程双排桩的锚固段长度较大，且下部土层为强风化泥岩与中风化泥岩，土体强度相对较高，故所提三种双排桩方案的稳定性基本相同。

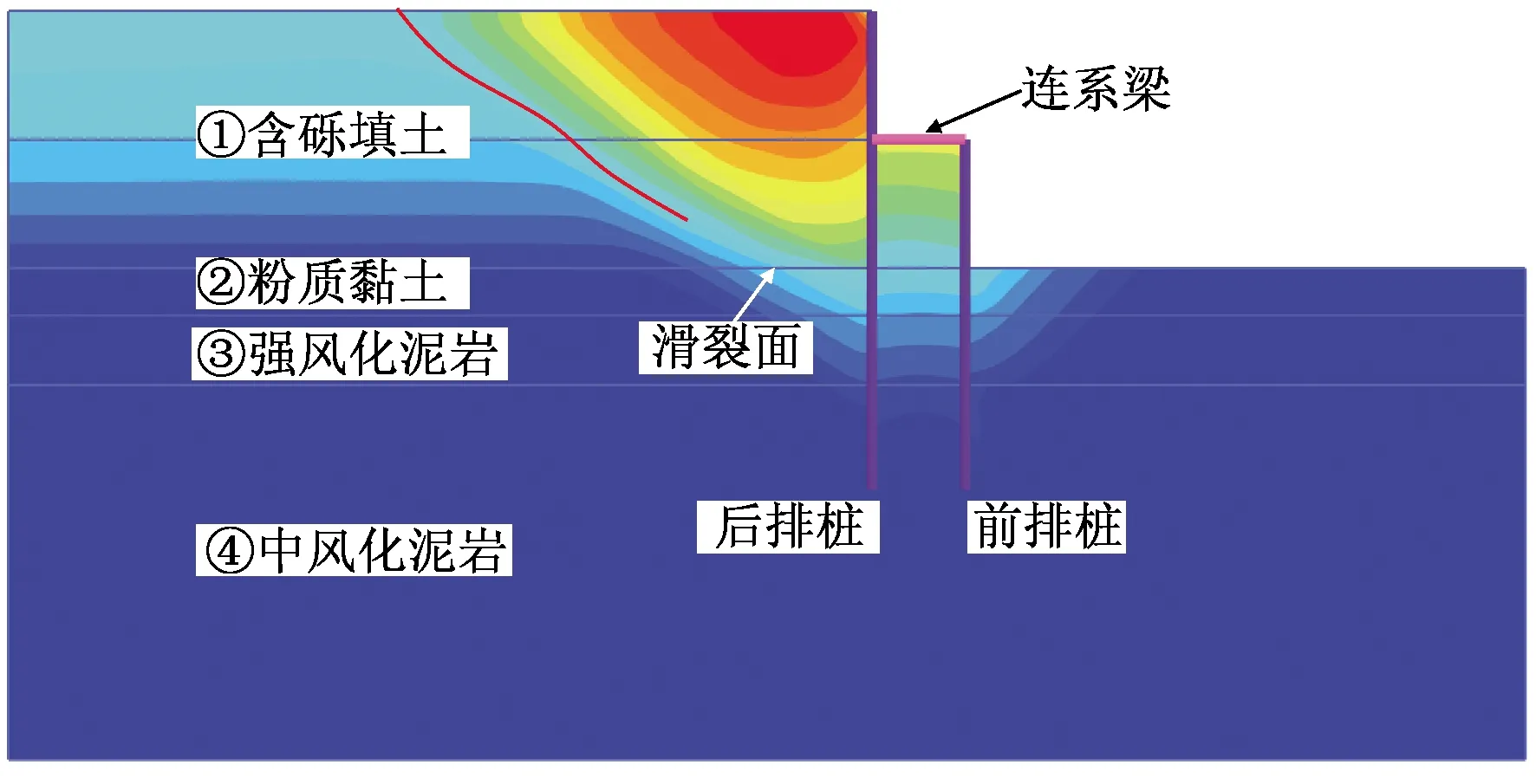
图18 双排桩优化设计方案土体滑裂面Fig.18 Failure slip surface of fill engineering with optimal design of double row piles

5.4 优化构型的确定

根据上述分析，可确定填方工程中双排桩的最终优化方案，如图19所示。该双排桩优化方案的特征如下。

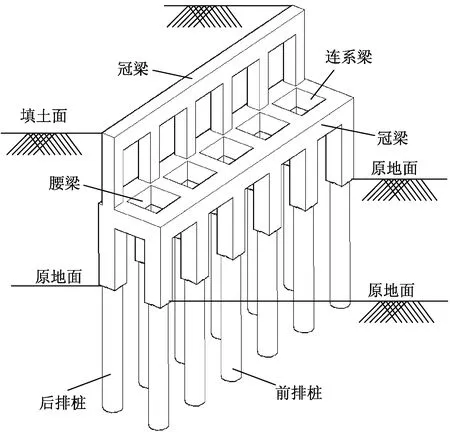
图19 填方工程双排桩优化方案三维示意图Fig.19 3D diagram of optimization scheme of double row piles in filling engineering

(1)原地面以下的桩基钻孔采用机械进行旋挖，故呈圆形；而原地面以上的双排桩及连系梁采用脚手架支撑、模板支护形成，故呈矩形形状。

(2)原地面以上前排桩短、后排桩长，地面以上后排桩的高度即为填土高度。地面以上前排桩的长度可取后排桩长度的1/2。

(3)前排桩与后排桩的顶部均设置冠梁，在与前排桩冠梁标高相同位置处的后排桩设置腰梁，前排桩的冠梁与后排桩的腰梁之间设置连系梁。该连系梁可连续分布，也可间隔分布。

(4)由于弯矩控制荷载区别较大，后排桩腰梁以上的截面尺寸小于腰梁以下的截面尺寸，相应配筋也减小，达到降低造价的效果。

(5)原地面以上的双排桩之间、腰梁以上的后排桩之间设置挡土板(图19中未画出)。

与传统双排桩方案相比，填方工程中图19所示的双排桩优化方案的总桩长更小，用料更少，土体变形更小，具备合理性与可行性，所提构型值得设计人员重视。

上述分析是基于二维有限元完成的，简化与假定导致其计算结果与实际情况可能存在一定的差距，后续尚有待进一步开展模型试验、现场试验与三维有限元论证，以期促进双排桩在填方工程中的合理运用。限于篇幅，未对连系梁的特性进行分析。

6 结论

(1)由于填方工程与挖方工程中双排桩的施工工序不同，导致填方工程中横向连系梁施工滞后、前排桩与后排桩无法尽早组合形成整体，桩体在悬臂状态下进行一定高度的土方填筑，造成最终土体的变形较大。填方工程中，可在前排桩与后排桩的腰部增设连系梁，使填筑作业尚未开始前前排桩与后排桩已组合形成整体，提高了施工过程中双排桩的侧移刚度。

(2)数值计算表明，双排桩腰部增设连系梁后，填方工程中填土与桩体的水平位移大大减小，降幅超过45%。

(3)填方工程的双排桩设计中，轴力与剪力往往不是控制荷载，桩基础的截面与配筋取决于弯矩。填方工程双排桩腰部增设连系梁后，前排桩、后排桩、顶部连系梁的弯矩均发生降低，其中腰部连系梁以上的前排桩、后排桩、顶部连系梁的弯矩降幅超过75.0%。

(4)鉴于腰部连系梁以上构件的弯矩大大减小，可对填方工程的双排桩进一步优化，使原地面以上前排桩的高度仅为后排桩高度的1/2，前排桩顶部设置冠梁，同标高处的后排桩处设置腰梁，在前排桩的冠梁与后排桩腰梁之间设置连系梁。

(5)数值计算表明，优化后双排桩方案的填土水平位移与桩体控制内力比传统双排桩方案的相应值更小，说明优化方案是可行的。特别地，优化方案中后排桩腰梁以上的截面尺寸小于腰梁以下的截面尺寸，相应配筋也减小，以达到降低造价的效果。