中医学数学模型的构建与应用

张芮宁, 张 阳

(1.山东潍坊人民医院, 山东 潍坊 261000; 2.中国科学院中科建设山东东润清洁能源有限公司, 山东 东营 257000)

中医是在我国流传发展了几千年的传统医学。从《黄帝内经》到后来的《伤寒论》《温病论》等著名中医论著,由于都没有数学方法和公式,因此，在崇尚定量分析和数学描述的西方人看来,中医神秘莫测。其实中医学中也有数学,中医学一直认定养生保健以“法于阴阳,和于术数”为原则,中医学理论也是数的“阳奇阴偶”及“象为主,数为用”的数学抽象象征的体现。如果中医能够用数学方法描述,进而与现代信息技术、人工智能相结合,那么中医的研究与应用将为人类的文明与进步其作出更大的贡献。从脑科学的角度看,人工智能与大数据、区块链、云计算、工业互联网之间的关系[1-4],可以衍生各种复杂数据计算,但是大体量的数据拓扑图线路繁杂且不便于观察[5-9],这些数据的内容,包括数量、速度等也呈现了不断增长的复杂性,而网络图的数学模型可以给中医学数据计算提供清晰的逻辑关系[10-13],故构建中医学数学模型就显得尤为重要。文章运用环型、树型、网状结构分支分层构建中医学数学模型,将中医学中错综复杂而又难以解决的问题分层次降解,形成有序的分支层次结构，使中医学数学模型人工智能化。

1 模型的构建

1.1 网络拓扑中医学数学模型

一层包括：中医理论x(1)、病因病机x(2)、四诊x(3)、辩证方法x(4)、防治治疗x(5)；

二层包括：元气论x(1,1)、阴阳学说x(1,2)、五行学说x(1,3)、藏象学说x(1,4)、病因x(2,1)、病机x(2,2)、望珍x(3,1)、闻诊x(3,2)、问诊x(3,3)、切诊x(3,4)、八纲辩证x(4,1)……卫气营血辩证x(4,4)、防治x(5,1)、治法x(5,2);

三层包括：养生预防x(5,1,1)……三因制宜x(5,1,6)、汗法x(5,2,1)……消法x(5,2,9);

四层包括：中药x(5,1,1,1)、方剂x(5,1,1,2)、针灸x(5,1,1,3);

五层包括：解表药x(5,1,1,1,1)……外用药x(5,1,1,1,18)、解表剂x(5,1,1,2,1)……外用剂x(5,1,1,1,2,18)、针灸疗法x(5,1,1,3,1)……拔罐疗法x(5,1,1,1,3,4)。

对于复杂的中医学数学模型来说,可能有多种结构类型,图1的一层为环型结构,二层和三层为树型结构,四层为网状结构,五层为树型结构。这几种结构类型都可用一种数学矩阵表示如下:

从上式得到一层中医学数学模型:

(1)

由上式推导出2层中医学数学模型数学公式为：

(2)

由此可推出n层中医学数学模型数学公式为:

(3)

注:(i, …,i)为n层所有集数。

由式(1)(2)(3)推导全网络中医学数学模型数学公式为:

(4)

此公式可反向表述即：

1.2 人工智能神经中医学数学模型

人工智能网络是由大量神经元按照大规模并行的方式通过一定的拓扑结构连接而成的网络。目前使用最广泛的是BP神经网络和它的变化形式。

BP人工智能神经中医学数学模型代入公式(4)，简化为：

推导出BP人工智能神经中医学数学模型公式为

(5)

2 模型的求解

2.1 中医学数学模型的分解合并公式

中医学数学模型经常需要精简点或需要增加点,图2是单层中医学数学模型发生减少的拓扑图。

中医学数学模型减少一个点公式推导如下:

对应的,单层中医学数学模型增加一个点模型结果为:

同理,可推导多层中医学数学模型的分解和合并模型:

(6)

其中: (k≥0)为所有层可增减中医学数学模型集数。

2.2 中医学数学模型运转效率数学公式

中医学数学模型运转效率用比率V来表示,又称中医学数学模型缩放比,由图2可建立一个单层缩放比公式：

n层中医学数学模型的缩放比公式为:

(7)

从缩放比公式可知,缩放比值越大，中医学数学模型运转效率越高。将中医学数学模型运转效率公式运用于数据网络会变成中医学数学模型实时动态图。

2.3 中医学数学模型数学逻辑地址

用中医学数学模型表示数学逻辑地址,比较清晰简洁。得到数学逻辑地址表示如图1,中医学数学模型x(5,1,1,1,1)(中药)数学逻辑地址表示式如下:

得到中医学数学模型逻辑地址公式为:

(8)

本中医学数学模型的数学逻辑地址特点是表示简单,可以无限扩充。

2.4 中医学数学模型的乘法推导公式

由中医学数学模型加减法推导出中医学数学模型乘法公式:

注:中医学数学模型加减法及乘法是与对应原数学模型相加减乘。

2.5 中医学数学模型的特征向量和特征值

(10)

将公式(9)(10)代入特征向量与特征公式得：

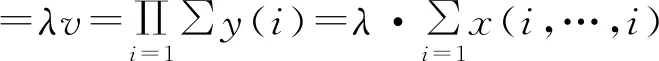
(11)

2.6 中医学的深度学习数学模型

整个神经网络的计算可以用矩阵式给出。每层的神经元个数不一样,输入输出维度、计算式中的矩阵和向量的行列数也就不一样,但形式是一致的。假设考虑的这一层是第i层，它接受m个输入,那么这一层的计算如下式:

(12)

从中医学数学模型的特征向量和特征值式(9)代入式(12)得到中医学的深度学习数学模型:

(13)

3 模型的应用

中医学人工智能简单说就是用一种算法允许计算机通过合并新的数据来学习,模拟人的思维、信息的分布形式和并行方式来进行协同处理,根据逻辑规则来进行推理的过程。这种思维是将分布式存储的信息综合起来所产生的想法或解决问题的办法。如下案例:

吴某某,男,44岁。2019年6月5日初诊。低热2月有余,曾做西医检查,找不出病因、病灶,每日只注射生理盐水、抗生素、激素等药物,治疗2月仍无效。刻诊情况如下:患者自觉头痛,体温37.5°C,纳可(胃口可以,不好不坏),眠可(睡眠正常),二便正常,脉象稍弦细,别无异常。《伤寒论》云:“伤寒脉弦细,头痛发热者,属少阳。”

病因为风寒发热即:x(2,1,1)

切诊为脉弦细即:x(3,4,12)

属少阳指六经辩证里的太阳、阳明、少阳、太阴、少阴和厥阴的少阳。即x(4,3,3)

将上列数据代入公式(5)得到图3。

由机器学习输入x(2,1,1)、x(3,4,12)、x(4,3,3),得到输出x(5,1,1,2,1,7)，即中药方剂:柴葛解肌汤;x(5,1,1,1,1,3)，即中药:柴胡;x(5,1,1,3,3,11)，即针灸:足少阳胆经。

将这三种中医方法代入中医学深度学习公式(13)得到下式：

经过计算层次总排序权值和一致性检验,柴葛解肌汤x(5,1,1,2,1,7)对总目标的权值为:

0.8×0.32+0×0.36+0.3×0.32=0.37

同理得柴胡x(5,1,1,1,1,3)、足少阳胆经x(5,1,1,3,3,11)对总目标的权值为0.78、0.29。

由此看出x(5,1,1,1,1,3)>x(5,1,1,2,1,7)>x(5,1,1,3,3,11),中药柴胡效果最好。

由临床中医老医师诊断依据中医六经治病指出,邪在少阳,往来寒热,必用柴胡。因予小柴胡汤原方,其中柴胡每剂用24克。共服3剂,低热全退,患者自觉全身舒适。由此看出人工智能中医学数学模型得出的计算结果与老中医专家开出的中药方是一致的。

综上所述,深度学习中医学的数学模型是将原数学模型变换了一种形式,使模型简单化,数学表述图像化,逻辑关系清晰化。此模型的优点是:清晰明确的逻辑关系,用数学公式表示的方法简单方便;用分支分层的方法,把各个分支和各层数据一一列出并进行计算,条理清楚,定性准确,定量分析的结果符合实际要求;成本低、效率高、可操作性强并且计算量低。

4 结论

将中医学理论用数学模型和抽象化数学公式来表示,简单明了。简单的数学公式便于分析和计算中医学数学模型的各种数据。中医学数学模型可以变成动态的数据图,从而反映数据的实时运行情况，解决各种条件下数据各单位的排序问题。其具有加密数据的特点,还可以优化数据并满足数据拓扑管理的要求,从而便于数据的分级管理。形成了系统、全面的人工智能中医学数学模型分析体系。中医理论的数学模型可以在计算机上训练中医师，并对某些疑难杂症进行人工智能研究,再进行临床试验研究。通过把所有古代与现代中医临床经验输入这个平台,并不断更新病例进行总结和学习。

中医学数学模型的应用需要大量的数据与计算分析结果,需要大量人力物力的投入。目前处于初步探索阶段,已经有数学家在中医的数学化方面进行研究,一些中医医疗平台也开始做这方面的工作,但利用人工智能中医学治疗疾病还没有开展。在不久的将来,中医学一定会走向数学化人工智能化,走出中国,走向世界,造福人类。