基于EMPC 方法的旋转倒立摆控制*
2020-12-28马永凌
马永凌
(武夷学院机电工程学院,福建武夷山 354300)
0 引言
旋转倒立摆是一个结构不复杂、成本不高、体积不大的实验设备,但却是一个非线性、强耦合、多变量的自然不稳定被控制对象,被广泛应用于控制理论的研究,是个理想的研究平台。模型预测控制(MPC)技术是一种处理多变量约束系统最优控制问题的最有效方法之一。但由于模型预测控制需要实时的在线优化,因此只能应用于慢速过程,不适用于旋转倒立摆系统。为此本文研究显式模型预测控制(EMPC)控制器,将在线的优化求解计算放到离线进行,从而提高在线计算的速度,完成对旋转倒立摆的平衡点控制,并用Matlab进行仿真。
1 旋转倒立摆系统数学模型的建立
如图1所示为旋转倒立摆的模型结构,摆杆由于重力作用,在垂直方向上会自然地摆到垂直向下的位置,为自然不稳定的被控制对象。本研究的控制目的为通过电机使旋臂转动,并且通过旋臂的转动带动摆杆,使摆杆能够保持在垂直向上的不稳定的平衡点位置上。
在不考虑各种摩擦力与阻力的前提下,可以把摆杆与旋臂都抽象为匀质杆,其中摆杆的长度为L,相对于其垂直向上的方向零位的角位移为θ;旋臂的长度为R,相对于其水平方向上的方向零度的角位移为α。
对于此旋转倒立摆本研究采用拉格朗日方程进行数学建模如下式:

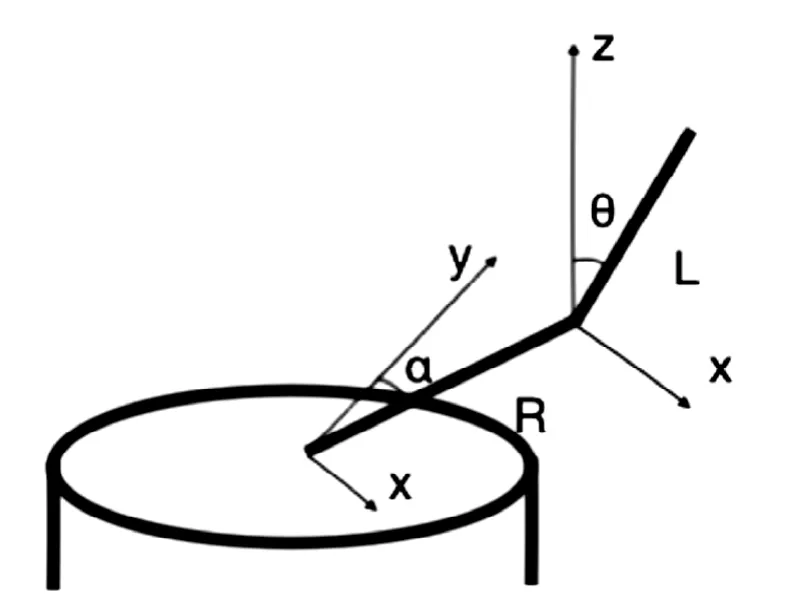
图1 旋转倒立摆结构
通过其次坐标变换[1]推得系统包括平动动能和转动动能的总动能与势能如下式:

其中H为拉格朗日算子; qi为系统的广义坐标;fi为系统的广义力;T为系统的动能;V为系统的势能。
在系统中,i=1,2,q={α,θ},可得方程组[2]:

其中To为直流伺服电机的输出转矩如下式(7)所示:

上述各参数的物理意义如表1所示。
若以Vm直流电机电枢电压作为输入,摆杆角位移θ为输出,且在平衡点(αθ)T=(0000)T附近可局部线性化,则可推出此旋转倒立摆系统如下式的线性化状态方程:

旋转倒立摆的模型总是具有一定的非线性和时变性,模型的结构与参数总是具有一定的摄动特性,以及模型总是存在一些外部的干扰,本研究的控制方案就是在此线性化后的状态空间模型上进行的。
2 显式模型预测控制
MPC为Model Predictive Control的缩写,又称模型预测控制。MPC模型预测控制的基本运行机理为:(1)预测系统未来动态求解。(2)优化路径问题。(3)解得的第一个元素直接作用于系统。(4)滚动时域、重复进行。
在MPC模型预测控制中存在反复在线优化的模块,使得模型预测控制普遍只适用于慢速过程,很难以适用于动态变化较快的旋转倒立摆控制。然而Bemporad等人在2002年提出来的EMPC是一种面向小规模控制命题的快速MPC算法[3-5]。
EMPC为Explicit Model Predictive Control的缩写,又称显式模型预测控制。EMPC显式模型预测控制的主要思想是通过多参数二次规划的思想,将在线的优化求解计算放到离线进行,从而提高在线计算的速度,使得显式模型预测控制能够适用于动态变化较快的旋转倒立摆控制。

表1 系统物理参数意义表
建立一个离散的,线性时不变的状态空间模型:

此多参数二次规划问题可以表述为:
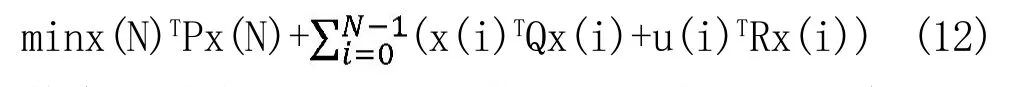

关于多参数二次规划问题,式(13)优化命题的KKT条件为(上标星号的是最优值):

求解式(14)得到(下标a的表示有效的约束,下标i的表示无效的约束):
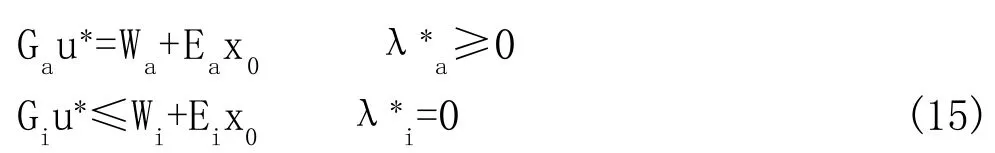
按照EMPC的理论,由上面的KKT条件得到以下的方程组:
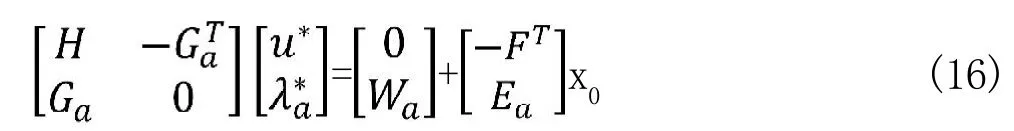
假设Ga矩阵行满秩,上述方程组可解,得到与状态参数x0线性相关的解:
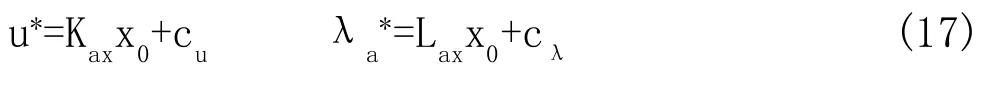
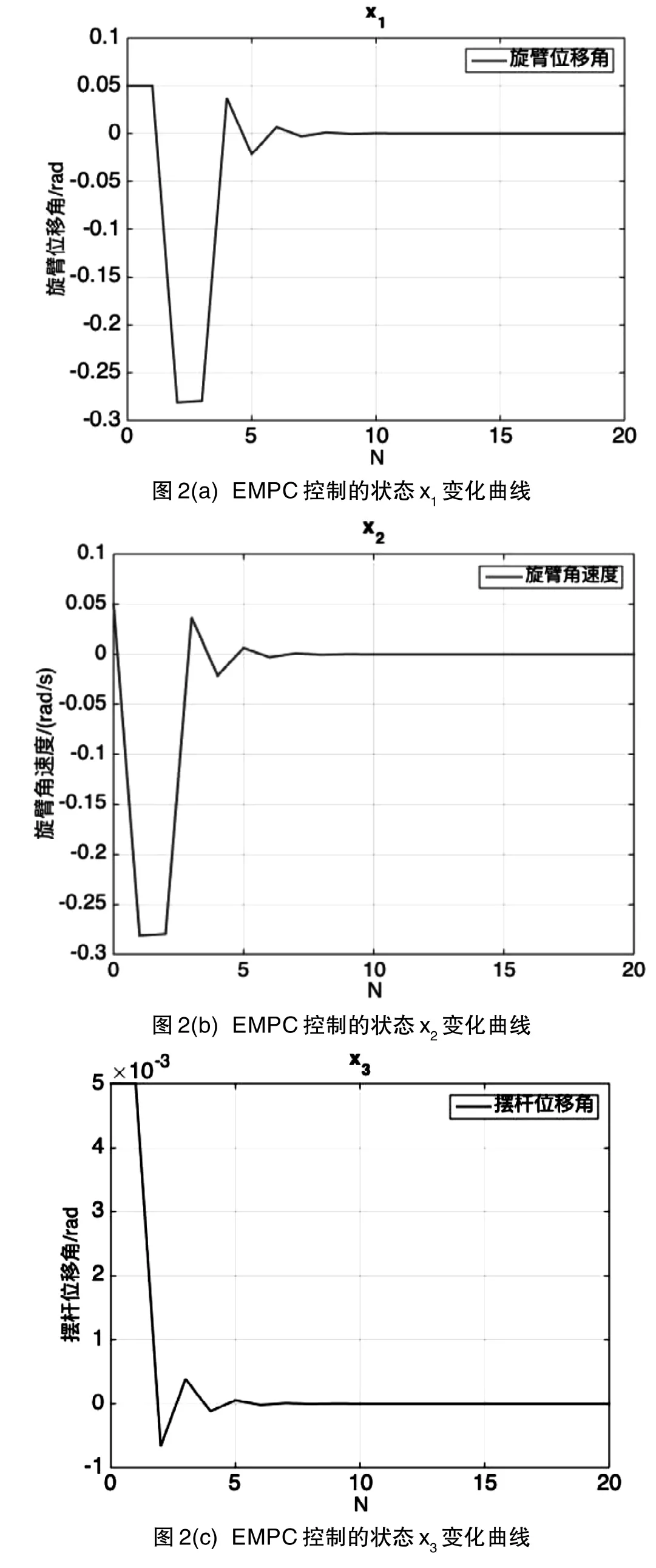
其中:
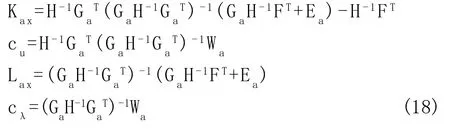
其中Kax,cu,Lax,cλ都和参数x0并没有关系。而这些参数所适用的可行区域,也就是EM PC 中所谓的关键区域(CR)。这些区域是由KKT条件中剩下的几个不等式来确定的,如果用式(18)的解替换掉KKT条件中不等式的变量,就可以得到:

因为上面的不等式都是关于当前时刻状态x0的线性不等式,因此可以将整个状态空间内划分出很多个互不重叠的CR。由此可以得到与隐式闭环模型预测控制系统等价的显式模型预测控制系统,即分段防射(PWA)系统。

3 EMPC下旋转倒立摆系统仿真
为了评估EMPC显示模型预测控制方法的控制性能,本文引入显式模型预测控制技术通过利用Matlab对旋转倒立摆进行计算机仿真研究。
其中有3个工具箱可以使用进行仿真:(1)MPT3为Multi-Parametric Toolbox 3的缩写,又称多参数工具箱,是一个开源的,基于Matlab的工具箱,用于参数优化,计算几何模型和模型预测控制。(2)Hybrid Toolbox,是由EMPC显式模型预测控制的提出者Alberto Bemporad创作的工具箱。这工具箱可以针对线性系统直接设计模型预测控制(MPC)以及显式模型预测控制(EMPC)控制器,对于混合系统(Hybrid system)同样十分适用。(3)Matlab中也有自带的函数,其调用也十分方便。
以上三种方式都能有效地实现EMP C显式模型预测控制,相互之间又各有差异与侧重点,大家可以依据需求选择自己的方法。
由于调用MPT3的方式十分简洁,几行代码就能输出显式MPC控制器,并且能够直接绘图,更加直观。因此本文通过利用Matlab的MPT3工具箱对旋转倒立摆进行计算机仿真研究。
对于旋转倒立摆,引入状态变量为:

X的约束条件为:

引入输入控制变量U=Vm,其中Vm为直流电机电枢电压,其约束条件为:

设初始状态为:
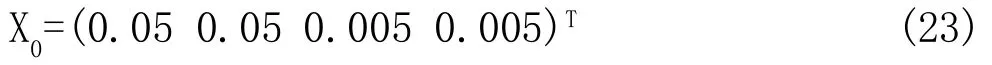
得到旋转倒立摆系统的EMPC控制结果如图2所示。
从图2中可以得知,通过显式模型预测控制,旋转倒立摆的旋臂与摆杆能够在短时间间内精确地稳定在平衡点附近,并且各状态变量也都能够控制在之前设定的约束条件之内,仿真符合预期。
通过仿真研究能够发现:(1)显式模型预测控制的耗时更少;(2)显式模型预测控制精确性更高;(3)显式模型预测控制对于有约束系统的控制更有效,并且不难发现通过显式模型预测控制能够把状态变量与输入变量的变化控制在预设的约束范围之内。
但是EMPC显式模型预测控制也有他的局限性,实际应用过程中EMPC显式模型预测控制还是有它自身的限制的,最大的短处就是求得的控制率函数比较复杂,而且函数的复杂度随着参数的增多(比如预测步长Np的增大)呈指数增长,这样仿真计算的时间会越来越长,系统所需要的存储空间会越来越大,所以一般EMPC也仅适用于小规模的问题,如旋转倒立摆系统。如果要缩小EMPC显式模型预测控制的运算时间或者系统储存空间,就不得不要放弃一部分的准确度。
4 结语
本文首先基于拉格朗日方程对旋转倒立摆在不稳定平衡点上摆进行了线性化的数学建模。然后对于EMPC显式模型预测控制的控制原理进行了分析推理。通过EMPC显式模型预测控制的控制使摆杆能够保持在垂直向上的不稳定的平衡点位置上,从仿真结果来看效果不错。显式模型预测控制(EMPC)作为模型预测控制(MPC)的一个重要分支,从被提出至今已经有将近20年的历史了。简单来说,显式模型预测控制就是在传统的模型预测控制基础上,将原本需要在线(on-line)优化求解的控制量转化成离线(off-line)模式。换句话说,将控制量表示为一个关于状态量x_0的函数,而且这函数是piecewise-affine(PWA分段仿射)函数。但关于EMPC显式模型预测控制方法改进的研究还是一件任重而道远的事。要在系统存储量要求高、运算耗时量大与控制精确度中作出取舍,使之达到最优的控制效果。
