“非有理真分式”情况下拉普拉斯逆变换方法探究*
2020-12-28曹丽娟陈中政张黎红
曹丽娟 陈中政 张黎红
(东莞理工学院城市学院,广东东莞 523419)
0 引言
信号与系统是大学本科理工科专业的一门重要技术基础理论课程,在各个高校的电子信息科学与技术、电子信息工程、自动控制、机电一体化、电气工程及其自动化等专业中,该课程的应用较为广泛,每年有数以万计的学生学习该门课程。此课程主要讲解傅里叶变换、拉普拉斯变换和Z变换这三大经典变换的相关知识,其中,拉普拉斯变换对分析系统稳定性起着非常重要的作用。笔者针对非有理真分式情况下,求解拉普拉斯逆变换的方法,查阅国内外经典教材和文献,发现基本都是提出先利用多项式长除法,将非有理真分式化成有理真分式后,再进行部分分式展开法求解。而利用多项式长除法将非有理真分式化成有理真分式的计算量不小,因此这种传统的方法解题显得比较繁琐。本文介绍的方法可省略“多项式长除法将非有理式真分式化成有理真分式”的环节,直接进行部分分式展开法求解逆变换,该方法快捷有效,具有一定的推广价值。
1 问题提出
1.1 传统解法
吴大正[1]主编的“信号与线性系统分析(第四版)”的232页,和郑君里[2]主编的“信号与系统(第三版)”上册的203页中,都有这样的描述:如果象函数F(s)是s的实系数有理分式,可写为:
若m≥n(非有理真分式),可用多项式长除法将象函数F(s)分解为有理多项式P(s)与有理真分式之和,即F(s)
其中,吴大正主编的“信号与线性系统分析(第四版)”的232页中,还举了一个例子:
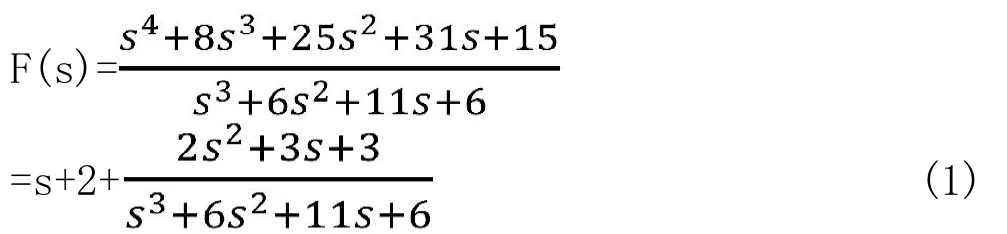
同时,教材也以n≥m(有理真分式)为例,详细讲解了如何根据极点的不同情况,利用部分分式展开法,来求解其拉普拉斯逆变换的过程。
接下来笔者将以上面所列的教材中的非有理真分式“式1”为例,根据教材给出的传统方法进行求解:


显然,可以看出属于单一极点情况,故可利用部分分式展开法变形为:

其中,常数K1、K2、K3分别为:

最后利用常见拉普拉斯变换对公式,即可求出象函数F(s)对应的原函数f(t)的表达式。
以上是非有理真分式情况下,传统方法的分析过程,即:先利用多项式长除法将非有理真分式化成有理真分式,然后再进行部分分式展开法求解。
1.2 本文解法
接下来用本文推荐的方法同样求解该题,分析过程如下[3-4]:
非有理真分式“式1”中的:

注意,这里根本不涉及“传统的长除法”,也更不需要利用“传统的长除法”去得到B(s)是具体的多少,所以,此处便可以节约长除法计算B(s)的大量时间,避免“因计算量大,而造成的出错概率上升”的问题。
当然,为看出其极点分布情况,可将上式5变形为下式(6):
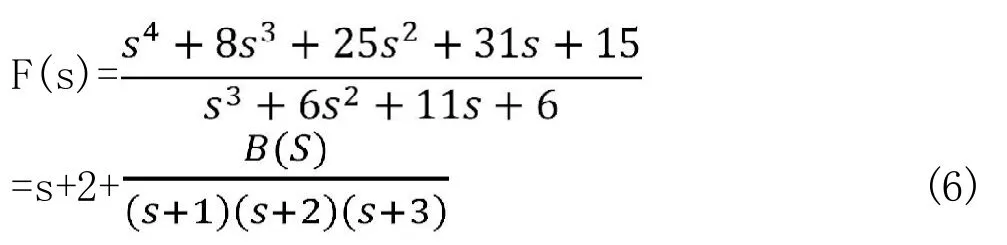
显然,可以看出属于单一极点情况,故可利用部分分式展开法变形为:
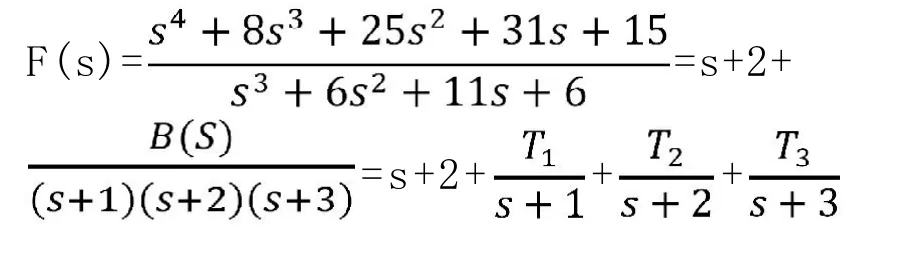
其中,这里的待定系数T1、T2、T3,可用下面公式求出:
最终也可得到:
显然,与传统方法得到结果相同。但是,对比两种方法,可以明显发现,区别主要表现在两个地方:(1)将非有理真分式“式1”变成“式5”,不用利用长除法去运算,仅通过比较“分母中高于分子的s最高次项”的次数和系数即可,从而降低因长除法计算量大造成的出错可能。(2)同样用“待定系数法”求解时,“式4”中求K1、K2、K3,依赖于“式2”的长除法结果;而在“式7”中用待定系数法求T1、T2、T3,直接代入的是已知的F(s),完全避开了“长除法”。
2 原理证明
本文所提出的方法和传统教材上介绍的方法的本质区别在于:本文所提出的新方法可省掉“利用多项式长除法将非有理真分式化成有理真分式”的环节,直接利用部分分式展开法。该方法能成立的原理证明如下:
因为,当m≥n(非有理真分式),用多项式长除法将象函数F(s)分解为有理多项式P(s)与有理真分式之和,即
当用“待定系数法”求解时,无论“式4”中求K1、K2、K3,还是“式7”中用待定系数法求T1、T2、T3,代入的值都是极点,即令A(s)=0的s值。
3 总结
本文通过分析“非有理真分式情况下,求解拉普拉斯逆变换的方法”,查阅国内外经典教材及文献,发现基本都是提出先利用多项式长除法,将非有理真分式化成有理真分式后,再进行部分分式展开法求解。而利用多项式长除法将非有理真分式化成有理真分式的计算量不小,考虑到该传统方法解题比较繁琐,本文提出一种的新方法可省略“多项式长除法将非有理式真分化成有理真分式”的环节,直接进行部分分式展开法求解逆变换,事实证明该新方法快捷有效,具有很好的推广价值。特别说明,本文对比新旧两种方法时,选用的是教材中的实例,极点属于单根情况,对于“共轭复根、重根”的情形也适用,本文不在罗列,有兴趣者,可自行验证,本质原理都是一样的。
