社会比较情境下情感演化机理分析

谢能刚，代亚运，暴 伟，王 萌

(安徽工业大学a.管理科学与工程学院；b.商学院，安徽马鞍山243032)

人类之间的交流与互动是富有情感的，在不同情感驱动下，人们会做出相应的行为选择并获得不同的得益。Bu等[1]对中文网络论坛中用户交流评论的语义取向和潜在情感进行定量评价，并基于博弈论对用户的情感演化动态进行分析预测。Tooby等[2]认为情感特质之所以拥有适应性优势，是因为情感影响个体的成本及收益权衡，并帮助个体优化决策。Leith等[3]发现,当被试者体验到“尴尬”或“愤怒”时会采取高风险高回报策略，当体验到幸福或悲伤时则力图避免采取这种策略。

人类的情感丰富多样，如喜怒哀乐、羡慕嫉妒恨等，多元的情感由不同的情境引发，所谓心由境生、情由境迁，其中一些情感，如同情、欺凌、尊敬、嫉妒等，是基于相应的社会比较情境产生的。社会比较是一种普遍存在的大众心理现象，其对个体行为决策起发动和定向作用，使行动活性化和稳定化。Wills[4]关于社会比较对情绪引发的研究表明，个体在与强者比较中易出现负性情绪，在与弱者比较中易产生积极情绪；Gerber等[5]通过分析比较目标的选择和比较对自我评价、情感等的影响表明，当自身利益不受到威胁时，个体倾向于选择强者进行比较；Fehr等[6]认为个体与他人比较时会产生内疚(高于对方时)和嫉妒(低于对方时)情绪，并引发相应的合作和竞争行为；Wood[7]、Aspinwall等[8]通过研究社会比较对自我满足感的影响发现，与弱于自己的人比较将提高自尊，与强于自己的人比较将降低自尊；倪青青[9]基于心理理论的调节作用，分析社会比较对儿童公平分配行为的影响，研究结果显示心理情感、社会比较与儿童公平分配行为存在显著相关关系；李妍[10]通过研究社会比较对个体亲社会行为的影响发现，他人等级地位和他人决策结果影响个体本身亲社会行为的决策。

社会比较的过程和信息会影响个体的社会行为，个体在社会比较中引发的情感和相应的行为决策具体为个体之间的冲突、竞争与合作，主要目标为通过个体之间的相互博弈实现自身利益的最大化。Szolnoki等[11-12]给个体赋予两个情感参数，建立情感特征与合作策略之间的定量映射关系，认为网络邻居之间的情感模仿可提高群体适应度，嫉妒是抑制个体合作的重要因素。Wang等[13]和Ye等[14]基于最后通牒博弈模型，通过定义付出水平和净收益接收水平2个参数，将情感类型分为慷慨、吝啬、善良、贪婪4种类型，建立情感特征与博弈得益之间的定量映射关系，演化博弈结果显示：具有公平性和适度善良性的个体适者生存；公平的方案并不能保证群体高收益，对净收益持适度负预期的善良是群体合作并取得高收益的原因。Xie等[15]将情感类型分为4种，即对强者的尊敬与嫉妒和对弱者的同情与欺凌，采用遗传算法对种群的演化行为进行仿真研究，结果显示，情感的多样性能有效促进合作的产生，其中同情和尊敬的情感更具进化优势。以上的演化博弈动力学分析均是基于数值仿真方法(如Monte Carlo计算仿真)，缺少针对情感演化动态的理论分析。基于此，文中建立个体情感与竞合行为之间的映射关系，利用复制动态方程研究社会比较情境下情感的演化机制，分析其平衡点及稳定性，获得情感系统达到演化稳定策略(ESS)时的条件和演化路径。

1 情感博弈模型

1.1 个体情感与竞合行为之间的对应关系

假设面对“弱者”(对手在能力、资源和禀赋等方面弱于自己)时，个体会产生2 种类型的情感：同情和欺凌。面对“强者”(对手在能力、资源和禀赋等方面强于自己)时，个体会产生另外2 种类型的情感：尊敬和嫉妒。同时，设定个体的行为策略为合作和竞争2种方式，个体的4种情感类型与2种行为策略之间的定性对应关系为同情和尊重对应合作行为、欺凌和嫉妒对应竞争行为。

1.2 博弈模型

表1为强者和弱者2个博弈方的情感和对应行为下的收益矩阵(弱者收益在前)。其中R为双方合作的奖励，一般取值为1；P为相互竞争的惩罚，一般取值为0；T为竞争成功的诱惑，取值为0≤T≤2；S为合作失败的代价，取值为-1≤S≤1。根据博弈模型的定义[11]：参数关系满足T＞R＞P＞S 时，为囚徒困境博弈模型(PD博弈)；参数关系满足T＞R＞S＞P时，为雪堆博弈模型(SD 博弈)；参数关系满足R＞T＞P＞S时，为猎鹿博弈模型(SH博弈)；参数关系满足R＞T＞S＞P 时，为和谐博弈模型(HG 博弈)。可以看出，在和谐博弈模型中，合作永远是赢家战略。基于参数T和S变化的4种博弈模型取值区域如图1。

表1 博弈得益矩阵Tab.1 Game benefit matrix

图1 4种博弈模型Fig.1 Four game models

1.3 复制动态方程

目前宏观水平上使用最多的演化博弈分析模型是由Taylor 等[16]提出的复制者动力学方程，其理性假设为种群中某既定策略密度的单位增长α̇/α 正比于该策略适应度与种群平均适应度之差。文中针对强者和弱者的情感演化，建立复制动态方程。设强者产生同情情感的概率为x，弱者产生尊敬情感的概率为y。

强者同情弱者的期望收益Es1为

强者欺凌弱者的期望收益Es2为

强者以x的概率选择同情,以1-x 的概率选择欺凌混合策略的期望收益Es为

弱者尊敬强者的期望收益Ew1为

弱者嫉妒强者的期望收益Ew2为

弱者以y的概率选择尊敬,以1−y的概率选择嫉妒混合策略的期望收益Ew为

系统复制动态方程为

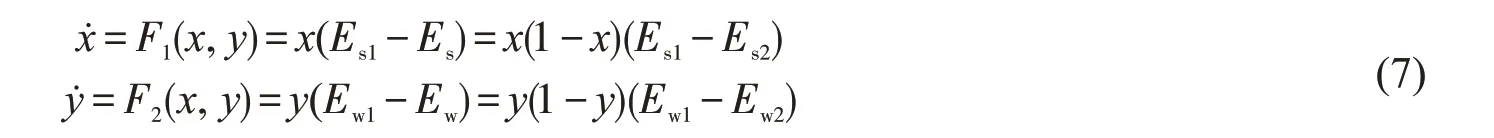
利用式(1)，(2)，(4)，(5)，并将R=1，P=0 代入可得：

2 复制动态方程理论分析

2.1 平衡点计算

1)无论支付变量T，S 取何值,式(8)均有4组确定解(0,0)，(0,1)，(1,0)，(1,1)；

2)当S ＞0 且T+S ＞1或者S ＜0 且T+S ＜1，式(8)另有一组解(S/(T+S-1)，(S/(T+S-1))；

3)特殊条件下，S=0 时有无数组特殊解(∼,0)或(0,∼)，T=1时有无数组特殊解(∼,1)或(1,∼)。

2.2 稳定性分析

利用复制动态方程的相位图和稳定性定理等分析演化稳定策略(evolutionary stabilization strategy，ESS)，文中针对2.1节求得的平衡点进行稳定性分析，其中的稳定点就是ESS，从而找到达到ESS 的条件和演化机理。

针对形如式(8)的非线性方程，主要采用近似线性方法判断其平衡点的稳定性。在平衡点处将非线性方程作Taylor展开，取一次项得近似线性方程；获取线性方程的系数矩阵(Jacobi矩阵)；计算Jacobi矩阵的秩detJ 和迹trJ，通过表2 判断平衡点的稳定性[17]。经计算推导，式(8)对应的Jacobi矩阵为

表2 平衡点类型判别Tab.2 Judgment of balance point type

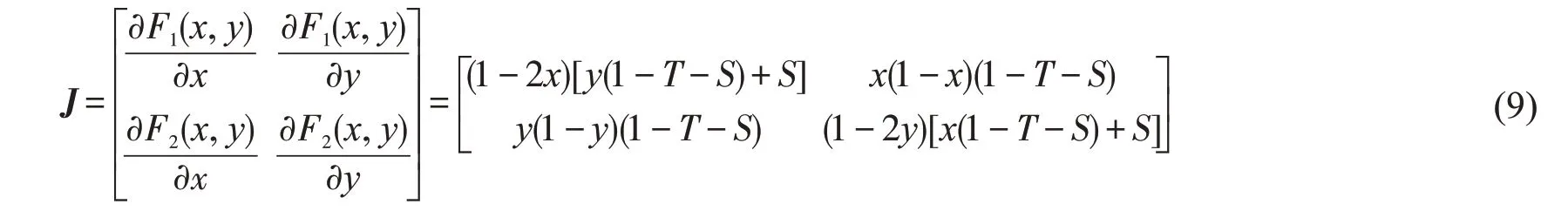
将2.1节得到的平衡点代入式(9)，分别计算对应的Jacobi矩阵的秩和迹，结果如表3。

表3 系统平衡点对应的Jacobi矩阵的秩和迹Tab.3 Rank and trace of the Jacobi matrix corresponding to the system equilibrium point

2.2.11 ＜T ≤2且0 ＜S ≤1

表4为1 ＜T ≤2 且0 ＜S ≤1 情形(对应图1中的SD博弈模型)系统的平衡点类型判断。分析表4可看出：弱者面对强者时，若强者同情弱者，则弱者嫉妒强者比尊敬强者得到的收益大，所以弱者会嫉妒强者；若强者欺凌弱者，则弱者尊敬强者比嫉妒强者得到的收益大，所以弱者会尊敬强者。强者面对弱者时，如果弱者尊敬强者，那么强者欺凌弱者比同情弱者得到的收益大，所以强者会欺凌弱者；如果弱者嫉妒强者，那么强者同情弱者比欺凌弱者得到的收益大，所以强者会同情弱者。(0,1)和(1,0)为系统演化的稳定点。其中：(0,1)对应强者完全(100%)欺凌弱者和弱者完全尊敬强者；(1,0)对应强者完全同情弱者和弱者完全嫉妒强者。

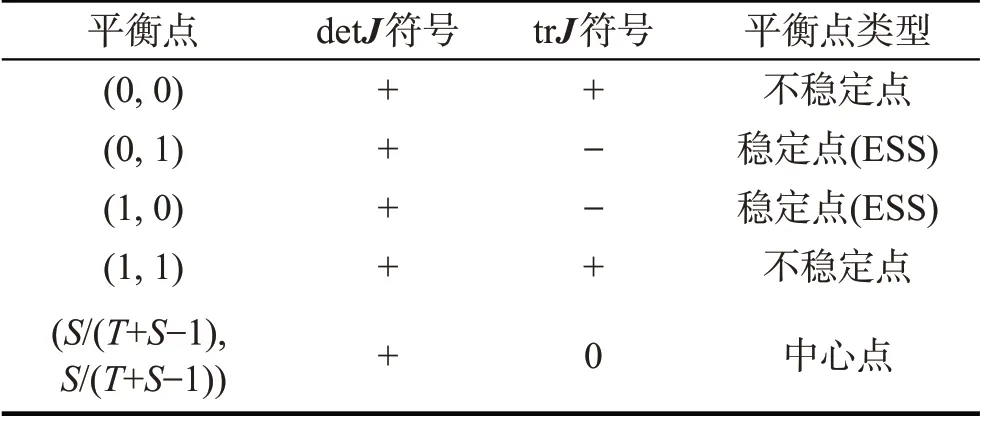
表4 系统平衡点类型判断(1＜T≤2且0＜S≤1)Tab.4 Judgment of system balance point type(1＜T≤2 and 0＜S≤1)

T=1.5 和S=0.5 时，不同初始值下的情感演化路径如图2。由图2可看出：y ＞x 时，即弱者产生尊敬情感的概率大于强者产生同情情感的概率时，博弈系统会收敛于稳定点(0，1)，对应强者完全欺凌弱者和弱者完全尊敬强者；y ＜x 时，即弱者产生尊敬情感的概率小于强者产生同情情感的概率时，博弈系统会收敛于稳定点(1，0)，对应强者完全同情弱者和弱者完全嫉妒强者；y=x时，即弱者产生尊敬情感的概率等于强者产生同情情感的概率时，系统收敛于中心点(0.5，0.5)，对应收敛结果为强者等概率同情和欺凌弱者，弱者等概率尊敬和嫉妒强者。

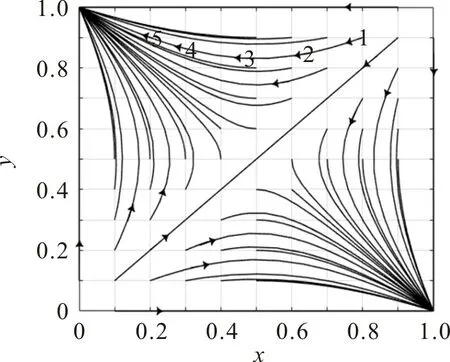
图2 T=1.5且S=0.5时x-y的演化路径Fig.2 Evolution path of x-y with T=1.5 and S=0.5

以(x，y)初始值取(0.8，0.9)的演化路径为代表分析图2，如图中有数字标号的一条演化路径。将T=1.5，S=0.5 及R=1，P=0 代入式(3)，(6)可得，强者的平均期望收益Es=1.5y+0.5x-xy，弱者的平均期望收益Ew=1.5x+0.5y-xy，强者对弱者的相对收益Es-Ew=y-x。在1 号位置(初始点)，强者的同情概率x 为0.8，弱者的尊敬概率y 为0.9，此时强者的收益为1.03，弱者的收益为0.93，强者和弱者的收益均较高。但强者对弱者的相对收益为正(0.1)，弱者为减少与强者之间的收益差距，会首先降低y，随着y的减小，强者为保持对弱者的相对收益为正，会随之降低x，这就有图中位置1→2→3的演化。3号位置的(x,y)约(0.50,0.85)，强者的收益为1.10，弱者的收益为0.75，可以发现，从1→2→3的演化不仅没有缩减弱者和强者间的收益差距，反而弱者的收益相对初始位置还有所降低。因此，当x 从0.5继续减小时，弱者的平均期望收益Ew=1.5x+0.5y-xy=1.5x+(0.5-x)y，弱者为弥补由x减小带来的收益降低趋势，会提升y，这就产生了由3→4→5并收敛于(0,1)的演化路径。

2.2.21 ＜T ≤2且-1 ≤S ＜0

表5 为1 ＜T ≤2 且-1 ≤S ＜0 情形(对应图1 中的PD 博弈模型)系统的平衡点类型判断。分析表5 可看出：对于弱者，无论强者是同情还是欺凌，弱者嫉妒强者得到的收益会大于尊敬强者得到的收益，所以弱者会嫉妒强者；对于强者，无论弱者是尊敬还是嫉妒，强者欺凌弱者得到的收益会大于同情弱者得到的收益，所以强者会欺凌弱者。演化结果显示：(0,0)为稳定点，(1,0)，(0,1)为鞍点，(1,1)为不稳定点；(0,0)对应强者完全欺凌弱者和弱者完全嫉妒强者的情形。

虽然我国大多数自然村村级财务管理工作采取了定期公开的制度，但是由于其公开的内容缺乏实质性，很多在内容上都属于空洞，因此不够具体。广大群众无法了解资金实际使用的用途，不能够有效资金进行民主的监督。同时整个资金管理意识较为缺乏，资金管理较为淡薄，特别是由于我国农村分散式的居住环境也导致了对村级财务管理工作的监督效果大打折扣。一些村民对于村集体的财务管理工作不够关心，缺乏相应的责任心，给了一些干部腐败以可乘之机，因此财务管理工作漏洞百出，很容易导致村级财务管理工作的腐败现象。

表5 系统平衡点类型判断(1＜T≤2且-1≤S＜0)Tab.5 Judgment of system balance point type(1＜T≤2 and-1≤S＜0)

T=1.5 和S= -0.5 时不同初始值下的情感演化路径如图3。由图3 可看出：对于除x=1 或y=1外的x，y 初始值，博弈系统都会收敛于稳定点(0,0)；当x=1 或y=1 时，系统会分别收敛于鞍点(1,0)和(0,1)。

图3 T=1.5且S=-0.5时x-y的演化路径Fig.3 Evolution path of x-y with T=1.5 and S=-0.5

2.2.30 ≤T ＜1且0 ＜S ≤1

表6 为0 ≤T ＜1 且0 ＜S ≤1 情形(对应图1 中的SH博弈模型)系统的平衡点类型判断。分析表6可看出：对于弱者，无论强者是同情还是欺凌，弱者尊敬强者得到的收益会大于嫉妒强者得到的收益，所以弱者会尊敬强者；对于强者，无论弱者是尊敬还是嫉妒，强者同情弱者得到的收益会大于欺凌弱者得到的收益，所以强者会同情弱者。演化结果：(1,1)为稳定点，(1,0)，(0,1)为鞍点，(0,0)为不稳定点；(1,1)对应强者完全同情弱者和弱者完全尊敬强者的情形。

表6 系统平衡点类型判断(0≤T＜1且0＜S≤1)Tab.6 Judgment of system balance point type(0≤T＜1 and 0＜S≤1)

取T=0.5 和S=0.5，作不同初始值下的情感演化路径，如图4。由图4可看出：对于除x=0 或y=0外的x，y初始值，博弈系统都会收敛于稳定点(1,1)；当x=0 或y=0 时，系统分别收敛于鞍点(0, 1)和(1,0)。

图4 T=0.5且S=0.5时x-y的演化路径Fig.4 Evolution path of x-y with T=0.5 and S=0.5

2.2.4 0≤T＜1且-1≤S＜0

表7 为0 ≤T ＜1 且-1 ≤S ＜0 情形(对应图1 中的HG博弈模型)系统的平衡点类型判断。分析表7可看出：弱者面对强者时，如果强者同情弱者，那么弱者尊敬强者比嫉妒强者得到的收益大，所以弱者会尊敬强者；如果强者欺凌弱者，那么弱者嫉妒强者比尊敬强者得到的收益大，所以弱者会嫉妒强者。强者面对弱者时，如果弱者尊敬强者，那么强者同情弱者比欺凌弱者得到的收益大，所以强者会同情弱者；如果弱者嫉妒强者，那么强者欺凌弱者比同情强者得到的收益大，所以强者会欺凌弱者。演化结果显示(0,0)和(1,1)为稳定点，分别对应“妒强凌弱”和“敬上爱下”的系统状态，表明强者和弱者之间的针锋相对是演化稳定策略。

表7 系统平衡点类型判断(0≤T＜1且-1≤S＜0)Tab.7 Judgment of system balance point type(0≤T＜1 and-1≤S＜0)

T=0.5 和S=-0.5 时，不同初始值下的情感演化路径如图5。

由图5可看出：(x+y)＜1 时，即强者产生同情情感的概率与弱者产生尊敬情感的概率之和小于1时，博弈系统收敛于稳定点(0,0)，也就是当系统的初始良性情感不占优势时((x+y)＜1)，系统会最终演化到“妒强凌弱”的恶性状态；(x+y)＞1 时，即强者产生同情情感的概率与弱者产生尊敬情感的概率之和大于1时，博弈系统收敛于稳定点(1,1)，也就是当系统的初始良性情感占优势时((x+y)＞1)，系统会最终演化到“敬上爱下”的良性状态；(x+y)=1 时，系统收敛于中心点为(0.5,0.5)，收敛结果为强者等概率同情和欺凌弱者，弱者等概率尊敬和嫉妒强者。

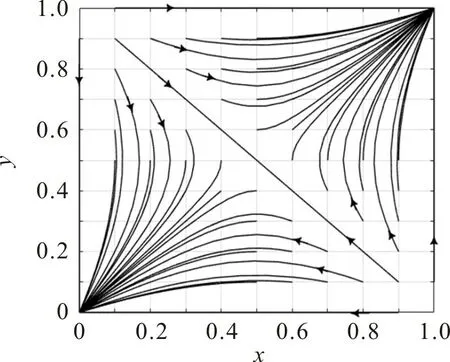
图5 T=0.5且S=-0.5时x-y的演化路径Fig.5 Evolution path of x-y with T=0.5 and S=-0.5

2.2.5T=1和S=0

上述分析中未包括T=1 和S=0 的情形，表8为T=1 和S=0 的参数取值情况下系统平衡点的稳定性分析结果。

表8 系统平衡点类型判断(T=1和S=0)Tab.8 Judgment of system balance point type(T=1 and S=0)

2.2.6 1＜T≤2且0＜S≤1和0≤T＜1且-1≤S＜0

1)1＜T≤2 且0＜S≤1 时，演化结果显示：(0,1)和(1, 0)为稳定点，(S/(T+S-1)，S/(T+S-1))为中心点。令(x0,y0)为中心点(S/(T+S-1),S/(T+S-1))，分别取S=0.2，T=1.6 和S=0.6，T=1.2 两组数据绘演化趋势，结果如图6。

由图6 可看出，T 和S 取值变化时，中心点位置随之改变，同时由区域1 和2(演化至稳定点(0,1))、区域3 和4(演化至稳定点(1,0))构成的两个演化收敛域形状也随之改变。但是，两个演化收敛域的面积大小和T，S 的取值无关，两个收敛域面积均占总面积的50%。系统演化到稳定点(0,1)或(1,0)取决于(x,y)的初始取值，即系统初始状态决定了系统最终的演化稳定状态。

图6 1＜T≤2且0＜S≤1时的系统演化趋势Fig.6 System evolution trend at 1＜T≤2 and 0＜S≤1

2)0≤T＜1 且-1≤S＜0 时，演化结果显示：(0,0)和(1,1)为稳定点，(x0,y0)为中心点(S/(T+S-1)，S/(T+S-1))。S=-0.2，T=0.4和S=-0.6，T=0.8时，系统演化趋势如图7。

图7 0≤T＜1且-1≤S＜0时的系统演化趋势Fig.7 System evolution trend at 0≤T＜1 and-1≤S＜0

从图7 可看出，T 和S 取值变化时，中心点位置随之改变，同时由区域1 和4(演化至稳定点(1,1))、区域2 和3(演化至稳定点(0,0))构成的两个演化收敛域形状和面积大小也在改变。令P00表示收敛于稳定点(0, 0)的收敛域面积占总面积的比例，P00与T，S取值关系如图8。

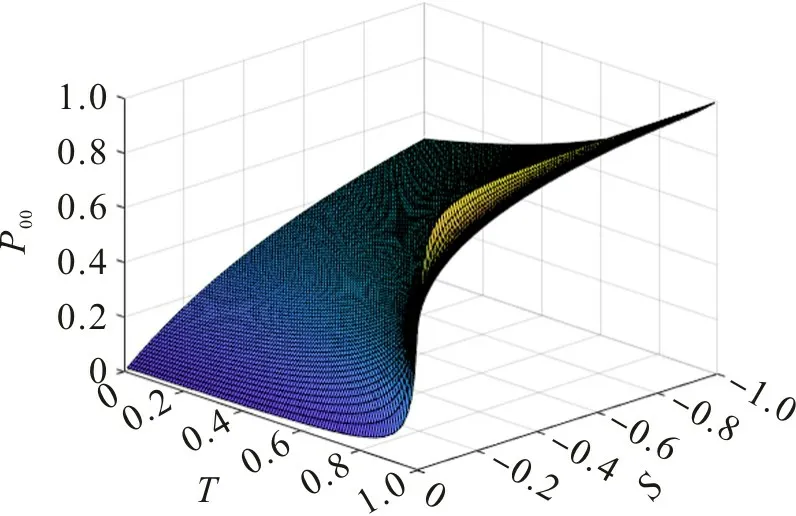
图8 P00与T，S的关系Fig.8 Relationship between P00 and T,S

3 噪声的影响分析

由于“颤抖的手”导致的失误，使得情感驱动的行为决策出现偏差，假设情感以1-c 的概率对应原行为，以c 的概率对应相反行为。若强者的情感为同情，则和弱者合作的概率为1-c，和弱者竞争的概率为c。c 为系统噪声。

在4种情感均考虑系统噪声c 的情形下，强者平均期望收益为

式中：Ecs1=(1-c){[(1-c)y+c(1-y)]+[cy+(1-c)(1-y)]S}+c[(1-c)y+c(1-y)]T，为系统噪声环境下强者同情弱者的期望收益；Ecs2=c{[(1-c)y+c(1-y)]+[cy+(1-c)(1-y)]S}+(1-c)[(1-c)y+c(1-y)]T，为系统噪声环境下强者欺凌弱者的期望收益。

对于4种情感均考虑系统噪声c 的情形下，弱者平均期望收益为

式中：Ecw1=(1-c){[(1-c)x+c(1-x)]+[cx+(1-c)(1-x)]S}+c[(1-c)x+c(1-x)]T，为系统噪声环境下弱者尊敬强者的期望收益；Ecw2=c{[(1-c)x+c(1-x)]+[(cx+(1-c)(1-x)]S}+(1-c)[(1-c)x+c(1-x)]T，为系统噪声环境下弱者嫉妒强者的期望收益。

对于4种情感均考虑系统噪声c的情形下，系统复制动态方程为：

基于囚徒困境博弈模型(PD 博弈模型)，即1＜T≤2且-1≤S＜0下，对式(12)进行平衡点计算和稳定性分析，结果与表5一致。但不同的是，对于稳定点(0,0)，当不考虑噪声时，根据式(3),(6)，强者和弱者的期望收益均为0；当考虑噪声时，根据式(10),(11)，强者和弱者的期望收益均为

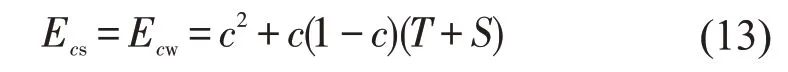
根据式(13)，取噪声c=0.2，绘制强者(弱者)的期望收益Ecs(Ecw)与T，S的取值关系，如图9。从图9可看出，当考虑系统噪声时，强者(弱者)在稳定点(0,0)处获得0.04～0.36之间不等的正收益，说明系统噪声引发一定程度的合作行为，使强者和弱者摆脱因双方背叛而获得惩罚收益P=0 的窘境。

图9 强者(弱者)的期望收益Ecs(Ecw)与T,S 的关系Fig.9 Relationship between the strong(weak)expected payoffs Ecs(Ecw) and T,S

4 结 论

基于社会比较情境下强者和弱者之间产生的同情、欺凌、尊敬、嫉妒4类情感，假设情感与竞合行为之间的映射关系；基于4种博弈模型，建立情感演化的复制动态方程，分析系统演化的平衡点和稳定性，获得不同参数条件下系统的演化机制。在囚徒困境博弈模型(PD模型，1＜T≤2且-1≤S＜0)的框架下，情感系统的演化稳定策略(ESS)为“妒强凌弱”，即强者完全欺凌弱者和弱者完全嫉妒强者，对应的社会系统表现为残酷竞争、自私自利、弱肉强食的黑暗丛林特征。但社会过程显示，“心存敬仰、慷慨大方、宽宏大量”等良性情感和合作行为普遍存在，因此人们应满怀希望，采取以下方法让个体情感和社会系统走向良性。

1)完善制度和规则，通过有效的奖惩鼓励良性情感的发展和演化。通过设定合理的T值与S值，使系统进入猎鹿博弈模型(SH 博弈，0≤T＜1 且0＜S≤1)或雪堆博弈模型(SD 博弈，1＜T≤2 且0＜S≤1)，和谐博弈模型(HG博弈，0≤T＜1且-1≤S＜0)框架，情感系统将获得比囚徒困境博弈模型下相对要好的演化稳定策略。例如：基于猎鹿博弈模型，情感系统的演化稳定策略为强者完全同情弱者和弱者完全尊敬强者的“敬上爱下”；基于雪堆博弈模型，情感系统各50%的机会演化至强者完全同情弱者及弱者完全嫉妒强者的“劫富济贫”模式和强者完全欺凌弱者及弱者完全尊敬强者的“谀上欺下”模式；基于和谐博弈模型，情感系统根据初始状态(良性情感是否占优)决定最终演化为“敬上爱下的天堂”抑或“妒强凌弱的地狱”，因此保持善良的初心很重要。

2)利用文化、宗教、伦理和道德进行社会教化，培养高尚亲和的人格特质，影响群体中其他个体的行为决策。例如[10]个体在做出慈善捐款、志愿者服务等亲社会行为决策时，易受到在品德与喜欢特质上表现突出的高地位他人的影响。

3)强化人际交往和沟通，基于群体角色和社会角色实现相互依存型自我建构，调节社会比较中产生的相应负性情感[20-21]。例如：相互依存关系的自我建构，使好友在某些领域能够纳入自我[22]，产生同化效应(为好友的成功感到高兴而不是嫉妒)；在集体文化中个体更倾向于维护、保持关系与集体中的自我定义[23]，容易产生团体一致性和合作行为。