基于灰色模型的锅炉煤粉细度测量的不确定度评定

张 林，周大慧

(铜陵有色金属集团股份有限公司，安徽铜陵244000)

燃煤发电锅炉是发电厂的三大主机设备之一，目前我国电力生产主要以燃煤发电为主，且会在较长时间内保持这一现状[1]。但煤粉质量标准难以达到要求，导致炉效下降[2]、能耗过高以及粉尘和有害气体大量排放，严重污染环境[3-4]。对于煤粉含量的测量及影响其燃烧的因素目前得到了国内外学者的较多关注，如崔晓钢等[5]提出采用一种具耐磨损、低放射特点的微波测量法测量煤粉含量；刘靖昀[6]分析了氧气含量对煤粉燃烧反应速度、煤粉燃尽率以及废气排放量的影响，得出增加氧气含量可促进煤粉燃尽；陈辉等[7]数值模拟分析不同负荷下煤粉细度对锅炉燃烧的影响，得到低氮燃烧状态下，降低煤粉细度有利于降低飞灰含碳量和省煤器出口NO和NO2的含量；Syrodoy等[8]数值模拟了煤和水煤燃料燃烧产物向内部环境的传热，结果表明煤粉在燃烧过程中形成大量强烈的灰烬沉积。

煤粉细度的适度变化是提高燃煤锅炉燃烧效率的一项重要手段，不同工况条件下使用不同细度的煤粉可有效提高煤粉的燃烧效能。对煤粉细度进行快速准确测量不仅可提高燃煤锅炉的可靠性和稳定性，且具节能减排降本增效的作用[9-10]。煤粉细度的测量主要分为离线测量和在线测量。其中：在线测量以光学测量为代表，测量动态范围大、速度快、重复性较好，但由于在线法测量分辨率较低，不宜测量粒度分布范围较窄的样品，只能测量低准度的工况；离线测量以筛分法为代表，测量原理简单，可相对准确地得到常用筛号下煤粉的细度，同时可客观评价煤粉磨制质量。因此，文中针对小样本、分布类型未知的煤粉细度，基于筛分法建立煤粉细度测量不确定的灰色评定模型，基于灰色模型的不确定度评定方法对煤粉细度进行测量，以期方便准确地对其进行评定。

1 煤粉细度的测量原理

我国锅炉煤粉细度常用孔径为200，90 μm的两种筛子来表示，表示符号分别为R200和R90，其中R90为电厂锅炉运行最常用的控制指标[11-12]。我国采用的筛子规格和煤粉细度表示符号如表1。

表1 常用筛子规格及煤粉细度表示符号Tab.1 Common sieve specifications and pulverized coal fineness indication symbols

使用单一孔径筛子现场检测煤粉细度不能得到准确的结果，磨煤机磨制的煤粉颗粒粒径差异较大，要准确测定煤粉的颗粒平均水平，就需计算煤粉的平均粒径。燃煤电厂的煤粉颗粒特性可用式(1)表示

若R90与R200已知，则

式中：Rx为颗粒尺寸(即煤粉细度)；x 为筛孔孔径；b 为煤粉细度的系数；n 为煤粉均匀性系数，与煤的种类和磨煤方式有关。由式(4)可知：n 越大，煤粉颗粒分布越均匀；n 越小，煤粉颗粒分布越不均匀，存在较多过粗和过细的煤粉。一般n=0.8～1.3，具体取决于磨煤机和分离器的结构[13-14]。

2 煤粉细度不确定度灰色评定模型的建立

2.1 煤粉细度的检验算法

实际测量煤粉细度的过程中，由于无法保证测量在理想情况下进行，导致测量结果存在误差，采用数据预处理技术剔除异值数据，然后按从小到大的顺序排列得到实际煤粉细度检测值数列Z0，如

其中Z0(i)表示第i 次测量时实际煤粉细度检测值。逐次计算式(5)数列Z0(i)的m 项和，得到实际煤粉细度累加数Z1(i)，如

将煤粉细度检测次数i 作为横坐标、前m项和Z1(i)作为纵坐标绘制检测误差分布曲线，结果如图1。图1中：S2表示实际煤粉细度的检测结果；S1表示理想情况下煤粉细度的检测结果。

2.2 检测分散性及不确定度算法

图1中，曲线S1和S2在纵坐标轴方向上的差异Δ(i)反映在重复检测煤粉细度时，由于各种误差而产生检测值的分散性。理想情况下煤粉细度检测过程与实际情况下煤粉细度检测过程的最大分散性用最大距离Δmax表示，如

假设与最大距离Δmax对应的最小横向坐标为m，则Δ(m)＞Δ(m-1)，且Δ(m)≥Δ(m+1)，由于Z0(i) 为递增数列，令为这组数列的平均数，则Z0(i)＜(i=1,2,…,m)，且Z0(i)＞(i=m+1,m+2,…,t)。

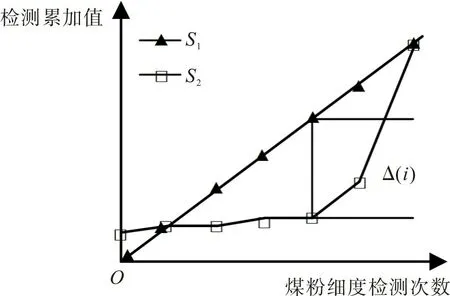
图1 累加检测序列Fig.1 Cumulative detection sequence

令Z1(m)=Z0(i)+…+Z0(m)，则式(7)可转化为式(8)。

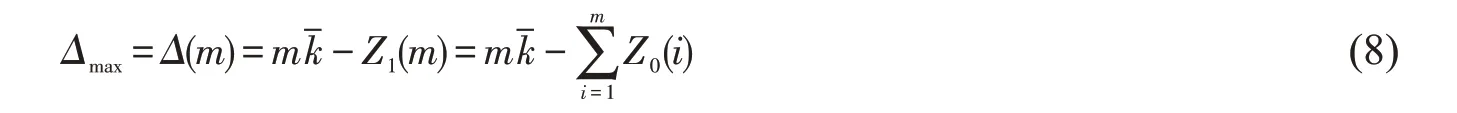
定义灰色标准差SGrey表示煤粉细度检测数据的分散程度，如式(9)

式中：c为示灰色系数；u为一组测量数据总数。参考文献[15]可看出，煤粉细度的分布类型与灰色系数c的关联度不高，通常灰色系数c取2.5，则煤粉细度的灰色不确定度UGrey为

3 实验与结果分析

3.1 煤粉细度的测定

在燃煤电厂采集经磨煤机研磨后的煤粉标本作为检测样本，采用筛分法测量煤粉细度，即把一定量的煤粉放在筛孔尺寸为x的标准筛上筛分，留在筛面上的煤粉质量占原煤粉样总质量的百分数即为煤粉细度Rx。

式中：A为留在筛面煤粉的质量；B为从筛孔掉落煤粉的质量。根据式(11)求出煤粉细度。对同一组样本煤粉细度进行8次测量，去除其中的离群值，得到的煤粉细度如表2。

表2 测定的煤粉细度Tab.2 Measured fineness of pulverized coal

3.2 煤粉细度的评定

3.2.1 不确定度的灰色评定结果

根据表2测定的煤粉细度，采用本文提出的基于灰色模型不确定度评定方法对表中4组数据进行评定。先计算表2中第一组煤粉细度的平均值，后根据步骤2.2找出相差的最大值Δmax，再根据定义的灰色标准差，计算出灰色不确定度。

同理得到另3组煤粉样本细度的不确定度分别为0.130，0.109和0.117，如表3。

3.2.2 不确定度的标准评定

为检验基于灰色模型的不确定度评定方法的评定结果，采用常规的不确定度方法，即标准不确定度的统计评定方法，又称A类不确定度对表2中的4组煤粉细度进行评定。根据式(12)计算出煤粉细度标准差，推导出煤粉细度的标准不确定度，如式(13)。

同理得到另3 组煤粉样本细度的不确定度为0.140，0.130 和0.121，如表3。比较表3 中的数值可知，采用基于灰色模型的不确定度评定方法和标准不确定度的统计评定方法对煤粉细度的不确定度进行评定，两种方法的评定结果无显著性差异，验证了灰色模型在评定煤粉细度不确定度是科学可行的。与标准不确定度的统计评定方法相比，基于灰色模型的不确定度评定方法中，计算煤粉细度Δmax的过程相对简单方便，对煤粉细度不确定度评定速度较快。

表3 灰色不确定度和标准不确定度的对比Tab.3 Comparison between grey uncertainty and standard uncertainty

3.3 实际工况应用

煤粉燃烧的不完全损失对实际工况有重要影响，煤粉细度是煤粉燃烧损失的主要作用因素。为研究煤粉细度变化对燃煤锅炉燃烧的影响，进行燃煤燃烧优化实验，实验条件如表4。

表4 煤粉细度变化对燃烧特性影响的实验条件Tab.4 Experimental conditions for the influence of fineness of pulverized coal on combustion characteristics

实验过程中，在燃煤锅炉着火壁温1 320 ℃、给粉量143 g·h-1、配风量1.01 m3·h-1的条件下，改变煤粉细度，测量煤粉细度变化时的飞灰含碳量。测量结果为：煤粉细度R90的质量分数为24%时，飞灰含碳量为7.21%(质量分数，下同)；煤粉细度R90的质量分数为15%时，飞灰含碳量为6.24%，煤粉细度R90的质量分数为6%时，飞灰含碳量降低到0.45%。由此可见：煤粉细度R90的质量分数为6%时，煤粉燃烧效果较为理想；在燃煤锅炉着火壁温、给粉量、配风量条件确定时，通过测量飞灰含碳量可得燃烧时的最佳煤粉细度。在已知最佳煤粉细度时，需尽量避免不完全燃烧时的损失，依据采用灰色模型不确定度对煤粉细度的评定结果，对锅炉燃烧过程进行相应调整，可使锅炉保持最佳燃烧工况，提高燃煤锅炉的经济运行效率。

4 结 论

针对煤粉细度的不确定度，提出一种基于灰色模型的不确定度测量方法，对煤粉细度数据的不确定度进行评定。结果表明：煤粉细度不确定度的灰色评定值与标准评定结果相比无显著性差异，验证了灰色模型在评定煤粉细度不确定度是科学可行的，且灰色不确定度准确度高、简单易行。可根据准确度明确的煤粉细度，指导运行人员适时调整燃烧过程，使锅炉保持最佳燃烧工况，提高燃煤锅炉的经济运行效率。