考虑化学腐蚀作用的砂板岩损伤本构模型
2020-12-26刘志航李雪浩
刘志航,王 伟,李雪浩,李 尧,王 辉
(1.河海大学a.岩土力学与堤坝工程教育部重点实验室;b.土木与交通学院岩土所,江苏南京210098;2.山西省交通规划勘察设计院,山西太原030012)
当前环境问题日益严峻,岩体赋存的水环境越来越复杂,酸雨、受污染的地下水及地表水等对岩体腐蚀的现象也越来越多。水岩之间的相互作用会影响岩体的强度与稳定性[1],甚至会造成工程事故。针对这一现状,众多学者开展了水岩相互作用的研究,对经化学溶液浸泡后的砂岩进行压缩试验,分析浸泡试样的力学特性[2-3]、细观结构以及溶液成分[4]等。Xie等[5]分别对自然状态和经化学腐蚀的多孔石灰岩进行三轴试验,发现化学腐蚀会减小石灰岩孔隙率,从而降低其黏聚力与弹性模量。工程中常见的板岩在化学腐蚀作用后,岩石内部胶结物除发生化学反应还会发生剧烈水解反应,溶蚀效应较大,颗粒大量流失,孔隙与裂隙逐渐发育,矿物颗粒间的接触面减少,岩石的宏观性能也发生了改变,使得岩石强度降低。因此研究化学腐蚀作用下砂板岩的性质具有重要的工程意义。
Hu等[6]以化学动力学为基础,提出了考虑应力路径和化学损伤双重影响的耦合弹塑性模型;邓华峰等[7]以浸泡-风干循环水岩作用的砂岩试验数据为基础,将损伤效应耦合到统计本构模型中,建立了水岩作用下砂岩的统计损伤本构模型,但该本构模型未考虑损伤阈值的影响;姜立春等[8]基于统计损伤理论,提出了考虑矿山酸性排泄水蚀化和应力耦合影响的砂岩损伤本构模型;刘建等[9]采用改进的Duncan模型模拟不同水溶液作用下砂岩的应力应变曲线;夏冬等[10]基于饱水闪长岩在不同浸水时间下的单轴压缩声发射试验结果,建立了与浸水时间相关的声发射损伤模型,但并未对应力应变曲线进行研究。上述本构模型研究对象主要是砂岩等,针对砂板岩这种孔隙多、单轴条件下压密效应明显、塑性变形差[11]的岩石考虑较少。因此,文中以砂板岩为研究对象,采用文献[11]中的试验数据,引入损伤力学方法,建立化学腐蚀后砂板岩的分段单轴压缩统计损伤本构模型,将模型分段处理,并通过具体试验数据进行验证,其研究结果对化学腐蚀作用下砂板岩的力学性能研究具有一定意义。
1 统计损伤本构模型的建立
1.1 耦合损伤变量
岩石材料的损伤会引起其微观与宏观方面某些性质的改变,因此可从不同角度对损伤变量进行相应定义。根据文献[12-14],岩石受化学腐蚀作用后,其弹性模量、抗剪强度、抗压强度、孔隙率等均有不同程度的下降,产生一个初始化学损伤值,相应的化学损伤变量D1可定义如下[15]

式中:Et为经历不同化学腐蚀时间后岩石的弹性模量;E0为未受化学腐蚀岩石的弹性模量。
在外荷载的作用下,岩石内部的力学性质是随机分布的,由此带来的微损伤也是随机分布的,可采用统计学的方法描述这种力学性质。假设岩石中微元的破坏服从Weibull分布,相应的概率密度函数φ(ε)如下[16]

式中:m,ε0为Weibull统计分布参数;ε 为岩石材料应变。当岩石被加载到应变水平ε 时,对式(2)进行积分得相应的受荷损伤变量D2,表达式如下

结合式(1),(3)得到同时考虑化学损伤与受荷损伤的耦合损伤D 表达式[8],如
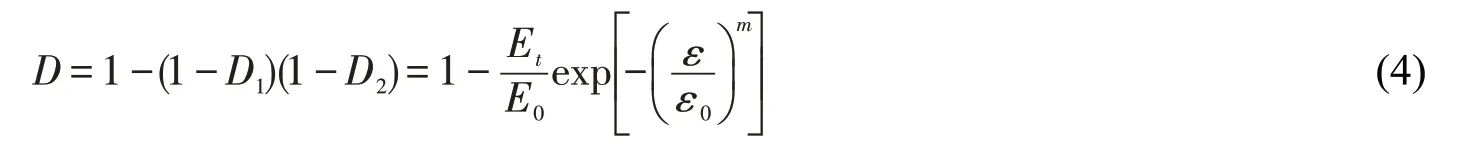
1.2 损伤模型
根据Lemaitre提出的应变等价原理[17],假设损伤各向同性,结合文献[8]中推广后的应变等价原理,以岩石的天然损伤状态为第1状态,以岩石腐蚀后并加荷的损伤状态为第2状态,可得推广后名义应力与有效应力之间的关系:

式中:[σ*] 为有效应力矩阵;[σ ] 为名义应力矩阵。
引用的试验采用单轴压缩方法[11],为方便理解计算,可根据广义胡克定律与式(5)推导出考虑耦合损伤的单轴条件下本构关系:

式中:σ 与ε 分别表示轴向应力与轴向应变。将式(4)代入式(6),可得考虑耦合损伤的砂板岩单轴压缩统计本构模型:



式中:σe与εe分别为不同腐蚀时间下试验曲线弹性阶段起点对应的应力与应变;σp与εp分别为弹性阶段终点对应的应力与应变;m1,ε01,m2,ε02为统计分布参数,下标用于区分不同阶段。式(8)第一式为压密阶段的模型,仅采用相应的形式来表征压密阶段试验曲线的变形特征;受荷损伤是从屈服阶段开始的,但单轴下砂板岩塑性变形不明显,很难分辨出变化,通过分段的方法将式(8)第三式起点移至(εp,σp),“放大”了塑性阶段的变化,用相应的参数体现开展程度,研究浸泡时间对岩样延性的影响。此法会使得峰后出现一个“人为残余强度”,但单轴条件下砂板岩峰后变形较差,试验值较难测得,研究意义不大。故文中重点分析砂板岩峰前尤其是压密至线弹性阶段的应力应变曲线。
2 模型参数的确定与验证
2.1 参数确定
统计本构模型的关键在于分布参数的选取,通常用两种方法确定分布参数:试验数据线性拟合法[7];试验曲线极值法[18]。模型第一段对应压密阶段,数据较丰富,宜采用线性拟合的方法;砂板岩脆性较强,单轴下塑性变形不明显,且达到峰值强度后迅速降低,对于峰后试验数据采集较少,为模拟砂板岩的塑性变形,第三段参数宜采用试验曲线极值法。
1)当0 ≤ε ≤εe时,将式(8)第一式进行变形可得

对两边同时取对数得

再进行移项然后两边取对数得
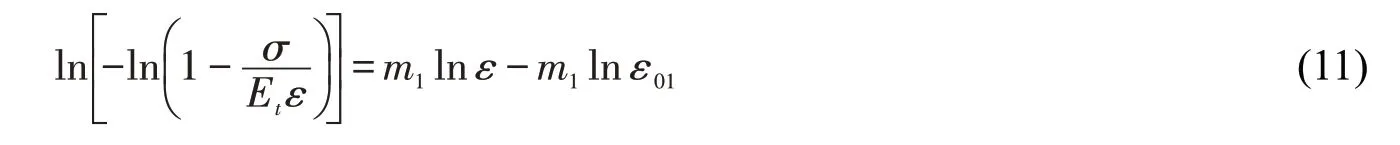

压密阶段选取使Y 与X 能够较好呈现线性段的试验数据进行线性拟合,得到相应参数m1与ε01的值。
2)当ε >εp时,试验曲线在峰值处应力最大,因此峰值处的应力应变当满足以下条件
式中σc与εc为不同腐蚀时间下试验曲线峰值应力与峰值应变。将上述条件代入式(8)第三式,偏导可得

根据式(8)第三式与式(14)可得参数m2与ε02的值:

模型中σe,εe,σp,εp为不同腐蚀时间岩石试验曲线上特定的应力与应变,先找寻近似直线段作为弹性阶段,其平均斜率为弹性模量Et;σe与εe为该近似直线段起点对应的应力与应变,σp与εp为该近似直线段终点对应的应力与应变,从而确定相关分布参数。
2.2 试验验证
由于篇幅的限制,文中选用文献[11]中pH=4酸性溶液腐蚀砂板岩的单轴压缩试验部分结果,验证所建模型的合理性与适用性。根据式(12)与式(15)得到的统计分布参数如表1,砂板岩单轴分段模型曲线与试验曲线见图1,浸泡时间为0 d的是天然试样。
从图1可看出:砂板岩初始孔隙较多,压密效应占比明显,表明将压密段单独考虑较为合适;砂板岩塑性变形较差,弹性模量降低不明显,但峰值强度的降低与峰值应变的增加表现出化学腐蚀作用对岩样的软化效应。
将图1中试验数据与分段模拟结果进行对比可以看出:所建统计损伤本构模型曲线与试验曲线较为相符,表明文中所建模型能够较好地反映化学腐蚀作用下砂板岩峰前应力应变关系;浸泡初期岩样较脆,天然试样与浸泡10 d的试样在压缩过程中弹性模量降低不明显,同时实际屈服点与峰值点相隔较近,塑性阶段占比较少,没有明显的塑性屈服阶段,从而使得在选取近似直线段作为弹性阶段时,易将不明显的塑性屈服阶段划至弹性阶段内,峰值点与屈服点被认为“重合”,无法用式(15)进行参数计算,因此表1 中天然试样与浸泡10 d 的试样第三段参数无法得出;对于全过程应力应变曲线,随着浸泡时间的延长,峰值应变逐渐增大,砂板岩脆性降低,延性增加,根据第三段Weibull参数,塑性变形的程度依旧很小,浸泡180 d 岩样的塑性变形依然不明显,当达到峰值应力时岩样迅速破坏。

表1 砂板岩损伤本构模型统计分布参数Tab.1 Statistical distribution parameters of damage constitutive model of sandy slate

图1 砂板岩模型曲线与试验曲线Fig.1 Model curves and test curves of sandy slate
综上,文中以试验曲线压密点与屈服点建立的分段模型可模拟砂板岩在峰前压密至线弹性阶段的本构关系,验证了模型的合理性与适用性。但由于砂板岩单轴条件下塑性变形较差,没有明显的塑性阶段,其塑性阶段以及峰后软化阶段的试验曲线较难获得,对模拟峰值应力改变与峰后的跌落情况,达不到与其他浸泡岩样相同的模拟效果。因此,对于化学腐蚀作用下砂板岩的损伤本构关系还需进一步分析。
3 模型的修正
砂板岩塑性变形阶段模拟达不到理想的效果,但文中对于压密阶段至弹性阶段的考虑可为塑性变形较好的岩样提供参考。对于常见的砂岩等,塑性变形较好,压密至线弹性阶段可采用式(8)第一式与第二式进行模拟。砂岩塑性变形较好,峰后软化试验曲线较易得到,若采用式(8)第三式进行模拟,会产生“人为残余强度”。因此,参考文献[18,20],将式(8)第三式进行修正,具体表达式与参数计算式如下:
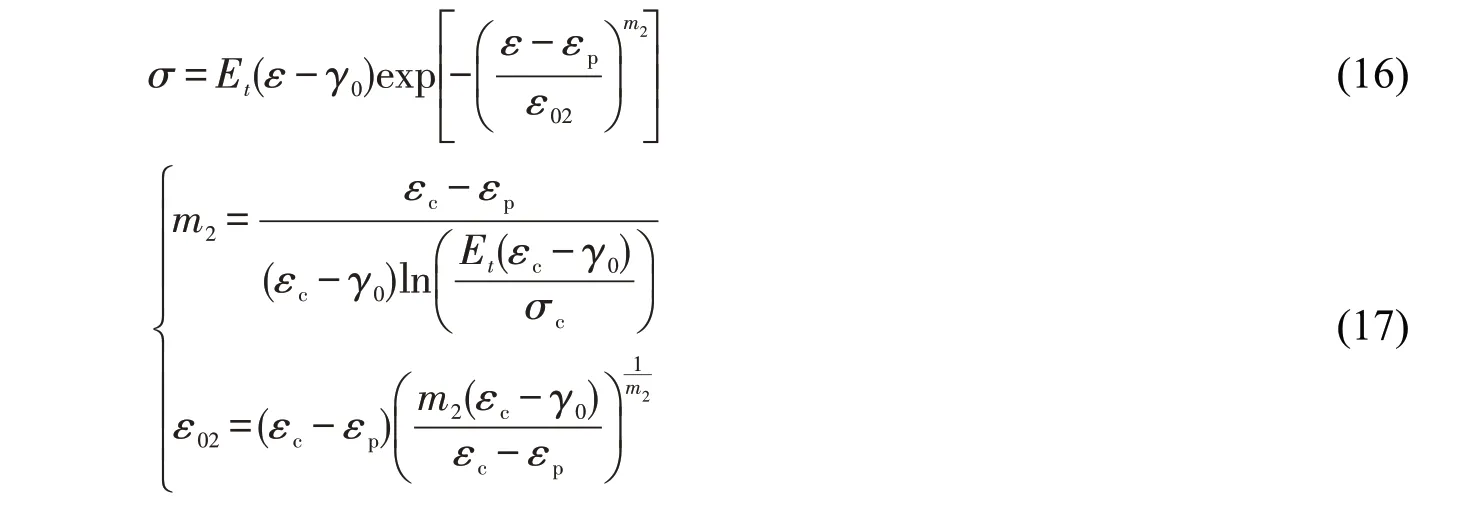
式中γ0为不同腐蚀时间下单轴压缩试验曲线弹性阶段直线延长至应变轴对应的截距[20]。式(16)中减去γ0是为了消除初始孔隙压密带来的应变,式(17)同式(15)采用试验曲线极值法推导。
为验证修正模型的适用性,选取pH=1酸性溶液腐蚀砂岩的单轴压缩试验部分数据[21],未修正与修正模型参数见表2,模拟结果与试验结果如图2。

表2 砂岩损伤本构模型统计分布参数Tab.2 Statistical distribution parameters of damage constitutive model of sandstone
从图2 可看出:本文建立的修正模型在峰前能够较好地模拟砂岩应力应变关系,峰后也能展现下降趋势,虽吻合程度不太理想,但修正模型曲线更接近试验曲线;化学腐蚀对岩样造成一定损伤,浸泡9 d的岩样在加载中途产生局部破坏,应力突降,因此表2 中第三段的参数规律有差异,但从模拟结果看效果较好。

图2 砂岩模拟结果与试验结果比较Fig.2 Comparison between simulation value and test value of sandstone
4 结 论
1)假设经化学腐蚀的岩石受荷后微元的破坏服从Weibull 分布,结合耦合损伤作用与压密效应,以试验曲线压密点与屈服点建立分段模型,采用试验数据线性拟合法与试验曲线极值法综合确定不同阶段的统计分布参数,建立的分段模型可模拟砂板岩峰前压密至线弹性阶段的本构关系,但塑性阶段及峰后模拟达不到理想效果。
2)修正建立的分段模型第三段,消除了由于分段造成的“人为残余强度”,使本构模型更加接近试验数据,提高了模型的合理性与适用性,为后续研究奠定了相应基础。
