我国小学生计算思维量表研发与应用

张屹 莫尉 张岩 高晗蕊 李妞 林郁菲

摘要：随着计算思维相关研究的日益升温，全球计算思维培养呈现出“低龄化”和“跨学科”的整体发展趋势。针对目前缺乏小学阶段计算思维量表的研究现状，该研究通过对844名小学生问卷调查，综合运用探索性因素分析和验证性因素分析方法，编制了我国小学生计算思维量表;并采用多组验证性分析，检验了该量表跨性别、跨年级水平的测量等值性。研究结果显示：最终量表共包含23个测量项目，分属于创造力、批判思维、问题解决能力、算法思维、合作能力等五个维度，五个维度可以有效地聚合到计算思维二阶因子上。该量表克隆巴赫系数达0.928，各维度平均方差萃取量（AVE）在0.506-0.725之间，满足跨性别和跨年级水平的严格等值性。综合研究结果表明，该量表具有良好的信效度，可用于我国小学生群体计算思维能力评测。最后，研究对我国小学生计算思维量表进行了初步应用，结果发现：小学生计算思维能力在高、中年级水平与性别间均不存在显著差异;计算思维能力能够显著预测学生数学和语文学业成绩，且其影响存在学科差异。

关键词：小学生;计算思维;量表;等值性检验;影响因素;学业成绩

中图分类号：G434

文獻标识码：A

随着计算机、信息技术的发展，人们的社会生活发生着日新月异的变化。面向未来的教育，应是让学生为迎接未来的生活做好准备，让他们有能力使用目前还未发明的技术来解决未来的问题[1]。为此，卡梅隆大学周以真教授2006年重新描述了Papert于1980年提出的计算思维（ComputationalThinking）概念，将其定义为“运用计算机科学的基础概念进行问题求解、系统设计以及人类行为理解等涵盖计算机科学之广度的一系列思维活动”[2]，为信息化时代的问题解决增加了新的内涵。自该概念提出以来，计算思维获得了全球范围的广泛关注，被认为是一项“每个人都应该学会与使用的一种应用态度与技能”[3]，对于为未来世界做好准备至关重要。

为“确保所有人理解和应用计算思维提供一个共同而坚实的基础”[4]，将有效、公平的计算思维教育引入小学阶段便显得十分必要。目前，全球计算思维培养已呈现出“低龄化”和“跨学科”的整体发展趋势[5]。我国在《高中信息技术课程标准》中将计算思维确立为信息技术学科四大核心素养之一[6]，并采取了系列举措着力推动计算思维培养向中小学阶段的过渡。美国、新加坡、澳大利亚、欧洲各国等均在K12人才培养计划和课程体系中纳入计算思维相关内容。同时，发展心理学的研究结果已确切表明，小学生不能被简单地看作是较年长青年的能力较弱版本，他们有其特殊的认知特点与学习需求，应当在教学及相应的评价过程中适当地反映出来[7]。然而，作为近年来才被广泛关注的概念，目前关于小学生计算思维发展特点的研究还较少，更加缺乏具有针对性的评价量规，为计算思维教育的开展带来障碍。基于此，本研究将在现有研究基础上：（1）按照科学的量表编制程序，开发小学生计算思维量表;（2）在对所开发量表的跨性别及跨年级水平测量等值性检验的基础上，探讨影响小学生计算思维的因素;（3）探索计算思维能力对学生学业成绩的影响。旨在为后续相关研究做更深入的探讨提供理论参考及工具支持。

一、文献综述

（一）计算思维定义及概念维度

目前，国内外研究者们围绕计算思维定义的讨论，分为狭义层面和广义层面两种脉络。狭义层面突出强调计算思维与具体学科的关系，认为计算思维是通过使用编程、高效率专用算法和数值分析培养起来的心智习惯[8][9]，在不同学科领域内表现出独特内涵[10]。广义层面概念则抽象于具体学科外，倾向于计算思维的通用化和普适性，认为计算思维是在形成问题及其快速有效解决方案时所必备的思维能力[11]。其中，美国国际教育技术协会（简称ISTE）2015年提出的定义是较为典型的代表，认为计算思维是能够“有效结合数字技术与人类思想，解决复杂现实问题的一系列心智工具集”[l2]。在该广义定义的基础上，为深入分析概念内涵和结构表征，ISTE联合美国计算机科学教师协会（简称CSTA）及美国国家科学基金会（简称NSF）在一项旨在指导K-12阶段教育者如何帮助学生获得计算思维技能的项目中，拟定了计算思维通用框架[13]。框架从能力观的角度出发，将计算思维视为包含创造力、算法思维、批判性思维、问题解决、合作能力及其相互作用的复合能力，为教育者在所有年级和所有学科领域教授计算思维提供理论依据，是对计算思维进行的最为全面的解析。在此框架基础上，可以脱离编程环境开展研究与讨论，适宜于作为计算思维通用测评量表开发的理论依据，从而为大范围了解特定对象群体计算思维整体状况奠定基础。

（二）计算思维量表研究

计算思维的测量一直是该研究领域的难点，特别是针对计算思维的量表开发处于较滞后的状态。现有计算思维量表编制主要以更成熟的群体为研究对象，尚缺少针对小学生群体的计算思维量表。土耳其研究者Korkmaz等人在2017年编制了计算思维量表CTS[14]，该量表能够实现对大学生计算思维的测量，是目前国际上使用和引证最为广泛的量表。Korkmaz还针对初中学生编制了计算思维量表CTLS[15]，该量表与CTs-样包含创造力、批判思维、问题解决能力、算法思维、合作能力等5个维度，但在CTs的基础上从29道题缩减为22题。与CTs相比，CTLS更加凸显中学的情境性及被试群体特点。华东师大顾小清团队在CTLS量表基础上进行了汉化[16]，对量表信效度进行了较为全面的检验，验证了在高中阶段的适用性。本研究也曾在CTs的基础上进行本土化研究，但该量表所选用的分维度量表与小学生群体的认知水平、教育情境相差较大，经两轮迭代修订后问卷信效度仍难以通过检验。这也证明了计算思维在不同教育阶段具有其独特性的表现，针对小学阶段，编制适当量表是具有理论与实践意义的研究工作。

（三）性别、年级水平等因素对计算思维的影响研究

分析学习者计算思维影响因素是制定相关教育政策、设计具有针对性教学策略的前提。现有研究探讨了性别、年级水平对计算思维能力的影响。Atmatzidou[17]结合问卷调查与质性分析，对初、高中生计算思维水平进行研究，发现男女生之间不存在显著差异，且初中和高中组的整体计算思维能力处于相同水平，仅在分解、一般化等分维度上表现出与认知成熟度相关的差异。Werner[18]对10-14岁学生在游戏编程任务中的计算思维表现进行评估，也未发现计算思维能力与性别、年级水平存在相关性。但另一些研究则有不同结论。白雪梅、顾小清[19]通过问卷调查发现我国高中男生计算思维能力显著高于同年级女生，同时随着年级水平的提高计算思维能力显著下降。Roman_Gonzalez[20]通过CTT测试考察西班牙学生计算思维概念水平，研究表明中小学男女生之间存在差异，并发现5-6年级与7-8年级没有编程经验的学生计算思维能力与年级水平为正相关关系。Seiter等人[21]对150名一到六年级小学生编写的程序进行分析，发现计算思维概念应用的熟练程度随年级水平增长的趋势。由此可见，现有研究结论未呈现一致性，且性别、年级水平对小学生群体的影响展现出与青年和成年学习者不同的特征。众说纷纭的研究结果，一方面说明了学习计算思维技能的过程对于不同年级、性别的学生而言都是一项挑战，另一方面也说明了需要从计算思维评价工具的科学性人手，进一步确定性别、年级水平对计算思维能力的影响程度和差异。

二、小学生计算思维量表编制、预测试及项目分析

（一）量表编制

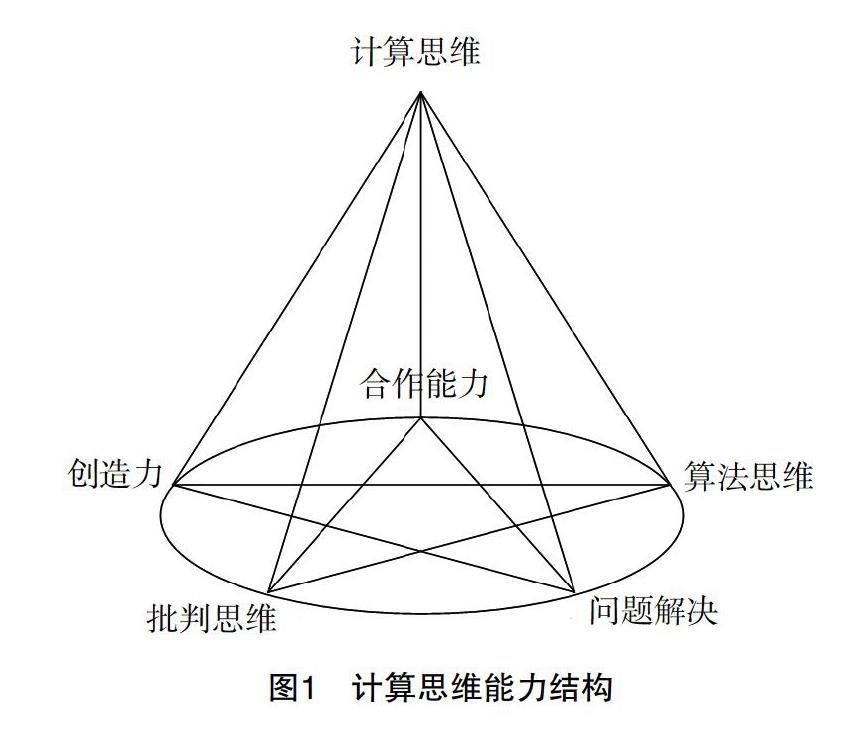
为克服计算思维研究中的挑战，Weintrop等人建议“有必要将计算思维分解为一组定义明确且可衡量的技能、概念或实践”[22]。因此，本研究采用ISTE五维能力框架，将计算思维理解为：在计算任务和活动中，所涉及的相关认知技能的概括性集合。形成如下页图1所示的计算思维能力结构图。

首先，（1）在创造力维度关注学生从事创造性活动时的认知过程，包括：针对特定问题产生大量想法和思路的能力;考虑特定项目尽可能多的用途的能力;产生具有独创性想法的能力;通过与新想法结合，扩充和改进已有方案的能力。（2）小学生处于批判思维能力启蒙阶段，主要表现在评价、分析能力的提升以及抽象、推理和归纳能力的发生。因此，应着重关注学生塑造和评估自己想法的过程，从寻找真相、开放思想、分析能力、系统化能力等角度进行评价。（3）问题解决能力维度主要考察学习者问题解决策略的使用，通过判断在问题分类、问题理解、问题处理方式等方面的差异来确定小学生问题解决能力水平。（4）本研究将算法思维界定为个人在解决问题的过程中详尽列出解决方案步骤的认知过程。结合小学教育特点，简化“算法可解性”的要求，侧重于评价学生对数据处理流程和数据间关系的把握，以及是否具有“一种解决问题的步骤可以用于解决一系列类似问题”的意识。（5）本研究综合教育领域相关研究的主流观点，认为“合作能力”是小组活动和团队任务中个体的人际交往能力或社交技能，包含合作意识、合作技能、合作品质。

以上述小学生计算思维各维度分析为基础，本研究通过查阅文献和咨询专家意见，进行了量表题项的初步编制。为确保量表的信度和效度，各维度题项通过直接引用或改编已有成熟评价项目的方式完成。题项首先由1位教育技术学博士生及2位教育技术学硕士生进行单独选择，然后对所选项目进行比较，并达成共识。接着，采用专家法进行所选题项内容效度检验。专家组由5人构成，包括3位高校教育信息技术领域专家（教授、副教授、讲师各1位），1位中小学信息技术教研员以及1位教育技术学在读博士生。语言评估由1位小学语文教师辅助研究者进行。最后遴选出42道测试题项，均采用Likert 5点计分。各维度具体参照如表1所示。

（二）量表预测试

本研究通过预测试及项目分析，初步检验量表中各题项的适用性，包括题项的鉴别度检验及题目表述的修订。从我国小学计算思维培养实施现状来看，主要依托于信息技术、科学、数学、综合实践等含STEM主题的课程进行[28]。为保证量表的适切性及样本数据的代表性，本研究预试选取我国中部地区H省W市A实验小学进行，该校近年来通过常规课堂、社团课程等形式开展了丰富多彩的STEM类校本课程。本研究随机选取了三年级及五年级各一个自然班学生共120人为研究对象，采用问卷星进行预测问卷在线填答，回收有效问卷113份，其中男生62名，女生51名。

对回收的预测问卷采用临界比值法（CriticalRation）进行鉴别度检验[29]，以剔除鉴别度不符合要求的测量题项。经分析，PP1和PP8两题临界比值未达到显著性差异，即题项不具有鉴别度，予以删除。随后，对剩余的40个题项计算题总相关，以考察各题项与所对应的分量表总分的相关度。分析结果显示各题项题总相关系数在0.441-0.830之间，均在p<0.001水平达到显著，故40个题项均予以保留。此外，预测施测后还收集了预测对象对于题项表述理解的问题，以便对问卷作进一步修订。由此，形成包含40道测量题项的初步施测量表。

三、小学生计算思维量表结构探索与验证

在问卷预测试的基础上，为进一步精炼题项，確保问卷的适切性。本研究选取另一样本群体进行正式施测，分别利用统计软件SPSS 23和Mplus 7，通过探索性因素分析、验证性因素分析对编制的“小学生计算思维量表”结构进行分析。

（一）研究对象情况

现有研究表明，从小学三年级开始学生对计算思维概念有了全面的初步了解[30]。因此，本研究正式施测采用整群抽样的方法，选取与预测对象同区域同层次的Z实验校，对三到六年级共908名学生进行整群施测，研究对象年龄范围为9-12岁。正式施测通过问卷星进行在线发放，组织被试现场集中填答。共回收有效问卷844份，其中男生421名，占49.9%，女生423名，占50.1%。三年级学生171人，占20.3%;四年级学生242人，占28.6%;五年级学生232人，占27.5%;六年级学生199人，占23.6%。正式测试样本数据被随机分半，一半（N=422）用于探索性因素分析，另一半（N=422）用于验证性因素分析。

（二）量表结构的探索性分析

本研究首先通过探索性因素分析对小学生计算思维量表的结构进行探索。样本数据KMO值为0.962，Bartlett球形检验达到显著，说明适合进行因素分析。具体分析采用斜交旋转及主成分分析法进行。依据研究者提出的判定准则[31]，剔除因子负荷低于0.5以及两个因子之间负荷差异不小于0.1的项目。经多轮探索性分析后，综合特征值大于1、解释方差总量、碎石图等准则，最终提取出五个因子。各因子下属题项的含义一致，不存在命名困难，分别为：创造力、批判性思维、问题解决、算法思维和合作能力，共包含23个测量项目，各测量项目的因子负荷均在0.662以上。具体分析结果如表2所示。

（三）量表结构的验证性分析

在探索性因素分析结果的基础上，本研究对另一半样本数据进行验证性因素分析。其中，一阶验证性因素分析用以检验小学生计算思维量表的五因子结构拟合程度，二阶验证性因素分析用以检验计算思维能力结构的合理性。

从表3及下页图2所示的一阶验证性因素分析各项参数结果来看，拟合指数符合X 2/df<5，RMSEA<0.08，CFI>0.9，TLI>0.9，SRMR<0.08的理想标准，模型对数据拟合良好。说明验证性因素分析支持探索性因素分析得出的小学生计算思维量表的五因子结构模型，修订后的包含23个题项的小学生计算思维量表具有良好的结构。

依据计算思维能力结构理论，计算思维由创造力、批判思维能力、问题解决能力、算法思维、合作能力相互作用的复合能力组成。为验证该理论，本研究采用二阶验证性因素分析，来检验是否能使用一个高阶因子（计算思维）去解释上述五种能力。判断二阶因子是否成立，包括两项标准[32]： （1）二阶负荷较高;（2）与一阶模型相比，二阶模型未显著恶化。

从表3及下页图2所示结果可以看出，在二阶因子模型中，五个标准化二阶负荷取值在0.740-0.932之间，说明二阶因子与五个一阶因子间拥有较强的关系。同时，采用似然比检验二阶因子模型是否在一阶因子模型基础上存在恶化，分析结果为△X 2 =13.34<15.09（a=0.01），证明差异不显著，即二阶模型没有显著恶化模型拟合，且从各项拟合指数以及信息指数AIC和BIC来看，二阶模型与一阶模型相差无几。由此，通过二阶模型验证了创造力、批判思维能力、问题解决能力、算法思维以及合作能力间的相关，能够由一个高阶因子（即计算思维）去解释。计算思维能力结构模型具有理论和实证上的合理性。

综上所述，本研究在初步问卷编制的基础上，面向小学生群体展开了第两轮调研。结合探索性因素分析及验证性因素分析法，对量表所获得的数据结构进行了严格的筛选和检验。最终确定包含创造力、批判思维能力、问题解决能力、算法思维、合作能力五维度的计算思维模型在小学生群体中的适用性，形成了包含23道题项的我国小学生计算思维正式量表。

四、小学生计算思维量表质量检验

（一）量表信效度分析

依据探索性因素分析计算出的各测量题项的因子负荷量，对小学生计算思维量表的信度与效度做进一步分析。通常采用克隆巴赫a系数（CronbachIsa）和组合信度（CR值）指标作为信度的度量，当大于0.7时表示量表信度良好。经分析，计算思维总量表Cronbach's a系数为0.928，创造力、问题解决、算法思维、合作能力等维度的CronbachIs a均大于0.8。批判思维维度Cronbach's a 系数值稍低于0.7，但该维度的组合信度指标值达0.784，表明该维度内部一致性在可接受范围。因此，综合考虑各项信度指标，小学生计算思维量表的信度达到要求，说明利用该量表获得的测评结果具有良好的一致性、稳定性和可靠性。效度检验包括收敛效度和区分效度。收敛效度表示测量同一维度的题项之间的相关程度，区分效度表示不同维度间的差异程度。本研究采用平均方差萃取量（AVE值）检验收敛效度以及AVE的平方根检验区分效度。经分析，小学生计算思维量表的AVE值在0.506-0.725之间（均大于0.5），表明测量模型具有良好的收敛效度。此外，依照Follnell-Larcker准则，各维度AVE平方根值均大于维度间皮尔逊相关，表示量表具有良好的区别效度。综上所述，说明了小学生计算思维量表中各维度都紧密围绕所属特质，各维度在计算思维整体中具有独立的作用，验证了本研究所编制的小学生计算思维量表的可接受性。

（二）测量等值性检验

测量等值性检验是考察量表结构在不同学生群体中的适用性，是进行不同学生群体间计算思维能力水平差异比较的前提。

为检验本研究所编制的小学生计算思维量表是否具有跨性别、跨年级水平的测量等值性，我们采用多组验证性因素分析，通过分别比较男女生分组、中年段（三、四年级）与高年段（五、六年级）分组下列五个嵌套模型之间的差异来实现：形态等值（Model 1，基线模型），即检验不同群组之间潜变量與指标的从属关系相同;弱等值（Model 2），即检验因子负荷在各组间是否相等;强等值（Model 3），即检验各组间观测变量的截距是否相等;因子方差协方差等值（Model 4）;严格等值（Model 5），即检验不同群组之间误差方差是否相等。当嵌套模型间的差异值满足相应统计要求时，即认为量表满足所对应的等值类型。本研究运用MPlus7软件进行上述统计分析，选用稳健极大似然估计方法（MLR）对全部844份问卷样本进行数据分析。采用卡方差异检验、模型拟合指数CFI、TLI的差异（△CFI、△TLI）以及贝叶斯信息准则（BIC）来评估测量等值性。分析结果表明，各模型均达理想的拟合水平，性别等值性、年级水平等值性分析均满足严格等值（Model5）要求（X2/df﹤5， TLI>0.9， CFI>0.9， RMSEA<0.08，SRMR<0.08，△X2/A df<5，△TLI

五、小學生计算思维量表应用

（一）小学生计算思维总体状况

我国小学生计算思维总体状况如表4所示，学生计算思维能力水平最低得分为25.33分，最高得分为100分，平均值为84.8分。整体而言，我国小学生计算思维水平处于较高水平。从计算思维各分维度来看，学生的得分均值从高到低依次为：合作能力（86.37）、创造力（85.85）、批判思维（85.32）、问题解决能力（84.18）、算法思维（82.30），即我国小学生计算思维水平各维度中，合作能力水平最高，算法思维和问题解决能力相对较弱。

（二）性别、年级水平等因素对小学生计算思维的影响研究

本研究利用结构方程模型中的均值结构模型对潜变量的组间均值进行差异比较。小学生计算思维水平性别差异情况如表5所示。从结果可知，以计算思维整体能力而言，女生的得分略高于男生，但无显著差异。在分维度方面，女生的合作能力和问题解决能力显著高于男生。男生则在算法思维上表现出优于女生的趋势。

小学生计算思维能力在年级水平上的差异，由表6结果所示。不同年级水平学生间的计算思维整体能力未见显著差异，但中年级段得分略高于高年级段。进一步分析发现，中年级段学生的算法思维感知度显著高于高年级学生。高年段学生在批判性思维和问题解决能力上得分高于中年段学生，但不存在显著性差异。

（三）小学生计算思维能力对学业成绩的影响分析

本研究采用结构方程模型，分析正式施测中四一六年级学生计算思维能力对学期末标准化测验中数学和语文成绩的影响（因施测学校课程考试改革，三年级无测验成绩）。分析过程分两步完成，首先分析了作为二阶因子的小学生计算思维整体能力对数学、语文成绩的影响，继而分析了计算思维各子维度与数学、语文成绩的关系。结构模型分析结果如图3所示。

通过图3中标准化路径系数及其显著性值可知，计算思维能力与数学成绩（β=0.168，P

六、研究结论与展望

（一）研究结论

1.本研究所提出的我国小学生计算思维量表开发过程科学、量表结构合理，可用于评估中国小学生计算思维水平。本研究从计算思维广义概念视角出发，以ISTE提出的计算思维能力结构为理论基础，依据量表编制标准化流程，通过文献分析、专家论证以及两轮调研，综合探索性因素分析和验证性因素分析方法，最终确定了包含创造力、批判思维、问题解决能力、算法思维、合作能力等五个子维度，由23个测量题项组成的我国小学生计算思维量表。该量表信度、收敛效度和区别效度均符合心理测量学标准，在性别及年级水平等值性上满足严格等值要求。综上，该量表适宜于在编程与非编程环境下对我国小学生计算思维能力进行测量，并可通过观测分数对不同性别、不同年级水平小学生的计算思维能力进行跨组差异比较。同时，本研究从文献支持和实证意义的角度验证了ISTE计算思维能力结构划分的合理性，进一步说明了培养计算思维的深层次意义在于，通过调动学习者的问题解决能力、创造力、批判思维、算法思维、合作能力等多种能力促使其普通思维方式发生变化。

2.我国小学生计算思维水平整体较高，在分维度上，学生的合作能力水平最高，算法思维和问题解决能力相对较弱。自2016年我国发布《教育信息化“十三五”规划》以来，作为培养学生计算思维重要载体的STEM教育、编程教育，在我国经历了从萌芽到逐步普及的发展过程[33]。我国小学生计算思维水平整体处于较高水平，得益于近年来以跨学科特性和问题解决为导向的STEM教育、编程教育的良好开展。在计算思维各分维度上，学生的合作能力水平最高，创造力和批判思维能力次之，算法思维和问题解决能力相对较弱。究其原因，随着课程教学改革的不断深入，合作学习逐渐成为学生较为熟悉的学习方式，大大提升了学生的合作能力。同时，现有研究表明，在合作交流中学生往往积极进行头脑风暴，进一步激发了创造思维和批判思维的发展[34]。从认知发展的角度来看，对于普遍年龄在9-13岁的小学中高年级学生而言，其正处于认知发展的具体运算阶段，逻辑思维水平、抽象思维水平初步发展，因此算法思维所涉及的抽象概念，会造成小学生一定的理解困难。此外，目前小学阶段的信息技术课程中仍以技术操作技能学习为主，而对学生思维培养的缺失现象比较严重，从而综合表现出在算法思维和问题解决能力上的弱势。因此，小学生计算思维的发展与培养需要循序渐进的过程与丰富多样的形式.为学生提供合适的环境，让他们用有形的物体和各种趣味任务来发展他们的算法思维技能。通过影响学生的推理、联想、交流和算法思维技能，全面提高计算思维能力。

3.小学阶段在高、中年级水平与性别间，学生计算思维整体能力均不存在显著差异，但在算法思维、问题解决能力、合作能力三个分维度上，小学生群体分别表现出年级水平或性别间的差异。小学生计算思维能力在中、高年级水平与性别间均不存在显著差异的结论，与以往一些研究的结果一致，印证了相比中学阶段，性别、年龄因素的影响力在小学阶段相对减弱的判断[35]。这一发现一方面说明小学中、高年级学生对计算思维能力具有同等的感知度及平等的发展基础，另一方面也说明由年龄增加而获得的认知成熟度增加，并不能直接转化成计算思维能力水平的提升，对小学生进行有针对性的计算思维培训更可能起着决定性的作用。本研究发现，随着年级的提升，小学生算法思维呈现显著下降的趋势。算法思维关注学习者对数据处理流程及数据间关系的把握，在小学阶段这一内容通常属于数学学科范畴。鉴于相关研究已证实数学学习兴趣随年级升高而逐步衰减[36]的趋势，故算法思维呈现下降趋势的原因或与学生数学学科兴趣减弱相关。此外，女生在合作能力和问题解决能力方面得分较男生更突出。该结论与学习科学、通用合作问题解决以及PISA 2015的调查结果均表现一致[37]。因此，教师需要在课堂教学中采用兼顾性别差异的合作教学策略，为培养学生计算思维能力营造良好环境。

4.计算思維能力显著影响小学生数学和语文学业成绩，且其影响存在学科差异。目前研究还较少关注计算思维能力与学生学业成绩的关系。本研究结果表明，计算思维能力越高的小学生，学业成绩越好，即计算思维不仅对数学学科，而且对语文学科的学习同样有促进作用。因此，政府、学校、家庭需要进一步关注这一影响，重视在学校课堂中培养计算思维的必要性。同时，计算思维能力各分维度对不同学科学业成绩的预测作用存在差异。如算法思维、批判思维对数学成绩有较强的预测作用，说明这两类能力是完成数学学习必备的重要能力;而批判思维则对语文学科有较强的预测作用，说明这项能力能够有效促进语言类学科的学习。因此，教师在对学生学科能力培养的过程中，应当对重要的计算思维能力进行有针对性地培养，从而更加有效地促进学业成绩的提高。基于本研究样本，问题解决能力与数学成绩呈显著负相关关系。任友群等人在相关研究中对该问题进行了探讨[38]，认为其原因在于教师在课堂中普遍使用传统的讲授教学法，尽管讲授法能够让学生聚焦于核心学科内容，以提升数学成绩，但却妨碍了学生的主动思考与知识迁移应用，不利于学生问题解决能力的培养。因此，在确保基本教学水平的基础上，应鼓励教师进行多样化的课程开发和实验，注重采用促进学生自主、合作、探究学习的教学方法，实现知识学习与思维能力的共同发展。

（二）研究展望

在合理有效评测的基础上，科学地开展计算思维教育是本研究的初衷。需要指出的是，计算思维作为全球公认的信息时代公民必备能力，是一个高度抽象、结构复杂的多维度概念，难以通过一种方式同时对其整体性与细节性进行全面测评。研究者们建议应系统融合多种相互补充的测评工具，以实现对学生计算思维全方位的理解。因此，后续研究工作中我们将继续深入探究我国小学生计算思维量表与其他计算思维测量工具间的关系，以及该量表在中学群体的适用性等问题。

本研究分析了性别及年级水平对小学生计算思维及其各分维度能力的影响。然而，除上述两个因素外，学生的内部心理变量、先前知识经验、教学环境等都可能对计算思维产生影响，且相关研究目前还较缺乏。因此，后续研究十分有必要基于真实的小学课堂，深入研究计算思维的影响因素和发展趋势，从而更细化地分析出促进学生计算思维发展的教学干预策略，为今后的计算思维培养提供更有力的实证指导。

本研究探索性地讨论了计算思维对小学生数学和语文成绩的影响。显然，确切的影响机制还需要在后续研究中进一步讨论。鉴于采用跨学科教学、统整式教学模式在培养学生计算思维能力的优势[39]。后续研究还需要对不同教学情境中计算思维培养的“质”与“量”做进一步的评估，以便系统探讨计算思维与数学、语文、科学、英语等各科学业成绩的关系。

参考文献：

[1] Darling-Hammond L.A future worthy of teaching for America [J].PhiDelta Kappan，2008，89（10）：730-736.

[2] Wing J M.Computational thinking [J].Communications of theACM，2006，49（3）：33-35.

[3] The New Media ConsortiuⅡLThe NMC/CoSN Horizon Report：2017K-12 Edition [DB/OL].https：//library.educause.edu/-/media/files/library/2017/11/2017hrk12EN.pdf，2020-05-15.

[4]Wing J M_Computational thinking and thinking about computing[J].Philosophical Transachons of the Royal Soeiety A：Mathematical，Physical andEngjneering Sciences2008366（1881）：3717-3725.

[5]周佳伟，工祖浩.科学教育中的计算思维：理论框架与课程设计[J].中国电化教育，2018，（11）：72-78.

[6]中华人民共和国教育部.普通高中课程方案和语文等学科课程标准（2017年版）[DB/OL].http：//www.moe.gov.cn/s rcsite/A26/s8 001/2018 01/t2 018 0115_3 24647.html，2019-10-08.

[7]孙立会.聚焦思维素养的儿童编程教育：概念、理路与目标[J].中国电化教育，2019，（7）：22-30.

[8] Denning P J.Beyond computational thinking [J].Communications of theACM，2009，52（6）：28-30.

[9]周宏仁.信息化：从计算机科学到计算科学[J].中国科学院院刊，2016，31（6）：591-598.

[10] Weintrop D，Beheshti E，et al.Defining computational thinking formathematics and science classrooms [J].Journal of Science Educationand Technology，2016，25 （1）：127-147.

[11] Syslo M M，Kwiatkowska A B.Informatics for all high school students：acomputational thinking approach[A].International Conference onInformatics in Schools：Situation，Evolution，and Perspectives [C].Berlin，Heidelherg：Springer press，2013.43 -56.