镎(IV)、镅(III)、锔(III)的AMBER力场参数化及评估

刘子义，夏苗仁，柴之芳，王东琪

1中国科学院高能物理研究所多学科中心, 北京 100049

2中国科学院大学化学学院, 北京 100049

3苏州大学放射医学与辐射防护国家重点实验室, 苏州大学放射医学与防护学院, 江苏 苏州 215123

1 引言

近年来，随着计算能力的迅速提高，使用计算机模拟化学微观体系并探究作用机制的方法逐渐成为化学研究的主要手段之一。在此方法中，合理地描述粒子间的相互作用是确保模拟结果可靠的关键。为了改进和完善对粒子间相互作用的描述，在过去的几十年里，发展了多种理论模型，主要可分为两类：(a)基于电子运动规律的量子力学描述；(b)基于分子力场的经典力学描述。其中，量子力学方法通过求解薛定谔方程获得电子的运动规律，进而得出分子体系的性质，与实验值有较好的吻合，但由于算法等限制，计算量大，以目前的计算能力难以处理复杂体系。分子力场的描述忽略了电子自由度，用经典力学的经验方程取代迭代算法，将原子作为点模型处理，有效地提高了计算效率，可以处理数百万原子的体系。在分子力场的描述中，粒子间的相互作用分解为键相互作用和非键相互作用。其中，键相互作用包括键伸缩、角弯曲、二面角扭转等，非键相互作用包括库伦作用和范德华作用。根据模拟体系和科学目标的侧重点不同，相互作用的函数表达式不同，发展出不同版本的力场。目前常用的力场有AMBER1、GROMOS2及CHARMM3等。

研究锕系元素(An)在水溶液中的行为对于理解锕系元素的迁移、放射性废物处置及核燃料的分离过程有着至关重要的作用。特别是针对不断增加的核燃料废料的科学挑战，使用离子交换、溶剂萃取、电沉积等方法从混合物中分离出放射性核素(如U、Np、Pu、Am等)，都需要深入了解锕系元素在水溶液中的化学行为。通常，在水溶液及生物体系中，Th、U、Np、Pu等元素以四价单原子离子形式存在，其中U还能以铀酰离子(UO22+)形式存在，而Am和Cm一般以三价单原子离子形式存在。由于锕系元素具有高放射性和化学毒性，在实验上研究这些金属离子的水溶液化学行为较为困难。而理论化学中的量子力学描述方法由于昂贵的计算成本，只能关注这些元素周围第一配位层水分子的配位行为，同时，也很难提供动力学的信息。基于分子力场的模拟是一种可替代的方案4，而锕系金属的力场参数是描述锕系溶液行为的关键。

由于锕系元素电子结构的复杂性，如高角动量、多组态、极化效应、相对论效应、旋轨耦合等，导致锕系元素具有复杂的化学行为，因此，相比于碳、氢、氧、氮等主族元素，锕系元素力场参数的拟合更具有挑战性，需要考虑多方面的影响，如锕系元素的价态、种态和化学环境等5。从上个世纪90年代以来，多个课题组致力于锕系元素特定氧化态下力场参数的开发，包括有Wipff课题组报道的UO22+在水溶液中的AMBER力场参数6,7；Maginn课题组根据量子化学计算出的势能面拟合出五价、六价锕酰离子(AnO2+/2+)的AMBER力场参数8；Merz等在AMBER力场框架下根据An―Ow的键长和An的溶剂化自由能拟合出了Th4+、U4+、Pu4+的12-6及12-6-4势的力场参数9,10等。Am3+和Cm3+在极化力场中有相应的参数报道，如Gagliardi等11报道的Cm3+的NEMO力场参数、Spezia等12报道的Am3+、Cm3+的类Car-Parrinello力场参数等。这些参数能够较好地重现实验结果，但受限于较大的计算量、力场参数较少且各版本极化力场之间的不可移植性等因素，制约了极化力场的应用，有关锕系溶液动力学在力场水平上的研究仍以非极化力场为主。另外，目前Np4+、Am3+、Cm3+的非极化力场尚未报道。

本项工作旨在补充对于锕系关键离子Np4+、Am3+、Cm3+的AMBER力场参数，通过对比文献报道的相关理论与实验结果，评估参数的可靠性，进而结合文献报道10的Th4+、U4+、Pu4+参数，系统研究这几种重要的锕系离子在水溶液中的动力学。

2 研究方法

2.1 参数化

通常情况下，对于单原子离子，粒子间的相互作用只包含非键相互作用，即静电相互作用和范德华相互作用13，其中，在非极化力场框架下，静电相互作用采取固定点电荷模型的库伦公式，范德华相互作用一般采取12-6 Lennard-Jones (LJ)势。在AMBER力场中，其函数形式如下：

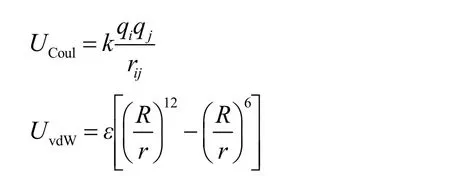
由上式可知，静电作用取决于原子所带电荷，对于单原子离子，原子电荷与其价态相等。LJ参数中的ε和R分别代表两个原子之间LJ关系中的势阱深度及对应的原子间距，是准确描述单原子金属离子范德华相互作用的关键。

2.1.1R和ε的关系

1924年，Lennard-Jones 提出LJ势14的初衷是准确描述惰性气体中原子之间的相互作用，其中r-12项表示由于近距离分子轨道重叠而引起的泡利斥力，r-6项表示色散力产生的长程分子间的吸引力。之后，这种描述方法被证明也能够很好地描述中性原子和分子之间的范德华相互作用。1964年，Stokes运用quantum mechanical scaling principle(QMSP)方法15计算了与惰性气体原子具有相同电子结构的金属离子的范德华半径。2013年，Merz等9在一项二价金属离子范德华参数优化工作中依照此范德华半径数值，通过在参数空间内寻找最优参数，证实单原子金属离子的R和ε的关系与惰性气体一致。同时提出惰性气体的R和ε的关系满足：

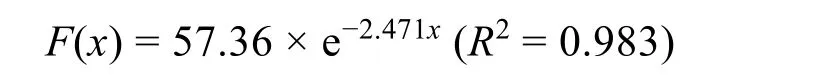
其中，F(x)代表-log(ε)，x代表R/2。

基于此关系，单原子离子的LJ势UvdW与R、ε的关系，可以转换为UvdW仅与R的关系。

2.1.2 R和IOD的关系

由上可知，单原子金属离子的Uvdw与R值是一一对应的。在水溶液中UvdW值对应于M―Ow原子对的距离(ion-oxygen distance，IOD)，即在水溶液动力学过程中，相同价态的单原子金属离子的R值与IOD值有一一对应关系。根据Merz等10报道的常见M3+/4+的力场参数及特定价态的单原子金属离子在水溶液动力学模拟中R和IOD的变化趋势，可得M3+/4+的IOD和R/2存在以下关系(图1)：

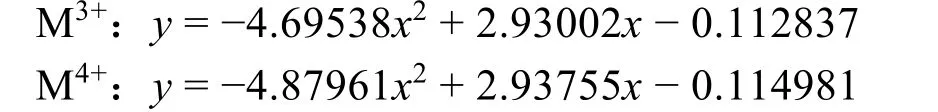
本文选取SPC/E作为水模型，根据各锕系离子的IOD值得到其R/2值。

2.2 IOD值的选取

依照图1，对于Np4+、Am3+、Cm3+离子，只要确定合适的An―Ow的键长(IOD)，就可得出该离子的LJ参数。三种离子的IOD值确定方法如下：

(1) Np4+：有多项实验研究报道了Np的水溶液化学性质，包括其热力学16、电化学17、光谱学18及配合物结构19等。根据Allen等20对Cl-浓度极低的水溶液环境中Np4+的水合物的扩展X射线吸收精细结构(EXAFS)光谱的解析，Np4+与Ow的配位键长为0.240 nm，配位数(CN)为11.2。另一项工作21解析了Np4+在1 mol·L-1HClO4溶液中的EXAFS谱，得到相同的配位键长。

由于相关报道中22各项工作溶液离子环境的不同，Np4+―Ow键的键长测量在0.239-0.240 nm之间，稀溶液中Np4+―Ow的键长多为0.240 nm。由于稀溶液中IOD值受反离子的影响最小，本文选取Np4+在水溶液中的IOD值为0.240 nm。

(2) Am3+：根据Stumpf等23对水溶液中的Am3+的EXAFS研究，得到Am3+―Ow的键长在0.247-0.249 nm，配位数为8.3，这与Allen等24在0.25 mol·L-1HCl溶液中得到的Am3+―Ow键长(0.248 nm)一致。本文选取0.248 nm作为Am3+在水溶液中的IOD值。

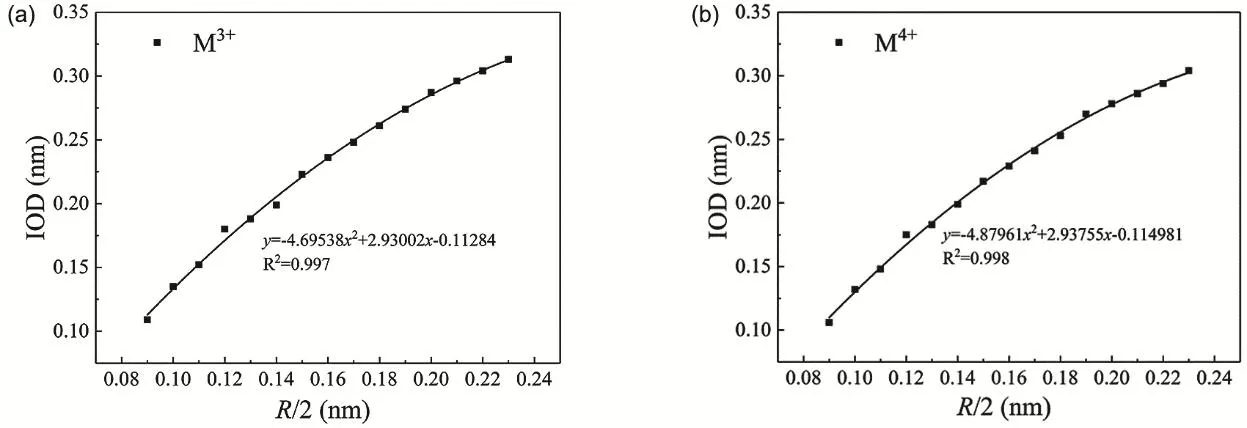
图1 SPC/E水环境中R/2和IOD之间关系的多项式方程10Fig. 1 IOD as a function of R/2 in water (SPC/E) 10.(a) M3+; (b) M4+.

(3) Cm3+：根据时间分辨激光荧光光谱研究25，Cm3+的高氯酸盐在水溶液中存在8配位水合物和9配位水合物物种的平衡，且以9配位为主；另外一项高能X-射线与EXAFS联用研究26表明1 mol·L-1HClO4溶液中，Cm3+的水分子配位数为8.8。两项工作都表明Cm3+外层水分子配位数接近于9。Allen等24对Cm3+溶液的EXAFS研究报道Cm3+―Ow键长为0.245-0.246 nm，在较低的离子强度下测得IOD为0.245 nm，CN = 10.2；而在较高的离子强度下IOD为0.246 nm，CN = 9.3。为了尽可能准确模拟Cm3+的外层水分子配位数，本文选取0.246 nm作为Cm3+的IOD值。

基于上述的各金属离子的IOD值，优化得到相应的LJ参数(表1)。采用该套参数计算得到的金属离子与SPC/E水分子模型相互作用的Lennard-Jones势函数曲线如图2所示。

2.3 计算方法

本文的分子动力学工作采用AmberTools1627程序完成，An3+/4+的范德华参数采用表1中的数值。水分子采用SPC/E模型28处理，Cl-的参数取自文献29，CO32-、NO3-的力场参数使用antechamber程序30拟合，其电荷采用由半经验量化程序sqm工具生成的AM1-bcc电荷31,32。动力学过程中的非键相互作用截断距离为1 nm，长程静电相互作用采用smooth PME的计算方法33。H原子与重原子之间的化学键采用LINCS限制算法34加以约束以保证1 fs时间步长的合理性。所有的模拟体系均包含约1500个水分子，分布在大小约2.9 nm × 2.9 nm × 2.9 nm的正方体盒中。各搭建好的模型体系经过以下四个阶段获取可用于分析的平衡动力学数据：(1)初始构型能量最小化；(2)升温到目标温度298 K：从250 K分两阶段至298 K，总时长100 ps；(3)预平衡过程：NPT系综，T= 298 K，P= 1.013 ×105Pa，总时长500 ps；(4)采样：在298 K、1.013 ×105Pa的NPT系综下，采样20 ns用于分析。温控采用Berendsen弱耦合技术35，其中τT= 0.5 ps；压力控制采用Berendsen压浴方法，其中τP= 2 ps。

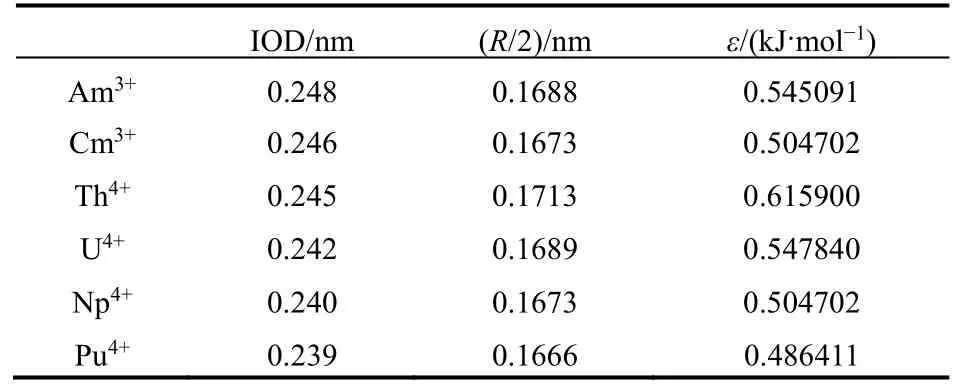
表1 几种三价(Am3+、Cm3+)和四价(Th4+、U4+、Np4+、Pu4+) a锕系离子的IOD及拟合的LJ势参数R/2和εTable 1 The IOD and LJ parameters (R/2 and ε) of several tri- (Am3+, Cm3+) and tetra-valent (Th4+, U4+, Np4+,Pu4+) a actinide cations.

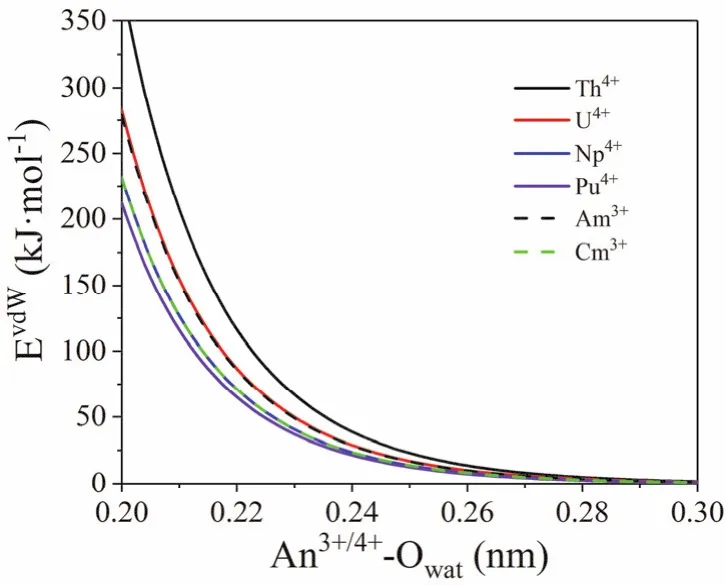
图2 根据表1中的LJ参数得出的An3+/4+-水的Lennard-Jones势函数曲线Fig. 2 The Lennard-Jones potentials of An3+/4+-Ow using the parameters in Table 1.

金属离子溶剂化自由能的计算采用自由能微扰(Free Energy Perturbation，FEP)的方法，将金属离子从气相微扰到水溶液相，每个微扰状态由λvdW和λcoul两个变量控制，分别表示金属与水环境的范德华、库伦相互作用微扰系数，每个微扰变量从0到1的步长为0.05，对应每个金属离子的微扰过程共有41个窗口，每个窗口在NPT系综下采样1 ns，最后基于每个窗口间的交叉能量关系，采用Bennett acceptance ratio方法36计算出两个微扰窗口间的自由能差异：

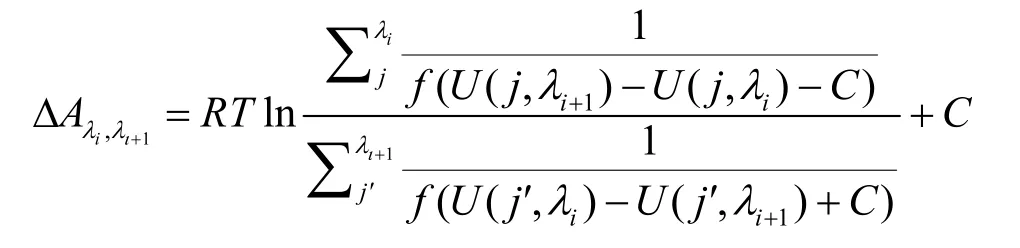
其中f是气体常数R和温度T的函数：

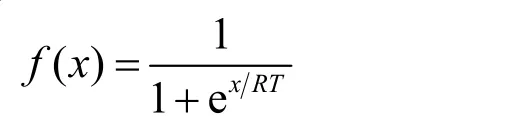
金属第一溶剂化层水分子的平均驻留时间的计算首先根据下式计算相关函数R(t)37：

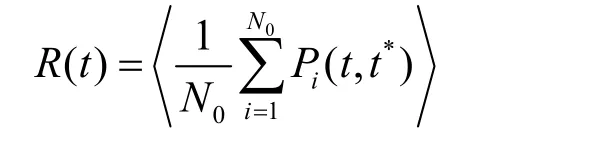
其中N0为时刻离子第一溶剂化层的总水分子数，Pi(t,t*)为阶梯函数，当t时刻第i个水分子与0时刻第i个水分子相关，则为1。当且仅当第i个水分子同时在t和0时刻在第一溶剂化层，同时不能连续脱离第一溶剂化层超过t*时间长度，Pi(t,t*)才为1，否则为0。计算中使用的t*为10 ps，第一溶剂化层的截断距离为0.282 nm。然后使用如下的公式计算驻留时间τ：

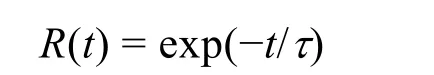
当R= e-1≈ 0.3679时，τ=t，即该值为驻留时间。

配位层水分子与体相水的交换速率与其反应活化能的关系用Eyring方程38表示，其形式如下：

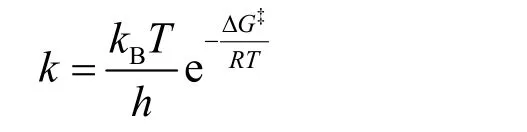
其中kB为波尔兹曼常数(1.381 × 10-23J·K-1)，T为绝对温度，h为普朗克常数，k为反应的速率，ΔG为反应的活化自由能。

3 结果与讨论

3.1 An3+/4+水溶液动力学

3.1.1 An3+/4+溶剂化结构

首先计算了Th4+、U4+、Np4+、Pu4+、Am3+、Cm3+等锕系离子与水中氧原子Ow之间的径向分布函数(RDF)及其积分值以分析其溶剂化结构，并与文献值10,12,20,24,39-50进行对比，详见图3和表2。可以看出六种金属都有明显的第一、二水配位层，其第一配位层水的RDF峰值分别在0.243 nm (Th4+)、0.239 nm (U4+)、0.239 nm (Np4+)、0.237 nm (Pu4+)、0.248 nm (Am3+)、0.246 nm (Cm3+) (表2，图3)，除了Th4+的配位数为10外其余都为9，这与参数拟合所用的IOD值20,24吻合。同时，我们的模拟结果也与已报道的相关理论工作吻合，如Yang和Bursten39采用量子化学的方法计算得出Cm3+与第一配位层水的配位键长为0.248 nm；Gagliardi等11采用NEMO力场在300 K下模拟得到的Cm3+―Ow的键长为0.255 nm，高于Yang等39、EXAFS测量值24及本套力场模拟值；Spezia等12采用极化力场得到Am3+―Ow和Cm3+―Ow的键长分别为0.248和0.245 nm，配位数均为9，与本文的非极化力场模拟结果一致；Rode等40采用量子力学电荷场(QMCF)动力学报道第一配位层U4+―Ow的键长为0.245 nm，略高于实验值41(0.242 nm)及本文计算值；Jong等42使用CPMD方法计算得到的Pu4+―Ow的键长为0.247 nm，高于实验值43(0.239 nm)，配位数(水分子)为9；Macedo等44采用BP86泛函方法计算出在COSMO溶剂模型下，Np4+、Th4+的水合物中金属离子的配位数为9时，Th4+―Ow和Np4+―Ow的距离分别为0.247和0.239 nm，与本项工作吻合。

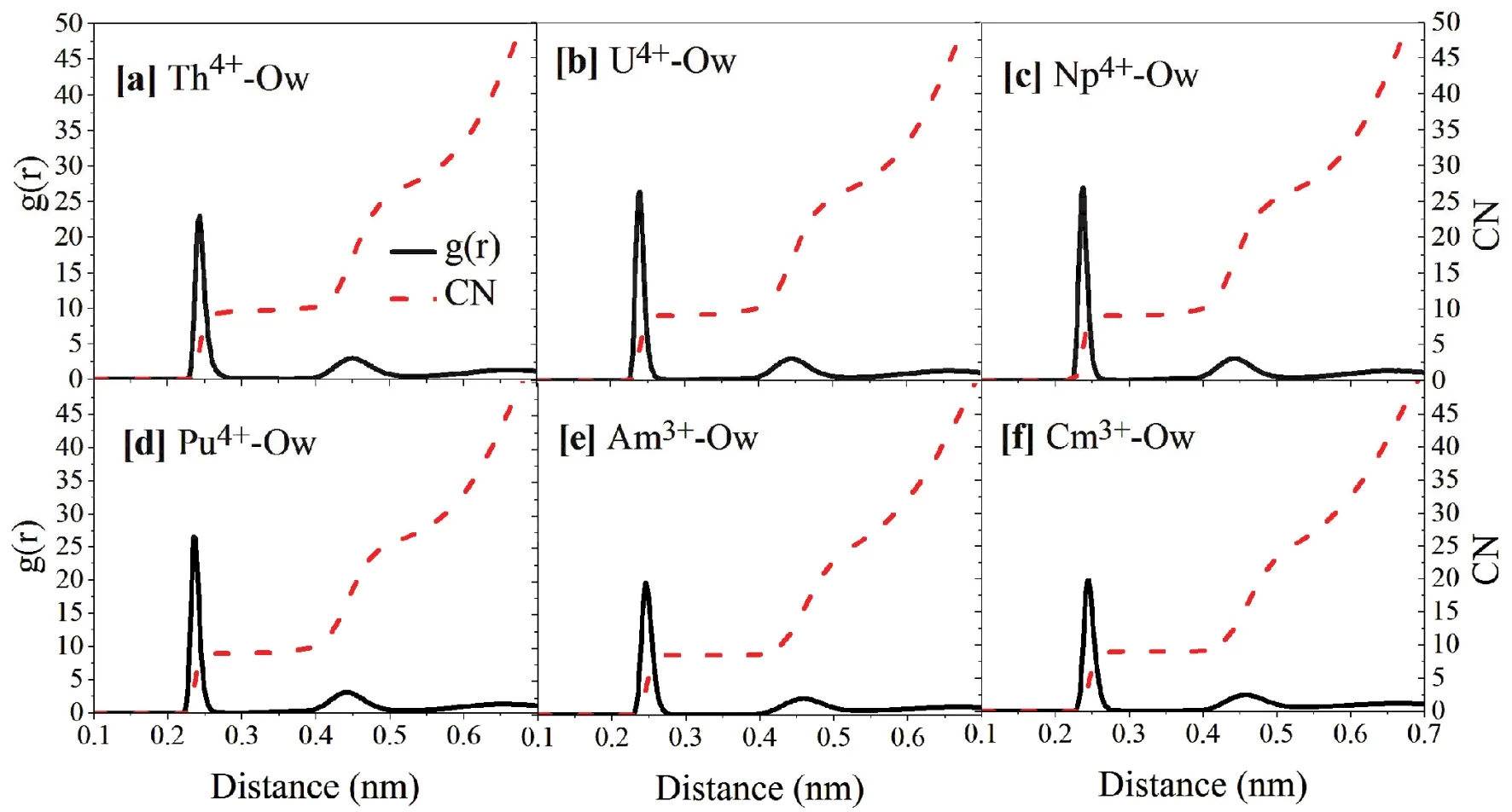
图3 20 ns模拟过程的An4+/3+周围水分子氧原子的径向分布函数(黑色实线)及其积分(红色虚线)Fig.3 Radial distribution function (solid black line) and its integral (dashed red line) of water molecules around An4+/3+ during 20 ns MD simulations(a) Th4+, (b) U4+, (c) Np4+, (d) Pu4+ (e) Am3+, (f) Cm3+. Color online.

实验报道Th4+和Np4+的配位数分别是9-10和8-1020，且不同配位数的配位结构间能量差很小45。Yang等报道46的采用B3LYP泛函的[Th·9H2O]4+·3H2O与[Th·10H2O]4+·2H2O水溶液结合能仅差1.256 kJ·mol-1, 表明了9与10配位结构可以在溶液中共存，本项工作在力场水平上模拟出了一致的结果。

第二配位层的水分子受金属的影响相对较弱。由于有关Am3+的第二水分子配位层的配位距离报道较少，而U4+、Np4+、Pu4+则缺乏相关的实验数据，我们主要讨论Cm3+的第二配位层结构。根据对锕系离子周围水分子径向分布函数(RDF)的分析(表2，图3)，Cm3+与第二水分子层水的Cm3+―Ow键长为0.456 nm，这较接近于Spezia等12极化力场下的动力学结果(0.462 nm)。第二水分子层配位数为16，与Atta-Fynn等47的AIMD (15.8)、3-body MD (17.4)结果接近，小于Spezia等12(20.8)、Yang和Bursten等39(21)的模拟结果，说明第二水分子层的溶剂结构对于模拟体系、模拟方法的依赖性较高。

3.1.2 金属离子配位层的水分子的运动性质

由上述金属离子的溶剂化结构可知，An4+比An3+具有更紧凑的溶剂结构，表明An4+与溶剂的相互作用更强(图4)。这种较强的相互作用不仅表现为更短的An―Ow距离，而且对金属周围水分子的空间排序、平动及转动性质都带来较大的影响。

An3+/4+第一配位层的水分子的空间取向高度有序，其偶极矩的朝向与An―Ow键轴方向总是保持一致。图5表明，在1 nm的非键相互作用截断距离内，An3+/An4+对外层水分子有序性都有影响，并随着距离的增大水分子的有序性减弱。An4+对第一、二层水分子的有序性影响要强于An3+，表现在更小的偶极矩与An―Ow方向的夹角(第一配位层水分子：0°-33°vs0°-45°，第二配位层水分子：0°-70°vs0°-90°)。

金属外围水分子的高度有序给水分子的平动、转动性质带来了影响。由表3可得，在同样九配位的An4+/An3+体系中，An4+前两水分子层的扩散速度要慢于An3+体系，同时该部分水分子的转动弛豫时间也要慢于An3+体系。这归因于An4+与外围水分子具有更强的静电相互作用(图4)。

3.1.3 第一配位层水分子的驻留时间与交换活化能

在20 ns的分子动力学模拟中，Am3+、Cm3+的第一配位层水分子较少发生与第二层的水分子进行交换，说明Am3+、Cm3+对第一配位层的水有较强的束缚能力，通过计算相关函数得出Am3+的第一层水驻留时间为18.4 ns，而对于Cm3+，该值无法在20 ns的时长采样下准确测得，但根据前20 ns的轨迹分析，估算Cm3+的第一层水驻留时间约为34 ns。这与Dognon等51、Spezia等12的An3+在数纳秒的溶液动力学内都未观测到第一层水与第二层水的交换现象吻合。

对比之下，四价锕系离子的第一配位层的水分子在动力学过程中表现地比较活跃，并且随原子序数的增大其平均驻留时间也增大。计算得到的An4+的驻留时间分别为0.19 (Th4+), 0.27 (U4+),0.5 (Np4+)和0.83 (Pu4+) ns。根据相关实验报道52数据换算得到的Th4+与U4+的驻留时间分别是＜ 20 ns和180 ns。因此相对于实验值，分子模拟过程的水分子交换过快，但是其变化趋势是一致的。对于Np4+和Pu4+体系，文献中鲜有相关的实验和理论报道。从上述分子模拟的结果看，对于相同价态的An3+/4+，随着原子序数的增大，对水分子的束缚能力增强，与An―Ow的键长值顺序一致。

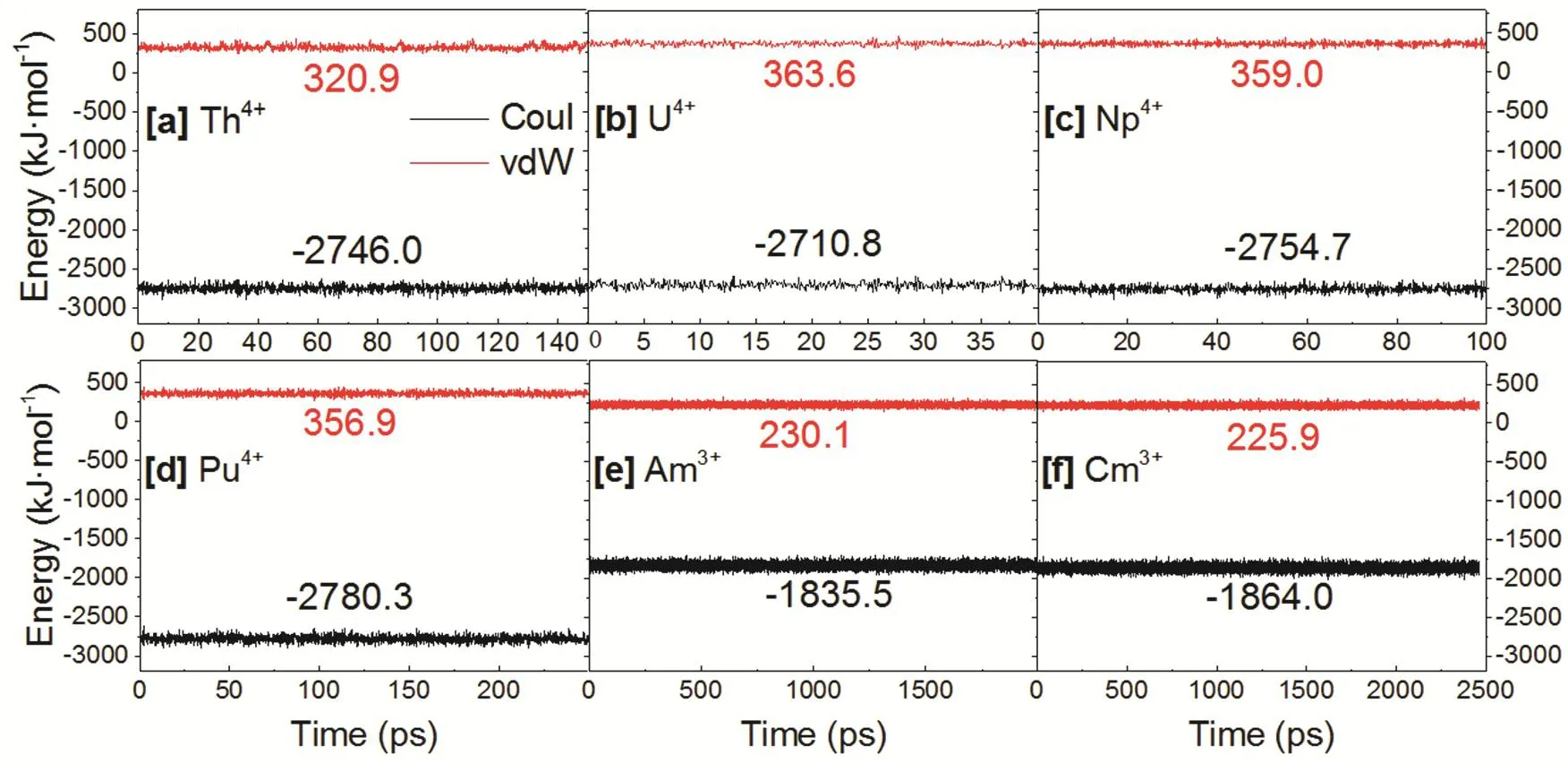
图4 An4+/An3+与轨迹中稳定的第一水分子层间的相互作用能分解Fig. 4 The decomposition of the interaction energy between An4+/An3+ and the water molecules in the first coordination shell during MD simulations.(a) Th4+, (b) U4+, (c) Np4+, (d) Pu4+, (e) Am3+, (f) Cm3+.

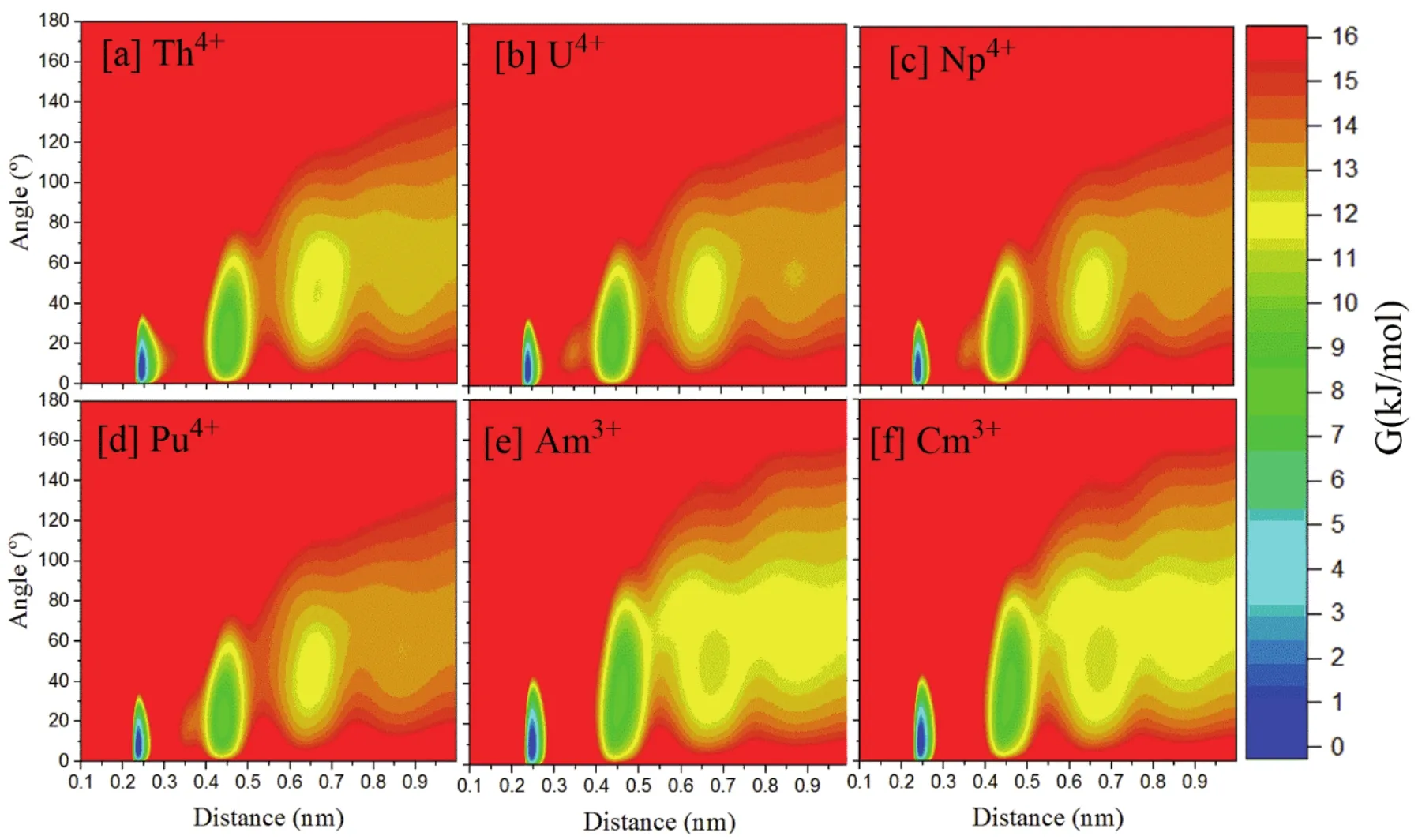
图5 在20 ns的动力学中An-Ow矢量与水分子偶极矩的夹角与An―Ow距离的关系，及构型间的Gibbs自由能差异(kJ·mol-1)Fig. 5 The population of the angle between An-Ow vector and water dipole moment as a function of the An―Ow distance,the populations were normalized and shown in the form of relative Gibbs free energy (kJ·mol-1).

由于An4+外围水分子高度有序，可以认为熵效应并不是影响An4+第一水分子层较短驻留时间的主要原因。通过分析溶剂间的相互作用，发现An4+紧凑的溶剂化结构会带来更多溶剂间的范德华互斥和静电互斥作用(图6)，比An3+溶剂间的能量高约84-155 kJ·mol-1，这促进了第一水分子层向第二水分子层的转移。

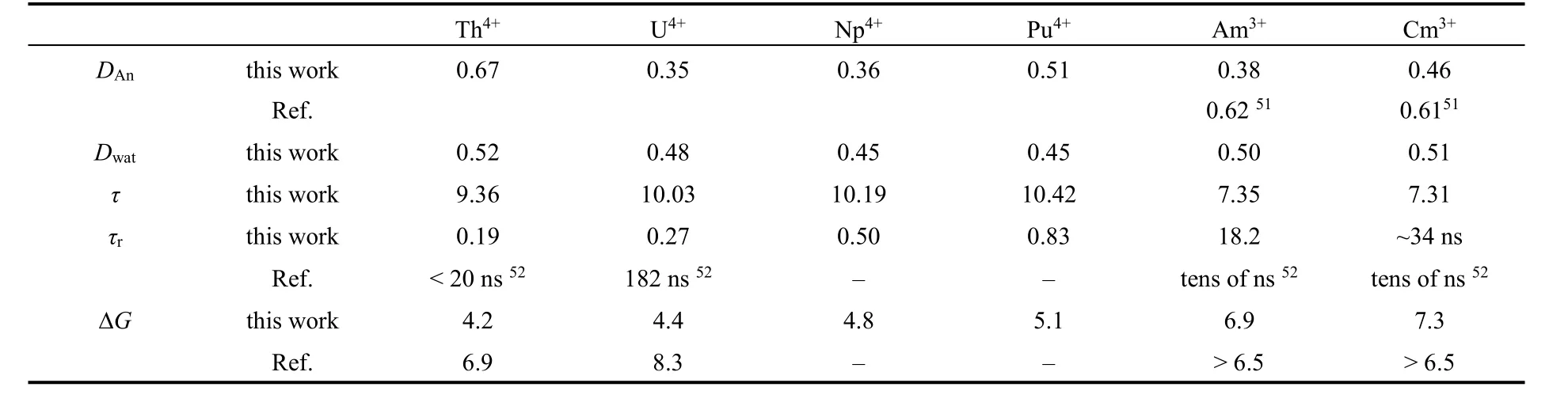
表3 金属离子扩散系数(DAn，10-5 cm2·s-1)，第一、二配位层水分子的扩散系数(Dwat，10-5 cm2·s-1)和转动弛豫时间(τ，ps)，第一配位层水分子的平均驻留时间(τr，ns)和根据 Eyring方程 38计算的活化能(ΔG≠，kJ·mol-1)Table 3 The diffusion coefficients of An4+/An3+ (DAn, 0-5 cm2·s-1), the diffusion coefficients (Dwat, 10-5 cm2·s-1) and rotational correlation time (τ, ps) of water in the first and second hydration shells, the mean residence time (τr, ns) of water in the first hydration shell and corresponding activation energies (ΔG≠, kJ·mol-1) calculated by Eyring equation 38.

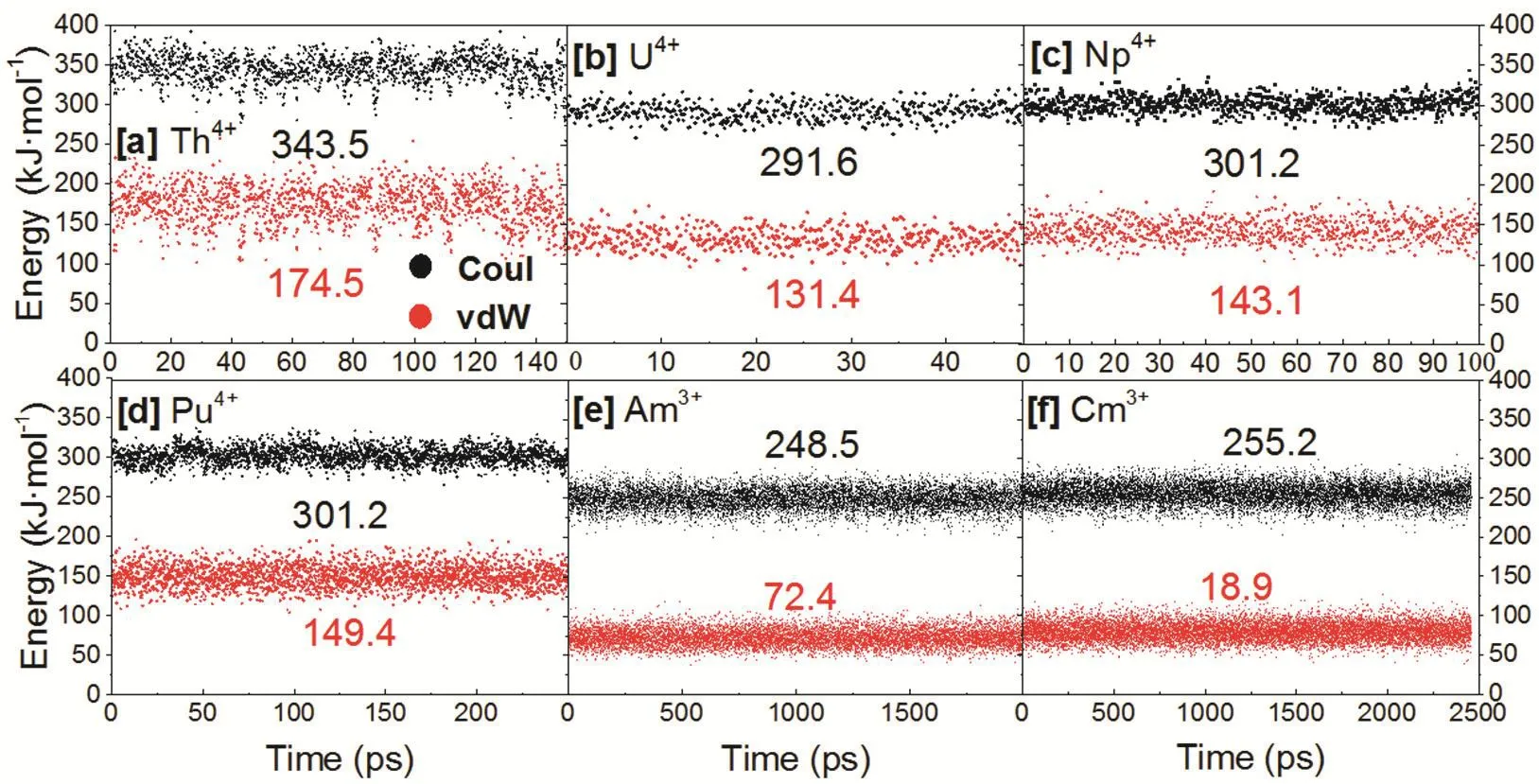
图6 动力学过程中稳定水合结构的连续轨迹中第一配位层水分子内部相互作用的能量分解为静电相互作用(黑色)和范德华相互作用(红色)Fig. 6 The energy decomposition of interactions between intra-cluster water molecules in the first hydration shell: electrostatic (black) and vdW (red) interactions. Only continuous trajectory of stable hydrated structures without water exchange were analyzed.Average values of these energy components (kJ·mol-1) are shown. Color online.

3.1.4 配合结构立体构型

根据对轨迹的分析，在298 K，除Th4+外的五种锕系金属离子的配位数都保持为9。从立体化学的角度，金属及其外层的9个配位原子可形成包括单帽四方反棱柱体(capped square antiprism，CSAP)和三帽三角棱柱体(tricapped trigonal prism，TCTP)的立体结构53。

根据对动力学模拟轨迹的分析(图7)，[ThIV(H2O)10]4+的第一配位层立体化学结构为双帽四方反棱柱体(bicapped square antiprism，BCSAP)；而[UIV(H2O)9]4+，[NpIV(H2O)9]4+，[PuIV(H2O)9]4+采取的立体化学构型为CSAP，与Yang等46报道的采用量子化学的方法证明九配位的[ThIV(H2O)9]4+的CSAP构型比TCTP构型更稳定的结论相似。Am3+的相关报道较少，但一般认为An3+与Ln3+水合物的立体结构相似，均采取TCTP构型。一项An3+/Ln3+的配位化学研究54提及[AmIII(H2O)9][CF3SO3]3中为TCTP构型，但我们的纯水溶液动力学中观察到Am3+保持CSAP构型，这两者的差异可能是因为单晶X-ray的测量方法中加入的[CF3SO3]-反离子分布在第二配位层，对第一配位层水分子的排列产生的影响导致的55。[CmIII(H2O)9]3+为TCTP构型，与Yang和Bursten等39运用量子化学方法得出相同的构型，表明该套参数的动力学模拟可以较好描述金属第一配位原子层的立体化学结构。

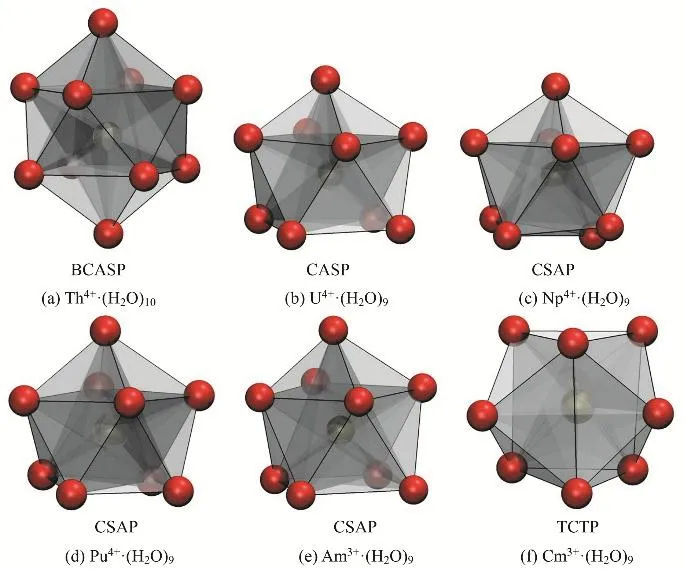
图7 MD捕捉到的An4+/3+的水合物的优势立体几何结构Fig. 7 The dominant conformations of the hydrated An4+/3+ during MD sampling.(a) Th4+, (b) U4+, (c) Np4+, (d) Pu4+, (e) Am3+, (f) Cm3+.

3.1.5 溶剂化自由能(HFE)

通过运用自由能微扰方法，计算得出六种锕系金属离子在该套参数描述下的溶剂化自由能ΔG(FEP)。但由于非极化力场函数式中未引入极化项，忽略了诱导偶极作用等相互作用，使用FEP算出的自由能往往会低估溶剂化自由能13。Merz等29对比一系列M3+与M4+的非极化力场的IOD值参数计算出的自由能与实验值比较，总结出在非极化力场下运用FEP的方法，对于三价单原子金属离子，往往会低估约9%的自由能；对于四价单原子金属离子，会低估约16%的自由能13。我们依据此结论，对ΔG(FEP)进行校正，得出校正后的自由能ΔG(CORR)，见表4，并与文献值进行对比56-59。

根据计算结果，Np4+和Pu4+的溶剂化自由能最大，Cm3+比Am3+的溶剂化自由能略高，这与文献报道的结果一致，表明本项工作拟合的An3+/An4+参数能够定性描述An3+/An4+与水的相互作用强弱。

从结果也可看出，随着原子序数的升高，相同价态的An3+/4+的溶剂化效应增强。这主要是由于随着原子序数的增大，An―Ow之间的斥力减小(图2)，有助于An与水的相互作用。相比于An3+，四价离子较高的溶剂化自由能得益于较大的静电相互作用的贡献(图8)。

3.2 An3+/4+与Cl-、NO3-、CO32-的溶液动力学

在镧锕分离及其分析过程，限于实验条件或测量技术，溶液当中会伴随着反离子的存在，如Cl-、NO3-、CO32-等，这些无机阴离子会影响液-液萃取平衡及分析测量的结果，因此有必要研究这些无机阴离子与锕系金属离子共存体系的溶液动力学。在本项工作的模拟体系中，为了探究金属离子与该类无机阴离子的特征配位化学行为，金属离子与无机阴离子均放置1个，以简化环境因素的影响，分析结果与文献值进行对比20,21,24,60-69。

Cl-在锕系单原子离子测量方面是一种常见的反离子，在之前Np4+、Am3+、Cm3+的相关EXAFS工作20,24中给出了不同Cl-浓度下An3+/4+―Cl的键长，我们的模拟结果与实验值有较好吻合(表5)。An3+/4+与Cl-的RDF结果(图S1，见Supporting Information)表明Cl-与Cm3+、Th4+表现出较弱的相互作用，在动力学过程中Cl-在前4配位层之间不断交换，尤其是Cm3+，在2-3配位层的时间长于停留在第一配位层的时间，表明了Cm3+―Cl-弱于Cm3+―H2O的相互作用。其他四种金属离子均可以将Cl-束缚在第一配位层，且An4+对Cl-有较短的配位键长，其作用力要强于An3+。Seminario等60运用DFT的方法计算了10配位的[ThCl3(H2O)7]+配合物在溶剂环境下Th4+―Cl的键长为0.272 nm，在同样条件下8配位的PuCl4(H2O)4中Pu4+―Cl的配位键长为0.262 nm，与本项工作的动力学模拟结果误差在±0.002 nm。而U4+与Cl-在水溶液配位结构的表征工作较少，根据一项1200 K高温下UCl4-NaCl熔盐体系的第一性原理动力学模拟(AIMD)的工作61，U4+―Cl的距离为0.263 nm。整体来看，相同价态下，An3+/4+与Cl-的相互作用随着原子序数的升高而增强。

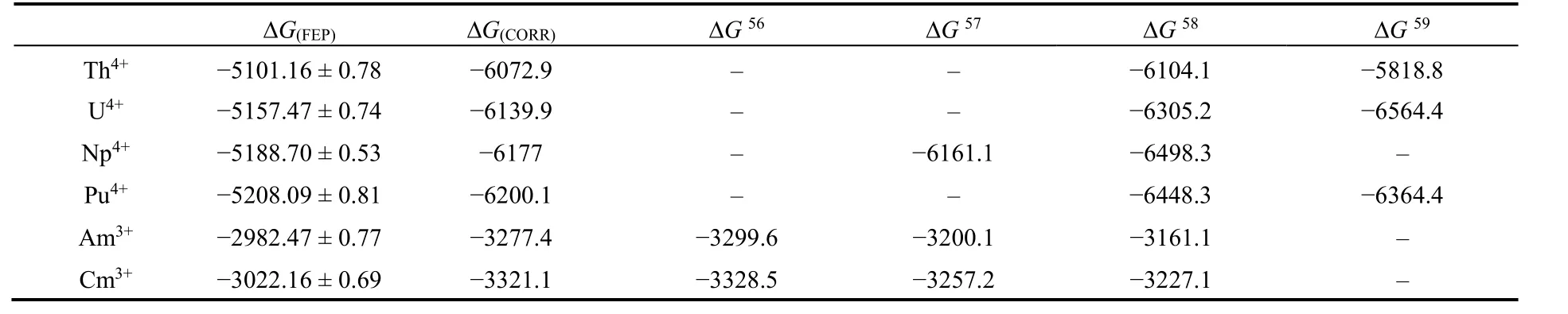
表4 An3+/4+的溶剂化自由能(kJ·mol-1)Table 4 The calculated hydration free energy (HFE) of An3+/4+ (kJ·mol-1).

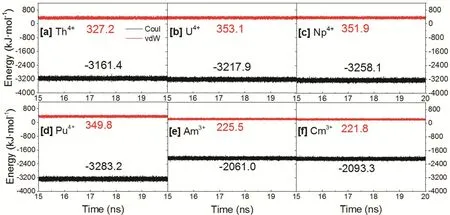
图8 轨迹最后5 ns的金属与水相互作用的能量分解：静电相互作用(黑色)和范德华相互作用(红色)Fig. 8 The energy decomposition of non-bonded interaction into electrostatic (black) and vdW (red) interactions during the last 5 ns of production run.Average energies (kJ·mol-1) are showed. Color online.

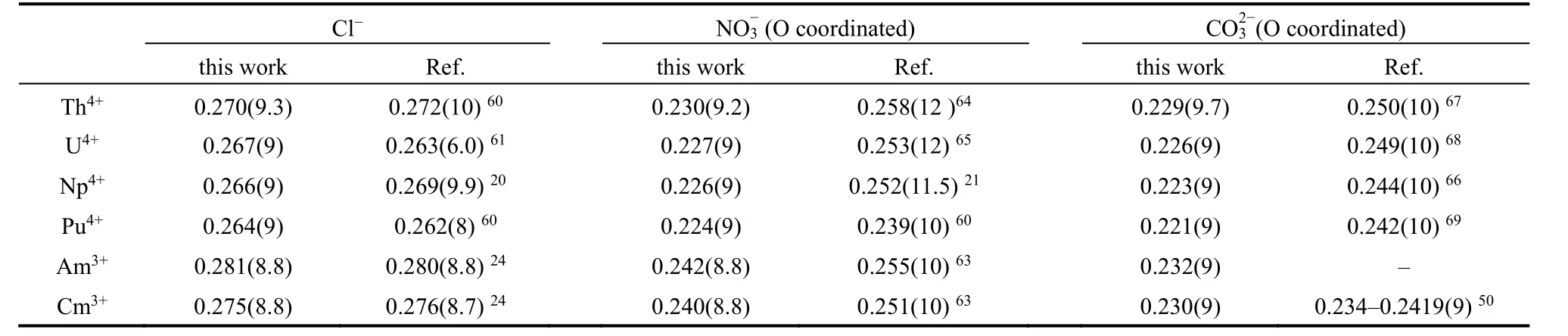
表5 根据基于20 ns轨迹的RDF计算的An3+/4+与Cl-、NO-3、CO23-配位原子的配位键长Table 5 The coordination bond distance (nm) between actinide ion and coordinating atoms of Cl-, NO-3, and CO23- derived from calculated RDF over the 20 ns production run.

硝酸根离子在镧锕分离的萃取过程当中经常出现。在水溶液中，NO3-的配位能力较弱，我们的模拟结果表明六种金属离子在20 ns的采样过程中始终保持着第一配位层的单齿配位。Guibaud等62利用伞形采样的方法计算了NO3-与镧系金属Nd3+和Dy3+的单配位与双配位的能量，发现硝酸根在水溶液中从单配位到双配位需要跨越较大能垒，并且双配位模式不稳定，这在我们的模拟中也有所体现。从模拟的平均键长，硝酸根的配位氧原子(ON)与 An4+的 配 位 键 (An4+―ON)的 键 长 较Am3+/Cm3+―ON的键长短约0.010-0.018 nm。根据密度泛函理论(BP/SVP)研究63，在An(NO3)3·5(H2O)的三价锕系配合物中，2个NO3-是双齿配位，一个NO3-是单齿配位时，总配位数为10，Am3+与其单齿配位的O的键长为0.255 nm，Cm的相应键长为0.251 nm。而对Np4+的HNO3水溶液的EXAFS光谱研究21测得在5.0 mol·L-1HNO3水溶液中，与Np4+配位的氧原子中有约4.5个来自硝酸根，另有7个水分子，配位数为11.5，Np4+和硝酸根配位O原子的配位距离为0.252 nm，这比我们的模拟结果略高，可能是由于研究体系的硝酸根数量、配位模式及金属总的配位数等差异导致。通常情况下，金属的高配位数会弱化配位键而致使配位键增长。另外两项工作64,65分别表征了[Th(NO3)6]2-和[U(NO3)6]2-的晶体结构，NO3-均采用κ2的配位模式，由于金属的高配位数12，其An4+―ON的距离大于我们的水溶液模拟结果。整体来看，同样价态下，随着原子序数的增高，An―ON的配位距离变短。

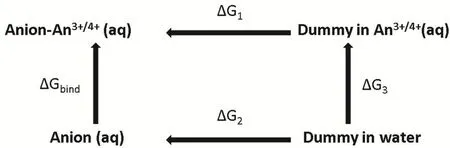
图9 计算 An3+/4+与 Cl-、NO-3、结合自由能所采用的热力学循环示意图Fig. 9 The schematic of thermodynamic cycle used for calculating binding energy between metal ions and anion.

表6 热力学循环计算过程中Cl-、、溶剂化能ΔG2及其与An3+/4+的复合化能ΔG1、结合自由能ΔGbind (单位：kJ·mol-1)Table 6 The anion’s complexation free energy ΔG1 and binding free energy ΔGbind (in kJ·mol-1) with An3+/4+.

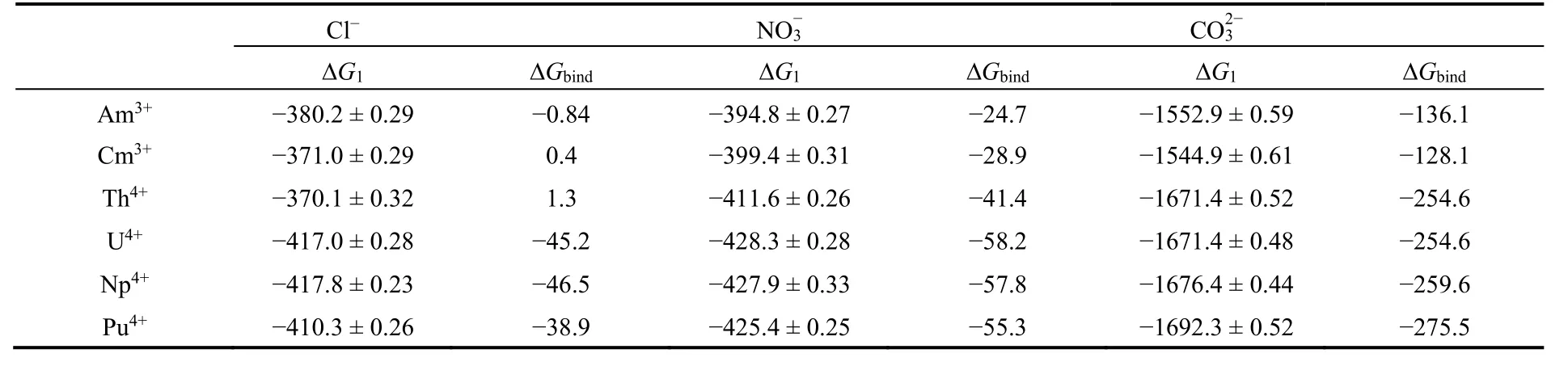
表6 热力学循环计算过程中Cl-、、溶剂化能ΔG2及其与An3+/4+的复合化能ΔG1、结合自由能ΔGbind (单位：kJ·mol-1)Table 6 The anion’s complexation free energy ΔG1 and binding free energy ΔGbind (in kJ·mol-1) with An3+/4+.

a The anion’s hydration free energy ΔG2 were calculated to be -371.8 ± 0.24 kJ·mol-1 for Cl-, -370.1 ± 0.21 kJ ·mol-1 for NO-3,and -1416.8 ± 0.52 kJ·mol-1 for, respectively.

Cl- NO3- CO3 2-ΔG1 ΔGbind ΔG1 ΔGbind ΔG1 ΔGbind Am3+ -380.2 ± 0.29 -0.84 -394.8 ± 0.27 -24.7 -1552.9 ± 0.59 -136.1 Cm3+ -371.0 ± 0.29 0.4 -399.4 ± 0.31 -28.9 -1544.9 ± 0.61 -128.1 Th4+ -370.1 ± 0.32 1.3 -411.6 ± 0.26 -41.4 -1671.4 ± 0.52 -254.6 U4+ -417.0 ± 0.28 -45.2 -428.3 ± 0.28 -58.2 -1671.4 ± 0.48 -254.6 Np4+ -417.8 ± 0.23 -46.5 -427.9 ± 0.33 -57.8 -1676.4 ± 0.44 -259.6 Pu4+ -410.3 ± 0.26 -38.9 -425.4 ± 0.25 -55.3 -1692.3 ± 0.52 -275.5

在开放体系中，空气中的CO2会溶于水相并随着体系pH的变化表现出不同的物种分布，CO32-是最为常见的物种之一。在动力学模拟中，溶液中的CO32-均以κ2模式与六种金属配位，且在整个动力学模拟时间段内保持稳定，另有7个水分子在第一配位层分别与除Th4+外的五种金属离子配位形成9配位结构，对于Th4+则有8个水分子在第一配位层形成10配位结构。根据Spezia等50基于极化力场对[Cm(CO3)3]3-的水溶液动力学的模拟研究，三个碳酸根均以双齿配位与Cm3+结合，另有3个水分子与Cm3+共形成9配位结构，配位模式与配位数与本项工作一致。作者还根据不同计算方法得出Cm3+与CO32-上的配位O原子的配位键长分别为0.234-0.241 nm (POL)、 0.241 nm (DFT)、 0.241 nm(CPMD)，略高于本项模拟工作。一项实验工作66合成并表征了[C(NH2)3]6[NpIV(CO3)5]·4H2O配合物，发现共有5个CO32-以双齿配位的模式与Np4+配位形成10配位结构，[C(NH2)3]+与H2O分布在第二配位层，并统计出10个配位氧原子与Np4+配位的平均距离为0.244 nm，比使用本文报道的参数的模拟结果大0.023 nm，但由于配合物结构相差较大，CO32-对金属配位具有较强的影响，两组数据无法进行直接对比。

为了分析An3+/4+与Cl-、NO3-、CO32-在水溶液中的结合强弱，我们采用图9所示的热力学循环来计算阴阳离子的结合自由能。由于有限尺寸给自由能计算带来的误差与微扰粒子的电荷成正相关70，为了尽可能减小该部分误差，我们选择微扰具有低价态的阴离子，而不是高价态的An3+/4+。在图9中，ΔG1和ΔG2表示目标阴离子从dummy态分别微扰到复合物水溶液和纯水溶液的自由能变化，ΔG3表示该阴离子在复合物水溶液体系及纯水体系中的空穴能差异，由于该能量差很小往往忽略不计。阴阳离子的结合自由能可以计算为：

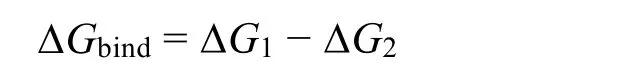
自由能计算结果表明(表6)，CO32-对An3+/4+的结合能力要远强于NO3-及Cl-，自由能微扰过程中的能量积分表明这主要来源于高电荷带来的强静电相互作用贡献(图S2)。NO3-的结合能力略强于Cl-，这主要由于Cl-与An3+/4+较高的范德华斥力导致。整体看来，静电相互作用是An3+/4+与三种阴离子的结合的主要贡献，范德华作用均表现为斥力，因此，对于同种阴离子，An4+的结合能力要高于An3+。对于An4+，Th4+与Cl-、NO3-的结合自由能要明显弱于其他三种An4+，这与Th4+较高的配位数有关(表2)。

4 结论

本文基于惰性气体的LJ势中R和ε的函数关系，以及文献报道的Np4+/Am3+/Cm3+―Ow键长的实验值，拟合出该三种锕系金属离子的AMBER力场参数并评估了其可靠性。结合已发表的Th4+、U4+、Pu4+参数，系统研究了六种锕系离子的溶液配位化学，获得了与文献一致的六种金属离子在水溶液中的水合结构。从立体化学的角度，10配位的Th4+的水合结构采取BCASP构型，9配位的U4+、Np4+、Pu4+、Am3+的第一配位层原子采用CASP的构型，而9配位的Cm3+相应原子采用TCTP构型。研究进而采用FEP方法计算了六种锕系离子的溶剂化自由能，得到了与之前工作吻合的结果，并从能量分解的角度解释了An4+的溶剂化效应要远强于Am3+及Cm3+的原因，提出这种差异主要来源于An4+与水之间较强的静电吸引作用。

采用该套力场参数，本文也分析了金属对外围水分子结构、平动与转动性质的影响，发现可以提供金属离子近程水分子的分布和运动的合理图像，并可得出与文献一致的Cm3+和Am3+的第一配位层水分子的驻留时间，但对于四价锕系离子，计算得到的驻留时间显著小于文献提供的推测值。虽然文献报道的数值自身存在较大的误差，我们谨慎建议本文报道的参数适用配位结构和结合自由能的研究；在用于动力学性质的研究时，仅可用于相同价态的锕系离子溶液体系的定性比较。另外，由于该套参数基于金属与水之间的相互作用拟合得到，宜用于金属与软硬酸碱理论中较“硬”配体的相互作用的模拟；当用于金属与较“软”配体的配合物的模拟时，可能会带来较大误差，需审慎对待。

此外，我们运用此套参数模拟了六种金属离子与重要的无机阴离子Cl-、NO3-和CO32-的溶液动力学的模拟研究，发现NO3-均以κ1模式配位，CO32-均以κ2模式配位。并通过热力学定性分析阴阳离子的结合强弱。通过对比文献报道的实验及理论研究结果，发现采用该套参数可以获得合理的配位模式、键长及结合强度等配合物结构信息，丰富我们对锕系溶液化学的认识。

Supporting Information:available free of chargeviathe internet at http://www.whxb.pku.edu.cn.