寻找“面积变化”的秘密

□戎松魁

人教版《数学》教科书五年级上册的第六单元是“多边形的面积”。与该册教科书配套的《教师教学用书》（以下简称《教学用书》）上提出了两个与面积有关的问题，一个是图形经过剪拼面积似乎变小了，另一个是图形经过剪拼面积似乎变大了。按理说，图形经过剪拼（不重叠）面积是不变的，而在这两个问题中，面积似乎发生了变化，其“秘密”何在呢？就让我们一起来寻找。

【问题1】如下图，如果将图1中的四块几何图形裁剪开来重新拼接成图2，我们将会发现，与图1相比，图2多出了一个洞！这怎么可能呢？理性会提出这样的疑问。究竟是什么原因呢？老师们不妨先动动脑，想一想。（《教师用书》第231页）

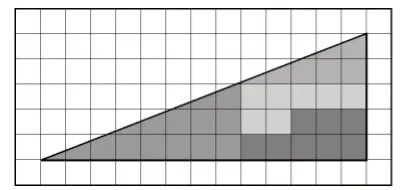
图1

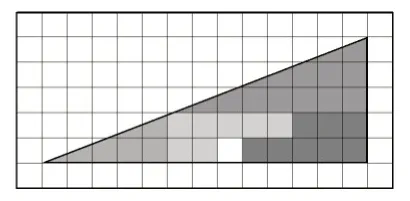
图2

【寻找秘密】从图1和图2可以直观地看到图形经过剪拼出现了一个正方形的“空缺”，面积变小了，这怎么可能呢？秘密何在？

我们把图1和图2放到直角坐标系中来研究（如图3、图4所示）。

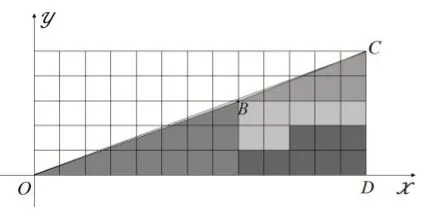
图3

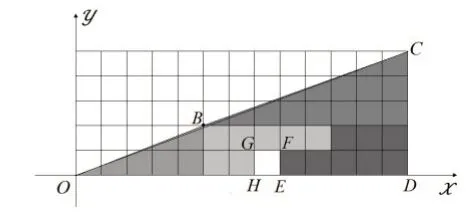
图4

为了叙述方便，而且不失一般性，我们假设每个小正方形的边长为1cm，并在多边形的顶点上标上适当的字母。

由图3可知，线段OB的斜率为，线段BC的斜率为，所以线段OB和BC不在同一直线上。连接OC，由于线段OC的斜率为，所以点B在线段OC的下方，四边形OBCD的面积为S1=

由图4可知，线段OB的斜率是，线段BC的斜率为，所以线段OB和线段BC也不在同一直线上。连接OC、OD，由于线段OC的斜率为，且，所以点B在线段OC上方。由此可知，经过剪拼得到的图形（如图4所示）其实是一个八边形，这个八边形OBCDEFGH的面积为与图3中的四边形OBCD面积相等。这就是说，剪拼前与剪拼后的图形其面积是相等的。

既然图3和图4中两个几何图形的面积相等，那么为什么我们看到图4中的图形面积要比图3中的图形面积小1cm2呢？事实上，这是因为线段OB、BC、OC的斜率相差不大，线段OB和BC的长度之和与线段OC的长度几乎相等，由这样的三条线段构成的三角形面积也很小（容易求得图3中△OBC的面积和图4中的△OBC的面积都是0.5cm2），以致使我们忽视了它们的存在（图1和图2中也确实没有把它们画出来）。因此，如果我们将图4和图3进行比较，就会发现图形在拼接后线段OC两旁分别增加了一个面积为0.5cm2的三角形，面积共增加了1cm2，因而在其他位置上就出现了一个面积为1cm2的“空缺”（正方形EFGH），保持了图形在剪拼前后面积的相等。因为大家都能清楚地看到图4中这个面积为1cm2的“空缺”，而增加的1cm2面积却很难发现（图3中的折线OBC是向下凸的，图4中的折线OBC是向上凸的），因此就觉得图3在经过剪拼后面积变小了。

顺便指出，《教师用书》上说：“与图1相比，图2多出了一个洞！”这种说法似乎欠妥。如图4所示，剪拼后得到的是一个八边形OBCDEFGH，这个图形中其实并没有洞。

【问题2】有一张8cm×8cm的正方形纸片，面积是64cm2。把这张纸片按图3所示剪开，把剪出的4个小块按图4所示重新拼合，这样就得到了一个长为13cm，宽为5cm的长方形，面积是65cm2。这是可能的吗？（《教师用书》第232页。题中的图3和图4分别是本文中的图5和图6）

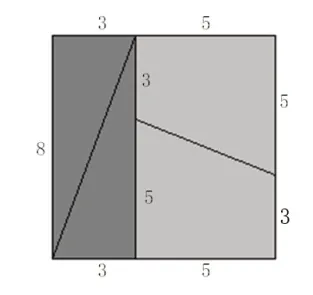
图5

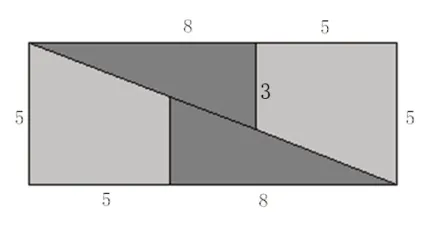
图6

【寻找秘密】这个问题其实就是出现在《义务教育数学课程标准（2011年版）》（以下简称《课标》）第119页上的“例74”。一张面积为64cm2的正方形纸片剪成4小块，居然拼成了一张面积为65cm2的长方形纸片，面积增大了1cm2，这显然是不可能的。秘密何在？

我们把如图6所示的4个多边形放到直角坐标系中来研究。为了叙述方便，在多边形的一些顶点标上适当的字母（如图7）。

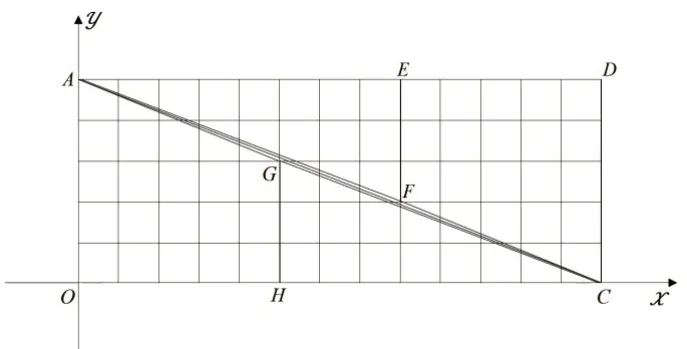
图7

由于∠GHO=∠GHC=90°，所以OH和HC在同一直线上，同理AE和ED也在同一直线上，且OC=AD，又OA=CD，所以四边形OADC是平行四边形，而∠AOC=90°，从而四边形OADC是长方形（有一个角是直角的平行四边形叫作长方形）。

由图7可知，线段AG的斜率是，而线段GC的斜率是-，因此线段AG和GC不在同一条直线上。由于两条线段斜率仅差因此肉眼难以分辨，以为它们就是对角线AC。连接AC，容易算得四边形AGCO的面积（cm2），而△AOC的面积所以△AGC的面积S3=S2-S1=0.5（cm2）。

同理可得，△AFC的面积S4=0.5（cm2）。所以四边形AGCF的面积S=S3+S4=1（cm2）。

这就是说，长方形OADC内部存在一个面积为1cm2的空隙，用“长×宽”这个公式计算长方形面积时把这个空隙的面积也算进去了，如果去掉这个空隙面积，所拼成的图形面积还是64cm2。

顺便指出，《课标》在解决这个问题时所用的方法值得商榷。

《课标》中用反证法证明了∠GCH+∠DCF≠90°，认为∠DCO不是直角（《课标》的图中∠DCO是由两个角组成的），从而说OADC不是长方形，因此不能用长方形的面积计算公式来计算面积。事实上，如果四边形OADC是长方形，所以∠DCO是直角，即∠GCH+∠GCF+∠DCF=90°。而《课标》中的证明忽视了∠GCF的存在，认为∠DCO不是直角，这显然是不对的。

退一步说，即使OADC不是长方形，也不能说它的面积一定是64cm2。这种推理方法并没有找出图5经过剪拼变成图6后面积增加1cm2的真正原因。建议《课标》在再版时修改一下。

《教师用书》中提出的这两个问题并不简单，确实值得我们深入研究。