分布式驱动电动方程式赛车扭矩分配策略

2020-12-25周增城彭育辉钟龙飞

福州大学学报（自然科学版） 2020年6期

周增城，彭育辉，钟龙飞

(福州大学机械及自动化学院，福建福州 350108)

0 引言

与集中式驱动电动汽车相比，分布式驱动电动汽车的驱动轮扭矩响应更快、扭矩控制精度和传动效率更高[1]，因而被电动方程式赛车广泛采用. 车辆在高速转弯时，横摆角速度与质心侧偏角对汽车行驶稳定性有很大的影响. 因此，对分布式驱动的电动汽车而言，如何实现车辆在高速转弯时的左右车轮的速差协调及车身稳定性是一个极其重要问题.

车辆在高速转弯时，大侧向加速度容易使车辆发生侧滑、甩尾等危险情况. 为此，通过控制各驱动轮的扭矩来提升车辆的行驶稳定性一直是研究的关注重点. 目前，控制车辆行驶稳定性的主要方法有PID控制[2]、模糊控制[3-4]、滑膜控制[5-7]、神经网络控制[8-10]及模型预测控制[11-13]等. Chen等[14]提出纵向力的动态扭矩分配策略，基于规则对单个车轮进行扭矩控制并检测车轮的附着状态，然而基于规则的扭矩分配难以适应复杂的行驶工况. Kang等[15]采用横摆力矩控制器与扭矩分配控制器组成的分层控制模块对车辆进行稳定性控制，增强了车辆抗侧滑和抗侧翻的稳定性，但算法复杂，运算量大，实时性差. Sill等[16]提出轴荷饱和度概念，通过PID算法将横摆力矩按比例分配给驱动轴，单纯的PID调节往往难以兼顾车辆复杂的动态特性，存在较大的静差. Jonasson等[17]利用横摆角速度与质心侧偏角的耦合，通过横摆角速度来调节质心侧偏角，并未考虑车轮滑动率对横向运动的影响.

基于电动方程式赛车行驶路径已知的情况，对后轮独立驱动电动赛车提出一种分层控制的扭矩分配策略，提高车辆在极限转弯与双移线工况下的行驶稳定性. 扭矩分配控制策略包含控制目标参数设计层、横摆力矩控制层和驱动轮扭矩分配及滑转率控制层. 通过Matlab/Simulink和Carsim仿真软件分别构建扭矩分配策略模型与整车模型，建立稳定性控制系统的联合仿真平台，在蛇形绕桩与双移线工况下进行仿真分析和实车测试，验证了所提扭矩分配策略的合理性与有效性.

1 整车运动模型

采用Optimum Lap软件构建赛道模型，生成车辆在绕桩及双移线行驶时的理想速度模型(如图1所示). 接着，基于Matlab/Simulink仿真平台构建驾驶员模型和驱动电机模型，将已获取的理想速度输入驾驶员模型. 最后通过Carsim软件构建整车运动仿真模型来模拟分析不同工况下的车身稳定性.

图1 蛇形绕桩与双移线工况速度分布图(单位： km·h-1)Fig.1 Velocity distribution diagram of serpentine winding pile and double moving line(unit： km·h-1)

1.1 驾驶员模型

驾驶员期望扭矩由基础扭矩与补偿扭矩组成，其中补偿扭矩利用PI算法来构建. 以目标车速与实际车速的偏差值作为模型的输入，驾驶员的补偿扭矩作为模型的输出.

Tr=Tf+Ti+Tw+Tj，e(t)=vtarget(t)-vreal(t)

(1)

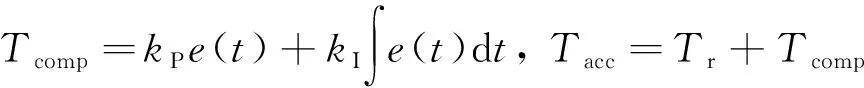
(2)

式中：Tr为整车受到的总阻力矩；Tf为受到的滚动阻力矩；Ti为受到的坡度阻力矩；Tw为受到的空气阻力矩；Tj为受到的加速阻力矩，e(t)为t时刻目标车速和实际车速的偏差；vtarget(t)为t时刻的目标车速；vreal(t)为t时刻的实际车速，Tcomp为驾驶员补偿扭矩，kP、kI分别为比例控制系数、积分控制系数；Tacc为驾驶员期望扭矩.

1.2 电机模型

电机模型通过实验建模方法来建立，驱动电机的数值模型(MAP表)通过电机台架试验获取. 驾驶员期望扭矩通过加速踏板开度信号体现，在电机外特性曲线和电池可输出的实际功率的约束下，根据电机效率特性曲线计算电机实际能够输出的最大扭矩.

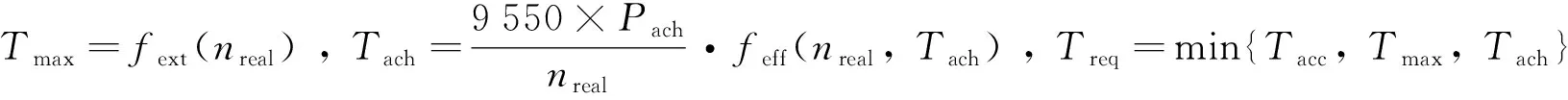
(3)

式中：Tmax为电机在特定转速下能够输出得最大扭矩；fext为驱动电机的外特性曲线；Tach为当前电池状态下电机能够输出的最大扭矩；Pach为当前电池状态下能够输出的最大功率；feff为电机的效率特性曲线；Treq为最终电机输出的扭矩.

2 扭矩分配策略

基于分层控制的扭矩分配策略包括上、中、下三层，如图2所示. 上层为基于动力学模型的控制参数设计层，负责输出两个与稳定性相关的最主要参数，即横摆角速度偏差与质心侧偏角偏差；中层为基于模糊神经网络的横摆力矩控制层，其作用是通过模糊神经网络算法与地面能够提供的最大横摆力矩限值来实时输出一个横摆力矩，修正车辆的行驶状态；下层是车辆的扭矩分配及滑转率控制层，其针对中层输入的横摆力矩转化为左右两个驱动轮的扭矩，并且对车轮的滑转率进行控制，防止车辆出现过度打滑而失控的情况.

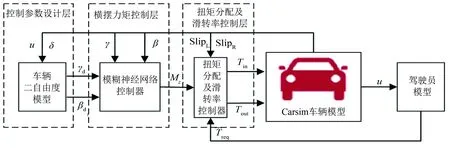
图2 控制系统结构图Fig.2 Control system structure diagram

2.1 控制参数设计层

控制参数设计层是整个扭矩分配控制系统的基础层，包含：基于稳定性行驶的目标参数制定和质心侧偏角观测器的设计.

1) 基于稳定性行驶的目标参数制定. 车辆行驶稳定性主要包括，一是机动稳定性问题，其评价指标是横摆角速度，主要是由车轮的纵向力与侧向力所产生的横摆力矩决定；其次是车轮的侧向运动引起质心轨迹偏离问题，其评价指标是质心侧偏角.

当车辆行驶处于稳定状态时，根据文[8]可知，理论横摆角速度与质心侧偏角为：

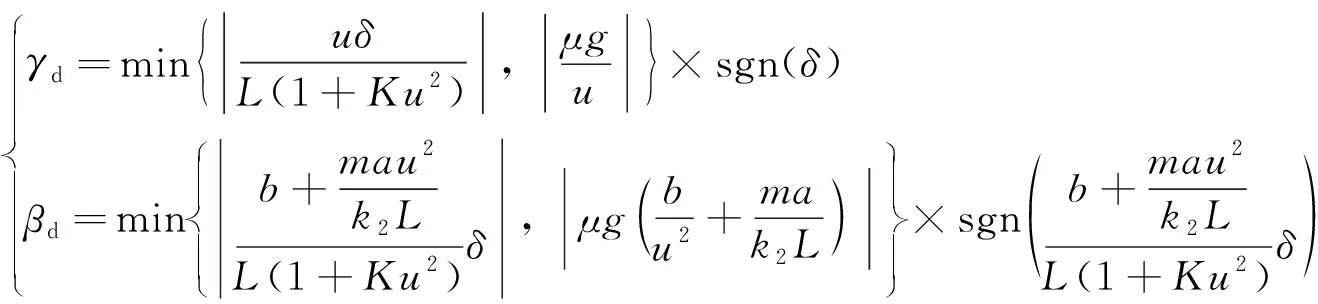
(4)

式中：k1、k2为前后轮的侧偏刚度；a、b为质心到前后轴的距离；m为汽车质量；δ为转向轮转角；u为纵向车速；v为横向车速；β为质心侧偏角；γ为横摆角速度；L为轴距；μ为路面附着系数；K为稳定性因素.

2) 质心侧偏角观测器设计. 由于实际横摆角速度可通过传感器测量得到，但是实际质心侧偏角数据无法通过传感器测量得到，因此需要设计一个质心侧偏角观测器来准确估算实时质心侧偏角. 以车辆二自由度模型为参考模型，设计状态空间观测器：

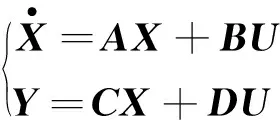
(5)

式中:

其中：Iz为车辆的转动惯量.

上述矩阵A与B是可观测的，前轮转角δ与横摆力矩Mz可由传感器测量、计算获得. 将观测得到实际侧偏角输入到控制参数设计层，计算侧偏角理想值与实际值的差值.

2.2 基于模糊神经网络的横摆力矩控制层

车辆的稳定性可以通过横摆角速度偏差与质心侧偏角偏差来进行评价，两者偏差越小，说明稳定性控制效果越好. 横摆力矩控制层采用基于Takagi-Sugeno型的模糊神经网络算法[10]，其结构图如图3所示. 采用5层的模糊神经网络，输入层为横摆角速度的偏差e(γ)和质心侧偏角的偏差e(β)，输出层为横摆力矩Mzf，输入输出层的隶属度函数均采用gaussmf.

通过横摆力矩Mzf与地面能够提供的最大横摆力矩Mzmax进行比较，得到最终的横摆力矩Mz进行车辆的控制. 模糊神经网络通过在线学习输入变量e(γ)、e(β)与输出变量Mzf的关系，能够快速有效地计算出隶属度函数的最佳参数, 同时, 生成25条模糊规则语句，构成控制器的模糊规则库，如图4所示.

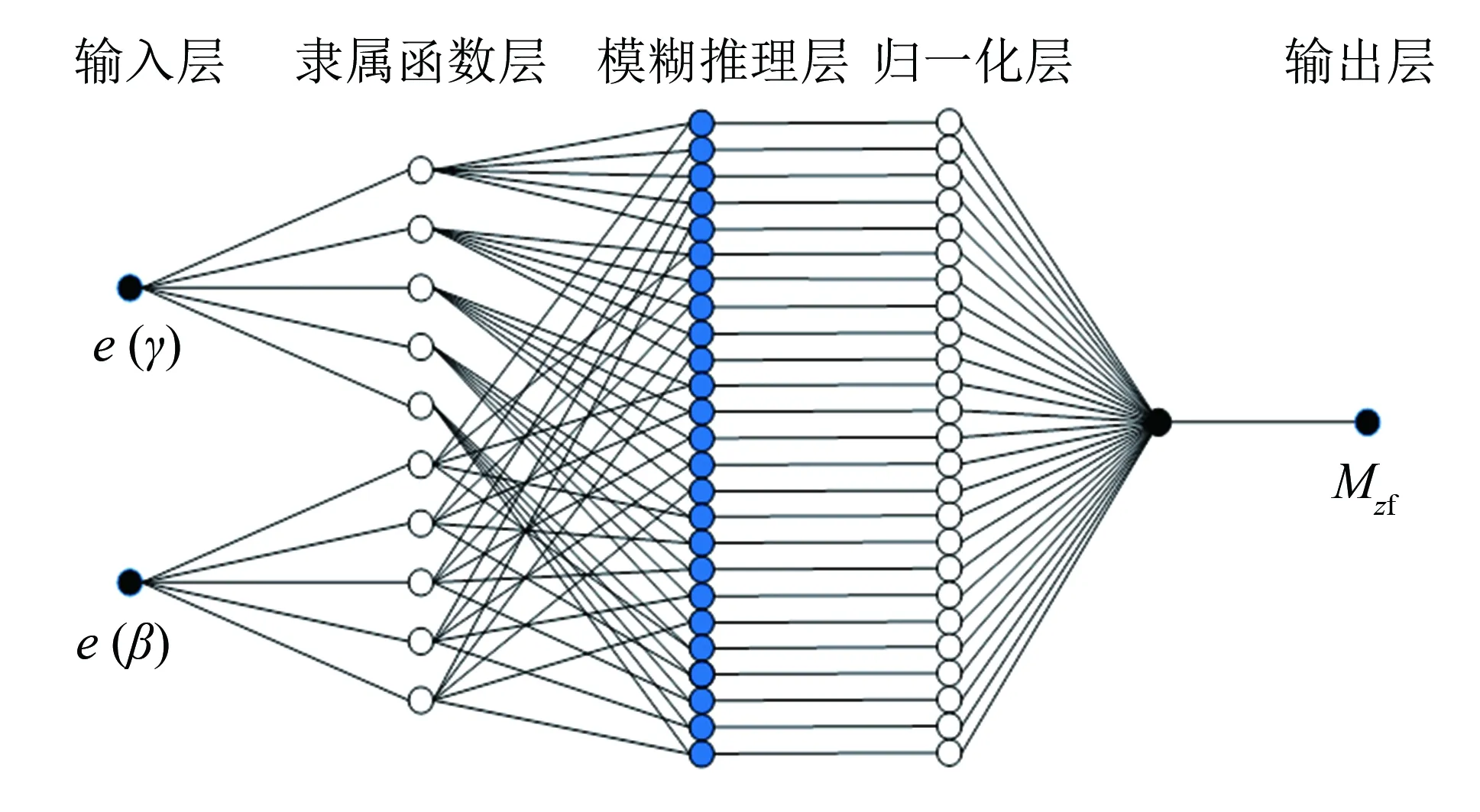
图3 模糊神经网络结构示意图Fig.3 Structure diagram of fuzzy neural network

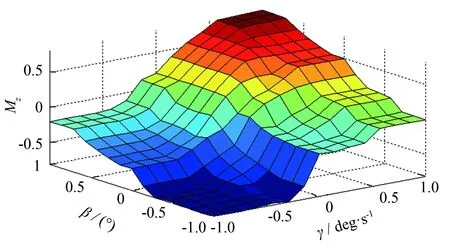
图4 训练后模糊规则库Fig.4 Fuzzy rule base after training

在车辆行驶的过程中，模糊神经网络控制器会对车辆施加一个横摆力矩使车辆稳定行驶. 如果该力矩超过地面作用在车轮上的力矩限值时，车轮会发生过度滑转现象，因此需要对横摆力矩进行限制. 地面能够提供的最大横摆力矩为：

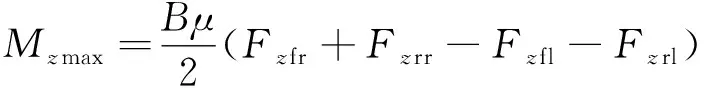
(6)

式中：B为轮距；Fzfr、Fzrr、Fzfl、Fzrl分别是右前轮、右后轮、左前轮、左后轮的纵向力. 根据比较模糊神经网络输出的横摆力矩与计算地面能够提供的最大横摆力矩，将其中较小的力矩作为最终的横摆力矩Mz，

Mz=min{Mzf,Mzmax}

(7)

2.3 扭矩分配与滑转率控制层

扭矩分配及滑移率控制层接受来自驾驶员模型计算的期望扭矩及横摆控制层输出的横摆力矩对驱动轮进行扭矩分配，同时考虑电机故障及驱动轮滑转率因素. 若电机发生故障，产生两侧驱动轮输出不同的扭矩，存在循迹困难甚至失控风险；若车辆的滑转率过大，容易造成车辆失控而发生事故. 因此，扭矩分配策略中需考虑到电机故障及滑转率的因素，确保车辆稳定行驶.

1) 扭矩分配及约束. 为保证车辆行驶的稳定性，通过控制驱动轮的扭矩给车辆施加一个目标横摆力矩Mz. 采用对外侧轮增加ΔT，内侧轮减少ΔT的方式进行控制. ΔT的计算如下：

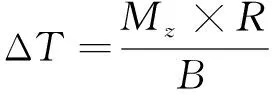
(8)

式中：R为轮胎半径.

考虑到电机最大扭矩的限制，两侧驱动轮的期望扭矩为：

式中：T1与T2分别表示内外侧电机的实际输出扭矩；T1_max与T2_max分别表示此时电机内外侧能够输出最大的扭矩；nr为电机额定转速；n为电机实际转速.

2) 电机故障. 当电机发生故障时，电机会向电机控制器发送故障码，根据故障等级的不同，需要设计电机故障因子ξ来约束驱动轮的扭矩，防止损坏电机及驱动器. 故障因子ξ的范围是[0， 1]， 0表示电机故障等级最高，电机失效，需立即停车； 1表示电机无故障，正常运转. 电机的故障等级由电机编码器发送给电机控制器的故障码进行评判. 在电机故障因子的约束下，内外侧驱动轮输出的扭矩为：

Ti≤ξiTi_max(i=1, 2)

(12)

3) 滑转率控制. 根据实际路面情况，将目标滑转率设置为[0.05 0.2]. 采用基于逻辑门限的滑转率控制策略，通过采集实时的滑转率与目标滑转率进行比较，当车轮滑转率超过设定值时，启动电机的扭矩PID控制，以滑转率的差值作为输入调节电机扭矩输出.

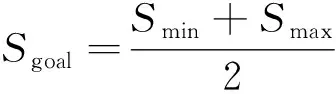
(13)

式中：Smin与Smax分别为目标滑转率范围的最小值与最大值；Sgoal为目标滑转率. 采用PID控制的算法中，调节的扭矩大小为

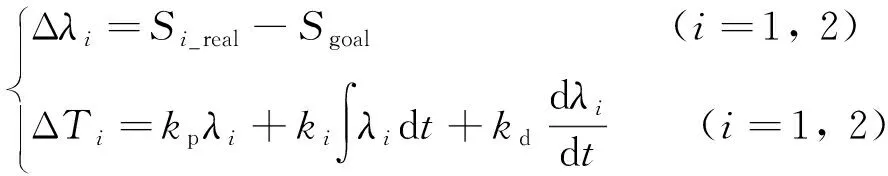
(14)

式中：kp、ki和kd分别为比例、积分和微分系数. 最终输出的扭矩为

(15)

式中：Tin与Tout分别为内侧轮与外侧轮的扭矩.

3 仿真分析与实验验证

基于Matlab/Simulink和Carsim软件建立整车运动联合仿真平台，分别对蛇形绕桩和双移线行驶工况进行仿真分析，车辆的主要参数见表1.

表1 电动赛车仿真模型参数

3.1 蛇形绕桩工况

在Carsim中设置好车辆的目标行驶轨迹，根据获得的理想车速，车辆由静止开始加速到38 km·h-1，然后进入绕桩工况，地面附着系数为0.8. 分别对驱动轮扭矩采用FNN控制、模糊控制及无控制情况进行分析，得到了各自情景下的车辆行驶轨迹、横摆角速度、质心侧偏角及车轮滑转率的曲线，如图5所示. 实车测试结果如图6所示.

由图5可知，在FNN控制策略作用下，车辆轨迹离理想的目标轨迹偏差0.81 m(在最后一个桩桶位置)，横摆角速度与期望值的延迟为0.11 s，质心侧偏角最大值为0.81°，最大车轮滑转率为0.126；如果采用模糊控制算法进行扭矩分配，则车辆轨迹离理想的目标轨迹偏差2.04 m，横摆角速度与期望值的延迟为0.29 s，质心侧偏角为1.02°，最大滑转率达到了0.201. 由图6可以看出，实车测试得到系统动态响应曲线基本与仿真曲线一致. 由此，所提的扭矩控制策略能有效提升赛车在蛇形绕桩工况下的稳定性和跟随性.

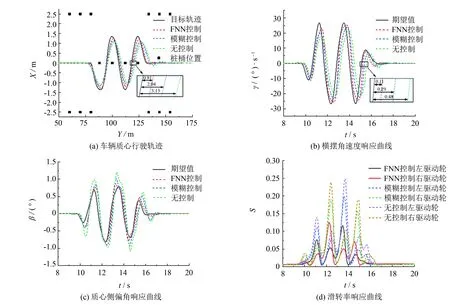
图5 蛇形绕桩工况仿真结果Fig.5 Simulation results of snake driving condition

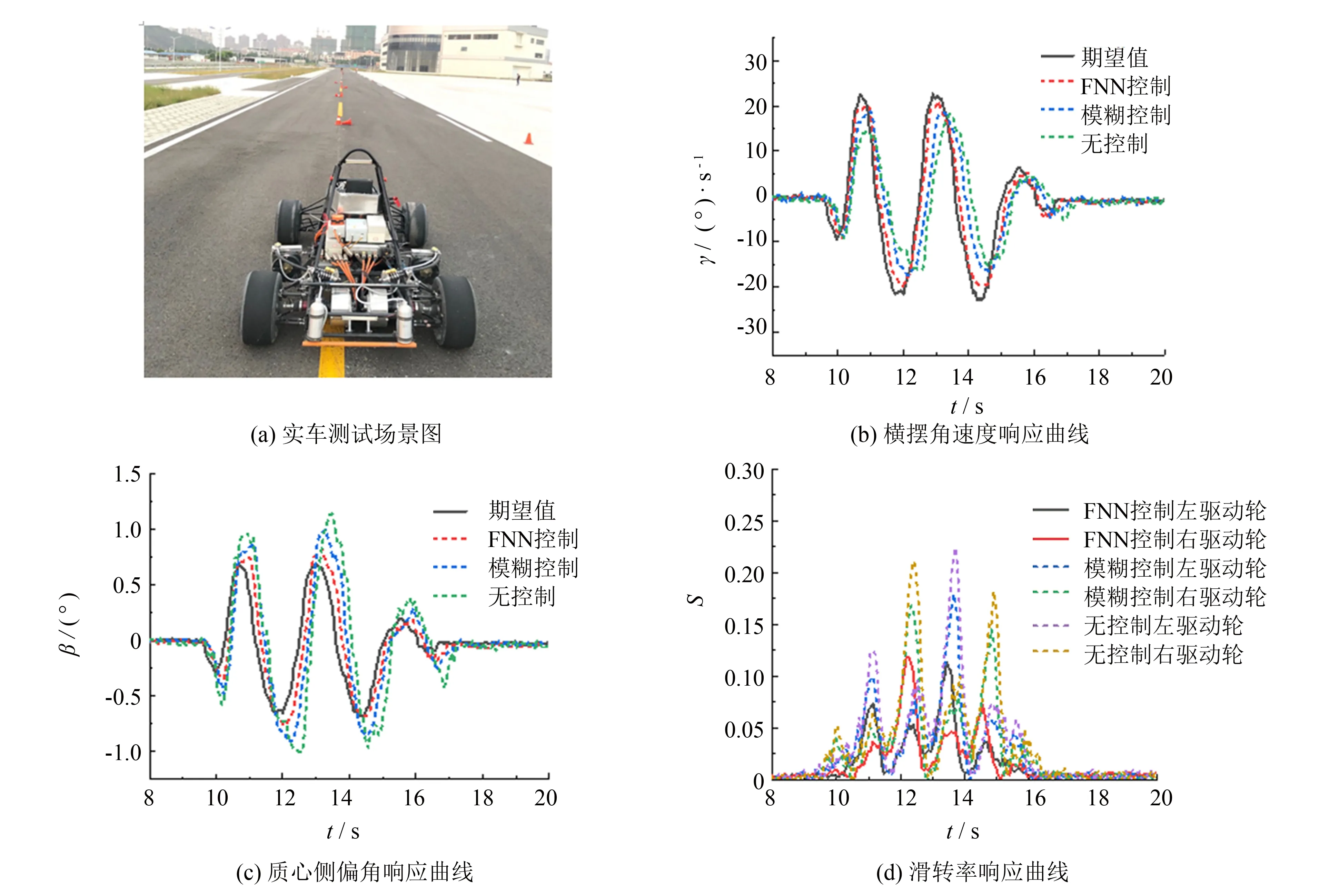
图6 蛇形绕桩工况实车测试结果Fig.6 Experimental results of snake driving condition

3.2 双移线工况

车辆由静止开始加速到65 km·h-1，然后进入双移线工况，地面附着系数为0.8，分别对驱动轮扭矩采用FNN控制、模糊控制及无控制情况进行分析，得到各自情景下的车辆行驶轨迹、横摆角速度、质心侧偏角及车轮滑转率的曲线，如图7所示. 实车测试结果如图8所示.

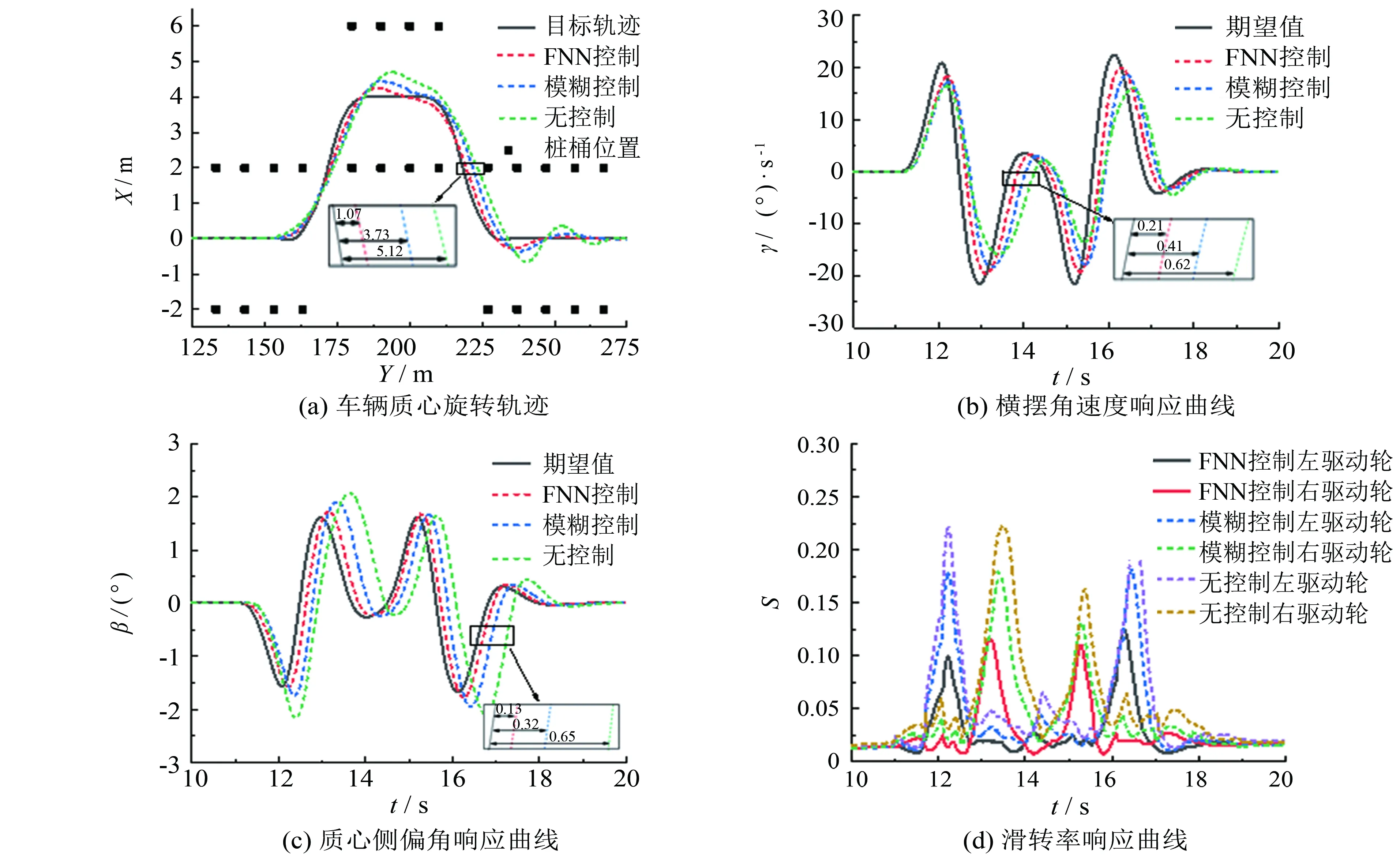
图7 双移线工况仿真结果Fig.7 Simulation result of double-line moving condition

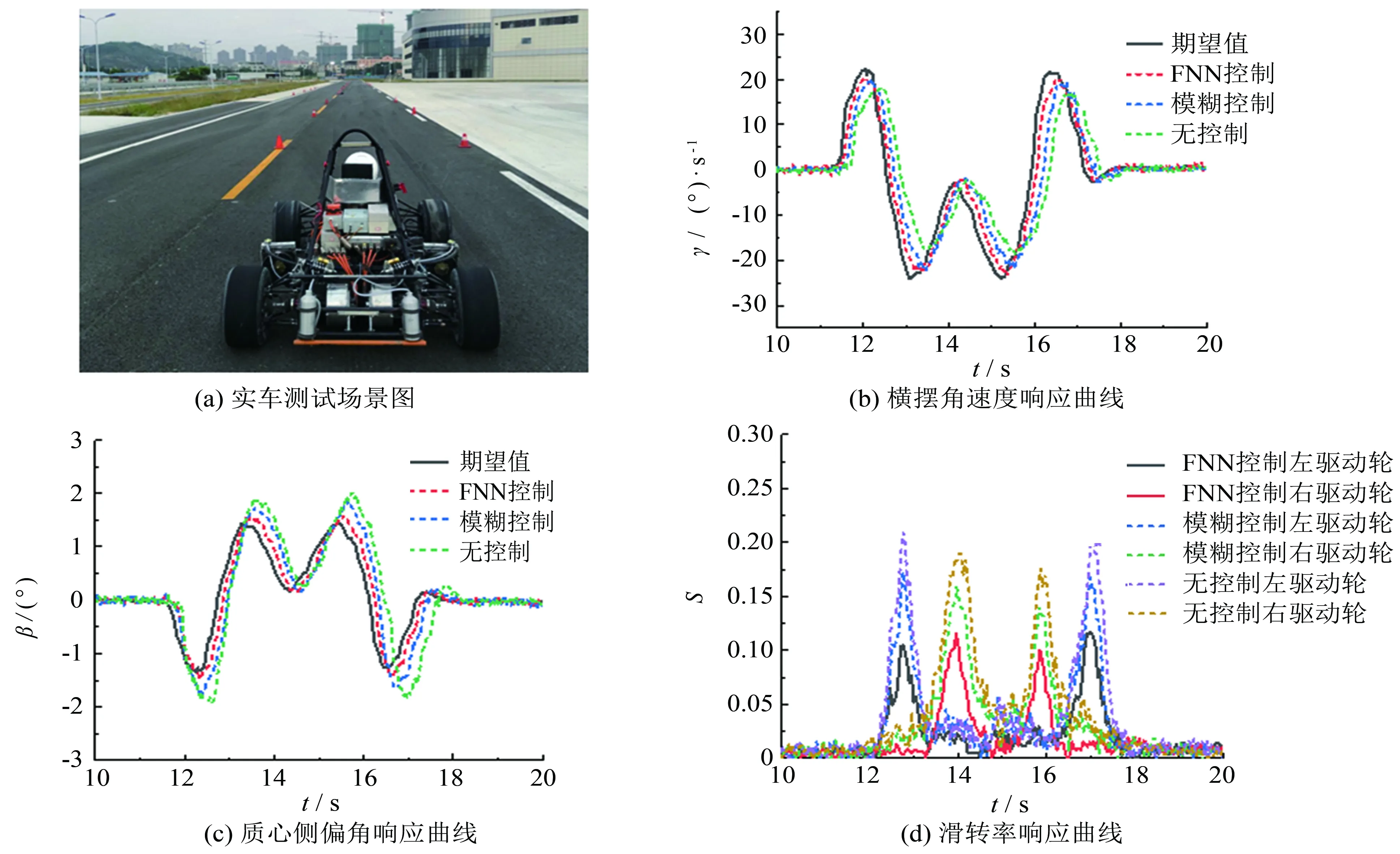
图8 双移线工况实车测试结果Fig.8 Experimental results of double-line moving condition

由图7可知，在FNN控制策略作用下，车辆轨迹离理想的目标轨迹偏差1.07 m(在第二次变道位置)，横摆角速度与期望值的延迟为0.21 s，质心侧偏角最大值为1.85°，最大车轮滑转率为0.131. 如果采用模糊控制算法进行扭矩分配，则车辆轨迹离理想的目标轨迹偏差3.73 m，横摆角速度与期望值的延迟为0.41 s，质心侧偏角为1.98°，最大滑转率达到了0.192. 由图8可以看出，实车测试得到系统动态响应曲线与仿真曲线之间偏差较小，所采用的扭矩控制方法能有效提升赛车在双移线工况下的稳定性和跟随性.