结合频率预测的虚拟同步发电机自适应参数控制策略
2020-12-25李天扬温步瀛王怀远
李天扬, 温步瀛, 王怀远
(福州大学电气工程与自动化学院, 福建省新能源发电与电能变换重点实验室, 福建 福州 350108)
0 引言
随着全球能源危机和环境问题的日益加剧, 基于可再生能源的分布式发电系统覆盖率不断提高. 但是与传统电网中的同步发电机相比, 作为分布式能源与电网连接的枢纽, 并网逆变器存在容量小、 缺乏惯性和阻尼特性等缺陷. 随着大量分布式能源接入电网, 电力系统运行的稳定性问题变得日益严峻[1-2].
借鉴同步发电机的一次调频和一次调压特性, 有学者提出了下垂控制策略[3-4]. 在孤岛模式下, 各分布式电源可以根据自身的额定容量实现负荷功率的均分. 在并网模式下, 基于下垂控制的并网逆变器可以为受扰动的电网提供一定的功率支撑.
然而, 基于下垂控制的并网逆变器仍然没有惯性支撑能力. 因此, 虚拟同步发电机(virtual synchronous generator, VSG)控制策略被提出[5-8], 通过在逆变器控制算法中加入转子的运动方程, 增大系统的惯性, 提高了系统对频率和电压的支撑能力. 但是常规的VSG无法应对各种复杂的工况, 需要对VSG的结构或参数设定加以改进. 文[9-11]通过改变有功环的控制结构, 改善逆变器输出频率和功率的动态特性. 文[12]通过在线优化整定虚拟转动惯量和阻尼系数. 文[13]在频率偏离稳态值时采用较大的转动惯量, 在频率返回稳态值时采用较小的转动惯量, 提高了系统的稳定性. 文[14]在频率恢复稳态时基于频率偏差量增大阻尼系数, 使频率更快恢复稳定.
虚拟转动惯量和阻尼系数是VSG有功环中两个重要的参数. 本研究在VSG中加入频率预测模块, 获取受扰动后频率的最低或最高值. 基于预测的频率值, 在扰动初期增大转动惯量和阻尼系数的整定范围, 为自适应参数控制策略提供基础, 从而改善频率和输出功率的响应特性. 最后, 通过仿真验证所提控制策略的有效性.
1 VSG控制结构
VSG的主电路拓扑和控制框图如图1所示. 逆变器直流侧电压由分布式电源和储能单元提供. 图中: Lf为逆变器滤波电感; Cf为滤波电容; Rg和Lg为电网侧的线路阻抗;ea、eb、ec为逆变器桥臂中点电压;ia、ib、ic为逆变器输出电流;ua、ub、uc为逆变器输出电压;uga、ugb、ugc为电网侧电压;E和δ分别为从VSG模块得到的参考电压幅值和功角指令值, 经过电压电流闭环控制得到三相调制波ema、emb、emc.
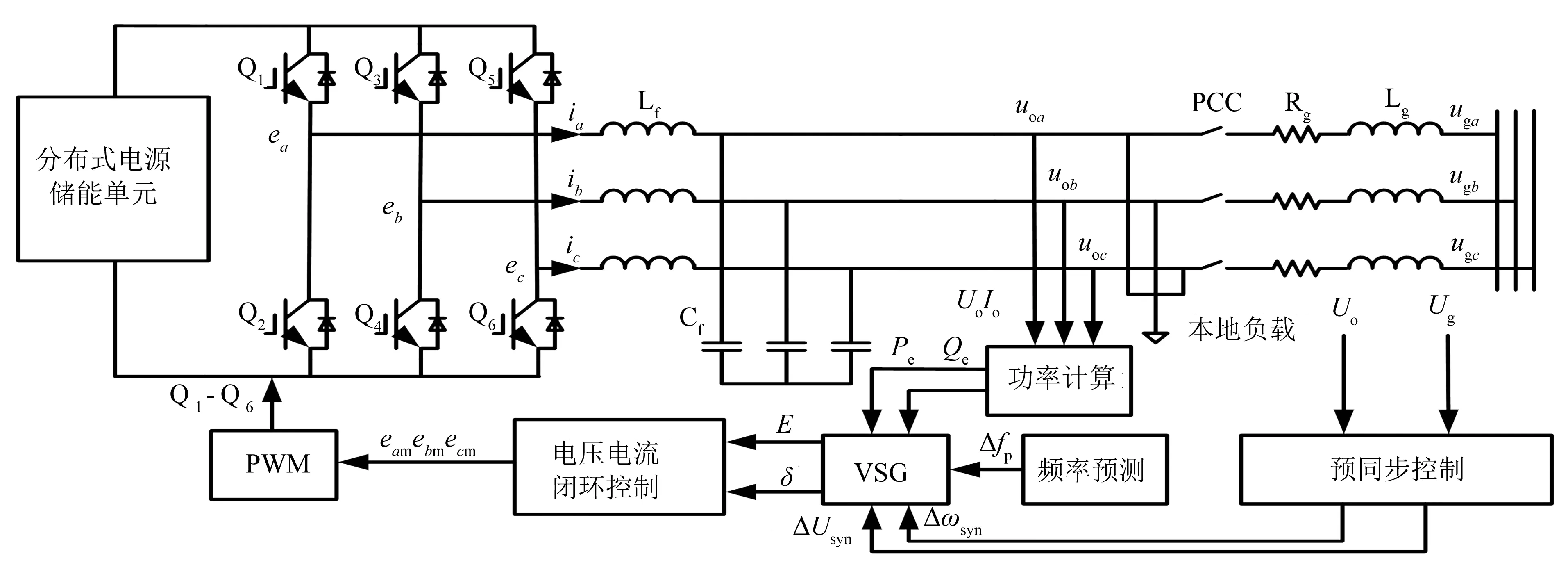
图1 VSG主电路拓扑和控制框图Fig.1 Topology and control block diagram of VSG
有功环通过模仿同步发电机的转子运动方程, 使逆变器具有转子惯性和阻尼作用. VSG有功环可表示为
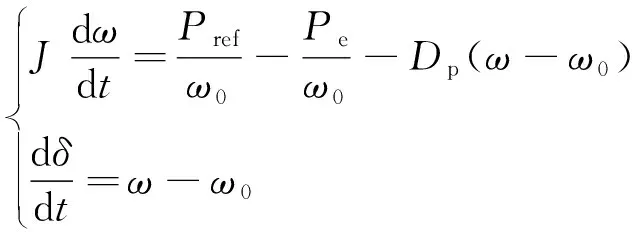
(1)
式中:J为虚拟转动惯量;Pref和Pe为VSG的有功功率给定值和输出功率;ω为输出角速度,ω0为额定角速度;Dp为虚拟阻尼系数.
2 频率预测模块
电力系统频率是电能质量的重要指标之一. 当系统中发生功率不平衡扰动时, 快速准确地预测扰动后的频率特征值, 有助于后续控制策略的改进. 频率在线预测的关键是准确获取频率变化过程中的最低值或最高值. 随着人工智能的发展, 深度学习被广泛应用于各个领域. 相对于浅层学习方法, 深度学习拥有更强的特征提取、 分类和预测能力. 文[15]提出将深度学习与电力系统频率预测相结合, 从而可以快速获取扰动后系统的频率曲线.
频率预测模块的具体流程为: 分别构建预测量为频率最低值和频率最高值的深度学习模型, 算法选用可以处理时间序列数据的长短期记忆网络(LSTM), 输入特征量选取与输出频率相关的参数, 包括逆变器的输出有功和无功, 有功和无功的给定值以及负荷水平. 通过Python调用Matlab/Simulink软件建立仿真模型. 当预测量为频率最低值时, 第一次将负荷从2.000 kW突增至2.005 kW, 第二次负荷从2.000 kW突增至2.010 kW, 即每次负荷增加量依次增加5 W, 最后负荷从2.000 kW增至10.000 kW, 总共得到1 600个仿真样本, 包括预测模型的输入特征量和输出量频率.
利用Matlab对样本数据进行归一化处理, 并随机分为1 200个训练样本和400个测试样本. 将训练样本放入LSTM模型进行训练, 直到训练误差满足要求, 获得扰动后的频率预测模型. 再将测试样本放入到训练完成的预测模型中, 根据输出的绝对误差e判断所建模型是否符合要求. 绝对误差e的定义如下:
e=fp-fa
(2)
式中:fp为预测的频率最低值或最高值;fa为实际的频率最低值或最高值. 若e≥± 0.01 Hz, 则调整模型中的参数, 直到e小于设定值要求, 最后得到可准确预测系统频率的模块.
3 VSG参数自适应控制策略
3.1 虚拟转动惯量控制策略
在VSG中, 当系统中输入功率和输出功率不平衡时, 储能装置通过充放电为系统提供等效的转动惯量, 即模拟转子动能的变化, 从而平抑扰动后出现的功率缺额, 减缓频率的变化速度. 当J较小时, 系统无法为频率提供足够的惯性支撑. 当J增大后, 频率的振荡幅度降低, 但是功率的超调会增大, 不仅使储能系统承受较大的功率冲击, 同时VSG的输出功率也可能超出逆变器的额定容量限制, 而且逆变器不具备同步发电机较强的过载能力, 电力系统运行的稳定性可能会受到影响. 因此需要合理设计J的取值范围和控制策略.
当电力系统中出现功率不平衡时, 同步发电机通过释放转子动能弥补功率缺额. 在频率变化过程中, 频率只会在较小的范围内波动. 而储能装置则可以在较大范围内进行功率的释放和吸收, 因此只需较小的储能容量即可达到与同步发电机相同的调频能力[16]. 电网运行准则规定, 系统频率变化范围为49~51 Hz. 故同步发电机所能释放的转子动能最大值为
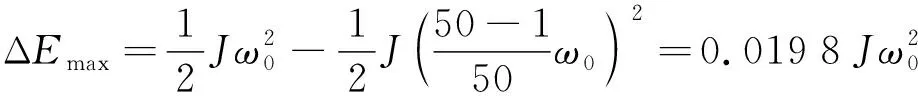
(3)
当系统中频率变化时, 使储能装置所释放的能量与同步发电机所释放的转子能量相同, 即储能装置只需配置ΔEmax的能量, 就可以产生与同步发电机相同的惯量作用效果.
上述整定原则是基于无法预测系统受扰动后频率变化的波动范围, 所以采用频率允许的最大变化量1 Hz来整定储能容量. 在VSG控制系统中加入频率预测模块后, 当系统中出现功率不平衡时, 通过预测模块快速预测频率变化量的最大值. 系统实际所需储能容量可表示为
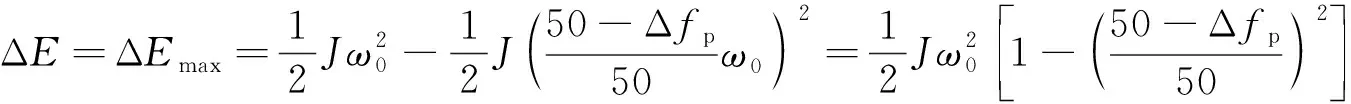
(4)
式中: Δfp是频率实际预测的最大变化量. 当Δfp<1 Hz时,J拥有更大的取值范围:

(5)
由式(5)可知, 当实际频率变化范围小于额定值时, 在储能系统所释放的最大能量不变的前提下, 使得J拥有更大的整定范围. 但是J越大, 二阶系统响应的调节时间越长, 因此需要根据调节时间的限制设定J的另一个最大值Jmax2. 具体的整定方法将在下一节给出.
将式(1)变形可得:
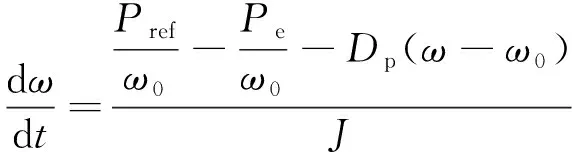
(6)
由式(6)可知, 频率的变化率与转动惯量成反比. 在频率的加速阶段, 采用较大的J, 从而限制频率变化率的增加. 在频率的减速阶段, 采用较小的J, 可使频率变化率增大, 从而使频率更快恢复稳态区间[13]. 自适应转动惯量控制策略为
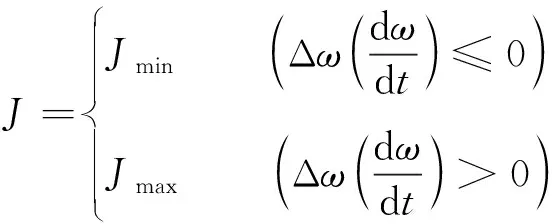
(7)
式中:Jmin为J的最小值;Jmax为J的最大值, 其值取Jmax1和Jmax2两者之间的较小值, 这样既能保证储能设备提供足够的能量, 又能保证控制系统的调节时间符合要求.
3.2 阻尼系数控制策略
上一小节提到逆变器连接电网后正常工作的条件为: 系统频率维持在49~51 Hz. 同时, 阻尼系数应与逆变器的额定容量成正比配置. 假设单台逆变器的额定容量Sn=10 kV·A. 当电网频率最大变化1 Hz, 逆变器输出有功功率最多变化100%(ΔPmax=10 kW). 根据上述原则, 整定VSG的初始阻尼系数为
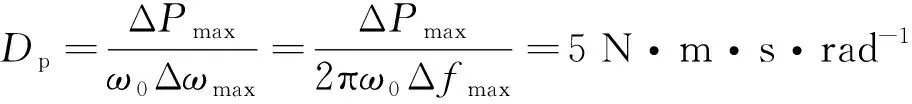
(8)
式中: ΔPmax是有功功率最大变化量; Δωmax和Δfmax分别是角速度和频率最大变化量, Δfmax=1 Hz.
同样, 该整定原则是基于无法预测系统受扰动后频率变化范围, 所以用频率最大变化量1 Hz来整定阻尼系数. 该整定方法可以保证逆变器输出功率不会超过容量上限, 但是整定的Dp可能过小, 从而无法提供足够的阻尼功率抑制频率和功率波动. 根据自动控制原理[17], 当二阶系统处于欠阻尼范围内时, 系统响应的超调量和调节时间随着Dp的增大而减小, 故适当增大Dp, 可以改善系统的响应特性.
在VSG中加入频率预测模块后, 用预测的实际频率最大偏差量代替系统所允许的最大偏差量. 当实际最大偏差量Δfp小于额定值Δfmax时,Dp能取到比初始值更大的值:
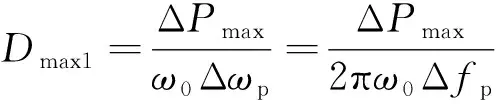
(9)
式中: Δωp是预测的角速度最大偏差量.
但是当Dp较大时, 二阶系统可能会从欠阻尼系统变为过阻尼系统, 从而减缓系统响应速度, 因此需要根据系统阻尼比范围的要求设定Dp的另一个最大值Dmax2, 整定方法在下节给出. 自适应阻尼参数的最终整定值如下式所示:
Dmax=min{Dmax1,Dmax2}
(10)
由式(10)可得,Dmax取Dmax1和Dmax2两者之间的较小值, 这样既能保证逆变器输出有功不会超过其额定值, 又能保证二阶系统运行在欠阻尼范围内, 从而使控制系统具有适当的阻尼和较快的响应速度.
4 参数整定
4.1 孤岛运行模式
在孤岛模式下, 电网无法为逆变器的输出频率提供支撑, 因此主要的控制目标是使VSG的输出频率具有良好的动态响应和稳态特性. 根据式(1)可得, 孤岛模型下频率变化量与有功功率变化量之间的关系:

(11)
选取实际响应与稳态输出之间的误差Δ=0.02, 通过式(11)可以得到自然振荡角频率ωni和阻尼比ζi以及二阶系统的调节时间tsi:

(12)
根据GB/T 31464-2015《电网运行准则》[18], 发生频率故障时, 机组的调频功能需要在3 s内开始响应. 令有功-频率环G1(s)的调节时间tsi<1 s, 取Dp=5 N·m·s·rad-1, 可得Jmax2=0.56 kg·m2. 为使二阶系统保持在欠阻尼范围内, 令0<ζi<1, 取ki=1 200,Dp=Dmax2=30 N·m·s·rad-1, 可得Jmin, i=0.187 5 kg·m2.
4.2 并网运行模式
在并网模式下, 电网是无穷大电源, 从而为逆变器的输出频率提供支撑. 当出现电网频率扰动或逆变器给定功率扰动时, VSG的输出功率可能会发生振荡或超调, 因此主要目标是使VSG的输出功率具有较好的响应特性. 并网系统的简化拓扑结构如图2所示, 图中E∠δ为分布式电源的电压,E为相电压有效值,Z为VSG到公共耦合点之间的等值阻抗,R和X分别为等值电阻和等值电抗,U∠0为公共耦合点的电压.
为简化分析, 将有功环和无功环当作近似解耦. 假设系统等效输出阻抗为感性, 即X远大于R. 同时
忽略内环响应对有功环的影响和功率计算的延时影响. VSG的输出有功功率闭环控制框图如图3所示, 其中:Kp=3EU/X.
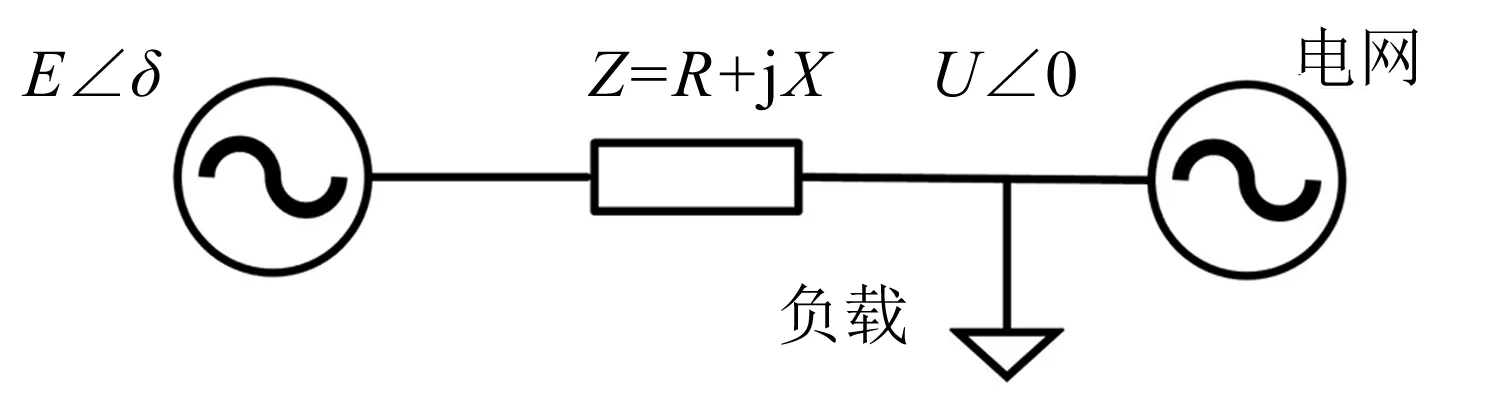
图2 VSG并网模式的简化结构 Fig.2 Simplified structure of VSG grid connection mode
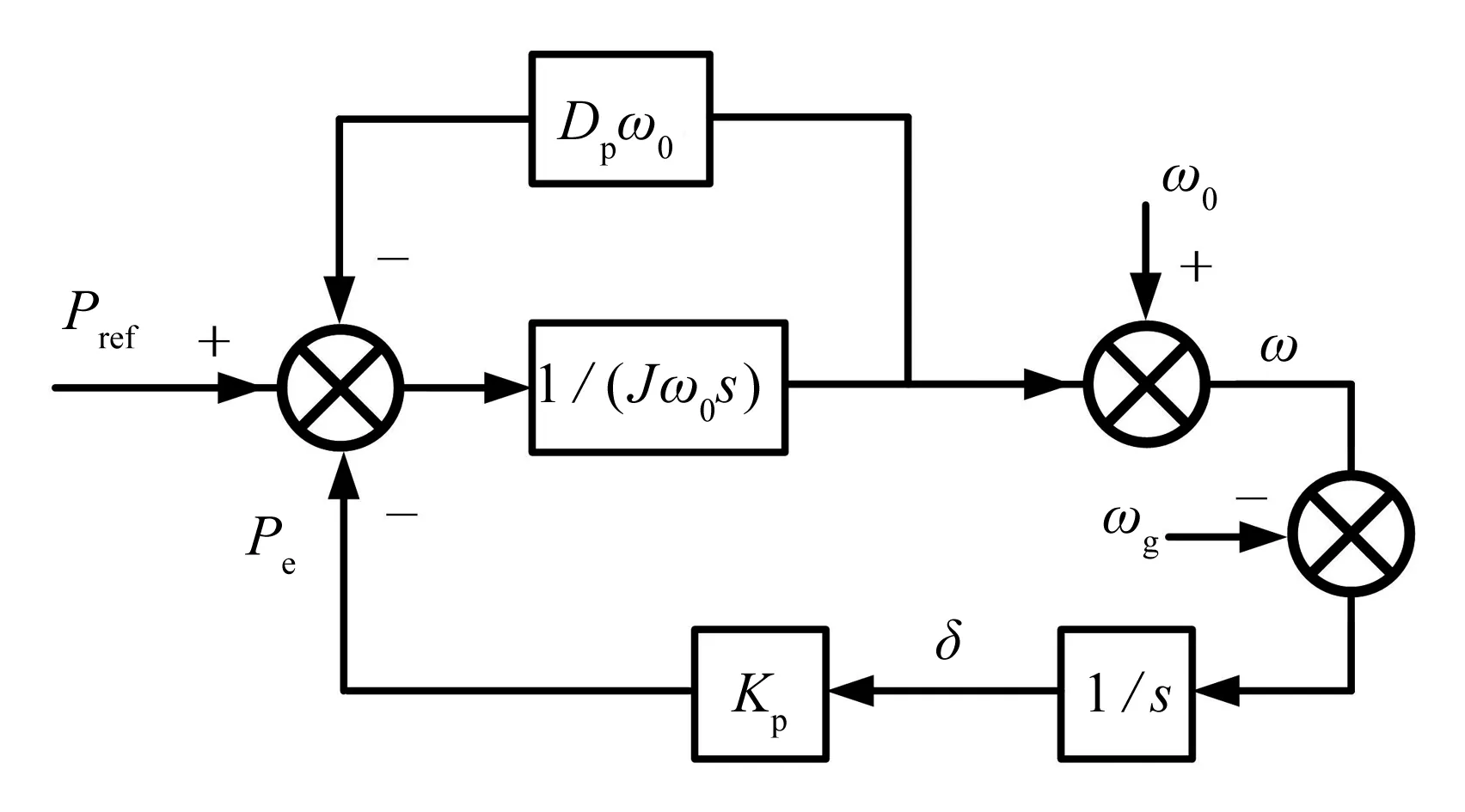
图3 VSG的输出功率闭环控制框图Fig.3 Output power closed-loop control block of VSG
由控制框图可得VSG输出功率的闭环传递函数:

(13)
式(13)为典型的二阶系统, 由此可以得到自然振荡角频率ωng和阻尼比ζg以及调节时间tsg:
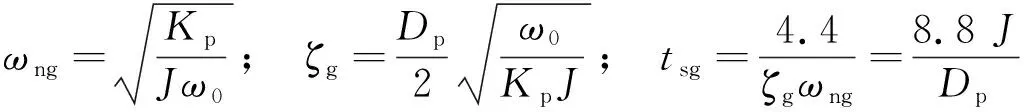
(14)
由式(12)和式(14)可得, 并网模式下功率环G2(s)的调节时间tsg和孤岛模式下有功-频率环G1(s)的调节时间tsi表达式相同, 令G2(s)的调节时间tsg<1 s, 取Dp=5 N·m·s·rad-1, 从而可得Jmax2=0.56 kg·m2. 令并网模式下功率环保持在欠阻尼范围内, 令0<ζg<1, 取Kp=7.7×105,Dp=Dmax2=30 N·m·s·rad-1, 可得Jmin, g=0.09 kg·m2.
5 仿真验证

表1 VSG系统参数设置
为验证所提控制策略的有效性, 通过Matlab/Simulink搭建仿真模型, 仿真参数如表1所示. 在孤岛模式下, 通过某时刻突变负载, 模拟系统负荷变动所引发的频率稳定性问题. 对于负载突增的算例, 初始时刻接入有功负载2 kW, 0.6 s时负载突增至10 kW. 常数转动惯量取J=0.3, 常数阻尼系数取Dp=5 N·m·s·rad-1. 在J和Dp分别取常数时, 加入频率的预测模型, 负载突增到10 kW后, 频率的最低值为49.82 Hz. 对于自适应J控制策略, 取稳态值J=0.3 kg·m2, Δfp=0.18 Hz, 代入式(3)和式(5), 得到Jmax1=1.65>Jmax2=0.56 kg·m2, 故取Jmax=0.56 kg·m2. 对于自适应Dp控制策略, 取Δfp=0.18 Hz, 代入式(9), 可得Dmax1=27.78 四种控制策略的效果如图4所示. 频率的稳态区间设定为± 0.02 Hz. 当J和Dp分别为常数时, 频率的超调量和调节时间最大, 分别为0.36%和0.29 s. 当J采用自适应策略,Dp为常数时, 其超调量和调节时间减少为0.28%和0.11 s. 当J为常数,Dp采用自适应策略时, 其超调量为0.22%, 调节时间也明显减少至0.06 s. 当J和Dp都采用自适应控制时, 频率的超调量最小, 为0.18%. 对于负载突减的算例, 初始时刻接入有功负载10 kW, 0.6 s时负载突减至2 kW. 控制效果如图5所示. 四种控制策略的效果基本与负载突增时相同. 相对于其余三种控制策略, 当J和Dp都采用自适应策略时, 频率能更快恢复稳态. 并网模式下, 0.4 s时VSG的有功功率指令值Pref从4 kW调整为10 kW. VSG的输出功率和频率分别如图6和图7所示. 当Pref改为10 kW时, 频率最高值为50.09 Hz. 对于自适应J策略, 同样取J=0.3 kg·m2, Δfp=0.09 Hz, 代入式(3)和式(5), 得Jmax1=3.30>Jmax2=0.56 kg·m2, 取Jmax=0.56 kg·m2. 对于自适应Dp策略, 取Δfp=0.09 Hz, 代入式(9), 得Dmax1=55.56>Dmax2=30 N·m·s·rad-1, 故取Dmax=30 N·m·s·rad-1. 由图6可得, 当有功功率指令突然增大时, 恒定参数控制、 自适应J和常数Dp控制、 常数J和自适应Dp控制、 自适应J和Dp协调控制的有功超调量分别为29%、 16%、 12%、 8%, 调节时间分别约为0.38、 0.23、 0.26、 0.19 s. 图6 有功指令突增时输出有功曲线Fig.6 Output power curves when active power command increases 由图7可得, 自适应J和常数Dp控制时, 频率的超调量相对于恒定参数控制减少至0.16%. 常数J和自适应Dp控制时, 频率的超调量和调节时间都进一步降低, 为0.11%和0.06 s. 自适应J和Dp协调控制时, 超调量和调节时间分别为0.10%和0.06 s. 综上分析, 在孤岛模式和并网模式下, 提出的自适应J和Dp协调控制算法都能使VSG的频率和输出有功更快恢复稳定, 提高系统运行的可靠性. 在VSG控制结构中加入基于LSTM的频率预测环节, 预测系统受扰动后频率的最低值或最高值. 利用频率的预测值, 在保证系统正常运行的同时, 使逆变器的转动惯量系数和阻尼系数拥有更大的整定范围. 在参数取值范围扩大的基础上, 利用逆变器参数实时可变的特点, 提出自适应转动惯量和阻尼系数协调控制策略. 通过Matlab/Simulink分别在孤岛和并网模式下进行仿真实验, 所提的自适应参数控制策略与固定参数策略相比, 在受到相同扰动下, 逆变器的频率和输出功率的超调量和调节时间都相应减少, 动态性能得到改善.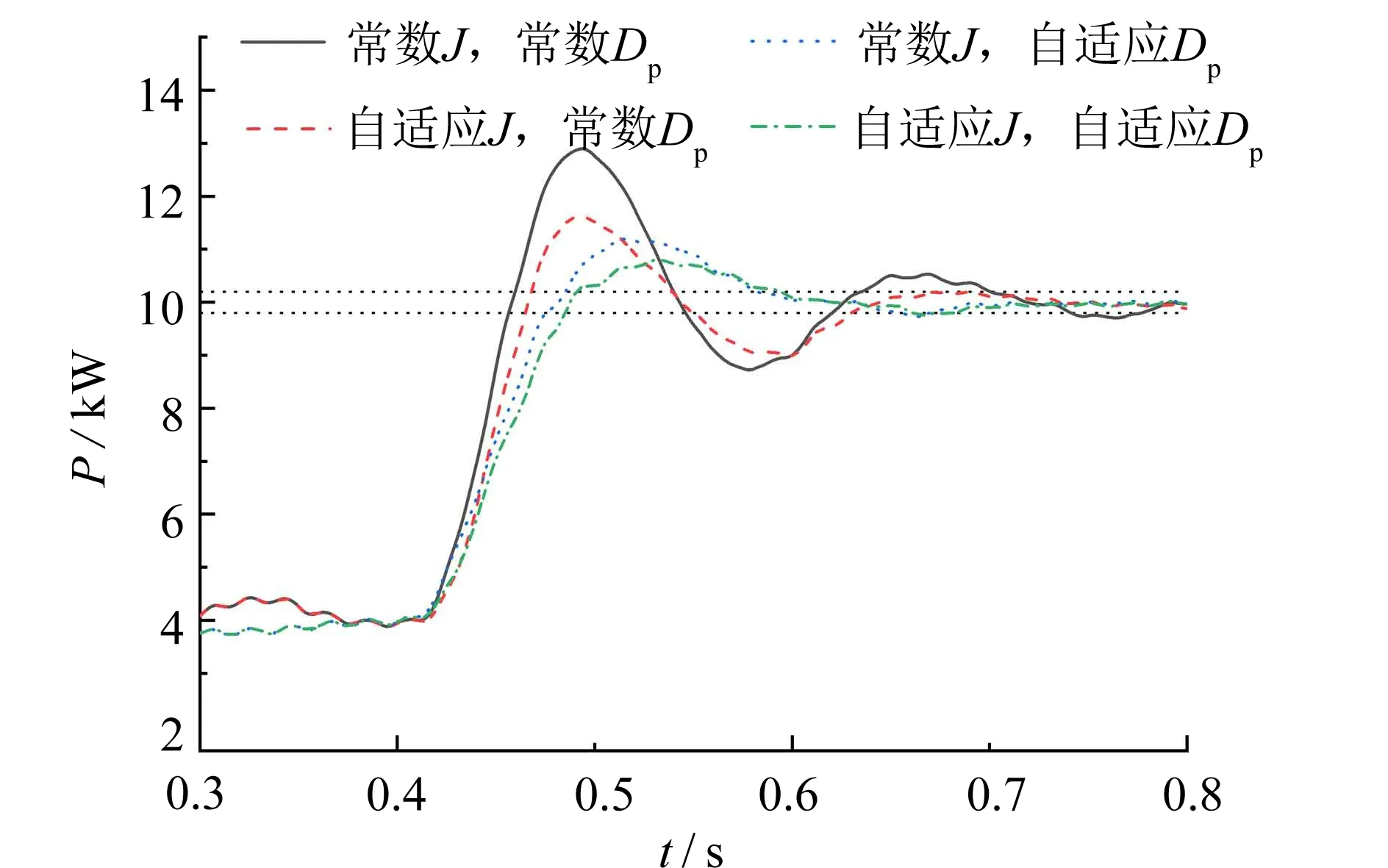
6 结语
