一种合作Markov决策系统

雷 莹，许道云

(贵州大学 计算机科学与技术学院，贵州 贵阳 550025)

1 概 述

在机器学习中，依据学习方式不同可以分为三大类[1]：监督学习、无监督学习和强化学习。其中，强化学习[2-4](又称为增强学习)是一个重要的研究领域，其目的是学习环境状态到行动的映射，本质是自主学习并解决负责的决策问题。通过强化学习的方式，智能体[5]能够在探索和开发之间进行折中处理，进而寻找最优策略[6-7]并获得最大回报。Asmuth等人[8]将寻找最优策略的方法归纳为三类，第一类是基于贝叶斯的方法，第二类是间接选择的方法，第三类是近似效用的方法，其中第一类方法的设计理论较为完善，可用来解决随机决策问题。

在强化学习中，Markov决策过程系统[9-10](Markov decision process system，MDP)极其重要，从计算模型的演变过程看：Markov过程(Markov process)(也称为Markov系统，Markov process system，MP)是基础模型，引入奖励函数和执行行为，并以状态集到行为集的一个映射作为策略[11]，求解Markov决策问题。在给定策略π下，Markov决策系统退化到带奖励函数的Markov系统MDPπ。一旦策略π给定，带奖励函数的Markov系统的主要任务是演化生成在每一个状态下的期望收集到的奖励值。Markov决策系统MDPπ的主要目标是求一个最优策略π*，使得在此策略下，在Markov链上收集到的期望奖励值最大。

在通常的Markov决策系统中，形式上是一个智能体在学习演化的过程。然而，在实际中往往会遇到这样的两类问题：

第一类是多个智能体在同一个环境中共同完成一个目标任务。这类系统称为协同[12]或合作系统[13]。在这类系统中，智能个体单独执行策略行为，智能体之间相互配合、共同完成一个目标任务。其最优策略组合表现为智能体策略向量(或组)，奖励值体现为组合执行的社会综合价值。

第二类是多个智能体在同一个环境中相互制约完成各自的目标任务。这类系统称为对抗或博弈系统[14-15]。在这类系统中，智能个体单独执行策略行为，智能体之间相互制约或博弈，各自完成自己的目标任务。其最优策略表现为智能体策略向量(或组)，奖励值体现为自身执行的奖励价值。文献[16]提出了多智能体非零和MDPs(Markov decision processes)对策的增强学习模型和算法，并通过预测对手的策略模型来修正自己的策略。

为方便起见，文中仅考虑两个智能体的联合Markov决策系统(CMDP)，这样的系统适用于两个智能体之间合作(或对抗)决策的演化学习系统。文中引入了联合Markov决策系统的形式定义，在此形式系统中，两个智能体(Alice和Bob)交替依据自己的策略执行行为动作，在给定策略对的Markov系统(带奖励函数)中演化学习，系统求优是针对策略求优。

2 Markov决策系统的进化过程

本节介绍从Markov系统模型到Markov决策系统的演化过程。

2.1 Markov系统

设S为一个有穷状态集(含有n个状态)，一个序对构成一个有限Markov系统，其中对每一个s∈S，定义一个概率分布Ts:S→[0,1]，Ts(s')表示由状态s转移到状态s'的概率。

通常，将概率转移函数T写成如下形式：

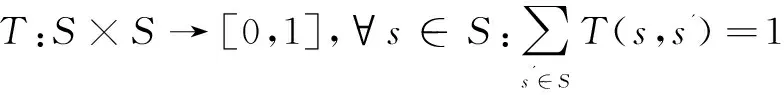
(1)

由一个Markov系统，可以规定一个Markov链：X0,X1,…,Xt,Xt+1,…，它是状态集S上的一个随机变量序列，满足如下条件：

Pr[Xt+1=st+1|X0=s0,X1=s1,…,Xt=st]=

Pr[Xt+1=st+1|Xt=st]=T(st,st+1)

(2)

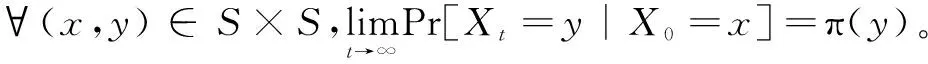
πP=π

其中：

π=(π(s1),π(s2),…,π(sn))

P=(pi,j),pi,j=T(si,sj)

2.2 带状态转移奖励的Markov系统

设S={s1,s2,…,sn}，函数T可由概率转移矩阵P=(pi,j)n×n决定。进一步，引入一个奖励函数R:S×S→(实数集)，R(s,s')表示由状态s转移到状态s'所获得的奖励值。类似地，函数R写成一个n阶方阵R=(ri,j)n×n，并将最大值记为Rmax。

递归定义一个(向后)期望收集到的奖励值：

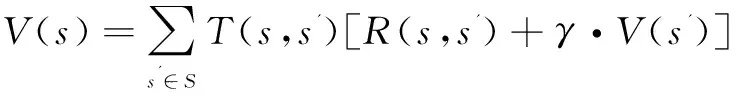
(3)

其中，0<γ<1称为折扣因子，以保证一个无穷级数收敛。式(3)表明，状态s为初始状态，在Markov链X0,X1,…,Xt,Xt+1,…上得到的奖励值。在式(3)中，项R(s,s')+γ·V(s')表明：从s开始，一步转移到s'获得的奖励值加上从s'开始收集的期望值打折。

为便于计算，可以将式(3)改写成如下方程：

i=1,2,…,n

(4)

其向量形式写成：

(5)

在迭代计算过程中，式(4)可以写成如下迭代公式：

(6)

其中，RT表示矩阵R的转置，diag(A)表示矩阵A对角线上元素构成的向量。

例1：概率矩阵P、奖励函数R、折扣因子取值如下。通过算例观察函数V的迭代计算收敛性。

γ=0.9

初始V0取为零向量(全取0)，则收敛状况如图1所示，其中横坐标表示迭代步数，纵坐标表示V(s)收敛值。

图1 V-函数收敛示意图

2.3 Markov决策系统

Markov决策系统是在带奖励函数的Markov系统中引入行为，并将奖励函数修改到行为执行步上。

奖励函数修改为：R:S×A×S→(实数集)。

引入策略概念，形如π:S→A的函数称为一个策略。π(s)=a代表在状态s下执行行为a。对于一个给定的策略π，可以将式(4)改写为：

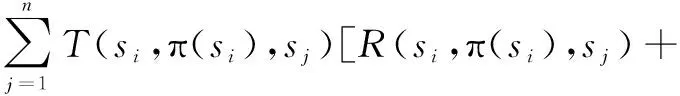
γ·Vπ(sj)],i=1,2,…,n

或

γ·Vπ(s')]

(7)

式(7)称为Bellman递归方程。它是一个不动点方程，V-函数作为一个不动点。可以看出：对于给定的策略，Markov决策系统是一个带奖励函数的Markov系统。

根据函数Vπ，将行为作为一个变量，可以诱导出另一种类型的奖励函数：Q-函数，如式(8)所示：

(8)

其中，Qπ(s,a)理解为：在指定策略π下，在s状态下执行行为a后期望收集到的奖励值。

Markov决策系统的主要目标是寻找一个最优策略π，使函数Vπ最大化。

3 Markov决策系统中求解最优策略方法

由上一节介绍，一个有限Markov决策系统是一个四元组，其中S是一个有穷的状态集，A是一个有穷的行为集，T:S×A×S→[0,1]是概率转移函数，R:S×A×S→R+是奖励函数。

对于策略π:S→A，由于表示期望收集奖励值的V-函数和Q-函数依赖π，并且由Vπ函数可以决定Qπ。因此，目标是寻找一个策略π，使函数Vπ最大化。

一个V-函数V*是最优的，如果对于任意策略π，对于任意状态s∈S，有V*(s)≥Vπ(s)。

一个策略π*是最优的，如果对于任意策略π，对于任意状态s∈S，有Vπ*(s)≥Vπ(s)。

显然，函数Vπ*是一个最优V-函数，其中，对于任意的状态s∈S，取V*(s)=Vπ*(s)。

一个自然的问题是：最优策略π*的存在性。其次，如果存在，如何计算得到π*。理论结果表明[18]：一个有限Markov决策系统的最优策略存在。

最优V-函数V*与最优策略π*有如下关系：

(1)如果已经得到最优函数V*，利用如下方法可得到最优策略π*：

γ·V*(s')]

(9)

(2)如果已经得到最优策略π*，利用如下方法可得到最优函数V*：

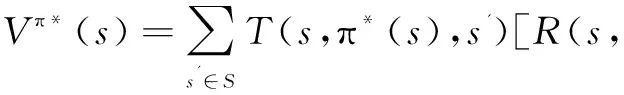
π*(s),s')+γ·Vπ*(s')]

(10)

式(9)和式(10)提供了一个交叉迭代，并求解得到最优策略π*和最优函数V*。

在具体计算过程中，用一个给定误差(ε>0)控制给定策略下Markov系统演化计算的停机条件，其计算方法及步骤如下：

第0步：初始化V-函数V0(可以随机取值，如取V0(s)=0(s∈S))

贪心计算一个策略π0：

γ·V0(s')]

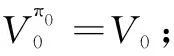
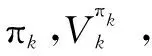
(1)Markov系统演化计算。

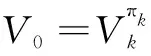
γ·Vm(s')]

即当πk给定后，用式(7)迭代计算，当‖Vm+1-Vm‖<ε时，定义(s)=Vm+1(s)(s∈S)。

(2)贪心计算。

算法终止条件：当πk+1=πk，终止计算，并定义最优策略π*=πk。

注：算法终止条件‖Vm+1-Vm‖<ε也可以用单点比较达到误差条件：|Vm+1(s)-Vm(s)|<ε。上述计算过程可以用图2表示。

图2 最优策略求解算法框架

例2：考虑一个Markov决策系统，其中S={s0,s1,s2},A={a0,a1}，概率转移函数T和奖励函数R分别如下：

折扣因子γ=0.95，误差控制取ε=0.000 1。

如图3所示，描述了所有策略下状态si对应的V(si)的收敛值。其中纵坐标表示V(s)收敛值。横坐标表示8(8=2×2×2)种策略，考虑有s0、s1、s2三个状态，且每个状态有a0、a1两种行为，因此横坐标上的每个数值对应一定的二进制码，进而表示相应的策略。表1为不同策略不同状态下的具体值。

图3 不同策略下的V-函数比较

表1 不同策略的具体值

实际计算中，最优策略可以由“迭代+演化”过程得到。此例中得到的最优策略下的概率转移矩阵P和奖励函数R分别为：

4 联合Markov决策过程系统(CMDPs)

本节引入两个智能体在同一个Markov决策过程中运行的联合形式系统。

4.1 两个Markov系统的乘积系统

设A=(ai,j)n×n,B=(bi,j)m×m为两个矩阵，矩阵A与B的张积定义为：A⊗B=(ai,jB)。

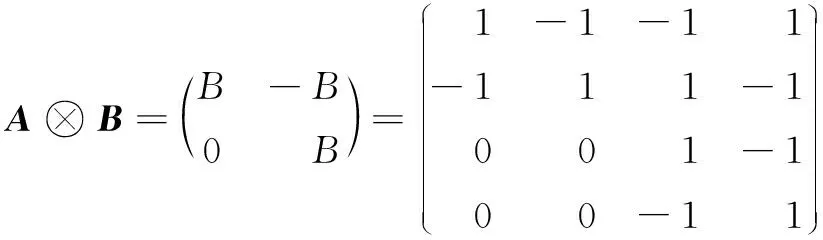
容易验证：如果P1,P2均为概率矩阵(不一定同阶)，则P1⊗P2也为概率矩阵。

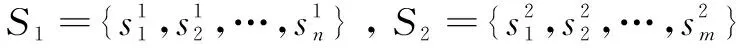
可分离的Markov系统：设(S,P)为一个Markov系统，如果它可以表示成两个Markov系统的积系统，则称(S,P)是可分离的。

4.2 两个智能体参与的联合Markov决策系统

现在考虑：在同一个系统中，具有两个智能体Agent0,Agent1(Alice和Bob)分别执行各自的行为动作，以合作方式完成目标任务。对于“合作”类型：两者协同完成同一个目标；对于“对抗”类型：两者之间相互制约(如：博弈)各自完成自己的目标任务。

形式上，这样的系统为如下元组：

其中，

S为一个有穷状态集；

A为一个行为动作集；

Ti为Agenti的概率转移函数(i=0,1)，定义为：

Ti:S×S×A×S×A→[0,1]。

直观上，T0(s1,s2,a,s',a')表示：“当Agent0,Agent1处于状态对(s1,s2)时，执行行为动作a后，Agent0转移到状态s'，合作者(或对抗方)Agent1响应执行行为a'”的概率。

Ri为Agenti的奖励函数(i=0,1)，定义为：

Ri:S×S×A×S×A→(实数集)

直观上，R0(s1,s2,a,s',a')表示：“当Agent0,Agent1处于状态对(s1,s2)时，Agent0执行行为动作a后，Agent0转移到状态s'，合作者(或对抗方)Agent1响应执行行为a'”时，Agent0获取的奖励值。

5 联合Markov决策系统策略迭代方法

文中仅考虑两个智能体合作执行的联合Markov决策系统。

形式上，两个智能体Agent0,Agent1对应两个V-函数：Vi:S×S→(i=0,1)。在联合形式下，用社会价值描述联合V-函数V:S×S→。形式上定义为：

V(s,s')=αV0(s,s')+(1-α)V1(s,s'),0<α<1

其中，参数α称为平衡参数。

策略函数定义为：πi:S×S→A(i=0,1)。将πi(s,s')=a理解为：当Agenti处于s状态，并观察到Agent1-i处于状态s'时，执行动作a。

对于给定的策略对(π0,π1)，演化联合Markov系统CMDP(π0,π1)得到一个稳定的V-函数，其迭代方程为：

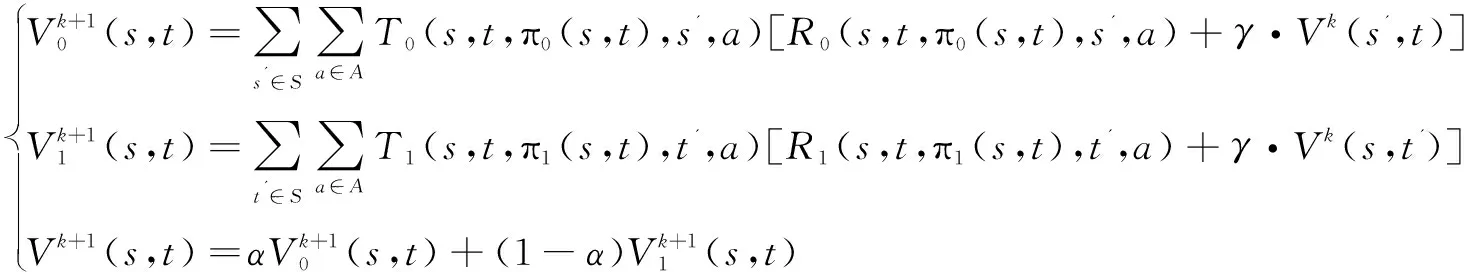
(11)

请注意：在式(11)中，带打折因子的倍乘项是基于S上的边缘分布求期望值：

其中，视s,t固定。

(12)

6 合作类型最优策略对的求解算法

第0步：给定误差参数ε以及平衡参数α；

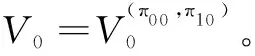
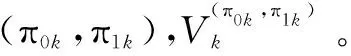
(1)Markov系统演化计算。

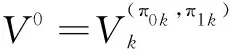
[R0(s,t,π0(s,t),s',a)+γ·Vm(s',t)]

[R1(s,t,π1(s,t),t',a)+γ·Vm(s,t')]

当‖Vm+1-Vm‖<ε时，做如下定义：

(2)贪心计算(π0,k+1,π1,k+1)。

t')]

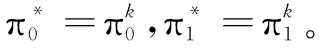
最终，Vm+1为最优V-函数，(π0,k+1,π1,k+1)为最优策略对。

7 结束语