针对STAP雷达的分布式投散射伪杂波干扰方法
2020-12-24张剑云周青松
王 坤,张剑云,周青松
(国防科技大学电子对抗学院,安徽 合肥 230037)
0 引言
空时自适应处理(space-time adaptive processing, STAP)技术因其出色的杂波抑制能力在机载雷达中被广泛应用[1-2]。近年来,在电子对抗领域,STAP雷达对抗技术引起了人们广泛的兴趣,研究人员提出了很多种干扰方法。这些干扰方法根据干扰路径的不同可以分为直接路径干扰和多路径干扰。
传统的直接路径干扰,如频移假目标干扰[3],间歇采样转发干扰[4],延迟转发干扰[5],卷积调制干扰[6]等均是对截获的STAP雷达信号进行调制后延时直接转发给STAP雷达,在不同距离门或不同多普勒通道形成若干假目标,但干扰维度单一,假目标与真实目标在同一方位上。
针对干扰维度单一的问题,文献[7—8]提出了投散射式伪杂波干扰这种多路径干扰方法。该方法将截获的STAP雷达信号调制后延时投射至地面,经地物散射至雷达,产生与杂波类似的具有空时二维耦合性质的干扰信号;经STAP处理后形成一个伪杂波凹口,通过改变调制和延时参数移动凹口位置以覆盖目标,使STAP雷达在滤除干扰信号的同时也将目标滤除,从而达到干扰效果。该办法利用了STAP的性质,克服了直接路径干扰信号的单维性,具有较大的研究价值,但对先验信息准确性要求较高,需要知道目标的准确距离、方位和多普勒频率。
本文针对投散射式伪杂波干扰需要精确的目标先验信息才能有效实施的这一不足,提出一种针对STAP雷达的分布式投散射伪杂波干扰,降低对目标先验信息精确性的要求。
1 投散射伪杂波干扰基本原理
投散射式伪杂波干扰通过运动平台上的干扰机向地面投射干扰信号,利用地物散射特性和雷达、干扰机、地面运动特性产生类似杂波的与STAP处理器信号空时二维矢量特性一致的干扰信号[7-8],经STAP处理器处理后产生一条与杂波凹口类似的伪杂波凹口,通过控制频移和延时等参数可以改变伪杂波凹口的位置,当伪杂波凹口覆盖目标时,目标信号被STAP处理器滤除从而不被雷达准确检测。
1.1 信号模型
机载预警雷达A、干扰机J的几何配置如图1所示。雷达以速度vA沿x轴方向飞行,距地面高度为HA,与干扰机的距离为r0,与地面散射点P的距离为r1。干扰机以速度vJ飞行,飞行方向与x轴夹角为δj,距地面高度为HJ,与地面散射点P的距离为r2。

图1 雷达和干扰机几何配置图Fig.1 Geometric configuration of radar and jammer
1.1.1干扰机接收到的雷达信号
假设雷达发射信号为:
st(t)=R[AtE(t)ejwct]
(1)
vr1=vAcosθrjcosφrj-vJcosθrj(cosφrj-δJ)
(2)
干扰机接收到的雷达信号为:
sjr(t)=R[AjE(t-τ(t))ejwc(t-τ(t))]
(3)
其中,
(4)
可知相对运动造成的多普勒频移为:
(5)
1.1.2雷达接收到的干扰信号
干扰机将接收到的雷达信号调制和延时后向地面投射,经地面散射后由雷达主瓣进入雷达形成干扰信号。调制和延时产生的多普勒频移为fj。由图1可知,散射块P到雷达、干扰机的距离和R2w=r1+r2是随时间变化的,不妨设t=0时,R2w=R0。在t时刻,干扰机接收到的信号是雷达在t-τ(t)时刻发射的,此时有:
R2w[t-τ(t)]=R0-(vAcosφricosθri-
vJcos(φrj-δj)cosθji)(t-τ(t))
(6)
可以解出:
(7)
其中,
vr2=vAcosφricosθri-vJcos(φrj-δj)cosθji
(8)
雷达、散射块P和干扰机相对位置变化产生的多普勒频移为:
(9)
经杂波块P散射产生的干扰信号总的多普勒频移为:
fdi=fd1+fd2+fj
(10)
雷达采用线性侧视阵列,N个阵元沿x轴分布,脉冲数为M,则干扰机产生的单一伪杂波模块的时间相位项和空间相位项分别为:
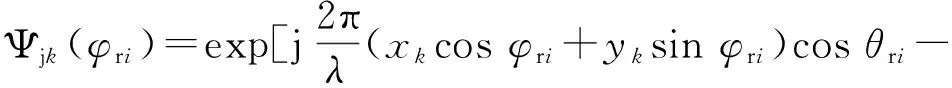
(11)
通过引入传感器方向图D(φri),发射方向图G(φri,m),地面反射率L(φri),那么在第m个时刻第k个传感器对于一个距离单元,可以得到总的干扰信号模块更精确的模型:
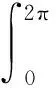
(12)
1.2 干扰信号性质分析
由式(10)可知伪杂波块的多普勒频移fdi由三部分组成。fd1由截取雷达信号时干扰机、雷达相对位置和速度决定。fd2与散射块P的位置有关,由式(8)、式(9)可知fd2具有方位依从性。fj由调制和延时产生,通过改变fj大小可以控制fdi。由于fd2的方位依从性,伪杂波干扰的功率谱与杂波的功率谱类似,具有空时二维性质,如图2所示。

图2 投散射干扰条件下的杂波谱Fig.2 The clutter spectrum under scattered jamming
1.3 投散射伪杂波干扰原理
雷达在接收到伪杂波干扰后,STAP处理器像处理杂波一样处理伪杂波,干扰前后的STAP改善因子对比如图3所示。从图中可以看到对干扰后的信号,STAP处理器不仅产生一个杂波凹口以滤除杂波,还产生了一个伪杂波凹口以滤除伪杂波。
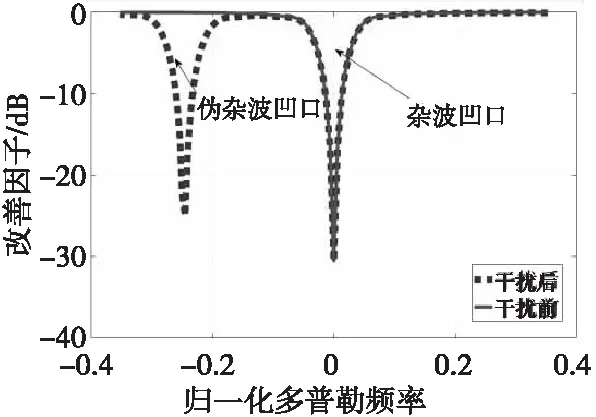
图3 干扰前后改善因子对比Fig.3 Comparison of improvement factors before and after jamming
通过调整fj可以改变伪杂波谱在空时二维平面中的位置,进而改变STAP处理器所产生的伪杂波凹口位置,当伪杂波凹口覆盖目标时,STAP处理器在滤除伪杂波的同时也将目标滤除。图4是干扰前的最优响应,目标处获得最大响应,目标被雷达准确检测。图5和图6是干扰后的响应。图5中伪杂波凹口覆盖了目标,目标处的响应极低,使雷达不能检测到目标从而达到干扰效果。图6中伪杂波凹口未能覆盖目标,目标处仍然能获得最大响应,目标被雷达准确检测,不能达到干扰效果。

图4 干扰前最优响应Fig.4 Optimal response before jamming
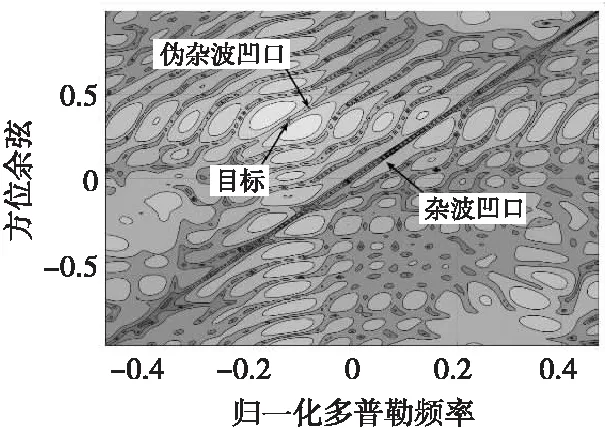
图5 伪杂波凹口覆盖目标时的最优响应Fig.5 Optimal response before jamming

图6 伪杂波凹口未覆盖目标时的最优响应Fig.6 Optimal response when the fake clutter notch does not cover the target
2 分布式投散射伪杂波干扰
由上一章内容可知,投散射伪杂波干扰要达到干扰效果需要使伪杂波凹口覆盖目标,需要有准确的先验信息,知道目标的方位余弦和归一化多普勒频率。显然伪杂波凹口越宽越容易覆盖目标,对目标先验信息的准确性要求越低。为明确起见,我们将伪杂波凹口宽度定义为改善因子为-10 dB处伪杂波凹口占据的归一化多普勒频率宽度。对于单个伪杂波凹口,其宽度主要由两个因素决定:一是伪杂波谱的宽度,伪杂波凹口本质上是对伪杂波谱求逆,伪杂波谱越宽,为了滤除它而形成的伪杂波凹口就越宽;二是STAP雷达留给信号的自由度,即系统自由度(阵元数N与脉冲数M的乘积)减去杂波和干扰占据的自由度。图7是不同系统自由度的STAP雷达在相同条件下的改善因子,可以看到系统自由度越大,留给信号的自由度就越大,STAP雷达的性能越好,所形成的杂波凹口和伪杂波凹口越窄,从而对目标先验信息的精确性要求越高。

图7 不同自由度STAP雷达的改善因子Fig.7 Improvement factors of STAP radar with different degrees of freedom
为了展宽伪杂波凹口,降低对先验信息的精确性要求,本文提出一种分布式投散射伪杂波干扰方法。采用多部干扰机同时进行干扰,针对影响伪杂波宽度的两个因素,从两个方面展宽伪杂波凹口:一是通过控制各干扰机的fj使它们产生的伪杂波谱叠加从而在目标附近形成一个较宽的伪杂波谱;二是多部干扰机会占用STAP更多的系统自由度,使留给信号的自由度减少。
2.1 分布式投散射伪杂波干扰下的杂波谱
分布式投散射伪杂波干扰下雷达、目标和干扰机的几何配置如图8所示。STAP雷达主瓣对准目标,5部干扰机对雷达主瓣照射的地面区域投散干扰信号,每部干扰机产生具有空时二维特性的伪杂波干扰信号。由式(8)和式(9)可知,伪杂波干扰在空时二维平面上的斜率为vAcosθri/λ,当HA与r1相比很小时,cosθri约为1,从而斜率约为vA/λ,故当干扰机与雷达的距离使得r1足够大时,干扰机本身的方位角取值对干扰效果影响很小,因此分布式投散射伪杂波干扰中各干扰机的空间配置可以随机选择。由式(11)可知,当各干扰机的fdi不同时,产生的干扰信号的空时导向矢量是线性无关的,各干扰机的伪杂波谱可以叠加。从图7可知N=18,M=16时,伪杂波凹口宽度约为0.03归一化多普勒频率,分别控制每部干扰机的fj,使它们产生的fdi间隔0.03归一化多普勒频率,伪杂波谱合成为一个很宽的伪杂波脊。图9和图10分别是3部干扰机和5部干扰机进行投散射伪杂波干扰时的杂波谱。

图8 分布式干扰几何配置示意图Fig.8 Schematic diagram of distributed jamming geometry configuration

图9 3部干扰机投散射干扰条件下杂波谱Fig.9 The clutter spectrum under scattered jamming by 3 jammers

图10 5部干扰机投散射干扰条件下杂波谱Fig.10 The clutter spectrum under scattered jamming by 5 jammers
结合图2可知,随着干扰机数量的增多,伪杂波脊越来越宽,可覆盖的空时二维区域越大,STAP雷达对伪杂波谱求逆形成的伪杂波凹口越宽。
2.2 分布式投散射伪杂波干扰的特征谱
文献[11]引入了对空时协方差矩阵特征谱的分析。干扰(包含杂波)加噪声的协方差矩阵的特征值分布表明了干扰和杂波对矢量空间的占据情况,其特征值数目指示了干扰场景的自由度。要想抑制干扰,STAP处理器至少需要这个数目的自由度。文献[12]发现了侧视线阵的空时协方差矩阵特征值数的规则:
(13)
式(13)中,γ=2vAT/d,T为脉冲重复间隔,d为阵元间距,int表示下一个整数。文献[13]对式(13)进行了证明。文献[7]给出了侧视线阵投散射伪杂波干扰信号空时协方差矩阵的特征值数规律:
(14)
式(14)中,βJ=fdi/(dcosφricosθri),fdi由式(10)给出。m部干扰机同时进行投散射伪杂波干扰时,杂波加干扰协方差矩阵的特征值数为:
(15)
图11是N=18,M=16,fdi间隔0.03归一化多普勒频率,m取不同值时的杂波加干扰协方差矩阵特征值数的比较。m越大,杂波加干扰占用的自由度越多,留给信号的自由度越小,STAP处理器的性能越差。

图11 不同数目干扰机条件下的空时协方差矩阵特征谱(N=18,M=16)Fig.11 Characteristic spectrum of space-time covariance matrix under different number of jammers
3 仿真结果与分析
仿真实验设置:STAP雷达飞行高度为10 000 m,雷达平台飞行速度为150 m/s,机载雷达载波频率380 MHz ,脉冲重复频率为800 Hz,天线阵元个数为N=18,间隔为半波长,侧视阵观察,脉冲积累数M=16,杂波噪声比CNR=30,信噪比SNR=0,干噪比JNR=20。目标飞行高度为3 000 m,方位角为70°,距离雷达80 km,对雷达的径向速度为-40 m/s。干扰机速度均为50 m/s,偏航角均为20°,位置参数见表1。单部干扰机时为干扰机1,3部干扰机时为干扰机1、2、3。为了进行定量比较,目标的参数不变,经计算目标的真实归一化多普勒频率为-0.122,方位余弦为0.342。要求干扰后目标响应下降10 dB以上。
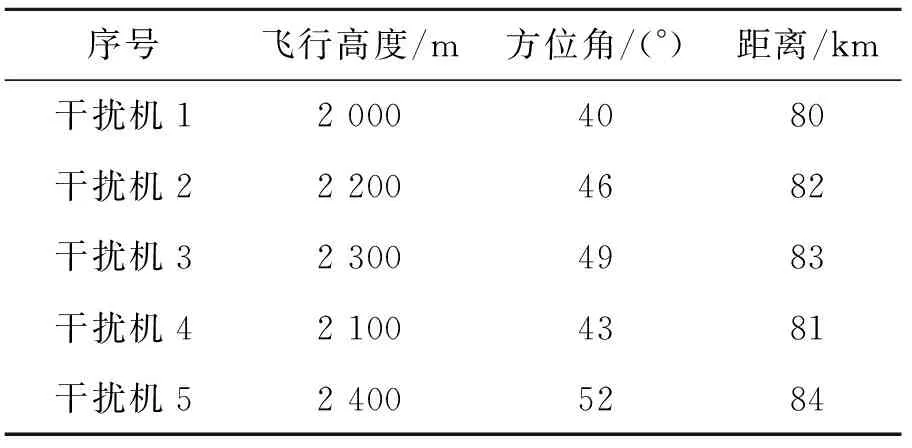
表1 干扰机位置参数Tab.1 Position parameters of the jammers
3.1 先验信息误差对投散射伪杂波干扰效果的影响
图12是单部干扰机投散射伪杂波干扰下STAP雷达的最优响应。图12(a)中,在无干扰的情况下,目标获得最大响应。图12(b)中,在先验信息准确的情况下,伪杂波干扰获得最佳效果,目标响应下降了24.9 dB。从图12(c)—图12(f)可以看出,随着先验信息误差增大,干扰效果越来越差,当先验信息误差大于0.015归一化多普勒频率时,目标响应已经高于-10 dB,不能满足干扰要求。仿真结果验证了单部干扰机投散射伪杂波干扰对先验信息准确性有较高的要求。

图12 先验信息误差对投散射伪杂波干扰效果的影响Fig.12 Influence of prior information error on scattered fake clutter jamming effect
3.2 分布式投散射伪杂波干扰下STAP雷达的改善因子
不同数目干扰机伪杂波干扰条件下STAP处理器的改善因子对比如图13所示。图13(a)中通过调整各干扰机fj使它们的伪杂波凹口间隔0.03归一化多普勒频率,随着干扰机数目的增加,合成的伪杂波凹口越来越深,宽度越来越大;另外可以看到杂波凹口并没有如预想的那样展宽,这主要是因为N=18,M=16,系统的自由度非常大,受到分布式干扰后系统有足够的自由度留给信号,STAP处理器的杂波抑制性能没有恶化,杂波凹口没有展宽。图13(b)中调整各干扰使形成的伪杂波间隔0.05归一化多普勒频率,则可以形成更宽的伪杂波凹口,但深度不如图13(a),此时伪杂波干扰占用的自由度比图13(a)的情况要大,因此杂波凹口较图13(a)有所展宽。图13(c)中调整各干扰 使形成的伪杂波间隔0.1归一化多普勒频率,此时由于伪杂波间隔过大,各凹口没有相连。目标若在凹口之间,仍能获得较大响应,达不到干扰效果,所以伪杂波间隔并不是越大越好。

图13 不同数目干扰机干扰下STAP处理器改善因子对比(N=18,M=16)Fig.13 Comparison of improvement factors of STAP processors with different number of jammers(N=18,M=16)
如果取N=10,M=10,其他条件均不变,则STAP改善因子对比如图14所示,随着伪杂波之间间隔加大,干扰信号之间的不相关性变大,干扰占据的自由度增大,由于系统本身自由度不高,可以看到随着干扰机数目增多,杂波凹口越来越宽,STAP处理器杂波抑制性能恶化。因此,对于小自由度系统,可以适当增加伪杂波间隔。

图14 不同数目干扰机干扰下STAP处理器改善因子对比(N=10,M=10)Fig.14 Comparison of improvement factors of STAP processors with different number of jammers(N=10,M=10)
3.3 先验信息误差对分布式投散射伪杂波干扰效果的影响
图15是使用3部干扰机进行投散射伪杂波干扰后STAP处理器的最优响应。图15(a)—图15(c)伪杂波的间隔为0.03归一化多普勒频率,此时整个伪杂波凹口宽度约为0.1归一化多普勒频率,允许的目标先验信息误差为0.05归一化多普勒频率。图15(d)—图15(f)伪杂波的间隔为0.05归一化多普勒频率,此时整个伪杂波凹口宽度约为0.15归一化多普勒频率,允许的目标先验信息误差为0.075归一化多普勒频率。
图16是使用5部干扰机进行投散射伪杂波干扰后STAP处理器的最优响应。图16(a)—图16(c)伪杂波的间隔为0.03归一化多普勒频率,此时整个伪杂波凹口宽度约为0.15归一化多普勒频率,允许的目标先验信息误差为0.075归一化多普勒频率。图16(d)—图16(f)伪杂波的间隔为0.05归一化多普勒频率,此时整个伪杂波凹口宽度约为0.25归一化多普勒频率,允许的目标先验信息误差为0.125归一化多普勒频率。
对比图12和图15、图16可以看到,分布式投散射伪杂波干扰展宽了伪杂波凹口,降低了对目标先验信息准确度的要求。

图15 先验信息误差对分布式投散射伪杂波干扰效果的影响(3部干扰机)Fig.15 Influence of prior information error on distributed scattered fake clutter jamming effect

图16 先验信息误差对投散射伪杂波干扰效果的影响(5部干扰机)Fig.16 Influence of prior information error on distributed scattered fake clutter jamming effect
4 结论
本文提出了一种针对STAP雷达的分布式投散射伪杂波干扰方法。该方法采用多部干扰机同时向地面投射信号,利用地物散射形成具有空时二维耦合性质的干扰信号,通过改变调制参数合理选择频率间隔,合成出很宽的伪杂波谱并占据了更多的自由度,经STAP处理后形成可以覆盖更多多普勒通道和方位的伪杂波凹口,使STAP雷达在滤除伪杂波的同时滤除目标,从而达到干扰效果。仿真实验结果表明,相比于单部干扰机投散射式伪杂波干扰,该方法展宽了伪杂波凹口,更容易覆盖目标,降低了对目标先验信息精确性的要求。本文所提干扰方法针对的是传统的STAP雷达,考虑到STAP技术在新体制雷达(如MIMO雷达)中的应用,特别是引入稀疏恢复技术的MIMO-STAP具有很强的干扰抑制能力[14-15],如何有效对抗这些新技术需要进一步研究。
