舰载光电侦察设备视频测距实时修正方法
2020-12-24徐亚飞
徐亚飞
(华中光电技术研究所武汉光电国家研究中心,湖北 武汉 430073)
0 引言
光电侦察设备主要由电视、红外传感器及伺服系统等组成,光电侦察设备具有图像清晰直观,可昼夜工作,不受电子干扰,环境适应性好等优点,大量列装于港口、岛礁与各型舰船等平台[1]。光电侦察设备一般不配备激光测距仪,无法获取目标实时距离信息。光电侦察设备传统的工作方式是利用设备架设高度、设备俯仰角度信息,通过直角三角形关系来计算目标距离[2]。这种距离估算方式受设备安装条件影响较大,设备安装平面水平度高、平面高度较高时,估算的距离准确度高,但一般情况下设备安装的环境很难满足上述要求[3]。随着计算机图像处理、机器视觉技术的发展,陆续出现了多种目标距离估算方法,如基于单目视觉[4]、双目视觉的实时测距方法[5],基于目标可见光特性的测距方法[6],多探测器数据集成的测距方法等[7],均未提及在舰船等动平台测距产生误差的问题。本文采用基于目标提取的视频距离估算方法,当设备安装在港口等静平台上时,采用该测距方法估算速度快且精度较高,但当设备装在舰船等动平台上后,由于舰船摇摆导致获取目标像素高度不稳定,从而导致获取目标估算距离也不稳定。本文针对此问题,提出了舰载光电侦察设备视频测距实时修正方法。
1 视频测距原理及缺陷
1.1 视频测距原理
视频测距原理示意图如图1所示。

图1 视频测距原理示意图Fig.1 Video ranging principle
在理想光学系统中,处于同一介质中物与像,它们的焦距相等。如图1中物方焦距与像方焦距相等,用f′表示。图1中AB=H表示物高,AF=D′,A′B′=h,表示像高,PF=f′。
(1)
式(1)中,D为目标近似距离,H为目标实际高度,h为目标相高,f′为焦距。
当目标距离较远时,在视频距离估算中要考虑因地球曲率遮挡目标引起的误差,在估算过程中需要对地球曲率遮挡进行修正,原理如图2所示。
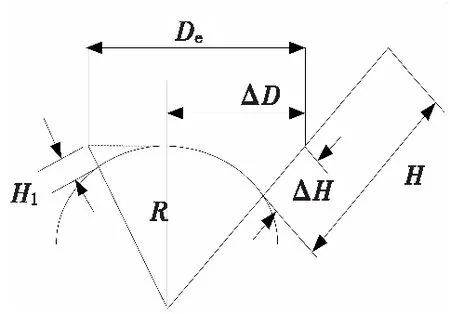
图2 地球视见距离关系图Fig.2 Earth seeing distance relationship
海上目标视见距离的经验公式为:
(2)
式(2)中,H1为光电侦察设备头部瞄准线海拔高度,ΔH为地球曲率遮挡目标高度。
根据式(2)可得由ΔH所引起的距离误差为:
(3)
式(3)中,D′为目标全部呈现时,估算出的目标的距离,即按测距式(1)计算的近似距离。当目标因地球曲率被部分遮挡时,按式(1)计算的名义距离总是偏大,因此实际距离应为:
(4)
海上光电侦察设备采用视频测距方法估算距离时,采用式(4)进行计算。
上述距离推导公式中,光电侦察设备的架设高度H1、传感器当前的焦距值f′可以直接获取,被测目标的实际高度H可由操作人员根据经验给定。因此,只要求出目标像高就可以求得目标距离,且目标像高的精度直接影响着目标距离的准确性。
为了准确地获取提取目标的像高,采取空间域的拉普拉斯变换对图像进行边缘增强,同时为了减少噪声对提取精度的影响,采用了中值滤波对图像进行预处理[8-9]。边缘增强与中值滤波本文中不再详细阐述。
1.2 舰船平台下视频测距存在的问题
当光电侦察设备安装在港口等固定平台上时,采用该测距方法距离估算速度快且精度较高,但当光电侦察设备装在舰船等动平台上后,由于舰船摇摆导致获取目标像素高度与实际像素高度有误差,导致估算的目标距离产生误差[10],因此在使用上述方法进行距离估算时,需要进行实时修正,即消除船体摇摆对获取像素高度的影响。
2 视频测距实时修正方法
通过试验观察发现,舰载光电侦察设备获取的视频图像由于舰船的摇摆而晃动。通过进一步分析可知,在设备跟踪锁定目标时,目标视频图像绕着一个中心点左右旋转导致获取的目标像素高度值跳动,为了修正目标像高,需获取目标图像绕中心左右旋转的像旋角θ。因此实时修正方法采用获取像旋角θ并将其消除,得到修正后的像高取代原像高的方式进行距离估算。求取像旋角θ的具体方法步骤如下所述。
2.1 大地坐标系下物方矢量
首先应获得大地坐标系下物方矢量,其示意图如图3所示。

图3 大地坐标系下物方矢量示意图Fig.3 The object vector in the geodetic coordinate system
确定大地坐标系(OXYZ)下,物方矢量为:

2.2 甲板坐标系下物方矢量
船体纵摇角为P和横摇角R示意图如图4所示,纵摇角P是船绕Y′轴旋转的角度,横摇角R是船绕X′轴旋转的角度。
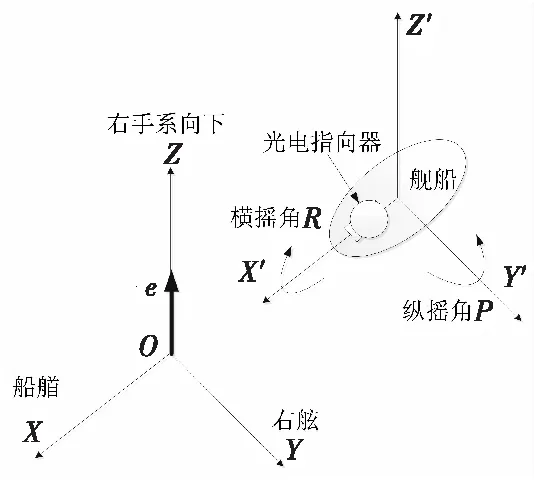
图 4 甲板坐标系下船体纵摇角P和横摇角R示意图Fig.4 Hull pitch angle P and roll angle R in deck coordinate system
甲板坐标系(OX′Y′Z′)下,舰船纵摇角为P、横摇角为R,艏摇角为船绕Z′旋转的角度,一般为0。则物方在大地坐标系下的矢量e,转换为甲板坐标系下的矢量为e′,他们的转换关系如式(5):
e′=M·e
(5)

(6)
M是大地坐标系转换为甲板坐标系的转换矩阵。
最终计算得:

(7)
2.3 指向器坐标系下物方矢量
指向器安装在舰船甲板上,如图5所示。指向器外环方位角q是指向器绕Z″转动的角度。俯仰角p是指向器绕Y″转动的角度(指向器指向舰艏时方位为0°。q沿Z″轴逆时针转动为正,p沿着Y″轴逆时针转动为正),由于探测器安装在指向器内框架俯仰包上,探测器坐标系(OX″Y″Z″)与指向器坐标系一致,从舰船甲板坐标系到探测器坐标系的转换矩阵N为:

图5 探测器坐标系下像方矢量示意图Fig.5 Image side vector in detector coordinate system
(8)
所以在探测器坐标系(OX″Y″Z″)下,像方矢量e转换为E:
(9)
则可以获得需要消除的像旋角为:
(10)
则修正后的像素高度为:
(11)
将修正后的像素高度h′替代视频距离估算公式中的像高h进行运算,即可获得修正后的距离估算值。
3 实验验证
在舰船纵摇8°、横摇8°、摇摆周期12 s的情况下采用未修正的距离估算方法,修正后的距离估算方法及激光测距方法(获取的距离值可认为是真值),对不同目标同时进行测距,获取了12组实验数据,如表1所示。
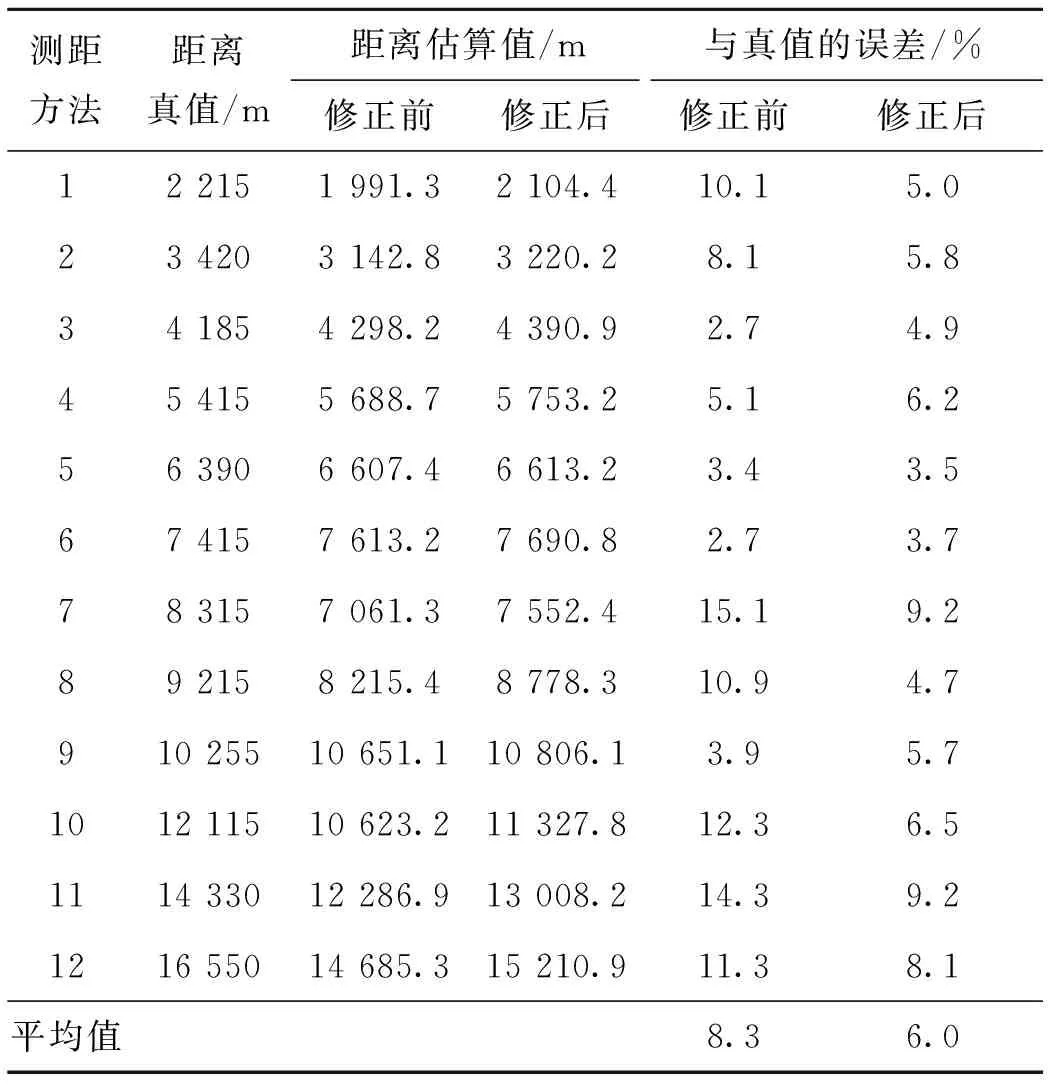
表1 实验结果对照表Tab.1 Comparison of experimental results
由表1可见,采用修正后距离估算方法测得的距离值与真值的误差大大减小,单次最大误差由15.1%减小到了9.2%,平均误差由8.3%减小到了6.0%。
4 结论
本文提出了舰载光电侦察设备视频测距实时修正方法。该方法以修正后的像素高度替代视频距离估算公式的原始像高,得到了稳定的视频估算距离。仿真实验结果表明,采用此修正方法很好地解决了由于船体摇摆导致的估算距离不准问题,使视频距离估算方法在舰载光电侦察设备中得到了很好地应用,提高了舰载光电侦察设备的整体性能。
