探讨高中数学抛物线的解题方法与技巧

赵冬梅

摘 要：数学作为一门重要学科，其中的抛物线知识在高考中占据较大比例，尤其是抛物线问题，其可以与其他数学知识进行充分结合，形成难度较大的综合题，如果一部分学生基础不够扎实，就不会解决这类题型。所以针对高中数学抛物线中相关的解题方法与技巧进行分析。

关键词：高中数学;抛物线;解题方法;具体技巧

抛物线的定义与性质，有关坐标轴交点、方向与几何结合的问题，一直是高考中的重难点，也是出错率比较高的一部分数学教学内容。为了使这部分课程教学取得更好的效果，本文重点对数学抛物线解题方法与技巧进行研究，据此展开讨论。解题方法的掌握是提升学生数学成绩的基础，我们在教学过程中要予以重视。

一、定义

若抛物线存在一个顶点，命名为F，且随之形成的定直线就被称为抛物线的准线，而点到准线之间的距离，则被称为焦准距。用字母p来进行表示，其中p>0。

抛物线既可以用参数进行表示，又可以以标准方程的形式呈现，这种呈现性质是由圓锥面以及其平行于某条母线的平面相截取得到。在相应条件下，抛物线本身也可以看作是二次函数的图象。

二、常见参数

抛物线的标准方程：

向右开口的方程表示为：y2=2px（p>0）;向左开口的方程表示为：y2=2px（p<0）;向上开口的方程表示为：y2=（p>0）;向下开口的方程表示为：y2=（p<0）。在二次函数中，公式的表示方法如下：y=ax2+bx+c（a不等于0）。

若a>0，则开口方向向上;若a<0，则开口方向向下。当a的绝对值逐渐增大时，那么二次函数图象的横纵坐标数值也就越大，而图象与y轴之间的夹角也就越小;当a的绝对值逐渐减小时，则其相应的函数图象的横纵坐标数值也就越小，而图象与y轴之间的夹角也就越大。

函数图象与x轴之间的交点情况，取决于Δ=b2-4ac的取值，若b2-4ac>0，则表达式y=ax2+bx+c的图象与x轴的交点个数为2个，若b2-4ac=0，则表达式y=ax2+bx+c的图象与x轴的交点数为1个，若b2-4ac<0，则表达式y=ax2+bx+c的图象与x轴不存在任何交点。

二次函数y=ax2+bx+c的对称轴x=-，a>0且b>0时或者a<0且b<0时，图象对称轴在原点左边，a>0且b<0时或者a<0或者b>0时，图象对称轴在原点右边。我们也可以用“左同右异”的口诀来帮助学生进行识记。

三、解题方法与技巧

例题1：存在动点M到F（8，0）的距离较之它到直线x+10=0的距离短2，求M点的运动轨迹方程式。

通过对题目的阅读和理解，可将动点M的坐标设为（x，y），由此可知，动点M到F（8，0）的距离可以由解得，由题目中的等量关系，我们可以分析出=x+10-2，通过化简法，我们可以将题目中的距离不等看作是距离相等，那么由抛物线的定义就可以求出方程。

解题过程：

前面已经设动点M的坐标为（x，y），按照题意可知，点M轨迹是F（8，0），是交点，因为=8，>0，所以p=16，又因为焦点F（8，0）在x轴正半轴上，所以综上所述，点M的轨迹方程为y2=32x.

解题经验和审题思维是学生在学习高中数学的过程中最需要具备的技能，学生既要充分掌握抛物线中的各项知识点，又要审好题目，对症下药进行解题。

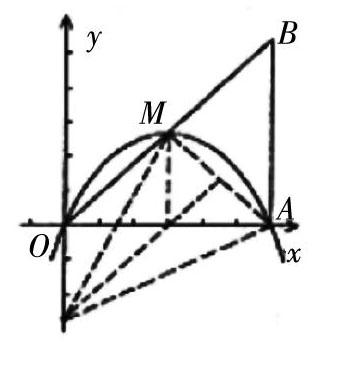
例题2：如下图所示，总面积18的等腰直角△OAB的三条边中，其中一条直角边OA在x轴上，二次函数：y=ax2+bx+c（a不等于0）的图象分别经过了原点、A点以及位于斜边OB上的终点M，根据以上条件需要求出该二次函数的具体解析方程式以及对称轴，应怎么解答。

解题过程：

因为S△OAB=18且△OAB为等腰直角三角形，所以OA=OB=6，又因为M是斜边OB的中点，因此，点A的坐标可以表示为（6，0），点M可以表示为（3，3）。

设y=ax2+bx+c（a不等于0）

得36a+6b+c=09a+3b+c=0c=0

解得

因此，该函数解析式可以表示为y=-x2+2x。

而对称轴则可用如下方程式来表示x=-=3。

分析：我们可以从上述求解过程中看出以下思路，其将抛物线与几何性质进行结合，难度并不是很高，学生只需要对相关知识内容有所理解就可以轻松解得结果，但是这一类题型也可以进一步展开。

如下题：根据上图所示，观察分析坐标轴上是否存在P点，满足ΔPMA中PA与PM相等的条件。如果存在，则求出P点的值，如不存在，则说明原因所在。

展开后，题目难度就有所加大，这时也需要学生对题目条件进行全面审查，否则在大题中如果出现条件遗漏就等于做无用功，解不出正确答案，所写内容也不得分。对于这一类型的题目，知己知彼才能有胜算，否则宁愿放弃。如果这类题型不能做到全部正确，基本等于在考场上浪费时间。

四、结语

由此可见，从数学课程教学的角度上来说，运用适当的方法是教学取得效果的关键因素。只有在正确的方法指导下，学生才能获得正确的结果，才会在成绩上体现出数学学习上的效果。

参考文献：

郭可欣.探讨高中数学抛物线的解题方法与技巧[J].课程教育研究，2017（11）：147-148.

编辑 冯志强