解读高中数学函数解题思路多元化的方法

摘 要：在高中数学教学过程中，函数一直以来都是重点内容，同时也是一大难点。教师在教学函数知识，尤其是解题教学时，学生的思维灵活性以及老师的教学方法都直接影响到了教学效果。而近些年，教学方法的改善以及教育理念的转变，使教学手段越来越多样化，而就函数解题教学来说，利用多元化的解题思路是化简知识难度、提高教学效率的有效方法。基于此，针对高中数学函数解题教学中思路的多元化进行分析，提出了相关的教学策略。

关键词：高中数学;函数知识;多元化;解题思路

近些年，新课改的进一步推进，使得生本理念成为高中教学的主导理念，要求在教学过程中以学生为中心，以培养学生各方面能力为目标，以创新性的教学方法为途径，进一步改善高中教学质量。而在教学高中函数知识过程中，函数例题的解题思路至今都是令学生和老师头疼的问题，学生很难找到正确的解题思路，即便掌握了解题方法，也无法融会贯通，对此多数老师也束手无策，不知如何引导。而通过多元化的解题思路，能够充分发散学生的思维，从而提高学生的思维灵活性，往往能够在解题中“另辟蹊径”。

一、通过图形结合法化简例题难度

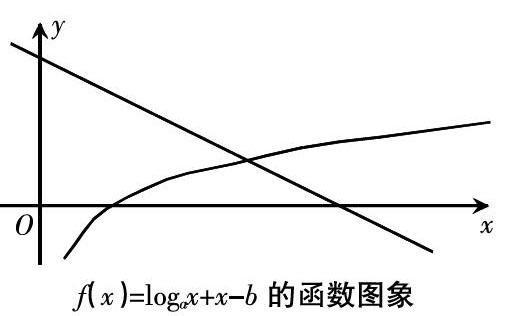
高中阶段的学生在理解能力和学习能力等方面已经较为成熟，而对函数知识感到困难和无从下手的主要原因是在理解方面仍然存在一些“障碍”，这些障碍可能是由于函数知识较为抽象，也可能是因为对知识的理解仍然不够透彻，或思维受到局限等。基于种种因素的影响，使得学生常常难以利用形象思维来理解函数知识，这也给知识的应用带来了阻碍。利用多元化的解题思路，应用图形结合法，则能够将原本抽象的知识和例题条件在坐标系中展现出来，从而有效降低例题的难度，帮助学生理解和解答。如例题“已知函数f（x）=logax+x-b，a>0，同时a≠1，那么求2

二、培养学生的思维创新能力

高中阶段的学生若想学好函数知识，必须要掌握大量的公式知识和概念知识，同时在解题方面也需要具备一定的思维能力。而解题教学便是培养学生思维创新能力的最好契机，多数学生面对一种函数题型时往往只会通过一种思路和方法来解答，虽然能得到答案，但不会灵活运用，对于为什么如此解答也一概不知，甚至无法根据解题思路进行逆反推理。这种情况下，学生常常完全找不到解答的思路，思维无法灵活发散，也无法实现创新，久而久之只能将知识丢在课堂。同时一些函数题的教学方法也存在不足，多数老师所教授的解题方法过于固态化，基本上相同类型的例题只讲一种解题方法，对于之后的相似题型也只是一句“这类题讲过”而带过，这种解题教学会导致学生思维僵化，对学生的学习极为不利。而多元化的解题思路则能有效改善这一境况，多元化的解题思路本身便是为了活跃学生的思维，引导学生创新思维，从而找到解题的规律，找到更多的解题方法。而在实际教学过程中，老师也需要灵活应用这一教学方法，如在“求f（x）=x+（x>0）的值域”过程中，便可以利用不同的解题思路和方法来引导学生，其一：随机选取两个<0的数a和b，之后进行代入，便能得到两个相减<0，相乘>0的数值。若a×b-1<0，那么导数a-b>0，因此函数在（0，1]中逐渐递减，若1

三、利用不同角度另辟蹊径

对于函数解题来说，思考的角度不同，解题方式也会不同，函数例题的不同解题方法殊途同归，而利用不同角度另辟蹊径对学生来说也是培养创新意识的一种手段。通过多元化的解题思路，利用一题多解的教学方法，让学生主动学会举一反三，而在解题期间，学生的思维能力和创新能力都能获得有效提高。如在函数题“求y=的函数值域”中，可以利用判别式法，根据x2+x+1>0得知，函数值的定义域为R，那么函数y=则能转变为（y-2）x2+（y+1）x+y-2=0。若y-2=0时，x∈R，当y-2≠0的情况下，始终会有实根的存在。所以Δ=（y+1）2-4（y-2）2≥0，且1≤y≤5且y≠2，那么函数的值域为[1，5]。一般来说，若函数中存在二次项，那么判别式法则能够发挥很好的效果，不过在应用判别式法來解答函数求解问题过程中，必须要保证系数大小能够准确判定，也就是要确定系数是否为0。

总之，在高中数学函数解题教学过程中，利用多元化的解题思路能够有效引导学生思维进行发散和创新。以目前高中数学教学状况来看，转变传统教学理念仍然是教学发展中必须要进行创新的，而解题思路多元化的方式也很好地迎合了现代学生的学习需求和现状，在函数教学中发挥着重要的作用。

参考文献：

[1]魏彦平.关于高中数学函数解题思路多元化的方法举例探索[J].学周刊，2018（22）：39-40.

[2]姜蕾.浅谈高中数学函数解题思路多元化的方法举例探索[J].课程教育研究，2018（48）：144-145.

作者简介：马振海（1983.2—），男，回族，籍贯：甘肃广河，本科，中学一级教师，研究方向：高中数学教学。

编辑 冯志强