“直观想象”核心素养的表现形式与培养途径

朱铉

摘 要：人们对“直观想象”这一核心素养的含义理解不到位，存在片面或模糊.其实，直观想象核心素养在中学数学中的主要表现形式为图形直观、空间想象和数形结合，应分别通过模型教学、找“高”训练和数形结合来培养学生的直观想象核心素养.

关键词：直观想象;数形结合;模型教学;核心素养

中学数学的六大核心素养：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析，其实并不是什么新的东西，人们对数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析这五大素养都能正确地理解它的含义，唯独对“直观想象”这一核心素养的含义理解不到位.实际上，《普通高中数学课程标准（2017年版）》给出了直观想象的明确定义：直观想象是指借助几何直观和空间想象感知事物的形态与变化，利用空间形式特别是图形，理解和解决数学问题的素养.其主要包括：借助空间形式认识事物的位置关系、形态变化与运动规律;利用图形描述、分析数学问题;建立形与数的联系，构建数学问题的直观模型，探索解决问题的思路[1].因而直观想象核心素养在中学数学中的主要表现形式为图形直观、空间想象和数形结合，那么我们应当如何培养学生的直观想象能力呢？

一、利用平面几何中的“基本模型”培养学生的几何直观

平面几何是立体几何和解析几何的基础，在平面几何的学习过程中，学生的识图和作图能力得到了培养，而对图形的辨别、拆分与重组能力就是“直观想象”核心素养的表现形式之一.在平面几何的学习中，有许多基本图形以及它们所得到的结论我们称之为“基本模型”，许多看似复杂的图形实际上都由这些基本模型组合而成的，记忆和熟练掌握这些基本模型，并能从复杂图形中辨认它属于哪一类基本模型，或是由哪些基本模型复合而成，这就是直观想象的核心素养水平达成的表现.

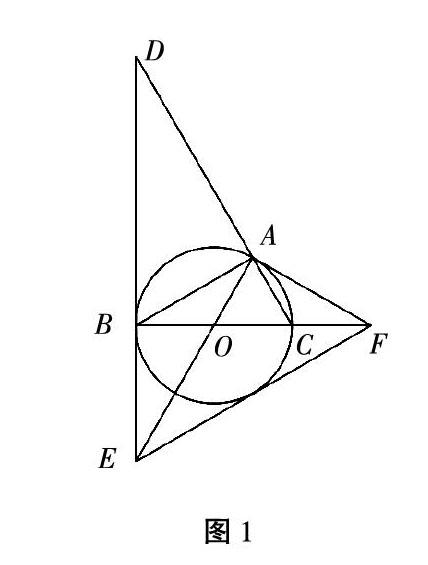
例1 如图1，⊙O是ΔABC的外接圆，BC是⊙O的直径，∠ABC=30°，过点B作⊙O的切线BD，与CA的延长线交于点D，与半径OA的延长线交于点E，过点A作⊙O的切线AF，与直线BC的延长线交于点F.

（1）求证：△ACF∽△DAE;

（2）若S△AOC=，求DE的長;

（3）连接EF，求证：EF是⊙O的切线.

这里着重说明图形的辨别与拆分，所以略去解答过程.本题的图形看似复杂，实际上它是由以下四个基本模型复合而成的：图2的弦切角模型，图3的等腰梯形模型，图4的直角三角形模型以及最常见的等腰三角形模型.这几个基本模型是平时学习和练习过程中常见的，学生对它们可得出什么结论非常了解，只要将复杂图形中的基本模型辨别出来并进行拆分，学生就不难找到解题的思路和方法.而对复杂图形的辨别和拆分能力就是“直观想象”核心素养的一种表现，日常教学过程中引导学生注重基本模型的研究，吃透基本模型，然后强化对复杂图形的辨别和拆分能力的训练，不仅能提高学生的解题能力，还能提升学生“直观想象”的核心素养.

基本模型既包括定义、定理的代表图形，又包括在生活中、练习中经常遇到的图形，还包括由实际问题抽象出来的数学问题.在教学过程中，教师应善于引导学生整理归纳出基本类型和方法，并把类型、方法和范例合为一体形成“基本模型”来记忆和积累.当遇到一个几何问题时，我们能辨认和拆分它们并以此为索引，在记忆贮存中提取出相应的方法来加以解决，这是培养学生“直观想象”核心素养的一种方法.

二、利用找“高”训练培养学生的空间想象

在立体几何中，“高”常扮演“关键先生”，从简单的三视图到复杂的求二面角的平面角，都能见到“高”的身影，然而，我们的“关键先生”往往不容易找到，因此在立体几何教学中，培养学生找“高”能力是培养学生空间想象的重要途径，而空间想象是“直观想象”的另一种表现，培养学生的空间想象能力就是培养学生“直观想象”的核心素养.

例2 某四棱锥的三视图如图5所示，试画出些四棱锥的直观图.若三视图如图6所示呢？

设计意图：给出实物画三视图，给出三视图画直观图是培养学生空间想象非常有效的途径，学生在不断地构建的过程中，空间想象能力逐步培养和增强，而给出三视图画直观图的关键是找到几何体的“高”所在的位置.本例通过改变侧视图和俯视图的形状达到训练学生找”高”能力的目的（作画略）.

例3 在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD为矩形，AP=AB=■BC，Q为BC的中点，求二面角A-PD-Q的余弦值.

本例是求二面角的常见例题，但在教授本例时，我们不应满足于用空间向量来求二面角，而应引导学生在这一基础上，探索采用逻辑法（演绎法）来求二面角，从而使学生的空间想象和逻辑推理能力都得到培养.

采用逻辑法（演绎法）来求二面角的关键是要找到一个平面到另一个平面的垂线，也就是“高”.要想找到这一条“高”我们就要找到面面垂直，利用面面垂直的性质定理来找“高”，面面垂直的性质定理告诉我们，在一个平面内作交线的垂线，必与另一个平面垂直.所以我们只要找到面面垂直，再在一个平面内向另一个平面作交线的垂线即可，通过这种训练，学生逐步构建起线线关系、线面关系和面面关系，并逐渐明晰它们之间的关系，从而构建起自己的空间体系，符合了构建主义的学习和教育观.

三、注重数形结合思想的渗透，培养学生的核心素养

《普通高中数学课程标准（2017年版）》指出：利用图形描述、分析数学问题;建立形与数的联系，构建数学问题的直观模型，探索解决问题的思路.脑科学告诉我们，人类处理图形的能力先于且强于文字能力，所以说数形结合思想是人类将复杂、抽象问题简单化的一种重要思想.实际上，数形结合的思想贯穿于整个中学数学，从初一的数轴到高中的函数，从初中的解方程应用题到高中的解析几何等，数形结合的身影无处不在.

虽然大家都知道数形结合思想的重要性，但很多教师在教学过程中仍然热衷于无图推理，美其名曰培养学生的逻辑推理能力，殊不知数学有六大核心素养，逻辑推理只是其中的1/6，我们应当大力推行数形结合，提出“不作图就不做数学题”的口号.比如说，在解一元二次不等式ax2+bx+c>0（a≠0）的教学中，当Δ>0时，学生在解出一元二次方程ax2+bx+c=0（a≠0）的两根后不会得出不等式的解集，这时教会并要求学生一定要画图，利用数形结合思想来解一元二次不等式，不仅能使学生理解解不等式的原理，还能减少学生的错误.同时，当Δ=0或Δ<0时，不等式ax2+bx+c>0（a≠0）的解集如何取得，是学生的学习难点，利用数形结合思想能轻松突破这一难点.

四、结语

数学家笛卡尔早就说过：“没有图形就没有思考”.美国数学家斯蒂恩斯也说：“如果一个特定的问题可以转化为一个图像，那么就整体地把握了问题，并且能创造性地思索问题的解法”.通过图形，人们能够更直观地理解事物的本质，这就是人们常说的“用图形说话”.所以培养学生的直观想象核心素养就是要让学生学会用图形思考，用图形说话，能从图形中洞察解决问题的线索.我们在教学中应当关注培养学生的图形直观、空间想象和数形结合，并坚定不移地贯彻在整个中学数学教学过程中.

编辑 李建军