一种基于深度学习的环形阵列混合波束成型大规模MIMO系统DOA估计算法

张永皓 苏雪嫣 胡蝶

摘 要：研究了采用混合波束成型结构和环形阵列的大规模多输入多输出系统中的波达方向（direction of arrival，DOA）估计，提出了一种基于深度学习的低复杂度的DOA估计算法。所提算法首先离线训练一个深度神经网络，然后再利用该网络进行在线DOA估计。在线估计中，算法首先将接收信号送入网络，然后根据网络给出的初始角度估计产生一个候选角度集合，最后选择集合中最大似然估计结果最优的角度作为最终DOA估计值。仿真结果显示，与传统的最大似然方法相比，提出的算法可以提供更好的估计性能，且具有更低的计算复杂度。

关键词：大规模MIMO;DOA估计;环形阵列;混合模数波束成型;深度学习

中图分类号：TP 311

文献标志码：A

文章编号：1007-757X（2020）11-0001-04

Abstract：In this paper， the direction of arrival （direction of arrival， DOA） estimation in massive multi-input multiple-output systems with hybrid beamforming structure and uniform circular array is studied， and a low complexity DOA estimation algorithm based on deep learning is proposed. The proposed algorithm is to first train a deep neural network offline， and then use the network for online DOA estimation. In the online estimation， the algorithm first sends the received signal to the network， and then generates a candidate angle set according to the initial angle estimation given by the network. Finally， the optimal angle estimation is selected from the set as the final angle estimation value. The simulation results show that compared with the traditional maximum likelihood method， the proposed algorithm can provide better estimation performance and lower computational complexity.

Key words：massive MIMO;DOA estimation;uniform circular array;hybrid beamforming;deep learning

0 引言

大规模多输入多输出（multiple-input multiple-output， MIMO）是第五代（5G）移动通信系统中的核心技术之一。均匀线性阵列（uniform linear array， ULA）、均匀矩形阵列（uniform rectangular array，URA）、均匀环形阵列（uniform circular array，UCA）是3种常见的MIMO天线配置。与ULA和URA相比，UCA的明显优点在于由于不存在边缘阵元，其方向图可以在阵列平面上进行旋转而不会引起波束形状的显著变化，具有更高的稳定性。因此，本文考虑采用UCA的大规模MIMO系统。

近年来，大规模MIMO系统中的波达方向（direction of arrival，DOA）估计受到了较多的关注。一些传统的基于子空间的方法，如ESPRIT（estimation of signal parameters via rotational invariance technique）、MUSIC（multiple signal classification）、Root-MUSIC等算法被广泛应用于大规模MIMO系统的DOA估计中。文献[1]针对环形阵列接收信号，采用相位模式激励，构造具有正交性的波束子空間，然后再使用MUSIC算法进行DOA估计。针对UCA系统，文献[2-3]等文章也提出了基于子空间的改进的DOA估计算法，其中文献[2]推导了定向环形阵列系统的Cram-Rao界，并定量给出了阵列不同参数对算法性能的影响;文献[3]提出了基于定向天线环形阵列的特征空间算法，与传统子空间算法相比可以降低计算复杂度。文献[4]对导向矢量进行相关运算，寻找到和入射角最接近的天线角度，然后通过在天线角度附近一个很小的范围内进行穷举搜索得到DOA估计。但这些都没有提到环形阵列混合波束成型结构中的相关解决办法。

对于实际的大规模MIMO系统，采用全数字域波束成型（也即采用与天线数相同的射频链路数）的硬件成本和能量消耗将很高。因此，为了兼顾系统性能与硬件成本，所以需要提出新的波束成型估计算法[5]。但由于硬件限制，现有的绝大多数波束成型算法无法照搬到混合波束成型结构下。针对混合波束成型大规模MIMO系统，已有一些文献提出了相应的DOA估计算法[5-7]。文献[5]根据类似的范德蒙结构，提出了改进的Root-MUSIC算法。在文献[6]中，在多个时刻接收信号，然后对信号进行组合，形成与普通大规模MIMO系统相同的接收信号，再用MUSIC算法进行DOA估计。文献[7]和文献[6]思想类似，先对信号进行多次接收、组合，然后通过DFT变换对组合信号的噪声分量进行白化，将接收到的信号转化为与普通MIMO系统相同的信号，对相干信号效果很明显。然而，文献[5-7]都只考虑了ULA，所提出的算法并不适用于UCA。

到目前为止，针对环形阵列混合波束成型大规模MIMO系统的DOA估计问题还没有得到很好地解决。尽管传统的最大似然（maximum likelihood， ML）方法可以用来估计DOA，但ML方法的计算量巨大，在实际中的应用受到了诸多限制。近年来，深度学习技术发展迅猛，其中，在目前应用较广的深度学习网络——深度神经网络（deep neural network， DNN）在信号处理领域展现了非凡的潜质，它能够利用大数据降低实际系统实现中的复杂度，提升系统性能，被广泛应用于分类、回归等问题。有研究表明，深度学习已经开始用在信道估计、信道检测、CSI反馈与重建等无线传输技术当中[8]。其中文献[9]提出利用DNN建立入射角到接收信号的映射，从而实现ULA混合波束成型大规模MIMO系统的DOA估计。

本文将针对上述问题，提出一种低复杂度的DOA估计算法。在本文中，我们将环形阵列混合波束成型大规模MIMO系统的DOA估计建模为信号回归问题，并引入深度学习技术来解决这一问题。具体实现过程如下，首先离线训练一个深度神经网络（deep neural network， DNN），然后利用训练好的网络进行DOA在线估计。在线估计中，将接收到的信号向量送入网络，由网络给出角度的初始估计。本文算法基于该估计值产生一个角度候选集合，选择其中最大似然估计最准确的角度作为最终的DOA估计值。仿真结果表明，与传统最大似然算法相比，本文算法能以更低的计算复杂度提供更好的估计性能。

本文内容安排如下：第1节介绍系统模型，第2节介绍传统最大似然估计算法，第3节提出了基于深度学习的低复杂度的DOA估计算法，第4节为仿真结果和相关结论，第5节为本文小结。

1 系统模型

考虑一个采用UCA和混合波束成型结构的大规模MIMO系统，如图1所示。

式中，s（l）为第l时刻训练符号。这里为了描述方便省略时刻索引值l。

由于目标函数是φ的非线性函数，因此需要采用一维搜索来求解式（5）。具体搜索空间如式（8）。

采用穷举搜索可以得到式（7）的解。可以看到，在这种情况下，算法的计算复杂度将为O（GNN2RF），其中G表示集合G的元素个数。因此，当搜索步长小、天线数较多时，最大似然估计算法的计算复杂度将非常高。

为了获得实际可行的DOA估计算法，第4节将基于此提出一种低复杂度的估计算法。

3 基于深度学习的低复杂度DOA估计算法

在本节中，DOA估计问题将被建模为一个信号回归问题，然后通过神经网络来求解这一问题。

根据式（1）可以看到，接收向量

3.1 离线训练

算法所用的DNN基本结构，如图2所示。

网络训练时要用损失函数。损失函数是用于学习的反馈信号，用来衡量预测值和真实值的误差，神经网络的训练过程就是让损失函数最小化的网络优化过程。对回归问题，常用的损失函数是均方误差MSE （mean-squared error）：

因此本文算法中也采用该损失函数。

DNN网络的各种参数通过训练确定。训练过程分为以下两个步骤。

3.2 在線估计

当网络训练好后即可将其用于DOA估计。具体的，当接收到向量y后，首先取其实部和虚部得到向量r，然后将其送入网络，网络的输出即为φ0的估计。然而，由于实际中噪声的影响，当信噪比较低时，网络的输出和真实值还会存在一定偏差。因此，为了提高估计性能，我们将神经网络的输出作为角度估计的初始值，然后再利用最大似然的思想，在初始值附近的一个小范围内进行穷举搜索，得到最终的角度估计，如表1所示。

4 仿真结果

考虑一个天线数为N = 128，射频链路数为NRF=32的环形阵列大规模MIMO系统。本文采用归一化均方误差（NMSE）作为DOA估计的性能指标。仿真首先比较了系统在不同天线配置、不同射频链路连接方式下的DOA估计性能，共包含如下四种配置：全向天线全连接、全向天线部分连接、定向天线全连接和定向天线部分连接。全连接时，

VA如式（5）所示;部分连接时，

VA如式（6）所示。采用全向天线时，gn（φ0）=1;采用定向天线时，gnφ0可由式（3）计算得到，其中取m=50。

四种配置下传统最大仍然DOA估计算法性能，如图3所示。

图3给出了系统在4种配置下，采用传统ML方法估计DOA的NMSE性能，其中搜索步长Δφ=0.25π/180 （即为0.25）。从图中可以看到，采用全向天线全连接配置可以获得最好的估计性能。

四种配置下基于深度学习DOA估计算法的性能比较，如图4所示。

图4给出了在四种配置下，基于深度学习方法估计DOA的NMSE性能。仿真中的神经网络包含1个输入层、4个隐层和1个输出层，各层均为全连接层。其中，输入层包含256个节点，激活函数为ReLU;4个隐层的节点个数分别为256、128、64、32，激活函数为ReLU;输出层包含一个节点，无激活函数。在离线训练时，产生100万个训练数据，训练轮次设为20;在线估计中，我们取e=5π/180（也即5°）。从图中可以看到，采用全向天线部分连接配置可以在中低SNR情况下获得最佳估计性能，而采用全向天线全连接配置，可以在较高SNR情况下获得最佳估计性能。

全向天线链接下本文算法与ML算法的性能比较，如图5所示。

图5给出了系统在全向天线全向连接的配置下，本文算法与传统ML方法的NMSE性能比较，其中本文算法的搜索区间分别取e=0（也即0°），e=5π/180（也即5°）和e=10π/180（也即10°）。从图中可以看到，随着信噪比的增大，本文算法可以提供比传统ML算法更好的估计性能。

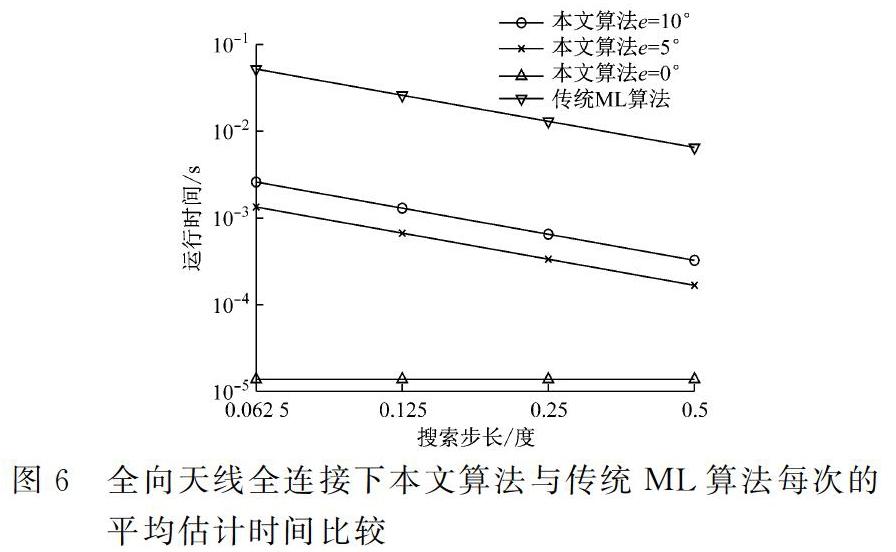
全向天线全连接下本文算法与传统ML算法每次的平均估计时间比较，如图6所示。

图6给出了系统在全向天线全向连接配置下，本文算法与传统ML算法在不同搜索步长下运行时间的比较，其中SNR=30 dB，本文算法的搜索区间分别取e=0，e=5π/180和e=10π/180。从图中可以看到，本文算法的运行时间比传统ML算法减少了至少一个数量级，即与传统ML算法相比，本文算法可以极大地降低计算复杂度。

图5和图6的仿真结果表明，与传统ML算法相比，本文算法可以在提供更佳估计性能的同时，极大降低系统的计算复杂度，适合实际实现。

5 总结

本文研究了采用均匀环阵和混合波束成型结构大规模MIMO系统的DOA估计问题，提出一种基于深度学习的低复杂度DOA估计算法。其核心思想是将DOA估计建模为一个信号回归问题，再离线训练DNN网络来解决。然后，离线训练好的网络将用于在线DOA估计。在线估计中，我们首先将接收到的信号向量送入网络，得到角度的初始估计，然后基于初始估计产生角度候选集合，最后再利用ML方法，在所有候选角度中选择最终估计值。仿真结果表明，与传统ML算法相比，本文算法能提供更好的估计性能，且计算复杂度更低。

参考文献

[1] Mathews C， Zoltowski M. Eignestructure Techniques for 2-D angle estimation with uniform circular arrays[J]. IEEE Transactions on Signal Processing， 1994， 42（9）：2395-2407.

[2] Jackson B， Rajan S， Liao Bruce， et al. Direction of arrival estimation using directive antennas in uniform circular arrays[J]. IEEE Transactions on Antennas and Propagation， 2015， 63（2）：736-747.

[3] Pesavento M， Bohme J. Direction of arrival estimation in uniform circular arrays composed of directional elements[C].Sensor Array and Multichannel Signal Processing Workshop Proceedings， Rosslyn， 2002：503-507.

[4] Li Q，Su T， Wu K. Accurate DOA estimation for large-scale uniform circular array using a single snapshot [J]. IEEE Communications Letters， 2019， 23（2）：302-305.

[5] Shu F， Qin Y， Liu T， et al. Low-Complexity and high-resolution DOA estimation for hybrid analog and digital massive MIMO receive array[J]. IEEE Transactions on Communications， 2018， 66（6）：2487-2501.

[6] Chuang S， Wu W， Liu Y. High-Resolution AOA estimation for hybrid antenna arrays[J]. IEEE Transactions on Antennas and Propagation， 2015， 63（7）：2955-2968.

[7] Trigka M， Mavrokefalidis C， Beridis K. An effective preprocessing scheme for DOA estimation in hybrid antenna arrays[C]. 2018 June 25th International Conference on Telecommunications （ICT）， St. Malo， 2018：127-131.

[8] 張静， 金石， 温朝凯， 等，基于人工智能的无线传输技术最新研究进展[J]. 电信科学， 2018， 34（8）：46-55.

[9] Huang H， Yang J， Huang H， et al. Deep Learning for Super-Resolution Channel Estimation and DOA Estimation Based Massive MIMO System[J]. IEEE Transactions on Vehicular Technology， 2018， 67（9）：8549-8560.

（收稿日期：2019.10.23）