政府与港口在排污治理中的演化博弈分析

孟凡锋 都晓惠

摘 要：航运业的快速发展给港口周围环境带来了巨大的压力。如何正确处理好环境保护和经济发展两者的关系，成为政府和港口双方重点关注的问题。基于前者提出的复制动态方程，建立政府和港口之间的博弈矩阵，分析两者在演化过程中策略选择的演化过程并借助了相关软件进行了仿真模拟分析。研究表明， 双方在该过程中所投入的成本以及获得的收益是影响两者演化博弈趋势的主要因素，同时受双方初始状态及利益最大化影响。最后从政府补贴、港口排污治理积极性、公众参与等方面提出了建议。

关键词：环境污染;演化博弈;数值仿真

中图分类号：X5             文献标识码：A            文章编号：1006—7973（2020）11-0128-03

1 引言

港口的水污染、大气污染和噪声污染对水生生物产生影响的同时，也对操作人员和周围居民带来严重的危害。在使用演化博弈模型研究政府环境规章制度与港口排污策略行为问题时，政府与港口不能满足完全理性的假设，双方在长期博弈的过程中根据对方策略的变化而调整，这种情况与生物进化博弈过程中的“复制动态”机制具有非常高的契合度[1]。因此，本文基于演化博弈模拟分析双方选择和调整策略的过程。

演化博弈论源于生物进化理论的有限理性行为假设，该理论认为参与博弈的群体在演化过程中根据对方策略的调整而调整，最终达到稳定均衡的状态 [2]，该策略提出以后，受到学者的普遍关注并被应用到相关领域。杨扬[3]等运用演化博弈研究了国际和国内港口协同合作的演化过程，通过数值分析仿真模拟分析了各阶段演化趋势和轨迹。赖成寿[4]在参与方理性的条件下，运用该理论研究不同港口的竞争行为的演化规律。刘家国[5-6]等将运输企业和政府监管部门作为参与博弈的主体，分析了不同安全事故发生率下的演化稳定策略;韩震[7]等建立了基于系统动力学的演化博弈模型，研究了不同参数值的变化对港口安全问题的影响。在港口资源方面，舒昶[8]等基于博弈论的视角，建立当代人和后代人之间的博弈模型，对海岸线资源进行了合理的配置。综上所述，大多文献将演化博弈应用于港口的发展，资源的配置等研究较多，但对于港口环境保护，污染物的治理虽然有了相关意识，但对此分析的文章较少。本文基于由Taylor和Jonker[11]提出的复制动态方程，建立政府和港口之间的博弈矩阵，分析两者在演化过程中策略选择的演化过程，借助Matlab软件模拟出不同策略下的演变情况，并根据结果给出相关建议。

2 演化博弈模型

本文假设如下：

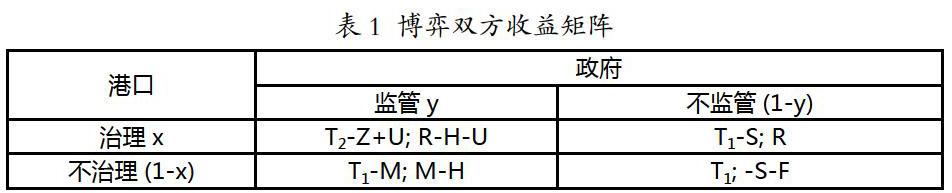
假设1：如果港口选择对污染物进行治理将投入一定的资金，设整改所投入的资金为Z;进行整改后带来的积极收益为R;港口选择治理排污措施前的收益为T1，港口选择治理排污措施后的收益为T2。

假设2 ：设政府进行监管成本为H，港口对于污染选择不治理而带来的罚金为M。政府对积极治理污染物的港口进行补贴，补贴数额为U;若政府监管且港口对污染物不进行治理对环境所产生的影响经济损失为S，人民公信度损失为F。

港口选择治理污染物的数量增长率    为：

f1 - f12 =（1- x）[y （T2 - Z + U - T1 + S + M）-S]                                 （1）

政府选择监管策略的期望收益率为：

f3 = （R - H - U） x+（M - H）（1- x）

政府选择不监管策略的期望收益率为：

f4 = Rx + （-S - F）（1- x）

平均期望收益率为：f34 = yf3 +（1- y）f4

同理，政府選择监管策略的数量增长率：

= f3 - f34 = （1- y） [x （-U - M - S - F） +M - H +S+F]                              （2）

将（1）（2）联立得到双方的复制动态方程：

对该复制动态方程求偏导得出该系统的雅克比矩阵J：

矩阵的行列式为：

（1-2x） [y（T 2 - Z + U - T 1 + S + M） -S] （1-2y） [x （-U - M - S - F） +M - H + S + F] - x（1 - x）（ T 2 - Z + U - T 1 + M） y （1- y）（ -U - M - S - F）

矩阵的迹为：

Tr J = （1-2x） [y（T 2 - Z + U - T1 + S + M） - S] （1 - 2y） [x （-U - M - S - F） + M - H + S + F]

在联立的复制动力方程中令   =0，  =0，可以得到演化稳定均衡点：O（0，0）， A（1，0），B（1，1）， C（1，1）， D （x， y），其中

判定系统达到稳定状态的两个条件为雅克比矩阵行列式Det J > 0且迹Tr J < 0。此时该点为系统的ESS（演化稳定策略）。根据以上判定条件可得出该系统的演化稳定均衡点，如表2所示。

3 演化仿真分析

为了更加清楚了解政府和港口两者在演化博弈中的具体关系，本文运用Matlab对两者之间的动态演化过程进行了仿真模拟分析。

图1是T2 - T1 < Z， R - S - F < H条件下的模拟情况。表示的现实含义是当港口选择治理污染物后所增加的收益T2 - T1较少，甚至低于整改投入的资金Z时，在这种情况下港口迫于政府的压力选择进行整改。但由于港口的利润一直处于减少的状态，在一段时间后，港口会选择放弃进行污染物治理，同时政府选择监管所获得的社会效益与不监管所造成的经济损失S，公信度损失F之差小于其整改所投入的资金，最终，系统将会演化成x=0，y=0的稳定状态，在满足上述的条件下，假设不同的数值进行模拟。则政府与港口的动态演化趋势如图1所示。图1（a）表示随着系统的演化，政府选择不监管的概率逐渐趋近于0;随后如图1（b）所示港口选择治理污染物的概率受到政府监管概率的减小而逐渐趋近于0;最终如图1（c）所示两者最后都会演化到稳定点（0，0），在这种状态下，港口和政府都选择了“消极”的态度，与国家倡导的环境友好型社会背道而驰。

图2是T2 - T1 < Z，R - S - F > H，T2 - T1 + U < M条件下的模拟情况，该图表示的现实含义是当港口选择治理排污的收益T2 - T1小于投入的资金Z时，但满足R - S - F > H即政府选择监管的收益大于成本，政府对港口排污进行监管以响应国家的政策。形成不稳定均衡系统，最终该均衡系统会演变成（0，1）的状态。在满足上述的条件下，假设不同的数值进行模拟。则政府与港口的动态演化趋势如图2所示，在这种状态下不利于港口城市发展和环境保护，同时对政府的管理也带来了不便。

图3是T2 - T1 + U - M > Z， H + U < R - S - F + M条件下的模拟分析。港口采取排污治理后的收益与政府的各项补贴之和大于其投入成本且政府进行监管后相关群体所带来的社会收益和对拒不对排污进行治理的港口所处的罚金与不监管所产生的经济损失与公信度损失之差仍大于其进行监管时的总投入，在这种情况下政府会倾向于进行监管来提供支持，如图3（a）所示，最终该系统会发展成为（1，1）的稳定状态，如图3（c）所示，即政府选择监管，港口进行排污治理。这种情况下对环境的改善起到了很大的作用。

最后一种情况是T2 - T1 > Z， H + U > R - S - F + M，这种情况下属于港口自发的进行整改，但在当前的环境下，整改的成本过高以及政策的不支持等因素，这种稳定的系统状态很难实现。故不做讨论。

4 结语

本文构建了政府和港口两者之间的演化博弈模型，并进行了模拟数值仿真。研究结果表明：影响演化行为关键因素为双方在该过程中所投入的成本以及获得的收益;同时受博弈双方初始状态及利益最大化影响，双方很难通过自发的良性循环达到一种稳定平衡状态。基于以上研究结论，提出相关建议如下：

第一，国家对积极参与环境保护的主体在税收方面进行减免，提高港口治理污染物的积极性。

第二，港口在治理排污的过程中积极寻找合作伙伴，降低成本。采取绿色生产的模式，提高社会声誉。

第三，通过信息共享代替政府部分的监督职权，降低政府监管成本，提高政府的公信度。

参考文献：

[1] 侯贵生，殷孟亚，杨磊.政府环境规制强度与企业环境行为的演化博弈研究[J].统计与决策， 2016， 000（021）：174-177.

[2] Chesbrough H， Prencipe A. Networks of innovation and modularity： a dynamic perspective[J]. International Journal of Technology Management， 2008， 42（4）：414-425

[3] 楊扬，袁媛.基于演化博弈的国际陆港与海港协同演化研究[J].昆明理工大学学报（社会科学版），2017，17（05）：73-80.

[4] 赖成寿，吕靖，李慧等.基于演化博弈的港口竞合策略选择及仿真研究[J].重庆交通大学学报（自然科学版），2018，37（11）：112-118.

[5] 刘家国，王军进，周欢等.基于安全风险等级的港口危化品监管问题研究[J].系统工程理论与实践，2018，38（05）：1141-1152.

[6] 刘家国，周欢，王军进等.演化博弈视角下的港口危化品监管机制研究[J].哈尔滨工程大学学报，2019，40（03）：628-633.

[7] 韩震，王菡，孟好.基于系统动力学的港口危险品管理演化博弈分析[J].大连海事大学学报，2019，45（02）：28-35.

[8] 舒昶，张林波.基于博弈视角的港口岸线资源代际配置分析[J].生态经济，2015，31（06）：118-121.

[9] Taylor P D， Jonker L B. Evolutionary Stable Strategies and Game Dynamics[J]. Mathematical Biosciences， 1978， 40（1-2）：145-156.