频域空间密度矩阵重正化群的研究进展

2020-12-23任佳骏帅志刚

高等学校化学学报 2020年12期

姜童，任佳骏，帅志刚

（清华大学化学系,教育部有机光电子与分子工程重点实验室,北京100084）

在量子多体问题中，波函数的精确求解受到“指数墙”的制约，因此在有限的计算资源下对波函数进行合理的近似是一种常用手段.1992年，White［1，2］提出了密度矩阵重正化群（Density matrix renormalization group，DMRG）理论.DMRG利用约化密度矩阵的本征矢量在实空间的局域性来降低希尔伯特空间的维数，通过反复迭代变分优化系数，成为了一种求解多体波函数的有效方法.该方法成功地应用于求解一维强关联格点模型中的低能电子态的电子结构，如对于短程作用的Hubbard模型、Heisenberg模型等给出了接近精确解的结果.Shuai等［3～8］很快地将DMRG推广到具有长程相互作用的半经验量子化学中，并用以研究共轭高分子的低能级激发态次序以及线性、非线性光学响应等问题，这被国际学术界视为DMRG在量子化学领域应用的开端.White等［9］和Chan等［10］发展了从头算的DMRG算法，并成功应用于过渡金属中心配合物以及大有机共轭体系的电子结构计算中.DMRG的含时理论和响应理论（Time dependent DMRG，TD-DMRG）［11～16］以及频率空间算法［5，8，17～27］的快速发展使得DMRG能够用于动态响应性质的计算.TD-DMRG通过含时演化得到时间关联函数，而后通过傅里叶变换得到频域信息，该方法在包括线性光谱计算［15］、激子分离［28］、分子的超快内转换［29，30］以及单态裂分［31，32］等有机半导体体系的光物理过程得到了广泛应用.然而在含时演化过程中体系的纠缠会随着时间快速增长［33～35］，在有限的变分空间中演化的误差增大，从而对长时间演化带来了挑战，另一方面，傅里叶变换得到的谱图的精度取决于演化时间的长度.

频率空间的算法为动态响应函数的计算提供了不同角度.1995年，Hallberg［17］首次将基于Lanczos递归的连分数展开（Continue fraction expansion，CFE）方法与DMRG结合，并应用于频域自旋关联函数的求解.这种方法简单易行，但精度较低，只适用于计算低能态的较为简单的分立谱［20］.随后，Ramasesha和Shuai等［5，8］提出了更精确的修正矢量密度矩阵重正化群CV-DMRG（Correction vector DMRG）方法，可以精确地计算复杂的连续谱函数，并适用于非线性光学响应函数，但需要的计算量更大.基于CV-DMRG的工作方程，Jeckelmann［21］提出一种变分优化的动态DMRG算法（Dynamical DMRG），可以将计算精度提高.该方法更为简洁有效，被视为最精确的计算谱函数的DMRG算法［14，25］.最近，Schollwöck和Delft等［23］将矩阵乘积态（MPS）与Chebyshev多项式展开相结合提出了CheMPS算法，该方法在自旋模型［23］及杂质模型［36］的谱函数计算中实现了计算量与精度之间较好的平衡，但其潜力仍有待进一步探索.Chan等［25～27］和Haegeman等［37］基于含时微扰理论和DMRG波函数的切空间，提出了解析线性响应DMRG方法，也被用来求解线性响应性质.本文将介绍这些频率域发展的动态DMRG响应理论，并重点介绍我们课题组在有限温度发展的算法.

1 密度矩阵重正化群与矩阵乘积态

对于含有N个轨道的系统（i=1，…N），|σi〉代表第i个轨道的d维的正交基组（如对于电子系统，每个空间轨道存在|↑〉，|↓〉，|↑↓〉，|vacuum〉4种电子占据状态，d=4；而对于玻色子系统，d原则上是无限大，因此需要做截断），整个系统的希尔伯特空间|σ1…σN〉=|σ1〉⊗…⊗|σN〉为dN维，精确解可以用完全组态相互作用（Full configuration interaction，FCI）的波函数表示：

式中，系数cσ1…σN共有dN种取值，因此对于稍大的体系便难以实现精确对角化.DMRG波函数采用可变分优化的MPS作为波函数的拟设，即将高维向量cσ1…σN分解为N个低秩矩阵乘积的形式［38，39］：

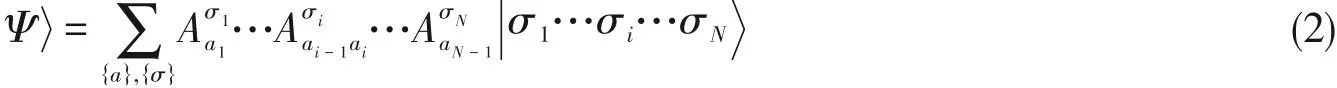
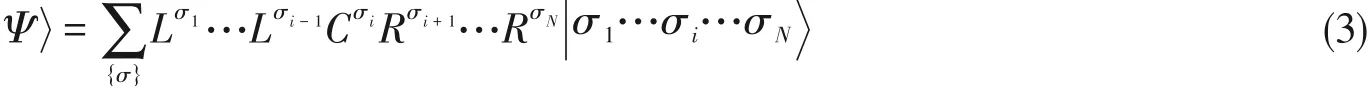
式中，Lσ与Rσ分别是左规整与右规整的矩阵，即［见图1（D）和（E）］为重正化基|lai-1〉|σi〉|rai〉下的系数矩阵：

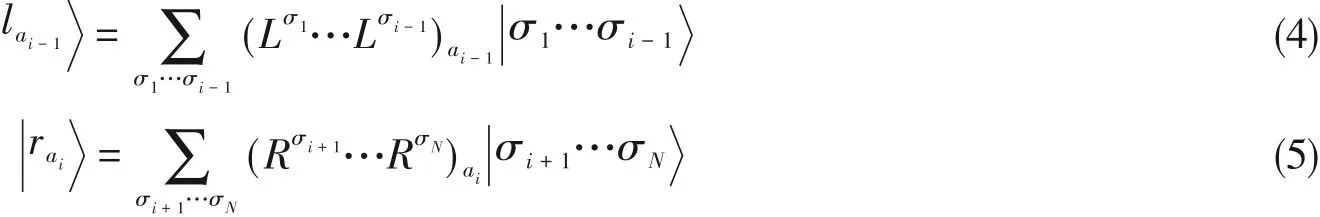
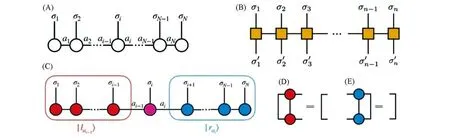
Fig.1 Graphical representation of matrix product state/operator(MPS/MPO)of wavefunction and operator

传统的DMRG并不显式地构造全空间下的算符，而是处理算符在重正化基下的投影，如第i个格点的哈密顿量的投影其中在MPS出现后，对于任意的算符也可以被自然地表示为矩阵乘积算符（Matrix product operator，MPO）的形式（如下式），见图1（B），MPO的局域矩阵是一个四维张量，wi-1与wi被称为“虚拟键”被称为“物理键”.这使得DMRG在形式上变得更为简洁，同时也提高了某些算法的精度.

Fig.2 Adding two different MPOs

当一个局域矩阵维数为D的MPO作用到虚拟键维数为M的MPS上后，会得到一个维数为MD的新MPS，如图3所示，在很多场景中，新得到的MPS的维数较高，因此需要通过奇异值分解（SVD）分解或者变分的方式做压缩.

Fig.3 Applying an MPO to an MPS

Fig.4 Overlaps and expectation values

DMRG通过扫描的方式对波函数进行迭代优化，以单格点的DMRG算法为例，当优化到第i个格点，对式（3）中的Cσi变分来最小化拉格朗日函数为变分系数，其收敛的结果对应于的本征能量，而后得到式（7），利用的左右规整性，可将该方程进一步简化为一个特征值问题，见图5.

Fig.5 Eigenvalue problem when minimizing the Lagrangian with respect to local matrix Cσi

2 线性响应理论

下面将简要介绍线性响应理论，并推导频率空间的响应函数在有限温度及零温度下的函数形式.未加说明的，物理量均用原子单位.

对于处于热平衡（温度为T）的正则系综，其密度矩阵表示为其中配分函数Z(β)=为玻尔兹曼常数当系统受到来自外界势场的f(t)V的扰动时，其哈密顿量表示为

式中，f(t)为外势场的强度；V^为系统的可观测物理量，满足V^=V^†；当系统受到的扰动比较小时，利用线性响应理论，O^(t)的热力学期望值用Kubo方程［40］表示为

式中，χ(t-t′)被称为推迟格林函数（仅当t＞t′时，不为0），

式中，θ(t-t′)为单位阶跃函数；O^(τ)=eiH^0τO^e-iH^0τ；[·，·]为对易关系（即是指关于的密度矩阵求期望.将χ(t-t′)做傅里叶变换到频率空间可得：

式中，Em，En分别对应于的第m和第n个本征态的本征能量.

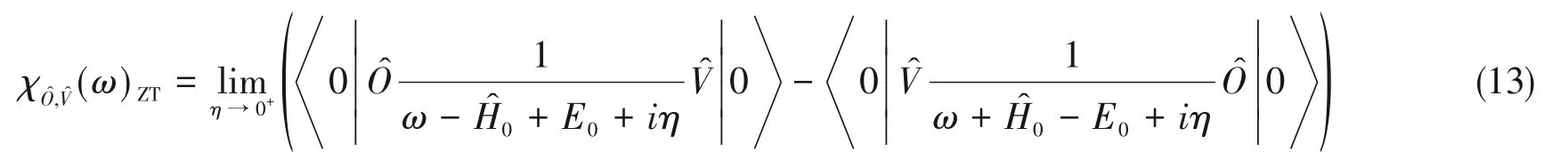
式中，

0 为基态波函数.

其正比于体系吸收外界势场能量的速率.

3 零温度下的算法

3.1 Lanczos DMRG

Lanczos迭代算法在数学上被用来求解大型稀疏厄米矩阵的线性方程与特征值问题，其思想是将原矩阵投影到Lanczos递归产生的向量所张成的Krylov子空间上，从而大大降低对角化的难度.该方法最早被Gagliano与Balseiro［42］用来求解零温度下的基态与线性响应，Hallberg［17］将其与DMRG相结合来计算T=0的单粒子响应函数（下式），使其能够处理更大的系统［18，19，43～46］.

式中，第二个等号后为莱曼表示的谱函数.Lanczos DMRG将难以直接处理的哈密顿量投影到Krylov子空间的三对角矩阵Heff：

直接对角化得到子空间中的特征向量与特征值，代入式（15）即可.Heff由Lanczos迭代算法得到，

除了直接对角化Heff，通过连分数展开也可直接得到Lorentz展宽为η的光滑谱图：

式中，z=E0+ω+iη.

Lanczos算法可以在DMRG基态程序基础上较为容易地实现，同时计算量小，在MPS/MPO的框架下，Lanczos算法只需进行将MPO作用到以及MPS之间的求和操作即可快速实现［19］，其实现的细节请参见第1节.但Lanczos只能应用于计算低能态的较为简单的分立谱［20］，这是由于在迭代过程中存在误差累积，同时由于第n+1个Lanczos向量仅依赖于第n个和第n-1个向量，因此与之前n-2个向量之间的正交性逐渐被破坏，Kühner和White［20］提出作为判据及时终止迭代.Dargel等［19］提出了将Lanczos向量重新做正交化的方法，以改善该问题.

3.2 Correction Vector DMRG

早在DMRG被提出之前，Soos与Ramasesha［47］就提出了在精确对角化框架下的修正矢量（Correction vector，CV）方法，求解π电子共轭体系的Pariser-Parr-Pople（PPP）模型的线性与非线性响应光学性质.该方法尽管精确，但限于较小的体系（N＜12）.之后，Ramasesha等［5，8］将DMRG与CV相结合，能够处理更大的体系.为求解式（15），将频率为ω时的CV定义如下：

式（22）可通过扫描的方式在局部的重正化基上利用共轭梯度法进行求解，当采用的展宽η较小时，线性方程在达到共振的位置是接近奇异的，为了提高收敛速度，可以采用预处理条件来减小矩阵的病态程度.在重正化基表示中，第i个格点的投影哈密顿量为需要说明的是，式（22）中的引入增大了条件数（约为原条件数的平方），增加了系统的病态程度，给求解带来困难.此外，传统的DMRG算法不能直接给出需要通过对其进行近似，二者在M→+∞时严格相等，但是在有限的M时会引入额外的误差.

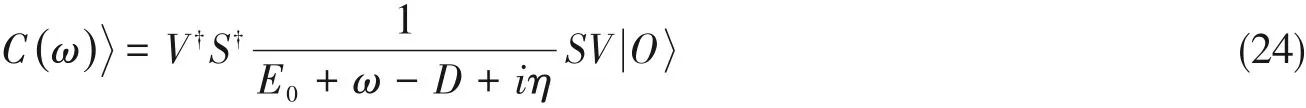
这种方法避免了直接求解式（22），与原始Lanczos DMRG不同的是，这里的密度矩阵考虑了的贡献，即对于不同的ω采用了不同的重正化基去计算，因此更为准确.

3.3 Dynamical DMRG

Jeckelmann［21］基于CV-DMRG进一步提出了变分优化的方法，称为动态DMRG（Dynamical DMRG，DDMRG），将求解CV-DMRG的线性方程［式（22）］转化为最小化的问题：

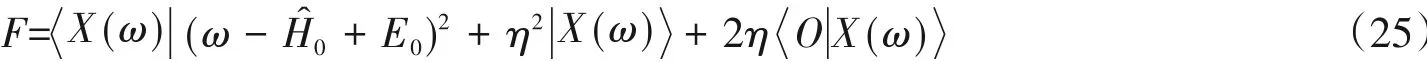
当F处于极小点时，对于谱函数S(ω)［见式（21）］，有因此不必显式地利用求解S(ω)，只要求得F的最小值即可.在此框架下，对于给定的若其误差为O(ε)，则S(ω)的计算误差变为O(ε2)，这便是最小化泛函方法的优势所在.在扫描优化F的过程中，对第i个格点矩阵Aσi进行变分，其余格点保持固定，此时的工作方程为

DDMRG的另一项优势在于其可以自然地推广到MPS/MPO的框架下，式（26）在MPS/MPO框架下的表示如图6（A）所示.这一线性方程可以通过标准的迭代算法，如共轭梯度法进行求解.图6（B）表示将求解后的解进行奇异值分解后，更新局域矩阵，并为下一个位点提供初猜.在传统的DDMRG算法中与基态波函数通过态平均共用一套重正化基［21］，通过将用2个不同的MPS分别表示，将每个态都表示得更加准确，从而提高了计算精度.另一方面，在以往的算法中，局部的表示在重正化基上（见3.2节），因此需要对于包括在内的高阶矩进行近似，而利用MPO表示则可以对此类高阶矩进行精确表示.

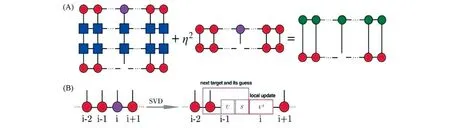
Fig.6 Graphical representation of minimizing the Lagrangian with respect to local matrix Aσi[22]

3.4 Chebyshev多项式展开矩阵乘积态

类似于Lanczos方法，Chebyshev多项式展开的方法利用递归产生一系列的Chebyshev向量来展开响应函数，并被成功应用到Heisenberg模型、Holstein模型、Anderson模型等在零温度或有限温度下的光吸收谱、光电导率等响应性质的计算［49～52］.Schollwöck和Delft等［23］提出了将Chebyshev多项式展开与MPS结合的CheMPS方法.Chebyshev展开的核心思想是采用核多项式展开去近似线性响应函数中的δ函数：

首先，介绍一下其数学背景［52］，对于一般的函数f(x)，可以通过Chebyshev多项式进行展开：

其中，Tn(x)服从三项递推关系：

上述展开仅在x∈[-1，1]成立.因此，为了处理首先做投影与在实际操作中，为了避免数值不稳定带来的问题，要求ω′∈[-W′，W′]，其中W′略小于1：

式中，gn是阻尼系数，这是由于在实际操作中多项式不能展开到无穷阶，因此会产生所谓的吉布斯振荡［23］，引入gn可以达到平滑光谱的效果，如最常用的Jackson系数与Lorentz系数可分别在频率空间达

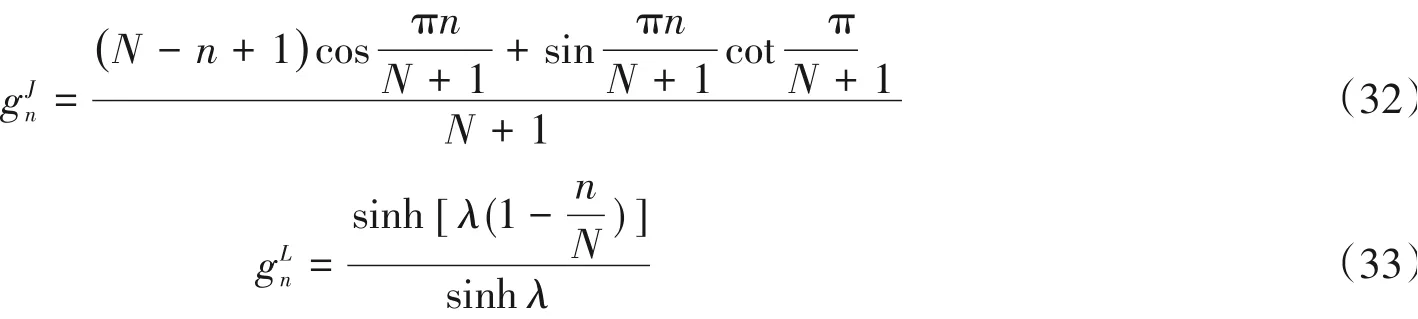
将式（31）代入式（27）可得：

由于系统的整个能量区间W可能很大，此时为了得到较高精细程度的光谱需要演化很多的步数，而实际计算上，存在响应的频率区间相对于系统的整个能量空间会较小，因此可选择将一个有效的能量区间W*投影到[-1，1]之间.当W*＜W时，在每次演化得到对其进行压缩的过程中会引入“高能态”（对应于的特征值大于1的分量），这将导致接下来的演化发散，在此情况下，就很有必要进行额外的能量截断过程［23］，需要通过能量截断将每次引入的“高能态”扔掉.由于的希尔伯特空间难以直接处理，因此需要在局域的格点进行操作，在第i个格点对应的重正化基下的下构造维度为dk的Krylov子空间，将在子空间下的矩阵做对角化可以选取出能量的绝对值大于1的分量构造投影算符而后作用到的第i个格点，移动到下一个点，扫描ns圈后结束能量截断.需要注意的是，并没有严格的方法可以将高能部分全部扔掉，ns与dk的最优组合也并不直接可以得到，ns与dk需要经验地进行选择.

3.5 解析的线性响应DMRG

上述算法可归为一类，首先，这几种方法都直接面向求解线性响应函数［见式（15）］，其次，在与DMRG结合之前，Lanczos方法、CV方法以及Chebyshev多项式展开方法便被独立地用来直接求解线性响应函数.与上述方法不同，解析的线性响应DMRG方法基于DMRG的矩阵乘积态结构，通过微扰理论直接计算波函数的局域格点矩阵对于外界势场微扰的响应［25～27，37］.

对于第1节中关于系统波函数的混合规整表示，将基态波函数表示为

式中，上角标(0)代表系统未经外界势场扰动.当系统受到外界光场V(t)=Veiωt+V*e-iωt的微扰，使得各格点矩阵产生响应：

接下来，移动到第i+1个格点求解当得到收敛的一阶线性响应波函数后，可以求解线性极化率（ω＞0）：

G(ω)对应于式（13）中的第一项，其中μ(0)i是偶极算符在第i个格点对应的重正化基下的投影，C(1)(ω)是关于频率为ω的光场扰动的一阶响应波函数.

4 有限温度下的算法

4.1 有限温度密度算符的求解

DMRG本身是针对波函数的理论，对于有限温度或混合态的情况下则需要用密度矩阵（算符）描述，在热场动力学算法（Thermal field dynamics，TFD）中［53］，处于温度T(T＞0)的任意量子态可以表示在由物理空间P与辅助空间Q构成的扩大的希尔伯特空间P⊗Q中（此辅助空间Q是物理空间P的一个拷贝）.

Fig.7 Graphical representation of obtaining the ensemble expectation value of operator(marked in blue)by thermal field dynamics

因此，ρβ可以表示为在DMRG的框架下，热场动力学也被称为纯化的方法［38，54～56］，借助于MPS/MPO的语言，可以对这一过程进行更为直观的理解，由式（44），可以在虚时间轴从τ=0演化到τ=β/2得到：

由于式（46）不是幺正的，在每演化一步后，ρ(τ)通过进行归一化.

4.2 Lanczos DMRG

Prelovšek［57］等从另一个角度通过对初态进行采样的方式来近似得到热平衡密度矩阵，从而将Lanczos DMRG扩展到了有限温度.T＞0时的密度矩阵表示为

式中，R为取样的数目.对做Lanczos迭代得到三对角的Heff，对角化得到一组特征向量以及特征值从而将作用于上近似为

对于有限温度下的自相关函数χ(1)(ω)［见式（12）］：

4.3 Dynamical DMRG

最近，Shuai等［22］在MPS的框架下，通过纯化密度矩阵的方法建立了有限温度下的DDMRG.对于有限温度下的响应函数S(ω)（参照第2节）：

基于此构造泛函F：

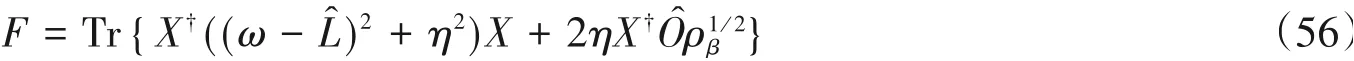
当X(ω)满足式（55）时，F取得全局最小值，同时满足S(ω)=-Fmin/πη.X(ω)可以通过迭代求解方程（下式）进行变分优化［38］（如图8所示）：

4.4 Chebyshev展开矩阵乘积态

在3.4节介绍了零温度下采用Chebyshev展开的DMRG方法.Tiegel等［24］将其推广到求解有限温度的谱函数：

如同零温度的做法，需要先将ω与L投影，对于ω∈[ωmin，ωmax]，作如下操作：

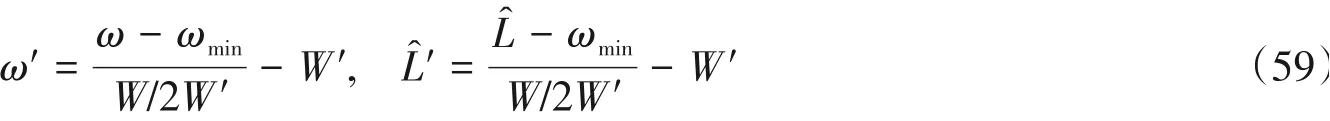
其中，W=ωmax-ωmin，

将式（60）代入式（58），可得到与在零温度下相同的表达式［参见3.4节中式（34）］，其中Chebyshev矩满足三项递推关系：

5 应用

自1995年Hallberg［17］提出Lanczos DMRG求解一维Heisenberg模型的自旋关联函数以来，频域空间的DMRG算法逐渐发展，并被广泛应用于电子体系（Hubbard模型及其扩展、Anderson杂质模型、从头算量子化学哈密顿量）、电-声子体系（Holstein模型）、自旋体系（Heisenberg模型）等不同体系响应性质的计算.下面将从电子问题以及电声子耦合问题两个方面介绍其代表性的应用场景.

5.1 电子问题

无机半导体一般具有较大的介电常数ε＞10，因此对于固相下的分子间库仑相互作用可以实现很好的屏蔽，故常用单电子的能带模型.然而，对于有机半导体而言，分子间的相互作用力以相对小的范德华力为主，一般具有较小的介电常数（ε约为2～4），对于分子间的库仑相互作用不能较好地屏蔽，体系经光激发产生的电子-空穴对（激子）的结合能较大，激子相对局域，半径较小.扩展的Hubbard-Peierls模型是考虑电子-空穴之间的吸引势的一种简单处理方式：

式中，t为最近邻跳跃积分；δ为调节键长的参数，描述了Peierls不稳定性.如对于聚乙炔链来说，双键对应的跳跃积分为t（1+δ），单键对应的跳跃积分为t（1-δ），U为占位库仑排斥，V为最近邻的库仑势，如图9所示.

基于此哈密顿量，Pati等［8］研究了不同长度的链在不同参数下的三阶非线性极化率，见图10.3.2节已经介绍了基于CV-DMRG如何求解线性响应性质，尽管非线性响应的表示更为复杂，但仍可采用CV-DMRG在同一框架下进行计算［5，8］.

Fig.9 Representation of extended Hubbard-Peierls model

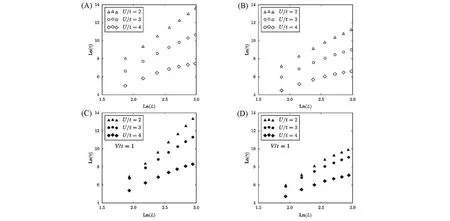
Fig.10 Plot of the log of average third-order polarizability log of the chain length L[8]

Jeckelmann［21］基于CV-DMRG方法提出了DDMRG方法，并通过计算流-流关联函数计算上述模型在不考虑近邻电子关联（V=0）时的光电导谱（见图11），当再忽略式（62）中的Hubbard项（U=0）时，此哈密顿量描述了自由电子体系，因此其光电导率可以精确求解，由图11（A）可见，基于DDMRG的结果与精确解完全重合，印证了该方法的精确性和有效性.图11（B）描述了对于Mott-Hubbard模型、Peierls模型以及Hubbard-Peierls模型3种不同参数条件下的光电导率.

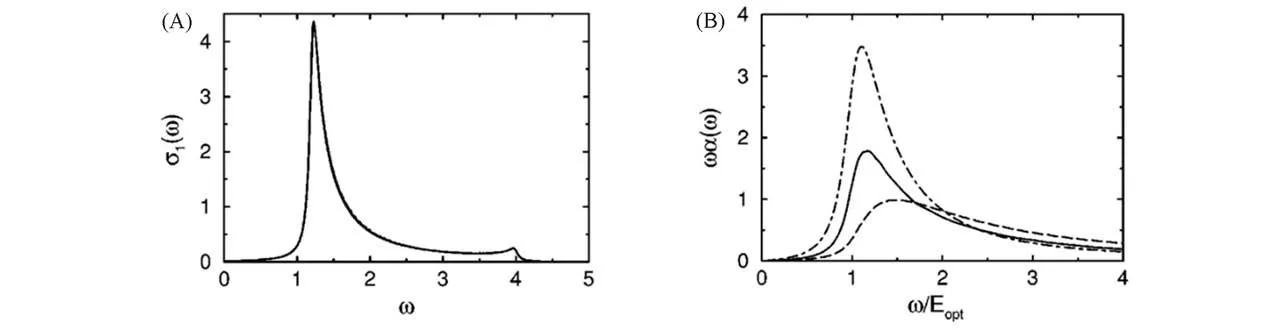
Fig.11 Optical conductivity calculated by DDMRG［21］

Chan等［25］发展了解析的线性响应DMRG方法，通过计算聚乙炔的极化率，将其与DDMRG方法进行了比较.对于较小的M（如25）时，DDMRG在某些情况下误差较大，甚至达到了50%，相比之下，解析线性响应DMRG的精度远远大于DDMRG，随着M的增大，两种方法都逐渐收敛，当M=250时，DDMRG的结果略优于解析线性响应DMRG.此外，Chan等［14］将DDMRG应用到一维氢链模型以及Hubbard模型，通过求解单电子格林函数得到光电子能谱，以FCI的结果为基准比较了DDMRG与TDDMRG的表现，如图12所示，随着M的增大，两者均逐渐收敛到FCI的结果，DDMRG明显收敛速度更快，此外，他们还将DDMRG用于精确计算水分子中O1s轨道的核电离能.

Fig.12 Dependence ofthe local density of states at the central site of a hydrogen chain(N=10)with different bond dimensions[14]

5.2 电声子耦合问题

对于π电子共轭的有机分子聚集体系的能量转移与电荷转移常常伴随着核的运动，其光电响应性质从而受到电声子耦合的影响，当电声子耦合比较弱时，基态可以考虑为在被声子云“缀饰”的接近自由的电子的图像，当电声子耦合比较强时，晶格畸变导致电子自陷而形成了一种准粒子，也被称为极化子.White等［43］基于Lanczos DMRG研究了Holstein模型中电声耦合强度对于电子运动的影响（图13），图中γ为第i个格点对应的电声耦合强度，t为最近邻格点的跳跃积分.该图展示了与光学电导率相关的部分物理量随电声耦合强度γ的变化.对于光学电导率有σ(ω)=Dδ(ω)+σ′(ω)，D来源于光电导率的Drude峰，对应于光电导率相干项的权重，σ′(ω)对应于非相干项的权重.在图13（A）中，T为每个格点上的平均电子动能，并与σ(ω)存在的关系，即T刻画了光电导率的总权重.当电声耦合强度γ=0时，非相干项σ′(ω)对于光电导率的贡献为0，存在D=T的关系，即对应于无相互作用的自由电子系统.随着γ的增加，D与T均下降，D下降得相对更快，且在γ＞2t时变得很小，光电导率的相干项的贡献（D与T的比值）逐渐减小，即非相干项比重增大，由于电声相互作用的增强形成了局域的极化子.从图13（B）也可见，在极化子范围内（γ=2.5t），谱的形状更为复杂.

Fig.13 Dynamical properties of Holstein model[43]

最近，我们［22］基于MPS/MPO的框架给出了零温度及有限温度下的DDMRG算法，并通过计算偶极-偶极关联函数得到分子聚集体的吸收、发射光谱，该算法已在DMRG开源程序Renormalizer［58］中实现.Holstein模型被用以描述同时存在分子间激子耦合与分子内电子-振动相互作用的体系如下：

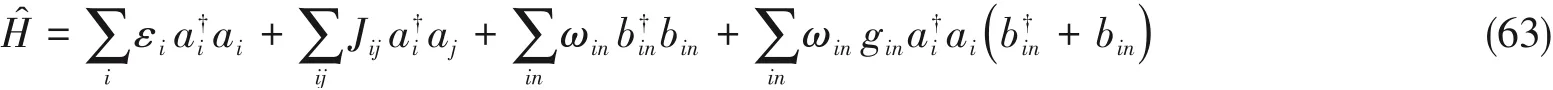
式中，εi为第i个分子的绝热激发能；Jij是第i，j个分子之间的激子耦合；ωin与gin分别为第i个分子的第n个谐振子振动模式的频率以及对应的电声耦合系数，如图14所示.

图15给出了DDMRG计算分子二聚体的吸收、发射强度在不同的参数空间的误差（以精确对角化结果为标准），并与此前发展的高精度含时密度矩阵重正化群（TD-DMRG方法）［15］进行了比较.

该二聚体模型体系带有一个频率为ω0的简谐振动模式（16个振动能级），选取了不同的激子耦合J=±ω0（H/J聚集体），不同的黄昆因子S=g2以及不同的温度kBT∈[ω0，2ω0，4ω0]进行研究，对于DDMRG及TD-DMRG的计算采用了同样的Lorentz展宽η=0.1ω0.在给定M=120的条件下，DDMRG的误差在整体的参数空间均小于TD-DMRG，尤其是在低温区达到了近乎精确的结果，但其误差随着温度升高而上升，这是由于在高温下存在更多的态之间跃迁，这对于CV的截断是不利的，需要保留更大的维数（M）来达到更高的精度，因此DDMRG更适合于计算低温区的响应性质.需要指出的是，对于大量的有机共轭分子存在着ω0在1400 cm-1的振动序列（Vibronic progression），在室温下处于kBT≤ω0的区间.在此之前，n粒子近似作为一种经济有效的方法被成功应用于一系列光谱性质的理论研究［59］，将DDMRG与n粒子近似进行了比较，以揭示n粒子近似的适用区间.图16比较了双粒子近似（2-PA）与DDMRG在3种不同的激子耦合强度下的不同温度下的0-0发射峰的强度，可见双粒子近似对于相对弱的耦合与较低温度下可以给出令人满意的结果，但在较高温度与强激子耦合条件下表现较差，只考虑双粒子近似不足以描述较大的极化子.进一步探究了0-0发射峰与激子相干长度的关系，发现在3种不同耦合情况二者都几乎呈线性关系.针对可进行精确对角化的五聚体体系（最近邻作用），比较了n粒子近似方法与DDMRG的误差，由图17（A）所示，当kBT=ω0时，双粒子近似约存在30%的高估，最简单的单粒子近似计算在kBT=ω0时具有相当大的误差，使用M=50，DDMRG便实现了与4粒子近似相当的精度，此外，图17（B）展示了kB=ω0时的发射强度.

Fig.14 Graphical representation of molecular aggregates characterized by Holstein model

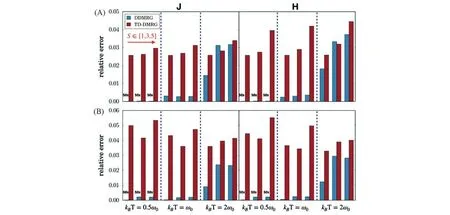
Fig.15 Relative error for J-and H-aggregates with different Huang-Rhys factor（S∈[1.0，3.0，5.0]）across different temperature（kBT∈[0.5ω0，ω0，2ω0]）［22］

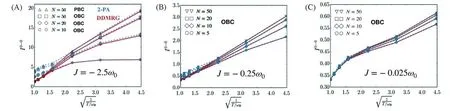
Fig.16 0-0 emission strength I0-0 as a function of T-1/2 for different excitonic coupling J0(A linear relation between them is predicted by strong excitonic coupling perturbation theory[59])[22]

作为一种新的频率空间的响应计算方法，CheMPS在电子-振动耦合体系的应用仍未曾有探索，在这里，我们首次将CheMPS应用于计算Holstein模型在零温度以及有限温度下的吸收光谱，展示该算法的主要特点，并做出相应的讨论.以每个分子带有一个频率为ω0的振动模式（振动能级数为16）的二聚体为研究对象，图18给出了利用CheMPS在系统总的能量空间下计算的零温度以及有限温度（kBT=ω0/2）时的吸收光谱S(ω)［式（15）和式（53）］.为了将其与DDMRG进行比较，首先利用Lorentz系数［式（33），λ=4］对于给定的Chebyshev矩的个数N（即演化的步数）得到其在频率ω处相应的Lorentz展宽（详见3.4节），而后进行在该展宽下的DDMRG单个频率计算.CheMPS与DDMRG在零温度以及有限温度在同样的M下实现了很好的吻合（且两种方法的结果均关于M收敛）.图19展示了不同的演化步数N得到的吸收光谱，根据在3.3节中提到的Lorentz展宽演化的步数N的关系（展宽与演化的步数呈反比），CheMPS方法可以通过调整演化的步数精确地调控光谱的精细程度.

Fig.17 Comparison between DDMRG and n-particle approximation［22］

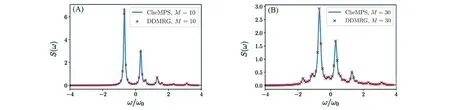
Fig.18 Linear absorption spectrum（omit the pre-factor of the frequency index）of dimer model using CheMPS and the comparison with DDMRG

图18所示的光谱所在的频率区间只占了系统能量空间的一小部分，由图19可见，在相当大的能量范围内是没有吸收强度的.根据3.3节提到的Lorentz展宽与实际计算时被投影的频率区间宽度的关系，宽度越大，为了达到相同的Lorentz展宽就需要演化更多的步数.对于我们在本文研究的Holstein模型而言，系统的能量区间的最大值是激发态的能量最高点与基态的能量最低点的差值，在模式较多或振动能级数较高的时候，如此高能态的振子强度几乎为零，我们实际关心的光谱范围将远远小于系统总的能量区间.因此，不将系统的整个能量区间投影到［-1，1］之间，而是选取一个有效的能量区间W*（W*＜W），尤其是对于考虑电子-振动耦合系统的光谱将大大减少所需演化的步数.

Fig.19 Linear absorption spectrum using different numbers of Chebyshev moments for expansion

图20展示了当选取的有效能量区间W*为系统的总能量区间W的一半时的零温度的吸收光谱，并将其与选择总能量区间W直接计算的结果进行了比较.当选择的有效能量区间W*＜W时，确实可以用较少的演化步数得到同样的精细程度（见图20的蓝线）.然而，对于同样选取W*=W/2，如果不做能量截断，在演化到N=70时便发散了（见图20插图）.随着演化的继续，选取有效能量空间W*的方案会产生误差（见图20的红线），这与Krylov子空间的维度dk与扫描圈数ns有关，图21展示了不同的dk与ns计算光谱的相对误差，可以发现，dk与ns对于误差的影响均不是单调的，因为截断是局部进行的，因此可能会存在“欠截断”与“过截断”的效果.说明选取怎样的有效能量空间W*，多大的dk与ns是没有明确的准则去遵循的，而且其最优组合将视不同体系决定.

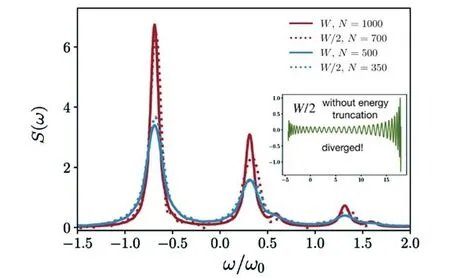
Fig.20 Linear absorption spectrum calculated by using effective frequency window and the energy truncation scheme with the Krylov subspace dimension dk=10 and ns=1 sweep times

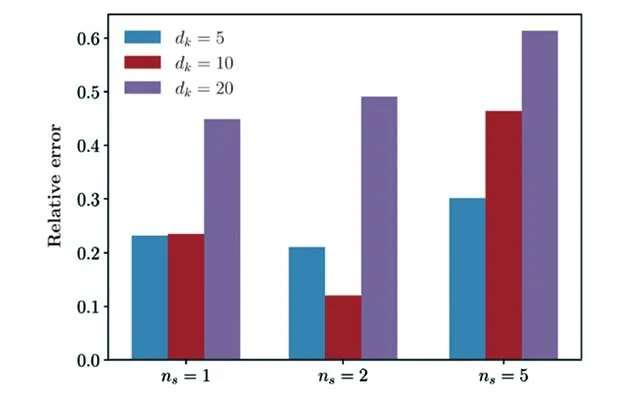
Fig.21 Relative error using effective band(W*=W/2)at N=700 with respect to the full many body band calculationat N=1000 for different combinations of Krylov subspace dimension dk and sweep times ns for energy truncation

6 总结与展望

DMRG作为一种计算低维强关联体系电子结构的方法，近20多年来已经逐渐地成为量子化学的重要计算手段.对于电子结构问题，DMRG可以作为CASSCF中取代Full CI的求解器，从而使得可处理的活性空间远大于传统的方法.近几年，随着含时DMRG和响应理论的发展，已迅速发展成为计算复杂体系量子动力学和光谱的高精度方法.求解响应性质有两种不同的角度：（1）直接在频率域求解响应函数；（2）通过时间演化得到时间关联函数，并通过傅里叶变换得到频率域的信息.本文详细阐述了频率空间的几种不同的算法，并介绍了其应用.DDMRG的优点是可以实现大规模的并行计算，即每个频率的精确计算都是独立进行的，最后收集起来就得到了整个频域的谱线.对于只需计算少量点的响应性质计算的时候，DDMRG将是首要的选择.CheMPS尽管也是一种频率域的计算方法，但其可以一次性得到所有频率的响应信息，因其更为快速，将CheMPS首次应用到计算电声子耦合系统的响应性质，展示了该算法的主要特点以及进一步探索的方向，如果系统有响应信息的频率区间占整个系统的能量空间的绝大部分，CheMPS将是一种兼顾精度与计算量的计算方法，如果有响应的频率区间只占了整个系统的能量空间的一小部分，可以在有效的频率空间进行展开，同时需要做能量截断，这可以大大节省演化的步数，然而一种高效的、可靠的能量截断方案有待进一步的探索.电声耦合体系拥有较大的系统能量空间，尤其是对于多分子、多模式与振动能级高的情况，需要探索一种高效的、可靠的能量截断方案.

TD-DMRG作为一种数值精确的方法被广泛用于超快动力学的计算，相较于频率空间的方法，TD-DMRG可以给出实时动力学信息.此外，TD-DMRG可以一次性得到整个频率空间的响应性质.TD-DMRG的弱点在于长时间演化，首先在演化的过程中存在误差的累积，另外，由于系统的纠缠随着时间增加，为了获得相同的精度，所需的M应随时间增加而变大［33～35］.频率空间的方法可以避免这一问题，有望给出更为精确的结果.在频率空间算法中，CV-DMRG以及其衍生算法DDMRG算法需要对每一个频率分别进行计算，具有非常高的精度，但是存在计算速度慢的问题，但可以利用其天然并行的优势以及通过GPU加速张量计算［22］大大缩短计算时间.

借助于热场动力学（纯化）的方法，响应性质的计算被自然地推广到有限温度.热场动力学方法以无穷高温度下的最大纠缠态作为演化的初态进行虚时演化，因此对于较低温度需要演化更多步，最小纠缠典型量子热态（Minimally entangled typical thermal states，METTS）方法［60］是对于热场动力学方法在T→0的低温计算的有力补充.

近几年的发展也表明，DMRG方法尤其是其矩阵乘积态的理论形式除了作为一种解决电子相关问题的有效方法，也是一种高效、准确的复杂体系量子动力学和光谱计算方法，这方面的研究还处于初始阶段，大量的探索性工作有待开展，本文所涉及频域的动态DMRG代表着一种探索，将在更多的应用实例中得到发展.