基于改进粒子群优化的快速目标定位*

2020-12-23敖佳，陈蔓

通信技术 2020年12期

敖佳，陈蔓

（中国电子科技网络信息安全有限公司，四川成都 610000）

0 引言

随着信息技术的不断发展，计算机视觉在制造业领域发挥着重要作用[1]。图像目标定位作为其中的一个分支，是该领域的研究热点。制造业领域产品的图像采集具备连续性、重复性等特点，若对采集的图像进行分割则需使用模板图像进行定位。此过程也可抽象地看作目标跟踪。由于工业制造过程具有实时性要求，因此目标跟踪过程的目标定位需快速且准确。

目标定位可以看作是目标搜索过程的优化，以达到快速搜索的目的，从而满足实时性要求。搜索过程的优化可以采用确定性方法或随机方法。在确定性方法中，具有代表性的是均值漂移[2-3]和Snakes 模型[4]。随机方法中具有代表性的是卡尔曼滤波法[5]和粒子滤波法[6-7]。随机方法通常速度很快，但是容易陷入局部最优，因为它们依赖迭代搜索来寻找模板图像和当前图像之间代价函数的局部最优值。

粒子群优化算法[8]是一种随机优化技术。由于它的实现简单且已成功应用于各个领域[9-11]，因此受到了人们的广泛关注。过去十年内，较多学者在其基础上进行了相关改进，或针对静态或针对动态的优化问题，均取得了较好的结果。粒子群算法也成功应用于目标定位[12-15]，如Borra[13]等提出的模糊均值分类粒子群算法（Particle Swarm Optimization Fuzzy Means Clustering，PSO-FMC）。PSO-FMC 使用混合图像分割方法和模式匹配，其中图像分割采用模糊C 均值聚类分离目标，然后进行模式匹配。该方法较耗时，且其精度极大地依赖于图像分割的精度。

本文提出一种基于改进粒子群优化的快速目标定位算法，对粒子群算法做出了两方面点改进。一方面，对粒子的初始化范围进行区域划分，使粒子初始化位置分布相对均匀，一定程度上加快了收敛速度。另一方面，引入采用“猎物-捕食者”机制的粒子群优化算法[16]，通过删除或转换“懒惰”粒子进一步加速算法收敛，提高计算效率。实验结果表明，本文提出的算法在收敛速度和稳定性方面均有一定提升。

1 粒子群算法

Kennedy[8]等提出的粒子群优化算法（Particle Swarm Optimization，PSO）受到了鸟群觅食行为的启发，即模拟鸟群寻找食物源。如果对鸟群的觅食行为进行建模，那么种群中的粒子则被认为是给定问题的解，而问题的解空间是粒子为了寻找问题最优解可活动的范围。粒子活动时存在两个关键点，一是全局最佳粒子，二是该粒子的历史记忆，即该粒子活动过程中的当前最佳解。每个粒子具备位置和速度两个基本属性。位置和速度在粒子活动的整个生命周期中不断迭代更新，更新公式为：

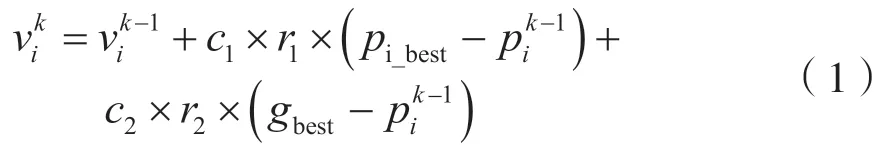
2 本文算法

本文提出一种基于改进粒子群优化的快速目标定位算法，主要包括5 个步骤。

2.1 粒子初始化

粒子的初始化包括位置和速度的初始化。由于本文针对的是图像目标的定位，因此速度初始化为[-1，1]之间的随机数。位置为二维，相对于所有粒子位置均随机初始化而言做出了如下改进：将搜索目标范围等分为4 个子区域，同时将粒子也等分为4 份（若无法等分，最后一个区域可多或少部分粒子），随机初始化到对应的4 个子区域范围内；搜索范围的正中心初始化一个粒子，若初始化粒子数n=17，则图1 为其可能的初始分布之一。

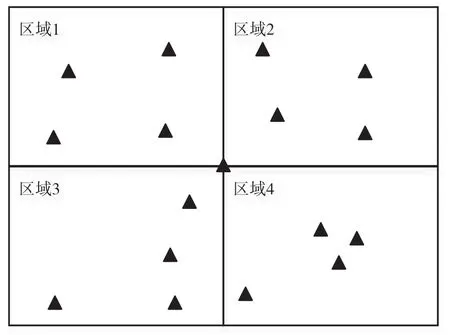
图1 粒子位置初始化（n=17）

每个区域初始化粒子数可公式化为：

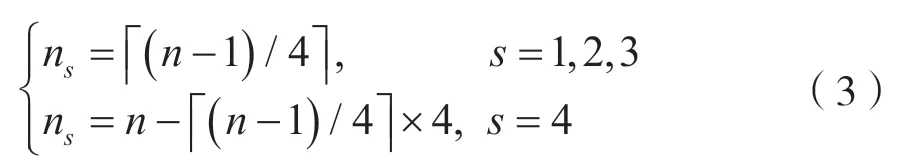
式中，ns(s=1,2,3,4)为区域s内的粒子数。

2.2 种群评估

种群评估共包含3 个部分。

第1 部分：计算每个粒子的适应度。本文针对的是图像目标的定位，因此粒子的适应度为目标与图像部分位置的相似度。相似度越高，匹配程度也越高。相似度公式表示为：

式中，fitness(i)为粒子i的适应度，pi_x,pi_y分别为粒子i在x方向、y方向的位置，f为相似度计算函数。本文使用以该点为中心的邻域矩阵相关性表示，相关性计算公式如下：

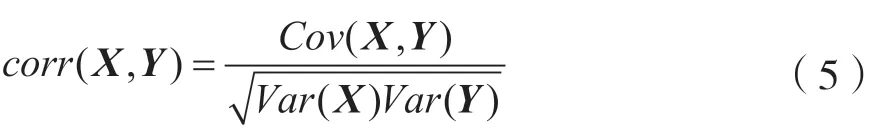
式中，corr(X,Y)为X、Y的相似度，X、Y为二维矩阵，Cov(X,Y)为X、Y的协方差，Var(X)、Var(Y)分别为X、Y的方差。

第2 部分：计算每个粒子当前时刻的最佳位置。比较粒子当前时刻位置与历史最佳位置的适应度，如果当前时刻位置的适应度更大，则更新该粒子的最佳位置为当前位置，并同步更新最佳适应度。

第3 部分：计算全局最佳粒子。将粒子当前时刻位置的适应度与全局最佳粒子适应度进行比较，若大于它，则更新全局最佳粒子的位置和适应度。

2.3 信息更新

信息的更新包括各粒子速度和位置的更新，本文针对的是二维情况，因此速度和位置的更新公式为：

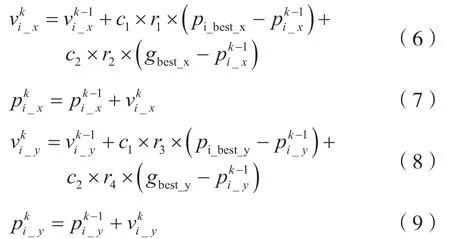
2.4 猎物和捕食者关系

“懒惰”粒子是指速度很低、对寻找最佳位置贡献度不大的粒子，因此需设置一个速度阈值E，判定哪些粒子为“懒惰”粒子，具体处理流程如图2 所示。

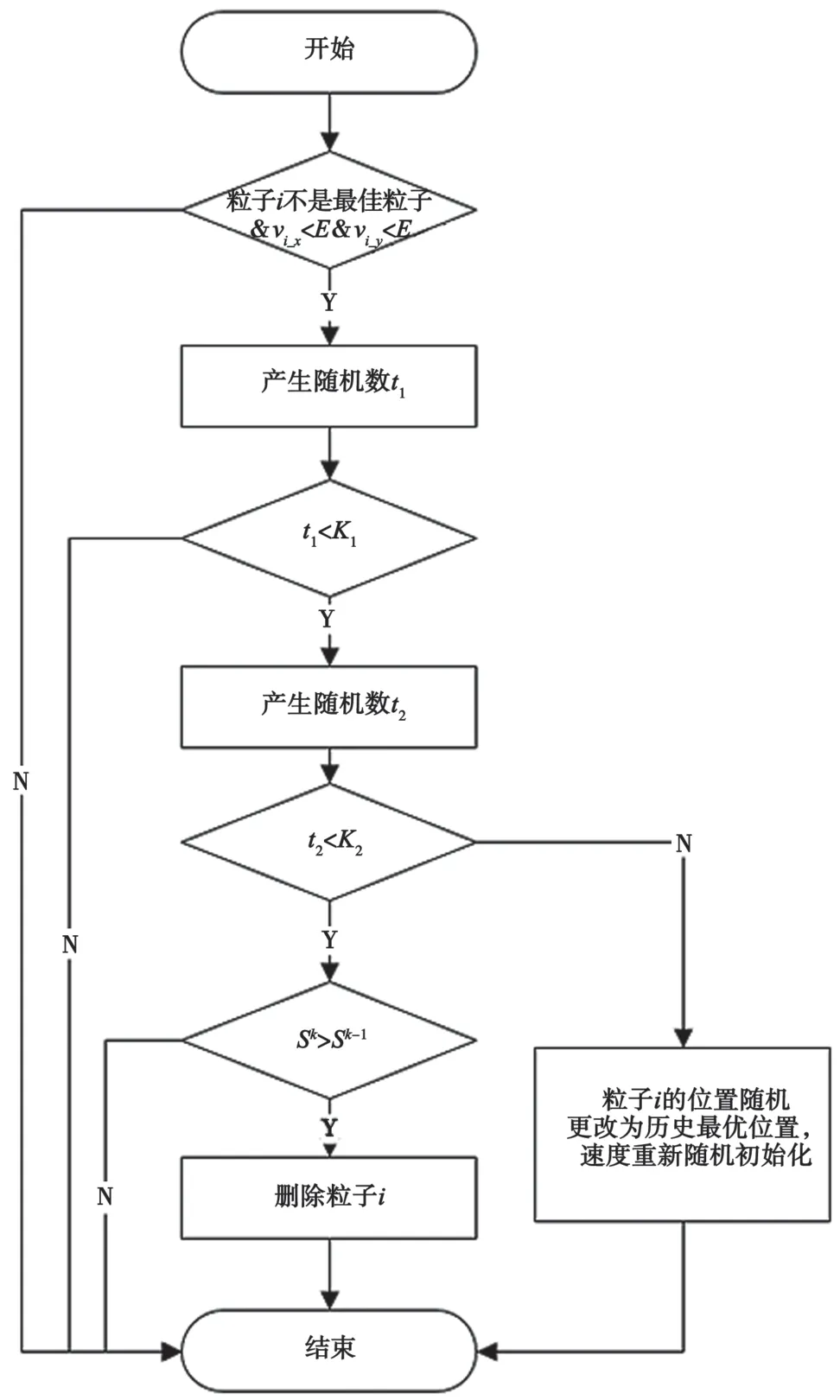
图2 猎物-捕食者关系流程

步骤1：如果粒子i不是全局最佳粒子，且粒子的速度小于速度阈值E，则判定为“懒惰”粒子，并转步骤2。

步骤2：产生一个[0，1]之间的随机数t1，并设置一个阈值K1，K1表示猎物（当前粒子i）遇到捕食者的概率，若随机数t1＜K1，粒子i的行为将转到步骤3。

步骤3：产生另一个[0，1]之间的随机数t2，并设置一个阈值K2，K2表示猎物被捕食者抓住的概率，如果t2＜K2，将转到步骤4（表示被抓住），否则转到步骤5（表示猎物成功逃脱）。

步骤4：如果当前种群大小S大于上一次迭代时的种群大小，直接删除当前粒子i。

步骤5：当前粒子i的位置将随机更改为其历史最优位置，粒子i的速度则重新随机初始化。

文献[16]对K1、K2进行了相关实验，并给出了其最佳变化范围。K1变化范围为[0.3，0.5]，K2变化范围为[0.1，0.2]，本文取K1=0.4，K2=0.1。

2.5 种群繁殖

种群数量的波动需要控制在一定的范围之内，可使用比例积分（Proportional-Integral，PI）控制方法。PI 控制可以稳定有效地将参数控制在某个指定范围内，或控制其根据某个指定的规则变动。种群数量的变化公式如下：

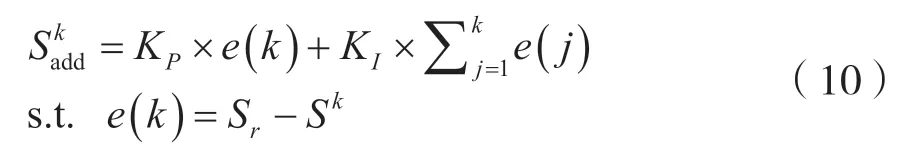
3 实验结果分析

3.1 实验数据和参数设置

为验证算法的有效性，本文随机选取了4 组实验数据[17]（来自Pascal VOC 2007），见图3，并与标准粒子群算法[8]（Standard Particle Swarm Optimizer，SPSO）、几何粒子群算法[18]（Geometric Particle Swarm Optimizer，GPSO）、自适应合作粒子群算法[19]（Adaptive Cooperative Particle Swarm Optimizer，ACPSO）以及基于基因学习的粒子群算法[20]（Genetic Learning Particle Swarm Optimizer，GLPSO）等基于粒子群的算法进行对比分析。

图3 中左边图为目标搜索源图像，右下角为待搜索目标图像（对应源图像的方框位置），右边图像为搜索目标与搜索源图像的相关性图像。显然，相关性为1 的地方，即为最终目标解。

初始粒子个数的设置会影响计算时间和迭代次数，粒子个数越多，迭代次数越少，易收敛，但会增加计算时间；反之，粒子个数越少，计算时间短，但迭代次数会增加，不利于收敛。因此，为达到计算时间和收敛稳定性之间的平衡，本文对初始粒子数做了以下实验（见图4），最终取一个相对合理的值。为实验方便，初始粒子个数取值范围在[10,100]，取值间隔为10，实验图像大小为372×372（实线）和800×800（虚线）。

图4 中带圆圈的曲线为算法运行1000 次（下同）的平均计算时间，带三角形的曲线为找到最优解的平均迭代次数，带正方形的曲线为找到最优解时迭代次数标准差（所有数据除以最大值进行归一化）。从图4 可以看出，随初始粒子数不断增加，计算时间、迭代次数均值和标准差基本在n=20 的时候出现拐点，因此本文粒子数初始化为20（若需要提高稳定性，可增加初始化粒子数量）。

图3 实验数据

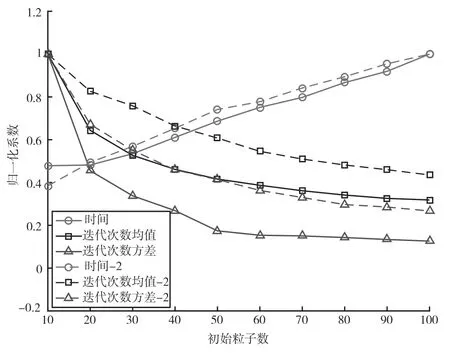
图4 计算时间与迭代次数关系

3.2 实验环境

本文实验采用的系统为Windows 7，处理器为Intel（R） Core（TM） i7-6700 CPU@3.40 GHz，内存大小为16 GB，编程环境为Matlab 2016a。

3.3 实验结果

实验结果分成两个部分：一是验证改进的粒子位置初始化方式对收敛速度的提升；二是验证算法整体在计算时间和收敛速度方面的提升。本文用到的评价指标有迭代次数均值（Mean）、迭代次数标准差（Std）、成功率（Sr）和计算时间（Time）共4 类。

3.3.1 验证改进的粒子位置初始化对收敛速度的影响

对4 组实验数据分别采用不同的初始化方式，运行传统PSO 算法1000 次，统计迭代次数的平均值和标准差。迭代次数平均值越小，说明收敛越快；迭代次数标准差越小，说明算法越稳定，实验结果分别见图5 和图6。

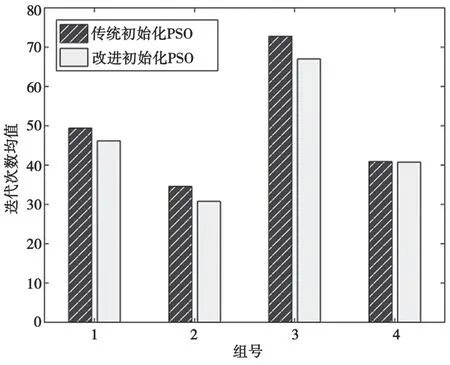
图5 迭代次数均值

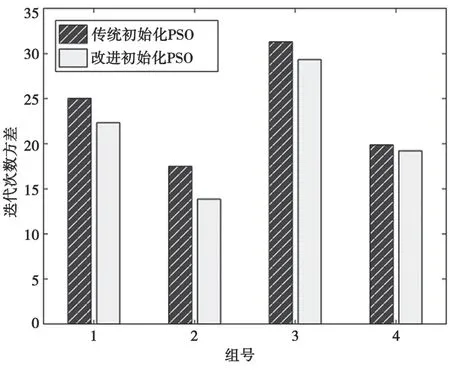
图6 迭代次数标准差

从图5 中可以看出，采用本文提出的位置初始化方式使迭代次数有了一定程度的降低，且每组实验数据均呈现出一致的趋势，说明本文提出的初始化方式能够一定程度地提升收敛速度。此外，从图6 可以看出，迭代次数标准差也相应地有所降低，说明在提升收敛速度的同时，还提升了一定的稳定性。

3.3.2 验证整体算法

对4 组实验数据分别采用3.1 节的4 类对比算法和本文提出算法，并从平均迭代次数均值、标准差、成功率和计算时间4 个方面进行分析。每类算法在每组实验数据上运行1000 次，最大迭代次数为200（若算法迭代次数超过最大迭代次数，则认为失败），实验结果见表1（加粗部分表示最优结果）。

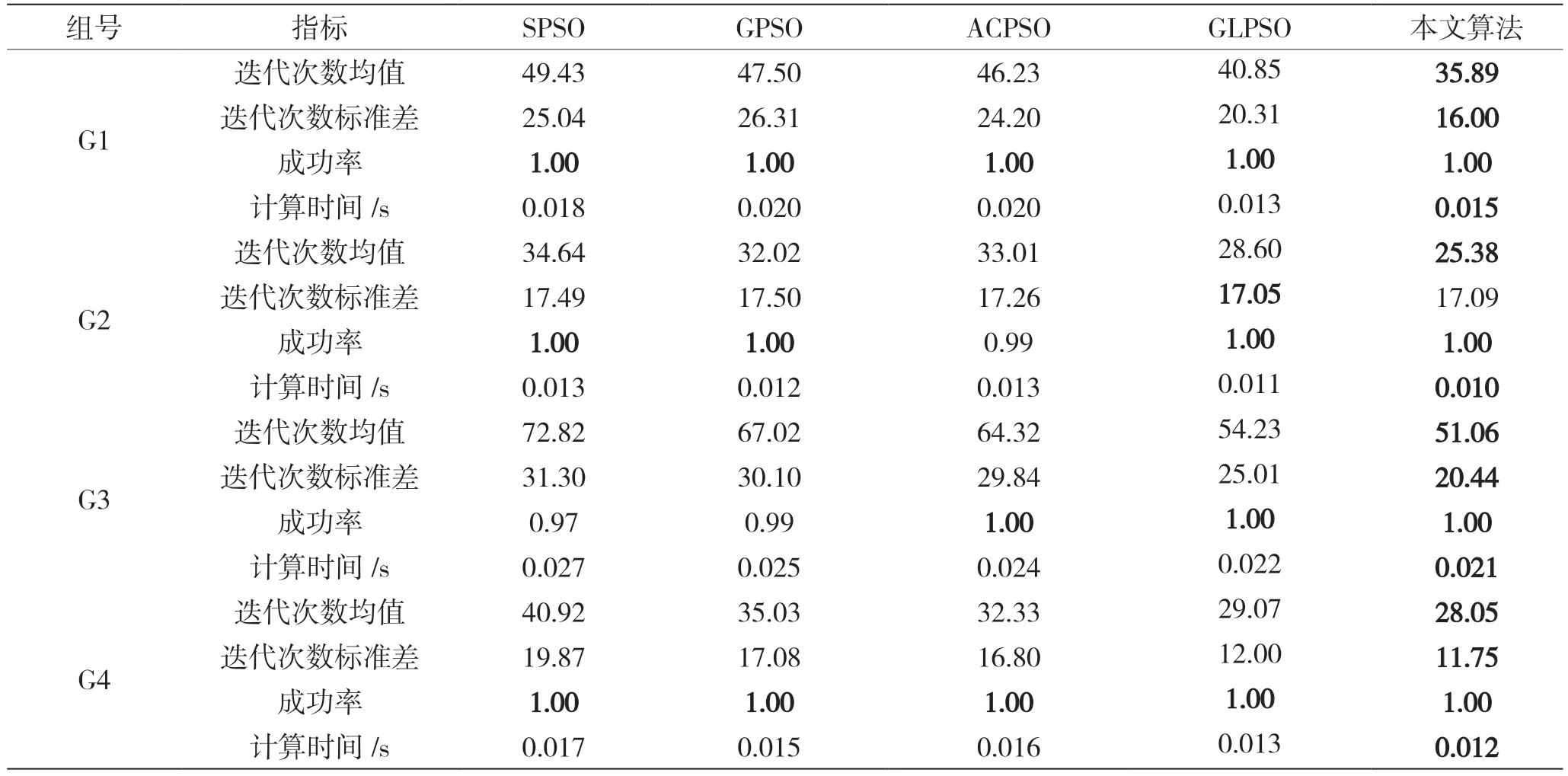
表1 实验结果

从表1 可以看出，SPSO、GPSO、ACPSO 可能出现不收敛的情况（成功率小于1.00），而GLPSO和本文算法则表现较好，在每组数据上运行1000次的情况下未出现不收敛的情况。此外，本文算法迭代次数的均值和标准差除了G2 的标准差未取得最佳结果外，其他均具有优势。此外，相对标准粒子群优化算法而言，本文算法取得了相对明显的提升，进一步说明“猎物-捕食者”机制的引入对整体算法的效果从收敛速度和稳定性方面有明显提升。