一种改进的卫星通信信号识别方法研究*

2020-12-23闫晓峰吴治霖

通信技术 2020年12期

闫晓峰，吴治霖，熊刚

（1.海军装备部，四川成都 610036；2.中国电子科技集团公司第三十研究所，四川成都 610041）

0 引言

随着通信技术的迅猛发展，卫星信号传输系统已经成为信息通信中的重要组成部分，发挥着枢纽作用。卫星通信信号在各领域得到了广泛运用，包括导航测控、信息广播、通信中继、地球遥感和军事侦察监视等。由于网电空间环境的日益复杂和干扰信号的增加，开展卫星信号识别研究具有迫切的意义，可以实现频谱监管、电磁干扰识别和空间电子对抗等方面的应用。信号识别的目的是根据不同类型信号的特征进行分析，从而判断出待识别信号的类型，也是后续完成解调分析的参数前提。据报道，2007 年美军研发了一种称作地面威胁智能识别的系统（Intelligent Surface Threat Identification System，ISTIS），可利用信号的调制特征进行目标分类。经过多年的积累，它的调制识别技术更成熟更实用化。因此，美国防高级计划研究局（Defense Advanced Research Projects Agency，DARPA）认为调制识别是实现网电态势感知的关键，有利于从密集的电磁频谱中挖掘出更多情报信息。美国国家航空航天局（National Aeronautics and Space Administration，NASA）目前也把调制识别技术作为太空认知通信系统的重点之一，利用信号环境和时空信道参数，根据相应调制类型可达成自动接收器配置、干扰抑制等效果，从而动态优化通信链路。

在卫星通信过程中，由于传输距离长，受环境因素影响大，信道衰落较大，信噪比波动大，给卫星信号调制识别问题带来了一定挑战，已引起国内外研究人员和学者的重视[1]。基于判决理论的方法主要根据假设检验似然比和概率论得出识别结果[2]。此类方法可得到检测统计量，但需要先验知识，运算量一般较大。基于统计模式的方法需要特征提取和分类识别两个步骤，常用的特征有星座图、瞬时参量等，但有的思路须较高的信噪比（如星座图算法和瞬时参量算法等），有的思路无法区分不同阶调制信号（如谱分析法），有的思路则计算复杂度相对较高（如基于小波变换思路等）[3]。

针对以上问题，本文针对卫星信号的特点，提出了一种改进方法。该方法提取混合高阶矩特征，使得可识别的信号类型集合扩展，有利于区分各阶调制的信号，尤其适用于高阶调制的卫星信号，并结合采用前馈型多层神经网络进一步提高了分类器的性能和识别准确率，在低信噪比条件下鲁棒性仍较好。在参数设置方面，通过进行优化计算且综合考虑信道放大器等因素，增加了复杂环境中的分类效率。该方法实用性强，识别率高，无需太多先验信息，且适合密集的频谱环境，能识别多种类型卫星信号，包含BPSK 信号、QPSK 信号、16QAM 信号、64QAM 信号、16APSK 信号和32APSK 信号等。

1 信号模型分析

典型的卫星信号有DVB-S2（数字卫星广播）信号、全球定位系统（Global Positioning System，GPS）信号、跟踪与数据中继卫星（Tracking and Data Relay Satellite System，TDRSS）信号、国际海事移动卫星（INternational MARitime SATallite，INMARSAT）信号和美空军卫星控制网（Air Force Satellite Control Network，AFSCN）信号等。其中，DVB-S2 信号具有高数据传输率，已受到了极其广泛的关注。在DVB-S2 标准中，定义了QPSK、8PSK、16APSK 以及32APSK 多种调制可供选择。与传统QAM 类型相比，新型的高阶APSK 类型便于实现变速率调制，具有更高的频谱利用率，标志着卫星通信技术的进步，但也增大了调制识别的难度。此外，因为包含导频序列和报头，实际的DVB-S2 信号是非平稳信号，会导致过去一些识别算法失效，故需对信号的数学模型进行深入分析。

接收机在变频、滤波处理后得到的含噪声卫星信号数字表达式一般可表示为：

式中，A表示卫星信号幅度标量，fO表示信号的剩余频偏分量，T表示符号周期，φ表示相偏分量，g[n]表示复数形式的加性高斯白噪声，并可得出归一化的平均功率表达式为：

考虑到最具代表性的卫星信号类型，可设调制类型集合为Ω={16APSK，32APSK，2PSK，4PSK，8PSK，16QAM，64QAM}。

通常而言，达到精准的频偏估计是无法实现的，所以变换后的混合信号可表示成如下形式：

式中，*表示复数共轭，上述变换实质是将频率偏移量转化为相位偏移量，尽管时变信道中的fO可能导致z[n]在IQ 平面里出现少量的旋转。

图1 表示卫星信号传输的总体流程框图。先将接收到的调制信号送入预处理模块进行幅度归一化、滤波等处理，然后通过特征提取模块提取各种统计特征。

图1 卫星信号传输的总体流程

图1 中，FEC（Forward Error Correction）表示前向纠错编码，SRRC（Square Root Raised Cosine）表示平方根升余弦，HPA（High-Power Amplifier）表示高功率放大器，AWGN（Added White Gaussian Noise）表示加性高斯白噪声信道，IMUX（Input Multiplexer）表示输入放大器，TWTA（Traveling Wave Tube Amplifier）表示行波管放大器，OMUX（Output Multiplexer）表示输出放大器。DVB-S2 接收器的设计需要考虑卫星信道特性。需要说明的是，图1 中一系列处理过程已综合了非线性失真、相位噪声等损耗因素。

2 识别算法分析

2.1 特征提取思路分析

复数平稳随机过程的混合矩s[n]可定义为：

根据随机量均值定义，式（4）可近似转化为：

引入信号新型特征计算，可定义一系列含有s[n]或s*[n]的随机变量用于生成信号的混合矩，如下：

然后，可得出：

混合高阶矩计算能够在准平稳的条件下，使得信号有限长样本估计具有一致性，且可以提供更丰富的对角切片特征。其中，π遍历S的所有子集，B表示特定子集π内的集合，π内的集合数等于|π|。E[·]表示统计期望，Si表示在S中的第i个元素。例如，如果S={s1,s2}，则可能的子集将是{(s1,s2)}和{(s1),(s2)}。根据式（8），可得到：

若s1=s[n]且s2=s*[n]，通过式（5）和零均值随机过程，可得出：

不妨设信号频偏为0，且y[n]与z[n]都是平稳零均值随机过程，则可用上述方法估计相应的混合矩。

图2 和图3 是归一化的信号高阶矩特征图示，在图中说明了各阶矩的典型取值大小。

图2 y[n]的各高阶矩理论估计值

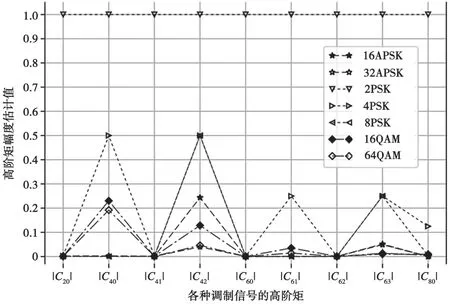
图3 z[n]的各高阶矩理论估计值

在图2 和图3 中，不同形状的线条代表不同调制类型的信号。各阶的高阶矩特征都经过了归一化处理，故其最大值等于1。根据高阶矩的性质，高斯噪声的4 阶及以上的累积量均为0，APSK 调制信号的高阶矩值与其星座图上内外圆半径比有关。

2.2 分类器思路分析

本文采取改进的识别分类器思路，此处使用的神经网络分类器模型为前馈型、反向传播的多层感知器网络结构。前馈型多层神经网络能够处理复杂的非线性计算问题。由于累积量特征参数具有不同的量纲，取值范围的差异相对较大，因此需要使用最值归一化进行基本的缩放，将特征向量值规范到0～1，也使得各维度的参数分布较均匀，提升分类过程的收敛速率和识别性能。前馈型多层神经网络模型的结构如图4 所示。

图4 前馈型多层神经网络模型的结构

该网络共3 层，输入为一个长度为10 的经过预处理的特征向量，其宽度为40，是全连接的结构。网络中激活函数采用线性整流tan 函数。该函数可起到较好的优化效果且能避免目标函数梯度急剧下降等问题。网络的输出层宽度为7（用符号Ω表示，（表示待识别的调制信号种类数目，此处与网络输出层的宽度相等），也为全连接结构，输出激活函数为归一化指数softmax 函数，即[4]：

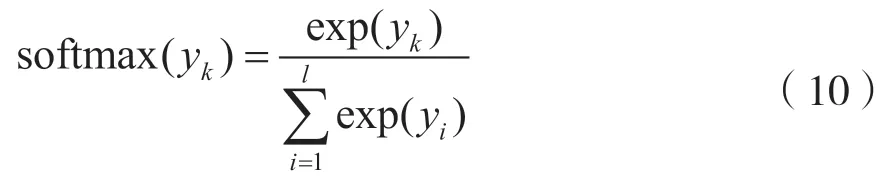
式中，yk表示该神经网络中输出层第k个神经元输出。该函数对于分类的作用是可以将输出转化为归一化的概率分布。具体分类过程中使用了一个分类交叉熵损失函数和一个Adam 优化器，再通过SOFTMAX 层输出的ARGMAX 索引来实现。

本文中改进识别分类方法的模型结构如图5 所示。该神经网络模型以一个10 元组的特征向量作为输入，并返回一个长度为7 的输出向量，其长度即调制集合的大小。调制识别结果通过输出向量的ARGMAX 索引来确定。

图5 改进方法中的神经网分类器结构

神经网络的重要设计之一即为其隐含层的设计。实际中，隐含层节点数目不能太多，否则将造成过拟合问题；但节点数也不能太少，否则将无法拟合复杂的运算模型。一般可根据经验基于网络输入及输出节点数，确定隐含层的节点数范围。训练中使用的序列长度等于由特定分类器分类的向量长度。设信号序列为r[n]，长度选取为15000 个样本点，信噪比为Es/N0，取值范围是[-3,20] dB，归一化后可转化为y[n]。通过序列加信噪比后计算得到累积量特征向量，记作(FN,y)；将y[n]转换成z[n]后得到的特征向量，记作(FN,z)。由于所有的分类步骤都经过了相同的神经网络模型进行处理，因此可以使用以下训练集作为神经网络的输入特征，进一步得到分类结果，分别为F1k,y、F2.5k,y、F5k,y、F10k,y、F20k,y、F40k,y、F80k,y、F10k,z、F20k,z、F40k,z以及F80k,z。另外，在信号捕获期间，累积量受IQ平面上星座旋转的影响，使得确定所需的最小序列长度非常重要。根据经验，当存在随机相偏时，FN,y和FN,z至少须要1000 个样本才可达到一定的识别性能。在仅能捕获到短序列样本的情况下，基于FN,z特征的分类需比基于FN,y多2 倍的数据长度就能满足对多种调制类型识别的条件。此外，在传输过程中，卫星信号通常被驱动到HPA 放大器的线性区域之外。最佳驱动电平是通过权衡放大器输出功率增加的效益与失真引起的误差来确定的。考虑放大器效应，可使用Saleh 模型进行分析，其系数来自TWTA 的实际参数。其中，Saleh 模型是用来描述HPA 非线性的典型模型。该模型的AM/AM 和AM/PM 转换特性分别为：

式中，αA、βA、αφ、βφ是模型的特性常数，r(t)表示输入幅度，A[r(t)]表示输出幅度，Φ[r(t)]表示输出的调制相位。根据计算经验，可取典型值为：αA=1.9638，βA=0.9945，αφ=2.5293，βφ=2.8168[5]。

对经过放大器的信号进行分类，可得出：由于PSK 信号仅有单一的幅度电平，因此放大器失真在归一化后只有一个相位旋转，不会受到影响；APSK 和QAM 信号则可能受放大器失真的影响，因此应将分类器的设计适应于放大处理过程，或者参数化配置放大器的驱动电平，并和累积量特征一起用作神经网络输入。考虑到所用的驱动电平特性与发射机真实驱动电平高度相关，故能提高分类识别性能。

3 仿真结果及性能分析

为验证本文新改进方法的有效性进行MATLAB仿真实验，仿真参数设置如下：采样率为100 MHz，载频为60 MHz，码速率为2.5 Mb/s，样本点数为8192，蒙特卡洛仿真次数为2000 次，噪声为高斯白噪声。采用改进思路实现卫星信号类型识别，得出正确识别率。仿真结果如图6 所示，不同曲线代表不同的类型。