极化对消算法的进一步研究*

朱胜利

（中国电子科技集团公司第十研究所，四川 成都 610036）

0 引言

近年来，随着卫星通信技术的飞速发展，通过卫星观测获得的数据也越来越大。数据量的增加导致对地数据传输的难度不断加大，传输信息所占用的带宽也越来越多。为了解决这些问题，增加系统容量，通常有两种方法。第一种是是采用更高阶的调制体制，如32APSK 和64QAM，通过增加每符号的传输比特数来增加传输速率。第二种方法是在传输信息时采用极化复用技术。由于极化复用技术的频谱利用率高，其在国内外各类遥感卫星中得到了广泛应用，如国外的GeoEye-1、World View-2 及国内的ZY-3 和GF 系列卫星[1]。

极化复用技术在使用时，容易受到实际通信环境及收发设备的影响，如非理想的传输信道、雨衰[2][3]、电离层、天线隔离度等。这些因素的影响会使得极化复用的两路独立的信号之间存在混叠，从而产生交叉极化干扰，进一步影响通信系统的性能。在使用双极化工作方式的卫星通信系统中，必须解决好极化干扰的问题。为了减弱甚至消除天线极化隔离度不足带来的残余干扰信号的影响，需要在高速解调器中采用极化对消技术。采用该技术的目的就是将主通道中的干扰信号影响消除或减弱，提升右旋信号Eb/N0，提高数据接收可靠性。

随着极化复用技术的应用，对该技术的研究也逐渐成为热点。对极化复用技术最初的研究多集中在理论层面，文献[4]利用ITU的星地链路计算模型，给出了雨衰和降雨去极化效应的影响分析；文献[5]针对极化干扰对星地数据传输系统的影响，推导星地数据传输系统极化干扰的理论值，对数据传输系统在不同的调制体制和信道编码方式下的误码率恶化情况进行了仿真，比较了在相同程度的极化干扰下不同体制传输的性能，分析了星地遥感数据传输系统所受极化干扰影响的规律；文献[6]通过对遥感卫星极化复用数据传输链路的分析，研究了交叉极化的产生及其对链路极化损耗的定量影响。

在对极化对消技术的研究方面，文献[1]提出了全数据交叉极化干扰消除器的设计方案，研制了具有交叉极化干扰消除解调功能的一体化工程样机；文献0 提出了一种基于多维搜索的极化对消方法，将影响对消算法的路径延迟、频差和初相的求解转化为三维峰值搜索问题，得到精确的对消因子，从而实现对消。实验结果验证了该算法的有效性，但由于搜索维度较大，硬件实现难度较大。

文献[8]针对高速数传信号[9]的接收特点及卫星天线极化干扰问题，提出了一种适用于高速数传解调器的极化对消方法。该方法利用主信号的解调环路信息提取对应的基带干扰信号，并通过自适应算法确定滤波器系数抵消主信号中的交叉极化干扰分量。该方法不需要估计主信号和干扰信号之间的频差就可以比较有效地对消干扰信号。且复杂度相对基带对消方法高，相对中频高速ADC 样本直接对消的方法复杂度低。

文献[10]提出了一种简单有效且易于硬件实现的极化对消方法。该方法利用辅助信号和主通道信号的相关性，并由相关系数估计隔离度，从而实现对消。由于该方法在实施时，不需要信号载波恢复和时钟同步等复杂步骤，因此更易于硬件实现。但是当相关的数据量较大时，参数估计运算量也较大。由于该方法具有易于硬件实现等优势，已于某高速数传设备中取得了广泛应用。

事实上，文献[10]中的方法既可以在解调前，AD 后实施，也可以在解调后实施，在文献[10]中，作者在解调前对该方法进行了分析，并讨论了该方法在实际中使用的有效性。然而该方法在实际使用时依然存在着相关峰无法有效锁定，对消性能差等问题。本文在考虑时延及频差对该方法影响的基础上，研究了该方法在基带和中频实施时的优劣，分析了该方法存在性能差异的原因。面对不同的调制信号，本文重点分析了噪声对该方法对消性能的影响。仿真结果表明，基于相关函数的极化对消技术在基带实施更具优势，且当主路信号和辅路信号中的噪声不同源时，利用该方法进行对消，存在一定的性能损失。

1 极化干扰信道模型

为了便于介绍基于相关函数的极化对消方法，现将常用的极化干扰的信道模型介绍如下。设通道中的主信号和干扰信号分别为x1(t)和x2(t)，则交叉极化干扰通信信道模型可以表示如下[9]：

式中，z1(t)和z2(t)分别是接收机接收到的被极化干扰的左、右旋信号；x1(t)和x2(t)分别是发射机发射的正交左、右旋信号；h11，h12，h21，h22分别是左右旋收、发天线相应的信道传输增益（函数）。

文献中一般用交叉极化隔离度（Cross Polarization Discrimination，XPD）表示主信号被干扰信号的干扰程度，设P1和P2分别表示x1(t)为主信号，x2(t)为干扰信号时以及x2(t)为主信号，x1(t)为干扰信号时的XPD。因此，P1和P2可以分别表示如下：

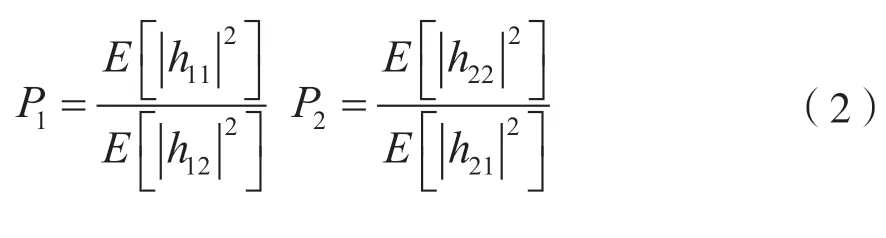
2 基于相关函数的对消算法

为了便于理论分析，本文假定存在极化干扰的信道是对称的，换言之，发射机发射的正交左、右旋信号x1(t)和x2(t)相互间的交叉极化隔离度是一样的。假设该值为λ，即P1=P2=λ。因此，极化对消的信道模型可以进一步简化如下：

实际中，由于信道噪声的存在，通道中两路信号x1(t)和x2(t)可以认为是相互独立的随机过程。其对应的相关函数可以表示如下：

由于x1(t)和x2(t)是相互独立的，即二者间相关为零，因此，上式可以进一步简化为：

由于本文针对的是常用的卫星通信信号，其调制方式一般为MPSK，其自相关函数可以归一化为一个常数E/2，也就是说[10]：R(t)=γE。

式（5）中，自相关函数R(t)可以根据输入样本来估计，而E是一个与实现无关的常数，可以归一化为1。因此，可以通过两路信号的自相关函数来估计两路信号的交叉极化隔离度γ，从而实现干扰对消的过程。基于自相关函数的干扰对消的过程可以表示为:

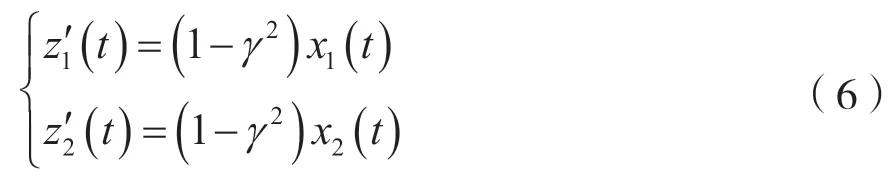
为了更加清楚地理解基于相关函数的极化对消方法，现将该方法的具体实现过程介绍如下：

（1）通过主通道信号和辅通道信号样本估计对应的相关函数，确定信号延迟；

（2）根据步骤（1）确定的延迟对齐数据；

（3）根据对齐之后的数据计算相关函数；

（4）锁定相关峰并估计γ；

（5）对消干扰信号。

假设最大相关值为Rm，则步骤（4）中γ由Rm/α来确定，其中α是一个经验值。在仿真过程中采用对称干扰模式。其中，而AdB是干扰信号相对于主信号的衰减分贝数，即XPD。

为了便于分析及讨论，在接下来的分析中，将基于相关函数的极化对消方法命名为Correlation-Based XPIC，简称CB-XPIC。

从上面的方法介绍可以看出，CB-XPIC 在计算相关函数时，理想情况下会得到两个相同的相关峰，对应两个不同通道的信号，峰值的位置可能不同。当出现两个相关峰时，由于两路信号是对称的，无法确定主信号对应的相关峰。如果没有进一步处理，则有可能存在对消错误的情况。因此，在实际中执行该方法时，会进行两次对消，并根据对消之后的信噪比大小来选择正确的结果。

3 仿真分析

本节将重点分析存在时延和相位偏差时，CBXPIC 方法在中频及基带实施的优劣。另外还较为深入地分析了噪声是否同源对对消性能的影响。

3.1 干扰存在延迟时的模型

在实际应用场景中，由于传输环境以及发射机天线等的影响，主路信号与其中的干扰信号之间总是存在时延，同时也会存在一定的相位偏差。本小节将以QPSK 为例，研究在这种情形下，CB-XPIC分别在中频和基带实施时的对消性能。下面给出干扰信号中存在延迟及相偏的极化对消模型，不失一般性，假设第一路信号中的干扰信号存在延迟及相偏：

其中φ1表示相位偏差，d表示时间延迟。则对消之后的结果为：

3.2 中频对消

仿真中，采用QPSK 信号，采样率10GHz；符号速率500MHz，载频1.2GHz，信噪比SNR=9dB，XPD 范围9～13dB，步进为1dB，去掉第一路干扰信号前面302 个采样点，主信号和干扰信号的初相均为零，在每一个XPD 下进行100 次仿真，每次仿真使用1e7 个样本点。其平均结果如图1（a）所示：

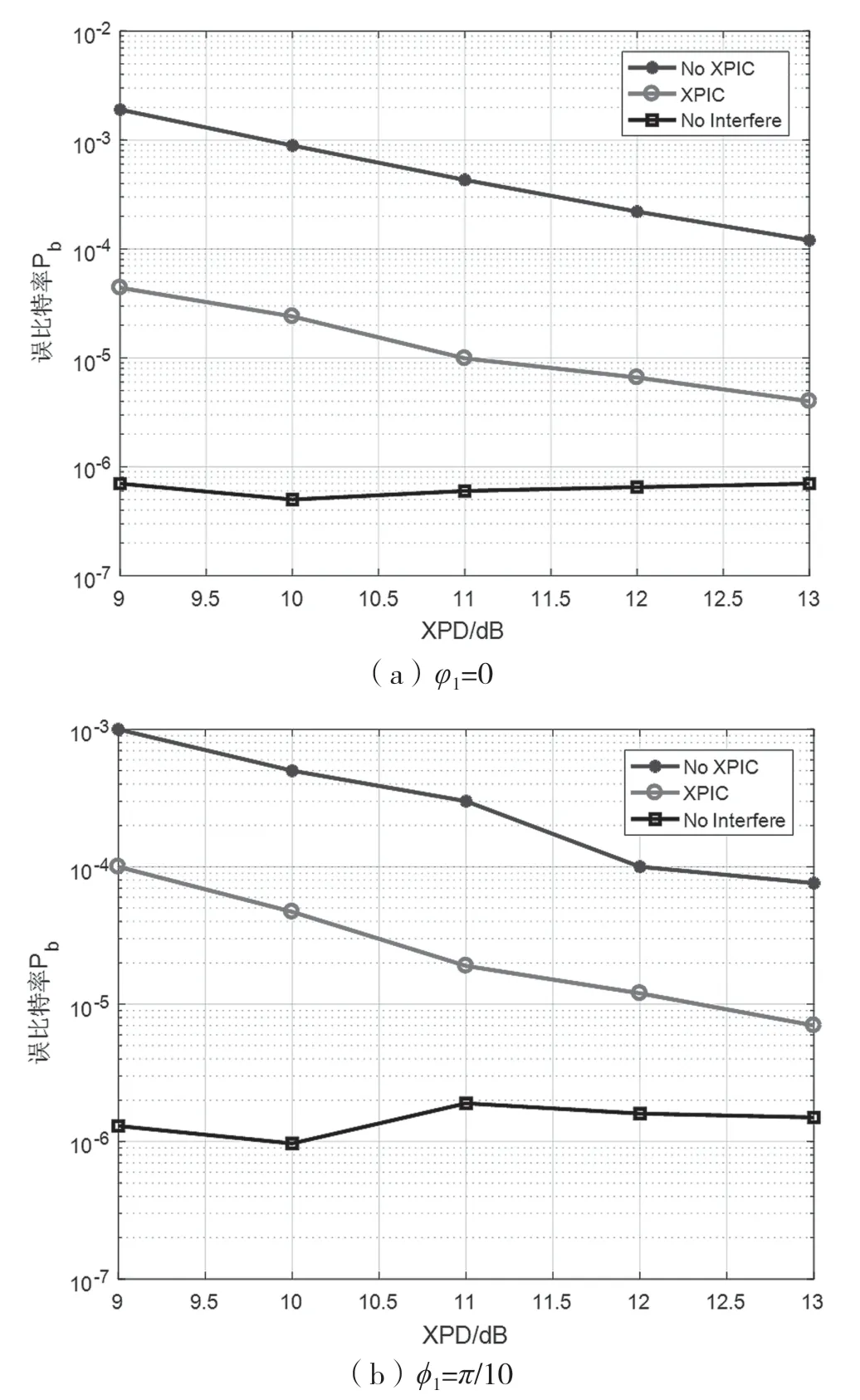
图1 干扰存在延迟时中频对消结果

图1（a）给出了不同极化对消交叉隔离度下，QPSK 信号在无干扰信号时、存在干扰信号无对消以及使用CB-XPIC 方法对消之后的误码率曲线随着隔离度XPD 的变化情况。从图中可以看出，在不同的隔离度下，CB-XPIC 方法均取得了良好的效果，且随着隔离度的增加，该方法的性能逐渐贴近没有干扰时的误码率曲线。

图1（b）给出了在其他条件不变的情况下，为第一路干扰信号添加φ1=π/10 的相偏之后所得的结果。从图1（b）中可以看出，在不同的隔离度下，对消之后的误码率曲线不同靠近没有干扰时的误码率曲线，说明CB-XPIC 方法的有效性。通过对比图1（a）和图1（b）可以发现，存在相偏时，CBXPIC 的对消性能相比无相偏时的性能有不同程度的恶化，说明主信号和干扰信号之间相偏的存在会对CB-XPIC 产生较大的影响。

从前文的分析可以知道，对于CB-XPIC 方法而言，由相关函数最大值确定的γ非常重要，该值可以通过计算相关函数的最大值，以及一个经验值α确定。由于在实际实施时，相关函数的计算是通过大量样本平滑得到的，而α是一个经验值，因此有必要对γ值在不同条件下是否发生变化进行讨论。

表1 给出了QPSK 信号在中频对消时，不同隔离度下估计值和其实际值γ的比较。对比表中第2,3 行，可以看出，当主信号和干扰信号之间不存在相位偏差时，在不同的交叉隔离度下，估计值和真实值γ的关系一致。说明利用相关函数计算的较为准确，CB-XPIC 方法能够有效对消干扰信号。对比表中第2,4 行发现，当干扰信号存在相偏时，估计值与真实值γ有一定的偏差，说明此时利用估计值对消干扰信号会有较多的干扰残余，因此CB-XPIC 方法的对消性能会有一定减弱。

表1 不同隔离度的与理论值的比较

表1 不同隔离度的与理论值的比较

图1 和表1 中的结果说明，主信号和干扰信号之间的相位偏差会对CB-XPIC 方法的性能产生重要影响。

3.3 基带对消

因为CB-XPIC 方法同样可以在基带实施，因此本小节将分析基带CB-XPIC 方法的对消性能。仿真时，主信号与干扰信号均采用QPSK 调制，其他参数设置为：数据长度1e7，过采样率10，SNR=13.5dB，隔离度范围9～13dB，步进为1dB。每一个隔离度下进行100 次仿真。仿真的平均结果如图2（a）所示。

图2 基带对消结果

从图2（a）可以看出，随着XPD 的增加，对消之后的误码率曲线逐渐贴近没有干扰时的误码率曲线，且在不同的隔离度下，对消之后的误码率曲线总是在对消之前的误码率曲线下方，说明了基带CB-XPIC 对消方法的有效性。同时，对比图1（a）和图2（a）可以发现，在没有相位偏差时，CB-XPIC在中频和基带的对消性能一致。

为了分析在基带时，相偏对CB-XPIC 方法的影响，在其他仿真参数不变的情况下对第一路干扰信号添加φ1=π/10 的相偏后继续仿真，其结果如图2（b）所示。对比图2（a）和图2（b）发现，在不同的隔离度下，基带CB-XPIC 方法几乎不受相偏的影响，表现为存在相偏时，对消之后的性能和无相偏时对消后的性能一致。

为了和基带CB-XPIC 方法进行比较，从而找到基带CB-XPIC 方法不受相偏影响的原因所在，表2 给出了不同隔离度下真实值γ和估计值以及估计值对应的绝对值之间的关系。从表2 可以看出，存在相偏及没有相偏时，尽管对γ的估计有所差异，但是，其对应的绝对值相差甚微。因此对于基带CB-XPIC 方法，尽管两路信号的相偏会导致估计值之间存在较大差异，但在忽略误差及数据量足够的情况下，它们的绝对值是一样的。

表2 不同隔离度的与理论值的比较

表2 不同隔离度的与理论值的比较

基带时，解调之后的数据比特流具有正交的形式，可以认为基带数据具有复数形式，复数的相位信息可以补偿主信号和干扰信号之间相位差带来的不良影响。而在中频时，对应的是实信号，无法提取相位信息。因此，相位偏差带来的影响无法被抵消，相位的偏差会导致相关函数估计不准确，从而导致对γ估计存在较大偏差，影响算法的对消性能。

4 误码率随信噪比的变化

前文主要研究了对消算法在时延及相位偏差等影响下的对消性能，在实际通信时信号总会受到噪声的干扰，因此研究早噪声对算法的影响具有重要意义。

仿真中采用QPSK 调制信号，数据长度1e7 个符号，过采样率10，隔离度为12dB，SNR范围8～14dB，步进0.5dB，每一个信噪比下进行200 次仿真，并去掉了第一路干扰信号的前面300 个点。干扰信号和主信号中的噪声不同源。仿真结果如图3 所示。

图3 交叉隔离度为12 时误码率随信噪比的变化情况

图3 给出了没有极化干扰、有极化干扰没有对消以及使用对消算法对消干扰时的误码率随信噪比的变化情况。从图中需要重点关注没有干扰及对消之后的误码率曲线随信噪比的变化。为了更加清楚的了解两曲线之间的关系，表3 给出了QPSK 信号不通信噪比下的误码率变化情况。

从表3 可以看出，无干扰时，当信噪比为13 时，误码率已经降为0 了，而使用对消算法后，只有当信噪比为14 时，误码率才能变为零，可以认为使用对消算法后会导致性能损失1dB。

调制方式的差异会对最终的性能损失造成一定的影响。为了和QPSK 信号的结果进行对比，图4和表4 给出了8PSK 信号在隔离度为12dB 时误码率随信噪比的变化情况。

仿真中采用1e7 个符号，过采样率10，隔离度为15dB，SNR 范围15～20dB，步进0.5dB，每一个信噪比下进行200 次仿真，并去掉了第一路干扰信号的前面300 个点。仿真结果如图4 所示。

表3 QPSK 不同信噪比下算法性能

表4 8psk 不同信噪比下的算法性能

图4 8psk 隔离度12 时误码率随信噪比的变化

图4 给出了没有极化干扰、有极化干扰没有对消以及使用对消算法对消干扰时的误码率随信噪比的变化情况。从图中需要重点关注没有干扰及对消之后的误码率曲线随信噪比的变化。为了更加清楚的了解两曲线之间的关系，表 4 给出了8PSK 信号不同信噪比下的误码率变化情况。

从表4 可以看出，无干扰时，当信噪比为18dB 时，误码率已经降为0 了，而使用对消算法后，只有当信噪比为19.5dB 时，误码率才为零，也就是采用对消算法会导致性能损失约1.5dB。

在理想条件下（无延迟，相偏等），噪声不同源时，对消前后信噪比会降低20log[(1+γ2)/(1-γ2)]dB，这种损失随着隔离度的增加而逐渐变小。同时，从表3 和表4 的结果还可以看出，调制方式不同，对消之后的性能损失不同。

在实际中，由于延迟等的存在，参考信道的干扰信号对主信道而言也是干扰，于是，信号功率会进一步下降，从而导致信噪比降低更多。

5 算法性能损失的分析

不失一般性，考虑没有延迟的情形。

（1）噪声同源时干扰模型如下：

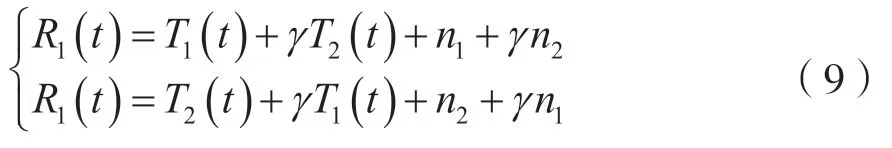
其中，n1,m1,n2,m2均是方差为σ2，均值为零的高斯白噪声序列。未加干扰前，第一路信号：R1(t)=T1(t)+n1，假设功率比为r2/σ2，对消之后有：

功率比没有发生变化。

（2）噪声不同源时的干扰模型如下：

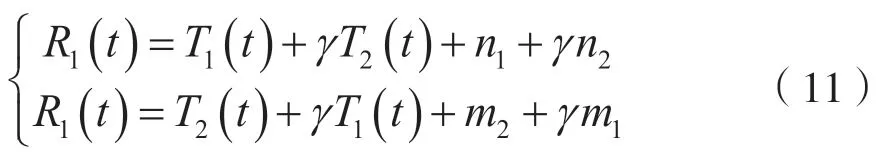
未加干扰前，第一路信号：R1(t)=T1(t)+n1，假设功率比为r2/σ2，对消之后有：

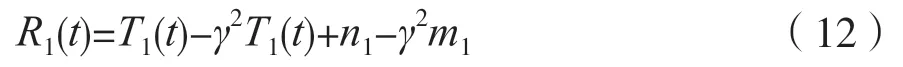
对消之后的功率比下降为：(1-γ2)s2/(1+γ2)σ2，下降程度和隔离度有关。

以上分析中并没有考虑相偏、时延等带来的影响，事实上，相偏和时延也会对对消之后的信噪比产生影响。以上分析和前面关于信噪比的仿真结果吻合。

6 结语

针对基于相关函数的极化对消方法，对比了该方法在中频实施和在基带实施的优劣，分析了存在性能差异的原因。在基带实施时，由于正交调制的原因，数据可以认为是复数，数据相关之后的虚部会对γ的估计进行补偿，相关峰更为稳定，因而不易受相偏、时延等的影响。其次，本文以QPSK 和8PSK 信号为例给出了不同隔离度下该方法的对消性能，并重点分析了不同源噪声对该方法性能的影响，给出了具体的计算方法。通过公式推导发现，如果主信号和辅助信号中的噪声是同源的，那么干扰对消之后没有任何性能损失，而如果噪声不同源，则对消之后存在一定的性能损失，该损失的多少和隔离度以及调制方式等因素有关。