一种针对全景视频编码器的复杂度优化算法

徐艺文，李玮蒙，刘 航，房 颖

(福州大学物理与信息工程学院，福建 福州 350108)

0 引言

全景视频是由多枚摄像头对当前场景从某点以不同角度进行采集后拼接得到的球面视频. 用户戴上头盔设备后，可以任意角度观看视频，从而获得比普通平面视频更佳的沉浸式体验. 为提供良好的用户体验，全景视频往往需要比平面视频更高的帧率和空间分辨率，导致视频编码器的计算复杂度急剧上升，阻碍了其广泛应用. 复杂度优化算法(complexity optimization algorithm，COA)牺牲可接受的视频压缩质量以换取明显的编码复杂度下降，是解决上述问题的有效途径，吸引了大量研究人员的兴趣.

目前，针对平面视频编码的COA研究相对成熟，可作为全景视频COA的重要参考，该类算法根据复杂度是否可变分为固定COA和自适应COA. 固定COA采取保守率失真(rate distortion, RD)的策略对编码器进行优化，主要通过实验发现某些编码特性对相应的编码单元进行加速，在几乎不损失RD性能的情况下，降低固定的编码时间. 例如，文[1]利用不同深度编码单元(coding unit，CU)之间的相关性加快了CU模式选择过程，从而降低编码复杂度； Lee等[2]统计了CU的RD代价，进而根据其特性提出了编码模式快速划分算法； 文[3]提出一种基于卷积神经网络以及长短期记忆神经网络的CU划分预测模型，并将其用于降低帧内以及帧间编码复杂度. 固定COA在实用中具有明显的缺陷，即其减少的编码复杂度是固定的，不能适应实际应用场景的需求变化(例如在某些终端计算能力不足的情况下，编码器往往需要更低的编码复杂度). 为克服此缺陷，自适应COA应运而生. 与固定COA不同，它采用灵活RD的策略对编码器进行优化，主要利用编码参数与RD性能的关系对编码器进行整体优化，在不同的RD性能下减少最多的复杂度. 例如，利用帧间各编码层中CU模式候选集与RD性能的依赖强弱，Zhao等[4]在不同的复杂度级别下合理调整各层CU模式候选集，降低RD性能损失. 文[5]基于博弈论在不同的复杂度级别对量化参数(quantization parameter，QP)以及CU划分深度进行调整，从而达到最优的RD性能. Zhang等[6]通过控制编码树单元(coding tree unit，CTU)的深度范围，提出CTU级的自适应COA. 文[7]提出一种基于随机森林的复杂度控制方法，可对编码时间进行精细的控制. 显然，自适应COA比固定COA具备更高的灵活性，在工业应用中更具优越性. 但是，以上自适应COA均针对平面视频场景而设计，未考虑全景视频特性，不能直接应用于全景视频编码.

全景视频与平面视频的最大差别在于视频表现形式，即前者为球面形式而后者为平面形式. 全景视频编码中，需先将其从球面投影至平面，然后再利用平面视频编码框架进行编码[8]. 投影过程使全景视频编码出现与平面视频完全不同的特性. 近年来，随着全景视频的逐步推广，适用于该类视频的COA研究也逐渐引起研究人员的关注，并已取得少量成果. 例如，Wang 等[9]根据球面投影(equirectangular projection，ERP)带来的失真特征提出一种快速帧内预测算法，能在几乎可忽略RD损失的情况下降低24.5%的帧内编码时间. Ray 等[10]根据ERP对全景内容的不均匀采样，提出一种自适应的运动向量以及编码块最小宽度调整算法，在RD性能几乎不变的情况下，可以减少11%的编码时间. Zhang 等[11]首先根据ERP投影的失真特性自适应地调整不同纬度区域的QP，然后根据视频的时空相关性提前终止CU划分，该算法平均可降低42.4%的编码时间. 遗憾的是，由于全景视频是近几年才逐渐兴起的新型视频，当前针对该视频的COA算法均为固定COA，适用范围较窄，性能仍存在提升空间.

为解决上述问题，本研究在深入分析全景视频特性的基础上提出一种帧内复杂度的自适应分配算法，同时结合图像组(group of pictures，GOP)级和帧级复杂度分配实现一个适用于全景视频的自适应COA，最后将该算法实现于目前流行的全景视频编码器平台上，在实用环境中验证所提算法的性能.

1 基于全景视频特性的帧内复杂度分配算法

帧内复杂度分配的目的是将视频帧所得到的复杂度资源分配至各个帧内编码单元，使编码器能够在有限的资源下达到最佳的压缩性能. 首先, 在分析全景视频纬度特性的基础上构建编码复杂度预测模型，实现帧内纬度级的编码复杂度分配； 然后, 构建时间复杂度转换模型，将编码复杂度映射为时间复杂度，以确保编码时间的稳定性； 最后，结合以上两个模型实现全景视频的帧内复杂度分配.

1.1 帧内编码复杂度预测模型

全景视频是一种球形视频，它在编码前需先通过某种投影方式将球形视频转换为平面视频，当前最常见的投影方式是ERP投影. 高效视频编码(high efficiency video coding，HEVC)标准[12]中所提的全景视频ERP投影过程，如图1所示. 编码时将投影后的平面视频根据最大CU宽度分为L个互不重叠的纬度区域，然后使用与平面视频相同的编码技术进行编码.

视频编码中，编码器的计算能力资源被定义为编码复杂度因子(encoding complexity factor，ECF). 如图2所示，编码器通过给各编码层次分配合适的ECF实现复杂度优化[4]，该过程一般分为四个层次，即全局ECF、 GOP级ECF、 帧级ECF以及纬度级ECF，本节研究的是纬度级ECF的分配问题.

图2 复杂度分配总体方案Fig.2 Framework of complexity allocation

在低空间分辨率的平面视频编码中，通常将帧作为最小的复杂度分配单元. 而在全景视频编码中，由于其超高空间分辨率特性以及从球面投影至平面产生的影响，将纬度区域作为最小分配单元也许可以提升编码的整体RD性能. 全景视频经过ERP(如图1所示)投影后，不同纬度的视频内容被不同程度地拉伸，则可能导致帧内纹理产生变化，从而影响CU的模式选择过程. 通过对比平面视频和全景视频的CU数量分布情况来验证全景视频帧内复杂度分配的必要性，其中平面视频考察了BasketballDrive、 BQTerrace、 Cactus、 Kimono、 ParkScene等序列，全景视频考察了AerialCity、 DrivingInCity、 Fengjing_1、 Hangpai_1、 Xinwen_1等序列. 同时，为便于对比, 将CU数量进行归一化处理，结果如图3所示.

图3 平面视频和全景视频的CU数量分布Fig.3 CU number distributions of planar videos and panoramic videos

由于平面视频空间分辨率(1 920 px × 1 080 px)与全景视频空间分辨率(3 328 px ×1 664 px)有差异，所以图3中平面视频有16个采样点，而全景视频有26个采样点. 从图3可以明显看出，平面视频在不同纬度区域的CU分布差异不大，而全景视频不同纬度区域之间的CU分布却具有非常大的差异. 以上分析表明，全景视频不同纬度区域所需复杂度资源具有显著差异，因此对其进行差异化分配比传统的平均分配方式可提升视频压缩性能，即帧内复杂度按下式分配：

θm，n，l=θm，n·wm，n，l

(1)

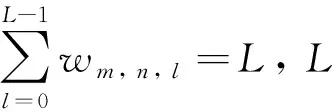
显然，为保证编码质量，wm，n，l不能取固定值，而应随视频内容的变化而变化. 考虑到视频相邻帧之间纹理具有非常高的相似性(相应地也具有非常相似的模式选择结果)，利用相邻已编码帧的CU数量信息预测wm，n，l，从而实现视频内容自适应的帧内纬度级复杂度分配. 预测模型的原理如图4所示.

图4 w(m, n, l)预测模型的原理Fig.4 Prediction method of w(m, n, l)

该模型利用当前GOP中的前n个已编码帧(0～n-1)在纬度上的CU数量分布信息预测当前编码帧各纬度的wm，n，l，即：

(2)

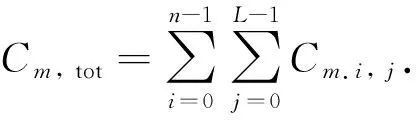
为验证上述预测模型的有效性，通过实验测试其复杂度分配的准确性. 纬度区域的真实CU数量与帧内平均值的比值可反映所需复杂度资源的高低. 该值大于1时，说明该纬度区域需要高复杂度； 小于1时，说明该纬度区域只需要低复杂度. 因此在实验中，当wm，n，l与该比值一致时，被认为分配准确，否则认为分配不准确. 实验使用了5个不同场景下的全景视频，分别测试了在QP=22，27，32，37下的情况，测试结果如表1所示. 从表1可以看出，各个QP的平均预测准确率分别为0.91，0.94，0.95以及0.93，表明本研究所提方法具有较高的分配准确率，可满足实际编码需求.

表1 wm，n，l的预测准确性Tab.1 Predictive accuracy of wm，n，l

1.2 时间复杂度转换模型

编码时间与帧级ECF之间的线性关系对于帧内复杂度分配十分重要. 如果它们之间不呈线性关系，那么用式(1)进行分配会导致帧内编码时间的不稳定. 为此，测试了不同ECF相应的编码时间，并将其归一化(定义该归一化值为时间复杂度因子，time complexity factor，TCF)，结果如图5所示. 从图5可看出，TCF与ECF并不具备良好的线性关系，因此，利用曲线拟合技术获得ECF-TCF转换模型如下：

pTCF=T(θ)=θ1.835

(3)

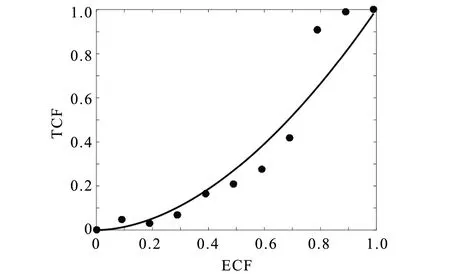
图5 ECF-TCF的拟合结果Fig.5 Fitting results of the relationship between TCF and ECF

在实际编码中，该转换模型将用来确保帧内编码时间的稳定性.

1.3 帧内复杂度分配

综合上述方法可得帧内纬度级的复杂度分配算法，即：当第m个GOP第n帧获得的帧级ECF为θm，n时，首先利用式(3)将θm，n转换为TCF； 然后利用式(1)进行纬度级TCF分配，确保帧内编码时间的稳定性； 最后通过式(3)的逆变换将各纬度级TCF转换为纬度级ECF，以此控制实际的CU模式选择过程. 整体分配方案可描述为：

(4)

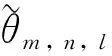
2 总体算法

如前文1.1所述，全景视频编码器的复杂度分配主要分全局、 GOP级、 帧级和纬度级(帧内)等4级，本算法主要研究帧内的复杂度分配，而其它级别的复杂度分配与已有算法[4]类似. 首先，通过参数配置确定全局ECF，即Θ； 然后，针对所有GOP分配相同ECF(各个GOP具有相同编码时间)，即θ1=θ2=…=θM-1=Θ； 接着，利用下式进行帧级ECF分配：

(5)

图6 整体算法流程图Fig.6 Flowchart of the overall algorithm

式中：N代表GOP中的视频帧总数；γn代表第n帧的RD损失对整个GOP的RD性能影响. 利用单纯形法[13]可对式(5)进行求解并获得帧级ECF(即θm，n)； 最后根据式(4)进行帧内复杂度分配. 总体算法的流程图如图6所示.

3 实验结果

为验证所提算法的有效性，在HEVC全景视频编码标准平台(HM 16.16-360lib-5.0)上实现了所提算法，并在全景视频标准测试环境[14]下与全景视频标准编码器进行性能对比. 测试集包含4个8 K视频(Canolafield、 Highway、 Natatorium、 THEPLACE)以及7个4 K视频(DrivingInCountry、 Fengjing_3、 Hangpai_2、 Hangpai_3、 Xinwen2、 Yanchanghui_1、 Yanchanghui_2). 每个视频测试全局复杂度为0.5～0.9(间隔为0.1，即共5个复杂度，模拟实际应用中的不同复杂度需求)的情况，其中各复杂度包含QP为22，27，32，37的情形. 评价指标采用BDBR[15]、 BD-WSPSNR[15-16]和时间节省(time saving，TS). 其中，BDBR用于衡量同等视频质量下，算法对比HEVC标准编码器在码率方面提升的百分比，值越大说明性能越差； BD-WSPSNR用于衡量同等码率情况下，算法对比HEVC标准编码器在WSPSNR(dB)上的提升，值越小说明性能越差； TS则表示算法对比HEVC标准编码器编码时间减少的百分比，体现编码器计算复杂度的减少量. 所提算法8 K视频的实验结果如图7所示.

图7 8 K视频实验结果Fig.7 Experimental results of 8 K videos

从图7可见，本算法可根据预设的全局复杂度将TS控制在25%～60%的较大范围内(全局复杂度越高，则TS越小)，并将BDBR限制在2.7%以下，BD-WSPSNR限制在-0.1 dB以上，这说明在8 K视频编码场景，算法可在压缩性能基本不变的情况下，根据不同的复杂度需求不同程度地降低编码器复杂度. 另外，图7中，BDBR以及BD-WSPSNR随TS增长呈线性增长/减少趋势，这说明在TS较大情况下，压缩性能不易出现突降的情况(而是线性稳定变化)，则用户可根据自身需求对编码器的复杂度进行稳定控制.

所提算法4 K视频的实验结果如图8所示. 该图表明，除了序列Yanchanghui_1以外，利用本算法同样能在基本不影响压缩性能的前提下，根据预设的全局复杂度将TS控制在25%～60%的范围内，这说明本文算法具有较强的适应性. 序列Yanchanghui_1中，本算法在低复杂度(全局ECF为0.5和0.6)场景下带来了相对较高的BDBR损失(虽然TS接近60%)，该性能明显不如其它序列，其原因可能在于该视频中具有大量的快速场景变换，导致所提基于帧间相关性的复杂度预测不够准确. 实际编码中，针对该类视频应设置较高的全局复杂度，以确保视频压缩质量. 另外，综合对比图7和图8可看出，本算法在4 K和8 K视频中的性能差别不大(8 K视频的压缩质量略好，但其TS略差)，表明视频分辨率对算法性能几无影响，算法性能可保持较强的一致性.

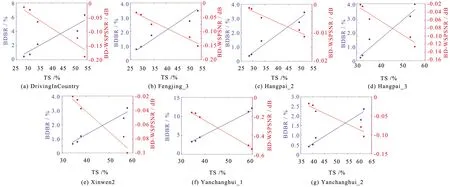
图8 4 K视频实验结果Fig.8 Experimental results of 4 K videos

为进一步验证本算法性能，将文[6]算法实现于相同编码平台，并在相同测试环境中与本算法进行性能对比，结果如图9所示. 从图9可见，随着TS增大，本算法在BDBR上的增长和BD-WSPSNR上的下降均明显慢于文[6]算法. 这意味着在相同复杂度情况下, 本算法的RD损失更小，即本算法对比文[6]算法能在复杂度与压缩性能之间取得更优的平衡. 同时也表明，尽管全景视频与平面视频采用了相同的编码框架，但在全景视频编码中需考虑其从球面映射到平面所产生的投影特性，以提高编码器性能.

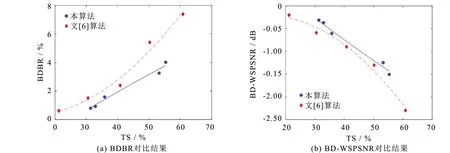
图9 性能对比结果Fig.9 Performance comparison results

4 结语

复杂度优化算法对于视频编码器的实际应用具有重大意义，尤其是自适应复杂度优化算法可以根据实际情况调节编码器以满足需求，是当前视频编码领域的研究热点. 但是，众所周知，目前在全景视频编码领域暂未有自适应COA被提出，而平面视频编码领域的自适应COA直接应用于全景视频性能不佳. 为解决此问题，设计实验深入分析了全景视频的纬度特性，在此基础上提出帧内编码复杂度预测模型和时间复杂度转换模型，进而利用此两个模型实现一种新的适用于全景视频的自适应帧内复杂度优化算法，并最终将该算法实现于当前最新版本的HEVC全景视频编码平台. 实验结果表明，所提算法在不同全景视频场景下均取得良好的性能，具备实用价值.