一种高精度CMOS温度传感器的设计
2020-12-23黄继伟
黄继伟,张 祥
(福州大学物理与信息工程学院,福建 福州 350108)
0 引言
温度传感器作为使用最早、 需求量最大的传感器之一,在许多领域中都有重要而广泛的应用. 近年来,随着无线通信的发展,对精准频率源的要求越来越高. 晶体振荡器作为最常用的频率源芯片,在工作时会因为电流热效应的影响,导致芯片内部温度逐渐升高,输出频率随温度不断变化,性能降低. 为了在不同工作环境中保持良好的频率精度,需要在频率源中引入高精度温度传感器的设计,为频率源中的温度补偿电路提供准确的温度信息.
传统的分立式温度传感器因存在严重的非线性、 自热、 只能输出模拟信号等缺点限制了发展. 与传统的温度传感器相比,片上集成的温度传感器芯片能够输出便于利用的数字信号; 可以直接集成在芯片上,体积更小,更符合传感器微型化的发展方向; 同时片上集成的温度传感器还具有成本低、 测温精度高、 温度分辨率高等优点[1-2].
本研究采用SMIC 55 nm CMOS(complementary metal oxide semiconductor)工艺,设计了一种适用于温补的精密频率源的高精度CMOS温度传感器. 选用SAR ADC(successive approximate register analog-to-digital converter)作为温度传感器的模数转换模块,能够输出数字信号,便于实现频率源芯片的温度补偿.
SAR ADC中引入一种改进的R-2R DAC,省略了运算放大器和反馈电阻,避免了运算放大器失调对量化精度的影响. 而且通过设计一个高阶曲率校正的带隙基准电压源作为R-2R DAC的参考电压,进一步提高了量化精度[3-5].
1 温度传感器的工作原理和结构
1.1 温度传感器结构
温度传感器的框图如图1所示,主要由温度传感电路VPTAT、 带隙基准电路和SAR ADC三部分组成. 其中SAR ADC包括改进的R-2R DAC,动态比较器,SAR逻辑控制电路,非交叠时钟电路.

图1 温度传感器框图Fig.1 Block diagram of the temperature sensor
1.2 温度传感器的原理和误差分析
温度传感器由温度传感电路输出与绝对温度线性相关的模拟量VPTAT,然后SAR ADC进行量化,得到含温度信息的数字信号输出.
由温度传感器的工作原理可知,温度传感器最关键的部分是温度传感电路和模数转换电路. 温度传感电路产生一个与绝对温度正相关的模拟量,产生的模拟量线性度越好,温度传感电路产生的温度误差越小.
已知两个发射极面积不相等的双极型晶体管在相同电流下工作时,基极与发射极构成的电压之间的差值ΔVBE与绝对温度正相关. ΔVBE具有良好的线性度,受工艺的影响较小,所以温度传感电路利用ΔVBE来产生与绝对温度正相关VPTAT[6-9].
模数转换电路需要将输入的模拟信号准确快速地转换为相应的数字信号. 模数转换电路的量化误差直接导致输出误差,引起温度传感器的精度下降. 本设计采用SAR ADC,误差主要分为三部分:一是不可避免的量化误差,由ADC的分辨率和精度决定; 二是采用的R-2R型DAC的实际输出电压与理论电压的误差,受参考电压的电压变化和工艺上不理想引起的匹配误差的影响; 三是SAR ADC在逐次逼近过程中由于时钟抖动造成的量化误差[10-12].
R-2R DAC可以通过增大单位电阻来减小由工艺上的不理想引入的匹配误差. 参考电压引起的量化误差则通过引入高阶曲率校正的带隙基准电路,降低参考电压的电压变化,减小量化误差.
由时钟抖动引起的量化误差,通过引入非交叠时钟的时钟延时,使SAR ADC在工作时避开时钟翻转.
2 温度传感器主要模块的设计
2.1 与温度正相关的VPTAT电路的设计
温度传感电路VPTAT电路图如图2所示. 图中MP1,MP2,MP4支路采用1∶1∶1的cascode电流镜. 电阻R1上的电压降为

图2 VPTAT电路图Fig.2 VPTAT circuit diagram
VR1=VEB1-VEB0=ΔVBE
(1)
流经MP1,MP2,MP4的电流为

(2)
PNP型衬底双极型晶体管基-发射极的关系为:

(3)
2.2 改进型R-2R DAC的设计
R-2R DAC是按比例缩放的DAC,通常是利用电阻阵列把VREF划分为加权电流,然后利用反相运算放大器来产生模拟输出电压VOUT.
采用改进的R-2R DAC如图3所示,省略了运算放大器和反馈电阻,避免了运算放大器失调对量化精度的影响.

图3 改进的R-2R DACFig.3 Improved R-2R DAC

2.3 高阶温度补偿带隙基准源(BGR)的设计
高阶曲率补偿原理图如图4所示. 由于三极管基极与发射极之间的电压VBE不是随温度线性变化,VBE与温度、 工艺相关的等式为

图4 高阶曲率补偿原理图 Fig.4 Schematic of high-order curvature compensation diagram
式中:Vg0为 0 K 时硅的带隙电压;Tr为参考温度;VT为热电压.
VBE的高阶温度特性通过整理可得
VBE(T)=a0-a1T-a2TlnT
(5)
其中:a0是常数项;a1T是线性项;a2TlnT是高阶项. 消去VBE中的线性项仅为一阶线性补偿,为得到更好的温度特性,采用曲率校正技术进行高阶温度补偿.
曲率校正技术是通过产生一个具有正TlnT项的电路,叠加在输出基准上,用来消去VBE(T)中的高阶项TlnT.

(6)

(7)
(8)
流过MP4输出支路上的电流I为
I=I1+I2+I3
(9)
(10)
2.4 SAR ADC
温度传感电路利用ΔVBE输出与温度正相关的模拟电压VPTAT,VPTAT与DAC输出进行比较,当VPTAT>VOUT时,比较器输出1; 当VPTAT 图5 SAR ADC时序图 Fig.5 Timing diagram of SAR ADC 温度仿真是对基准电压进行DC温度扫描,观察电压随温度的变化,从而得出温度系数. 仿真的温度范围是 -20~100 ℃,温度仿真结果如图6. 图6 VREFH,VREFL在各工艺角下温度-电压图Fig.6 VREFH, VREFL temperature-voltage diagram at each process corner 温度系数的计算公式如下: (11) 可得到如表1所述的各工艺角下的温度系数. 表1 VREFH,VREFL在各工艺角下的温度系数Tab.1 VREFH,VREFL temperature coefficient at each process corner 在-20~100 ℃温度范围内,对多个温度点进行模拟仿真,得到如图7所示的温度传感器的精度分析,表明温度传感器仿真环境温度t′与理论温度t的关系. 通过对图7中温度差值的计算,得到如图8所示的温度传感器的误差分析,表明在不同温度t下,仿真温度t′与理论温度t之间的误差Δt. 图7 温度传感器的精度分析Fig.7 Accuracy analysis of temperature sensor 图8 温度传感器的误差分析Fig.8 Error analysis of temperature sensor 对0,0.2,0.4 ℃三个温度点进行仿真,得到如表2所示的温度分辨率的仿真结果. 根据仿真结果可知,温度分辨率在0.2 ℃可以分辨. 电路采用SMIC55nm CMOS工艺完成版图设计,版图如图9所示,版图面积约为(0.55 mm × 0.59 mm). 表2 温度分辨率仿真结果Tab.2 Simulation results of temperature resolution 图9 电路整体版图Fig.9 Overall layout of the circuit 本设计与其他设计的性能比较如表3,可以看出在较低的供电电压,较宽的温度范围下,具有测温精度较高的优点. 表3 与其他设计的性能比较Tab.3 Performance comparison with other designs 基于SMIC 55 nm CMOS工艺,利用Cadence IC615完成仿真与优化,通过采用改进的R-2R DAC和高阶温度补偿带隙基准源的设计来提高SAR ADC的量化精度,实现了一种高精度温度传感器的设计. 仿真结果表明,在1.2 V电源电压、 820 μA动态电流、 -20~100 ℃温度范围条件下,传感器温度精度为+0.32 ℃,温度分辨率为0.2 ℃.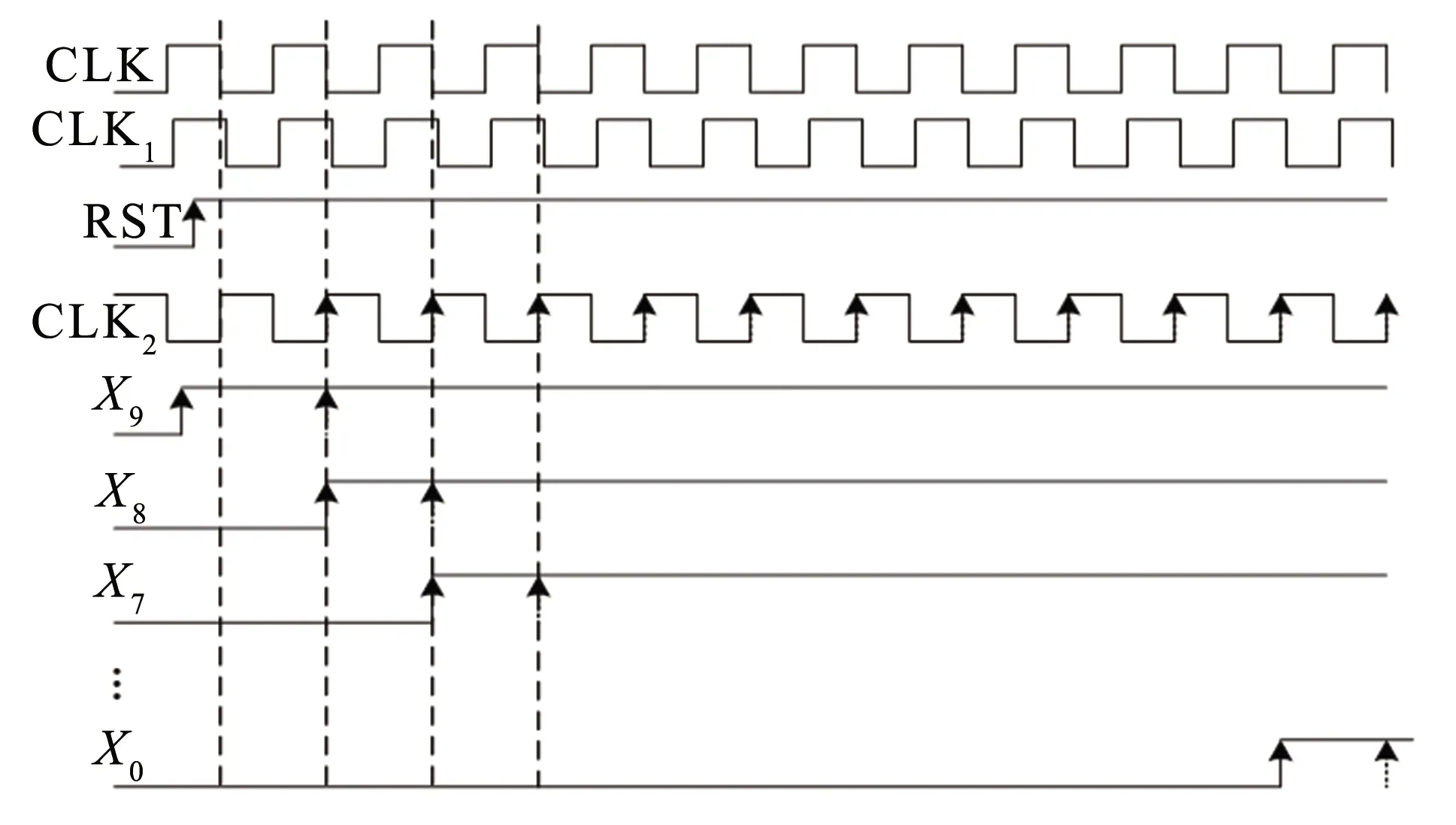
3 电路仿真与数据分析
3.1 温度仿真



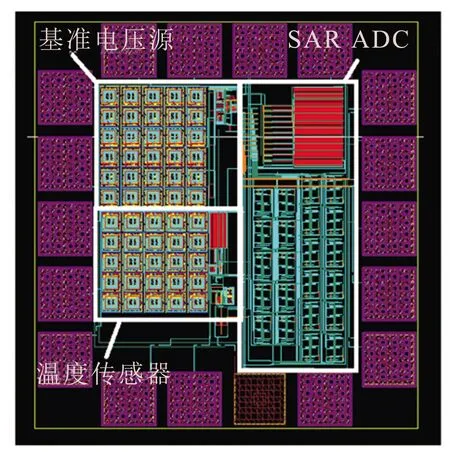
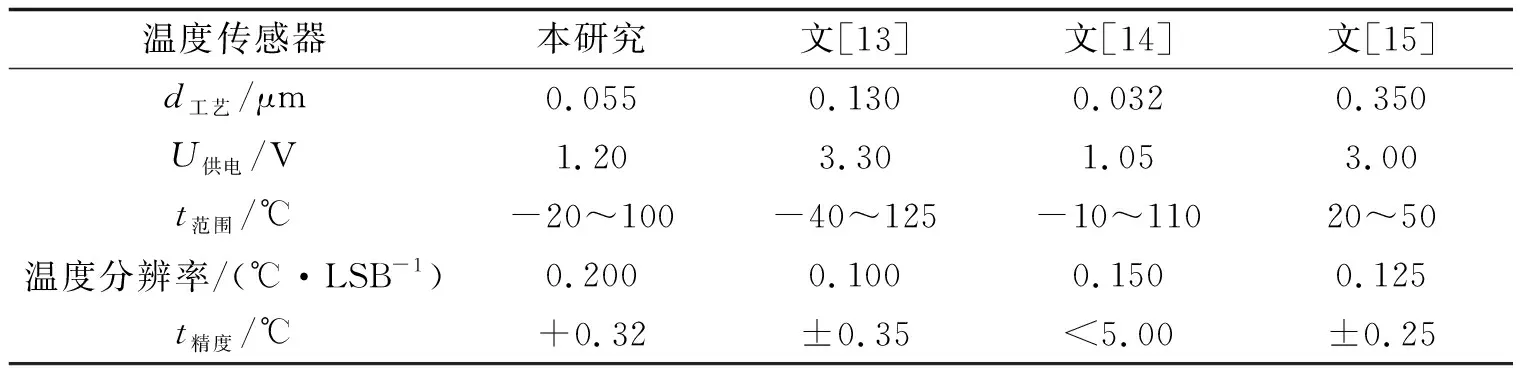
3.2 整体电路后仿结果



4 结语
