积分方程法在载体磁场补偿中的应用∗

嵇绍康 高艳丽

（海军航空大学青岛校区 青岛 266041）

1 引言

利用地磁场进行导航是近几年研究热点［1～3］，具体有以下几个优点［4］：1）可以完全自主且根据外部变化实时进行修正，抗干扰性和隐蔽性较好；2）与其它导航方式进行组合导航也表现较出色（与惯导组合使用，校正导航过程中的积累误差）；3）可实现载体在地貌特征极少的地区运行；4）有实现变轨制导的可能性，提升导弹的突防性能。

地磁导航在工作过程中需要实时获取精度较高的地磁场信息［5～6］，但是，由于载体自身存在恒磁磁场以及载体中软磁材料被外磁场磁化所产生的磁场会严重干扰载体上所安装得测量地磁场信息的传感器［7］，如何避免“杂质”磁场的影响，获取精准地磁场信息是目前地磁导航需要解决的一个难题。

近年来，许多学者、机构对地磁导航如何进行补偿开展了许多的研究与实验，同时提出了多种补偿方案［8～13］，其中在数据拟合和补偿过程中将载体运动范围拓展到三维空间进行补偿的研究相对较少，且存在一定的局限性。

本文基于积分方程法理论［14］，建立了地磁场误差补偿模型，明确了模型中各类参数的物理意义，通过参数求解得到恒磁磁场及激磁磁场系数，解决了磁场干扰补偿的问题，实验室测量结果较理想。

2 积分方程法

应用积分方程法理论，铁磁物质受地磁场磁化在P点产生的场强为。

如图1所示。

图1 磁场源区示意图

铁磁区a受磁化而产生的磁场强度表示成：

铁磁区为飞行器壳体即内部各铁磁物体所占的区域，将其分为n 个单元，并设各个单元的磁化率分别为x1、x2、x3、x4…xn。首先我们在这里假设各单元内的磁场强度为同一值，则对于三维场的第j个单元，有：

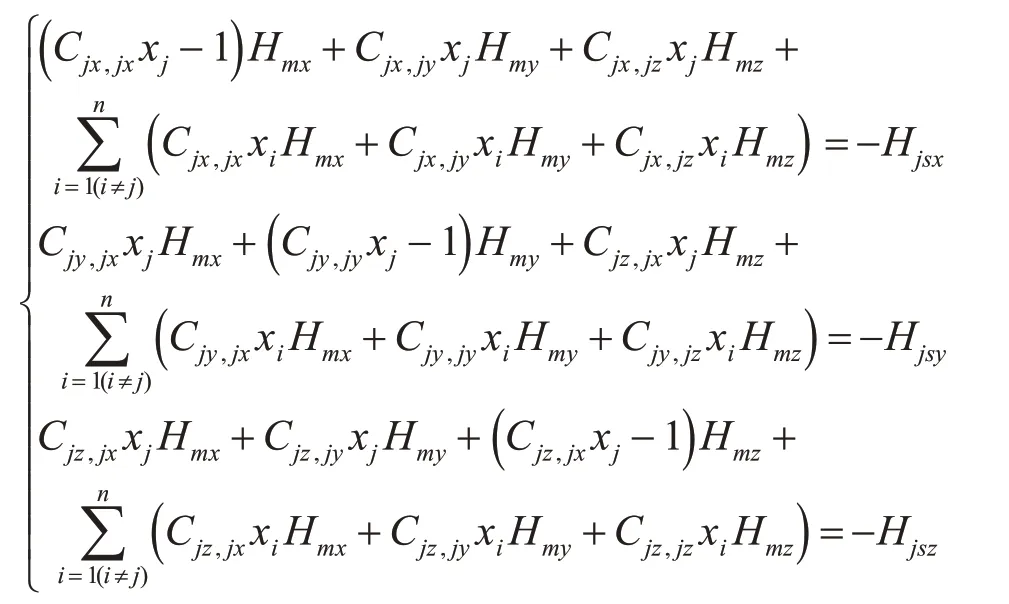
解此方程组即可求出场点a 处的磁场强度与磁化源间的关系：

由于式（4）中左边的系数矩阵包含的干扰补偿系数都是常数固定值，所以我们可以将其简化为

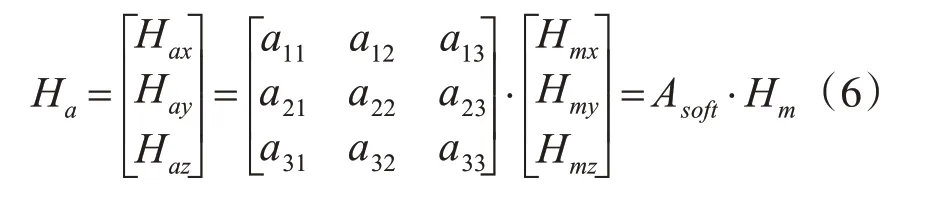
这里的Hm即载体上地磁场场强。

3 误差模型分析

三轴磁传感器测量值可表示为

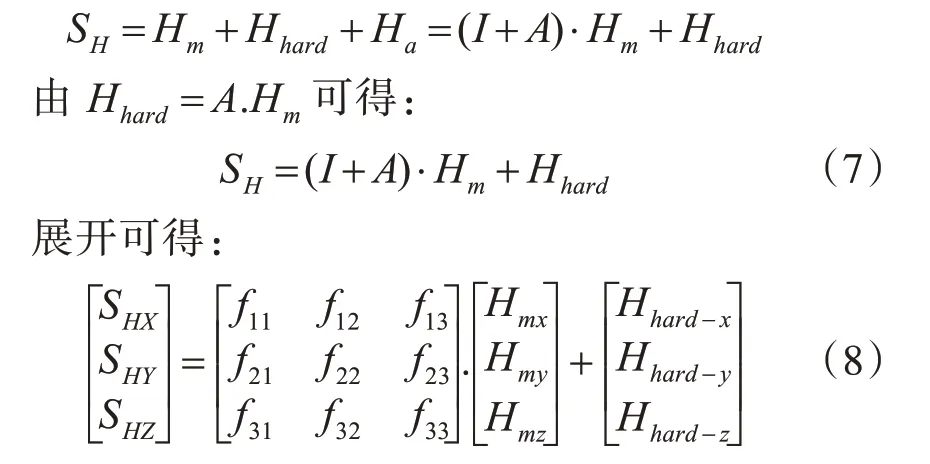
公式中包含3 个恒磁磁场固有参数和系数矩阵中的9个常系数f11、f12、f13、f21、f22、f23、f31、f32、f33，因此实验室环境下需要至少测得四种姿态下地磁场三分量，才可解得12个补偿系数值。

式（8）中含有待求误差模型参数，可变形为

式子中含有12 个待求误差模型参数，测量四种姿态下的磁场数据。将四种姿态下的数据合并就可采用最小二乘算法［15］求得误差补偿参数。

4 补偿算法仿真分析

为了验证该补偿算法的有效性，我们在实验室环境下，利用实验器材无磁三轴转台、FVM-400 三轴磁通门磁力仪和体积为0.003 m3的矩形铁块进行测量试验。首先调整转台三轴方位归0，将磁力仪安装于三轴转台工作台面中心位置，记录下转台不安装铁块时8 种不同姿态的地磁场三分量，以此作为地磁背景场值，同时记录下此时的转台姿态。然后，安装上铁块作为地磁测量干扰源，调整三轴转台处于上述8 种对应姿态，分别记录载体在不同姿态下磁力仪的三轴分量，将上述8 组实验数据分别列于表1。

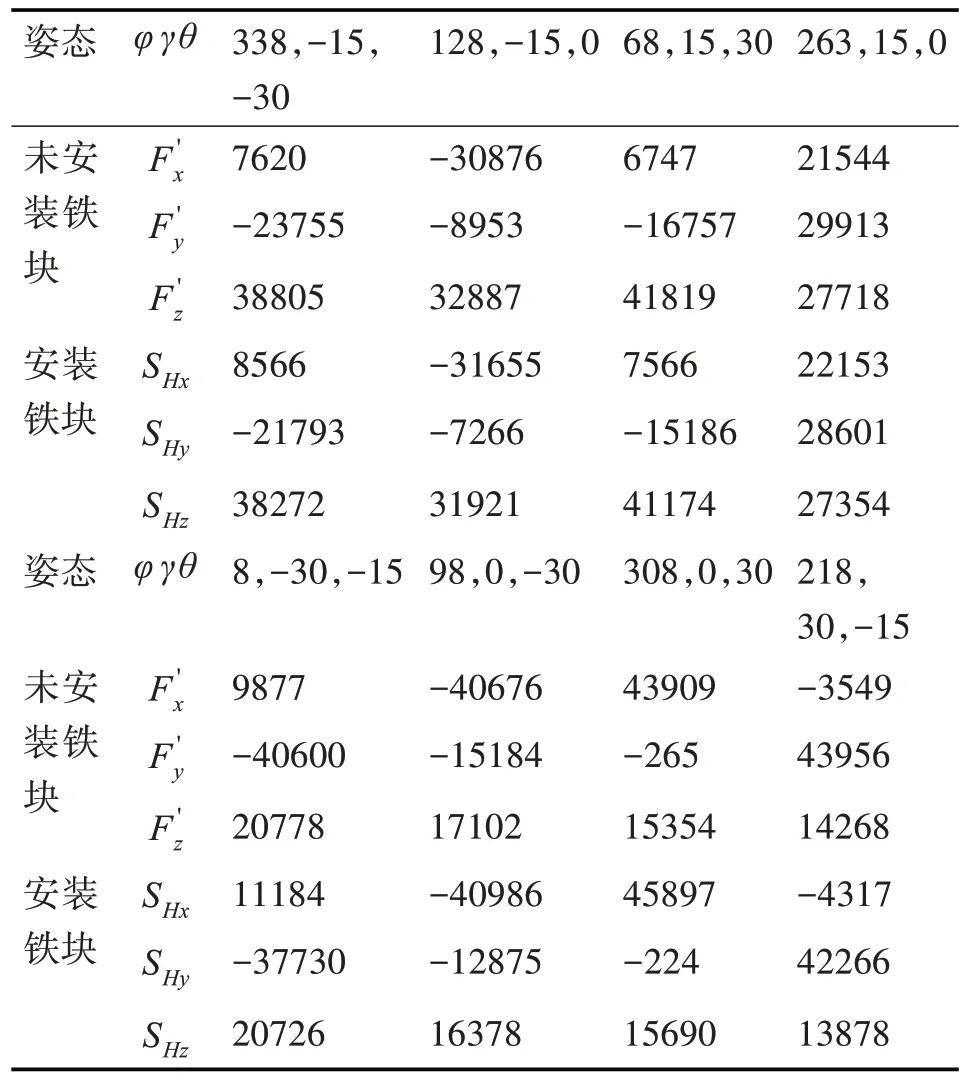
表1 实验数据

将上述实验数据通过Matlab进行仿真编程，计算得到式（8）中的12 补偿系数，然后使转台处于表2 的5 种姿态下，分别测量安装铁块和未安装铁块时各种姿态下磁场三分量，计算5 种姿态补偿后的磁场三分量。将补偿前后实验数据与实际地磁场大小作比较如表2 所示，从表中可以看出补偿后的磁场测量值误差大大降低，达到了预期的效果。

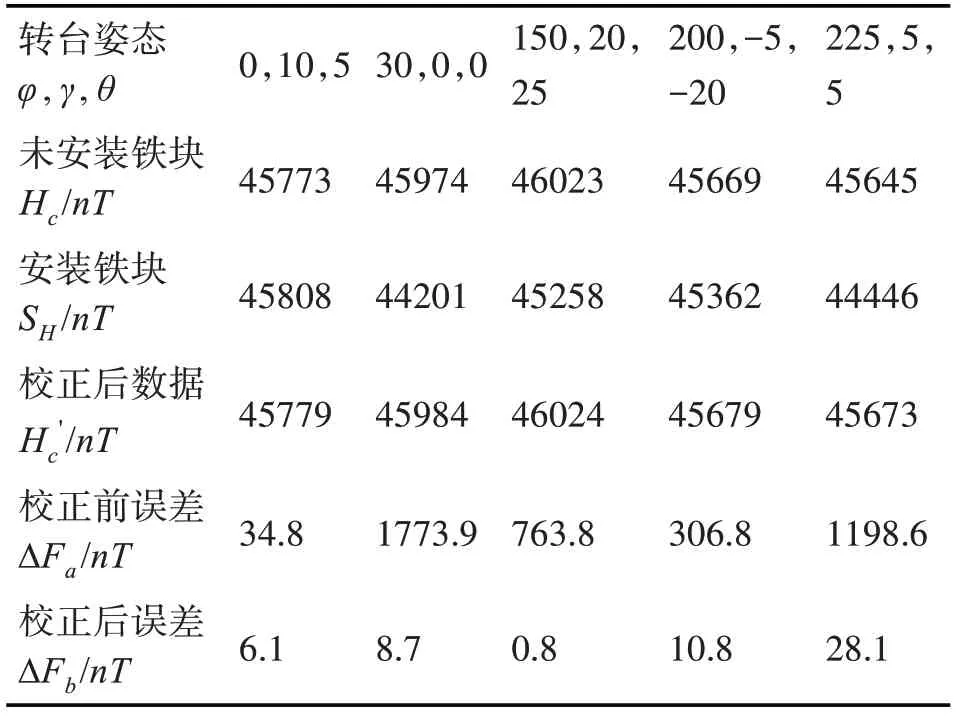
表2 误差比较

5 结语

本文对载体自身磁场特性进行了分析了解，并着重对感应磁场的产生机理做了详细研究，建立了地磁导航干扰误差补偿综合模型。明确了模型中各参数的物理意义。最后运用简单的系统辨识最小二乘估计算法求取误差特性参数。实验数据表明，该技术简单易运算，较好地满足了实际的需要。