双站测向阵列中点的目标到达角近似求解

郁 涛

(上海裕韬智能科技有限公司,上海201802)

0 引言

已有的研究结果表明,如果将程差方程和几何辅助关系结合起来,就能得到平面双基三站定位方程的线性解,由此即可得到适用于长基线的双基三站程差测向公式。在此基础上,通过适当的简化处理,即可获得长短基线都适用的单基中点测向解[1]。为进一步提高单基中点测向解的准确度,文献[1]采用将程差的几何投影式展开,并将站点处的到达角转换为基线中点的到达角的方法,给出了一个基线中点目标到达角的严格解。这个严格解以站点处的到达角与增量角之和来表示单基中点方位角,但实际上其中的增量角是未知的。这个严格解最终仅在近似简化消去增量角之后,给出了一个利用双站交会角使计算准确度更高的近似解。

现有的单基中点测向解的解析分析是建立在程差测量的基础之上的,和这种程差测量直接对应,基于双站时差测量的高精度长基线测向或定位问题[2-3]已经被研究。双站无源定位仍是一个极具发展潜力的研究课题[4]。作为整个拓展应用研究过程的一个过渡阶段,本文从定位三角形的边角关系入手,通过程差与角度之间的转换,研究了基于双站角度测量的阵列中点方位角的计算问题。主要目的是期望得到一个既简单,又有较高计算准确度的解析计算式,以利于进一步的研究分析。

1 定位三角形的边角关系

图1为单基定位三角形的示意图。其中,T为被探测目标,S1和S2表示探测站点,d为站点间基线长度,r1和r2分别为对应站点的目标径向距离,α1和α2分别为两站点处以站间基线为测量基准的目标方位角。

根据图1中定位关系,由正弦定理可得到

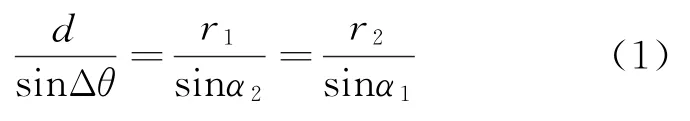
式中:Δθ=180°-α1-α2为目标处的交会角。

由式(1)可得到两站点到目标的径向距离

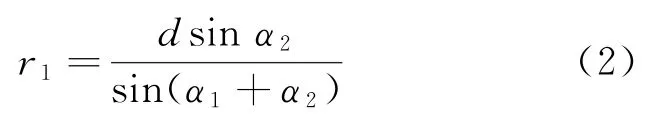
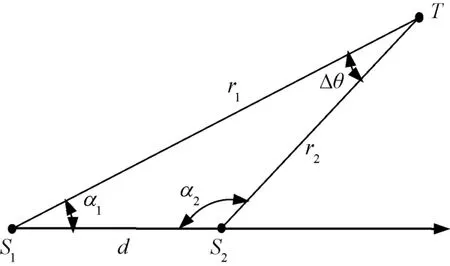
图1 单基定位三角形

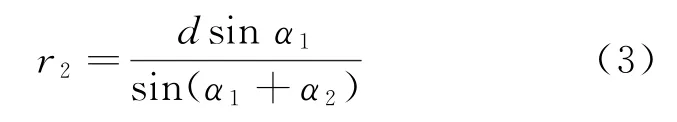
如将两径向距离相减,则可得到站点S1和站点S2间的程差Δr1]2与方位角之间的关系式

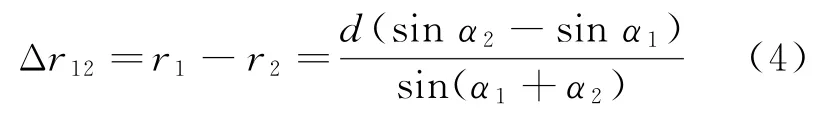
图2为一维双基定位三角形的示意图。站点S2位于站点S1、站点S3连线中点,d为站点S2与站点S1、站点S3]间基线长度,r1、r2、r3]分别为对应站点的目标径向距离,α1、α2、α3]分别为对应站点处以站间基线为测量基准的方位角,θ2为站点S2的目标到达角。可以分别得到相邻两个站点间程差和方位角的关系式。其中,Δ r1]2与方位角关系见式(4),Δ r2]3与方位角关系式为

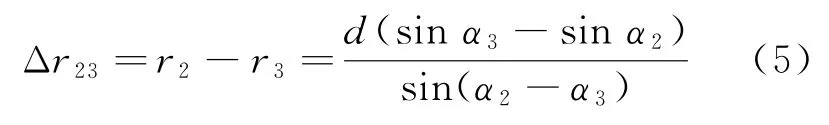
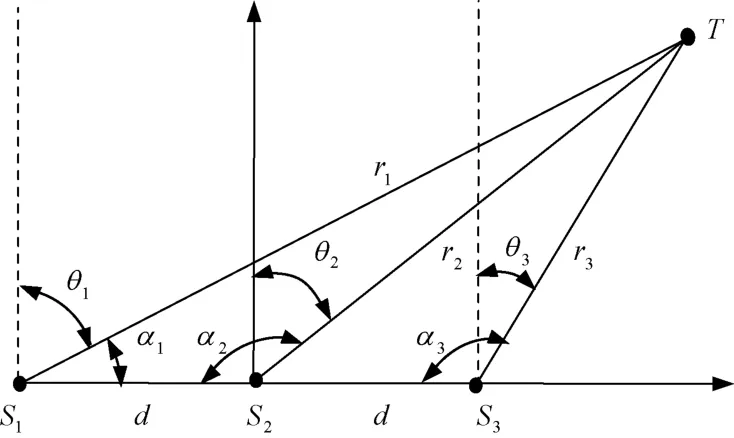
图2 一维双基定位三角形

对于整个双基定位三角形,利用上述的方法,可得到站点S1和站点S3间程差Δ r1]3和方位角之间的关系式

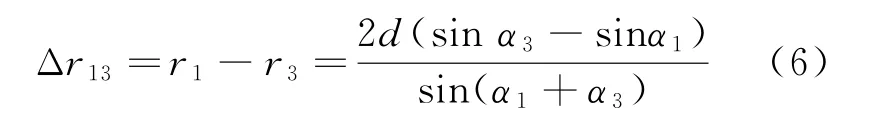
2 从程差到角度的变换

2.1 基于程差测量的近似测向公式

通过直接对一维双基测向公式[1]中程差的高阶项做近似处理,可得到仅与程差测量相关的目标到达角θ2的单基近似测向解[2]

借助几何投影的方法,将基线投影到程差所在的径向方向上,可得到一个能利用双站间的交会角有效提高计算准确性的单基修正近似测向解

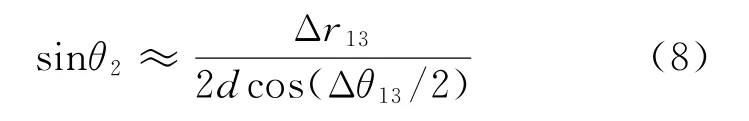
式中:Δθ1]3=180°-α1-α3,是站点S1和站点S3之间的交会角。

2.2 近似的几何解释

如图3所示,对于双站定位系统,由目标和两个观测站所构成的定位三角形△S1TS2可被分解为两个三角形:一个是和程差相关的,称之为程差三角形△S1BS2;另一个是扣减程差三角形后所得到的等腰三角形△BTS2。

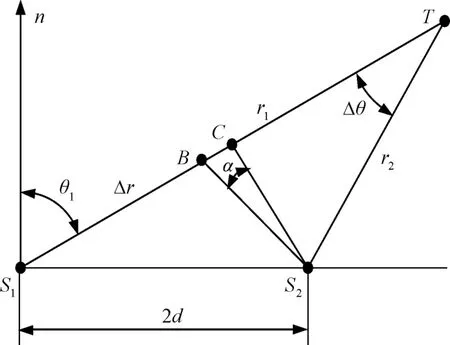
图3 定位三角形的分解

对于等腰三角形△BTS2,根据两底角相等的条件,可得

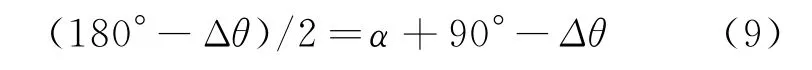
式中:α=∠BS2C为修正角。

由此即可证得

根据图3所示的几何关系可得

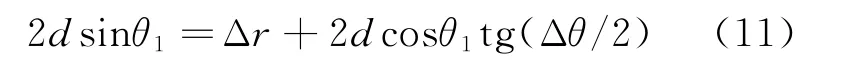
如忽略实测程差所在直角边的修正长度Δa=2dcosθ1tg(Δθ/2),则即得到近似测向解。

2.3 边角关系的演绎

将式(6)代入式(7),可直接给出利用阵列两端点测向值的单基中点测向解

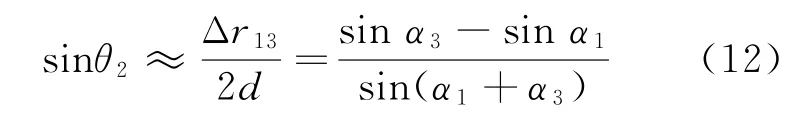
利用三角函数的倍角关系以及和差化积关系,可将式(12)变形为

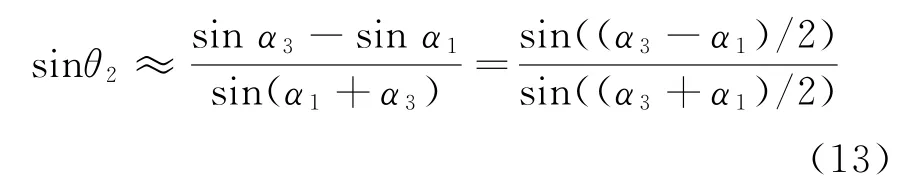
从图2可知方位角与到达角之间的关系为α1=90°-θ1和α3=90°+θ3,代入式(13),有

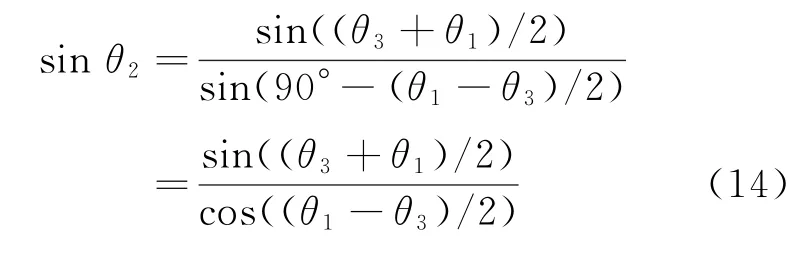
对于远距目标,θ1-θ3将是一个很小的量,此时cos((θ1-θ3)/2)近似为1,于是近似有到达角之间的中值关系为

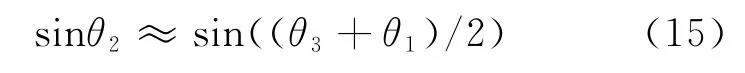
因此,在双站阵列中点的目标到达角可以直接用阵列端点处的到达角进行近似估计。

3 基于程差关系的双站测算解

对于图2所示一维双基阵列,程差之间关系式为

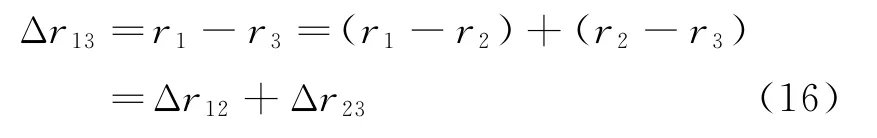
根据式(4)～式(6),将基于角度测量的程差表达式代入式(16),得到

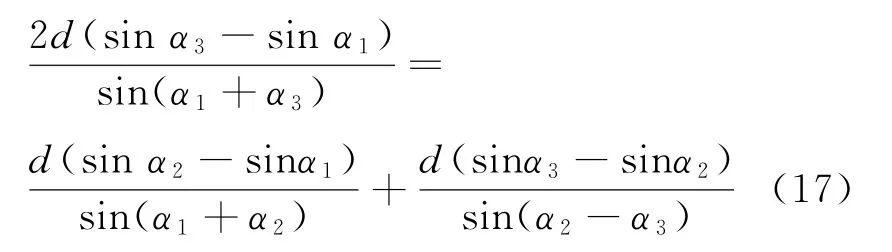
将阵列中点的方位角α2作为未知量求解,且为形式简单,上述方程的左端直接用Δ r1]3表示。可解得方程

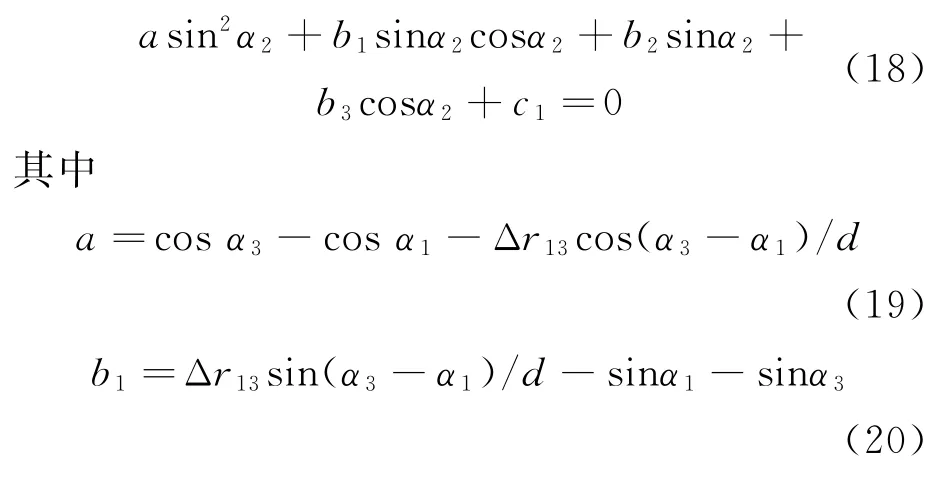
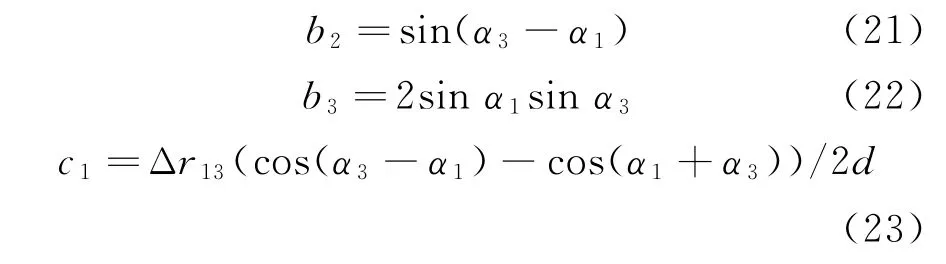
在此基础上,如进一步做函数变换,例如将余弦函数化为正弦函数,则将出现一元四次方程,即使给出显示解亦难以应用于工程解析分析。为此采用近似,先将式(18)中的余弦函数变换为

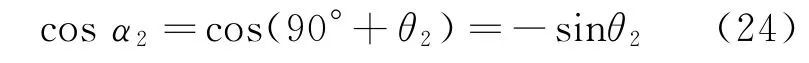
将式(8)代入式(24),得到

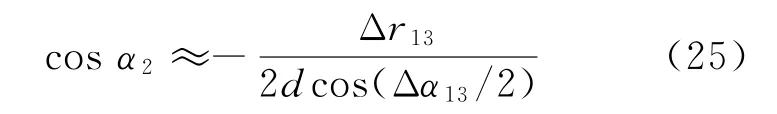
于是,求解方程式(12),可表示为

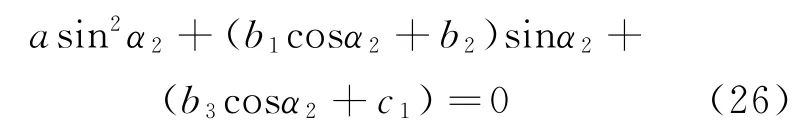
进一步的简洁表示为

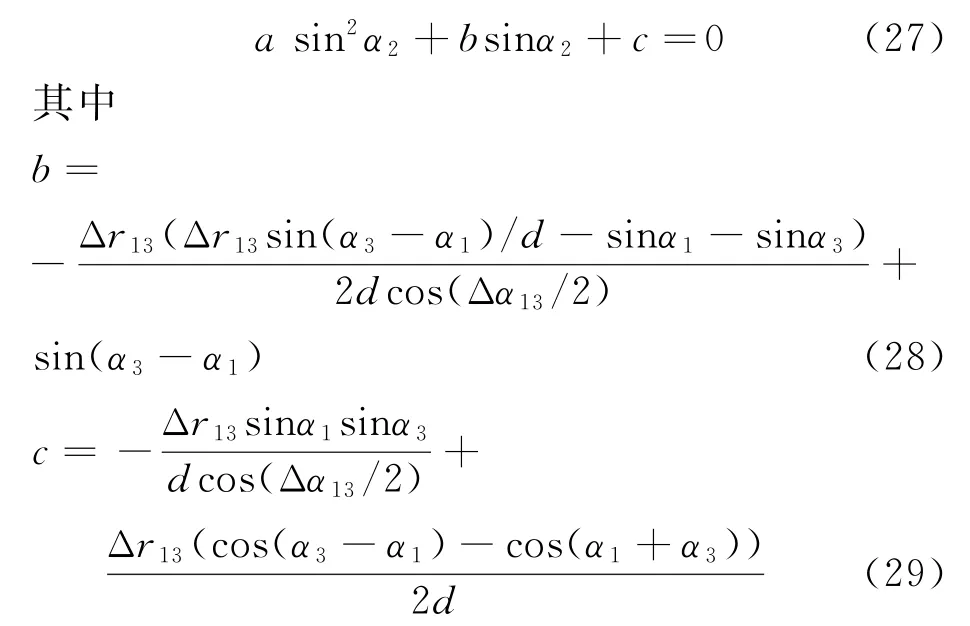
经计算验证,基于程差关系的双站测算解公式为

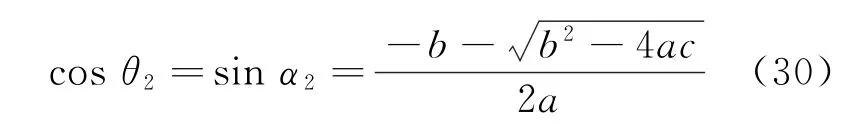
4 计算准确度分析

4.1 相对计算误差理论参考值

从理论角度,为确定计算准确度,可使用文献[1]给出的双基测向解作为基于双站测向角测算阵列中点目标到达角的理论参考值。计算公式为

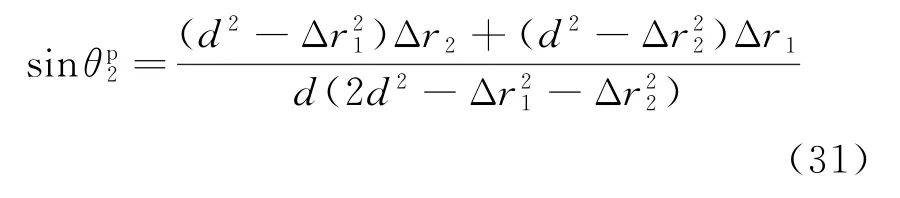
式中:上标p表示是理论值。相对计算误差为

但实际模拟计算时,为处理简单,是先直接设置中点到达角、中点径向距离和基线长度,并让预设的阵列中点到达角在指定区间内线性变化,然后用预设值计算出定位三角形内的各个几何参量,由此就可按式(30)给出阵列中点目标到达角的计算值。

图4给出了当目标距离为300km时,不同基线长度情况下的相对计算误差理论值。计算结果表明,对于300km远的目标距离,只要站间距离小于200km,则基于双站测向角测算阵列中点目标到达角的相对计算误差就能小于1.5%。如果站间距离大于200km,则双站测算解将不再有效。

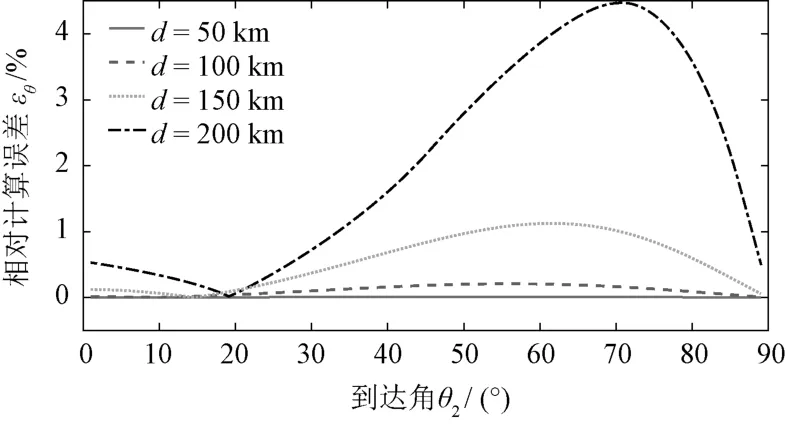
图4 不同基线长度的相对计算误差

4.2 解算准确度比较

图5给出了双站测算解和修正近似解的相对计算误差。计算的参数为:基线长度d=100 km,目标距离r2=300km。由图示曲线可见,双站测算解的计算准确度略高于修正近似解。

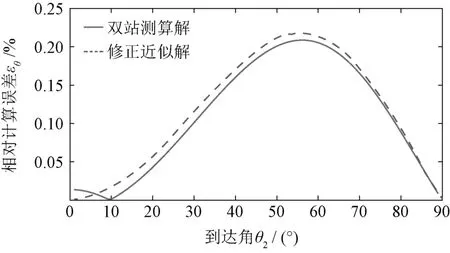
图5 计算准确度的比较

5 结束语

基于角度测量的数学处理过程较为繁杂。基于双站角度测量,利用相邻两基线的程差和关系,所得到的单基中点测向的严格解析解涉及一元四次方程,直接求解高阶方程所得到的严格解析解并不适合工程解析分析。本文的分析仅是初步确定,利用双站交会角改进单基中点修正近似测向解的计算准确度和双站测算解的计算准确度基本相同,换句话说就是用修正近似解即可取代高阶近似的解析解。