机器学习中随机递归梯度算法的步长规则
2020-12-21王福胜
甄 娜,王福胜
(太原师范学院 数学系,山西 晋中 030619)
0 引言
在大规模机器学习背景下,广泛考虑下列优化问题:
(1)
其中n是训练集大小,每个fi,i∈{1,2,…,n}是凸函数且有Lipschitz连续导数.这类问题在监督学习应用中经常出现,而在应用中通常n相对比较大使得标准的梯度下降(GD)方法效率较低,因为它需要多次计算全梯度.针对这个不足,随机梯度下降(SGD)[1]进行了改进,它在每次迭代中随机选取训练集中的一个实例来近似全梯度.在SGD的第t次迭代中,更新规则为:
xt+1=xt-ηtfit(xt),
(2)
其中下标it可以从{1,2,…,n}中随机选取,ηt>0在机器学习中通常被称为学习率,即优化迭代中的步长.在(2)中通常假设随机梯度估计fit(xt)的期望值是F(xt)的无偏估计,即Ε[fit(xt)|xt]=F(xt).然而随机选取一个实例将可能产生方差,不能确保目标函数F(xt)收敛.为了克服这个缺陷,人们通常在迭代过程中选取一个下降步长序列以更新步长,一般情况下SGD的下降步长ηt满足如下条件:

(3)
但这种做法又会导致随机梯度方法的收敛速度较慢,在强凸条件下,标准的SGD算法是次线性收敛的.
近年来,有关学者通过引入方差约简技术进一步改进了SGD算法,例如随机双坐标上升(SDCA)[2],随机方差约简梯度(SVRG)[3],小批量半随机梯度下降(mS2GD)[4],随机递归梯度(SARAH)[5]等.值得注意的是,上述大部分算法均使用固定的步长.文献AdaGrad[6]基于过去梯度的平方和自适应地选择步长,获得了较好的数值效果.在非线性优化问题的算法设计中,BB步长方法[7]具有较好的特性,戴彧虹等学者对此进行了深入研究,获得了丰富的成果[8-11].近年来有关学者创新性地将BB方法与梯度下降方法相结合,提出了另外一类算法用于解决机器学习中优化问题,获得了较好的数值效果,例如SVRG-BB[12], SARAH-1-BB[13],STSG[14]等.受上述方法的启发,考虑将交替BB步长方法[8]与随机递归梯度方法(SARAH)结合,提出一个新算法.
1 算法描述
为了构造新算法,首先来回顾一下SARAH算法[5](如算法1所示).实际上,SARAH和SVRG[3]是两种类似的方法,它们执行的是一个通常称为外循环的确定性步骤,即在外循环计算目标函数的全梯度,然后是随机过程.具体来看,SARAH算法的关键步骤是递归更新随机梯度估计:
vt=fit(xt)-fit(xt-1)+vt-1,
(4)
迭代更新规则为:
xt+1=xt-ηkvt.
(5)
相比SVRG的梯度更新:
vt=fit(xt)-fit(x0)+v0,
(6)
根据式(6)发现SVRG的vt是梯度的无偏估计,而SARAH的vt是梯度的有偏估计,但文献[5]中证明SARAH的更新规则的优势在于算法内部循环本身可以实现次线性收敛.
算法1(SARAH)

步2 随机选取it∈{1,2,…,n},计算

令t:=t+1.
步3 若t>m,转步4;否则转步2.
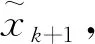

步5 令k:=k+1,若k>epoch,停止;否则转步1.
接下来,介绍一下BB[7]方法.该方法在求解非线性优化问题中取得了良好的效果.考虑下面的无约束优化问题:
minf(x),x∈Rd,
(7)
其中f:Rd→R是一阶连续可导的.文献[7]中给出了标准的BB方法有两种更新步长的规则,即:

(8)
其中sk=xk-xk-1,yk=f(xk)-f(xk-1).当时,有这意味着能够更快地减小目标函数.例如文献[15]讨论了步长规则优于值得注意的是,文献[8]给出两种BB步长的交替使用规则,即:
(9)
其中ε>0是一个常数.注意到式(8)中的BB步长计算不需要任何其它参数,因此考虑将上述的交替BB步长规则与随机递归梯度算法(SARAH)相结合构造一个新的算法,算法框架见算法2.
算法2(SARAH-BB1)


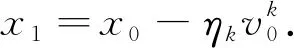
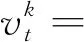
步4 若t>m,转步5;否则转步3.
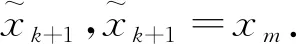
步6 令k:=k+1,若k>epoch,停止;否则转步1.
注:在算法的第2步中ηk等于交替步长规则计算公式(9)除以m,这是因为在内循环中为更新xt,需要将m个梯度估计依次与x0相加.
2 数值实验
在本节中,通过数值实验验证了SARAH-BB1算法的有效性.实验所用数据集如表1,所有数据可以在LIBSVM网站下载.

表1 数据信息
另外,通过解决机器学习中l2正则化逻辑回归问题来比较算法SARAH-BB1、SARAH与SGD,其中正则化参数λ>0,即下列问题:
(10)

在第一个实验中,所有结果如图1所示,包括2个子图(a)和(b),分别对应使用数据ijcnn1,splice.在所有子图中,x轴表示迭代次数k,y轴表示目标损失残差.图1为算法SARAH-BB1中交替BB步长规则的不同参数ε值对目标损失残差的影响,图1中使用了0.1到1范围内的十个值作为参数ε值.为了测试ε值对目标损失残差的影响,对于ijcnn1数据,选择算法SARAH-BB1的初始步长为0.1,对于splice数据,选择初始步长为1.从图1可以看出,当参数ε取值为0.1或0.2时,算法SARAH-BB1的目标损失残差稳定于较小值;因此在下一个实验中,固定ε取值为0.1.值得注意的是,其它ε取值同样可以实现目标损失残差趋于稳定.

图1 不同数据集上算法SARAH-BB1的参数ε对目标损失残差的影响
在第二个实验中,所有结果如图2所示,包括6个子图(a),(b),(c),(d),(e)和(f),其中子图(a),(b)和(c)使用数据ijcnn1,子图(d),(e)和(f)使用数据splice.在所有子图中,x轴表示迭代次数k,y轴表示目标损失残差.图2为算法SARAH-BB1、算法SARAH与算法SGD的目标损失残差对比结果.此外,在图2的子图中,对于算法SARAH-BB1,使用三种不同的初始步长η0,对应红色虚线;而算法SARAH与算法SGD使用三种不同的步长η作为固定步长,其中算法SARAH对应蓝色虚线,算法SGD对应绿色虚线.从图中可以看出,新算法SARAH-BB1的目标损失残差对初始步长η0的选择不敏感,并且经过几次迭代后,它稳定于较小值.值得注意的是,算法SARAH只有选择合适的固定步长时,该算法的目标损失残差才会稳定于较小值.这意味着新的SARAH-BB1算法在初始步长选择上具有鲁棒性.
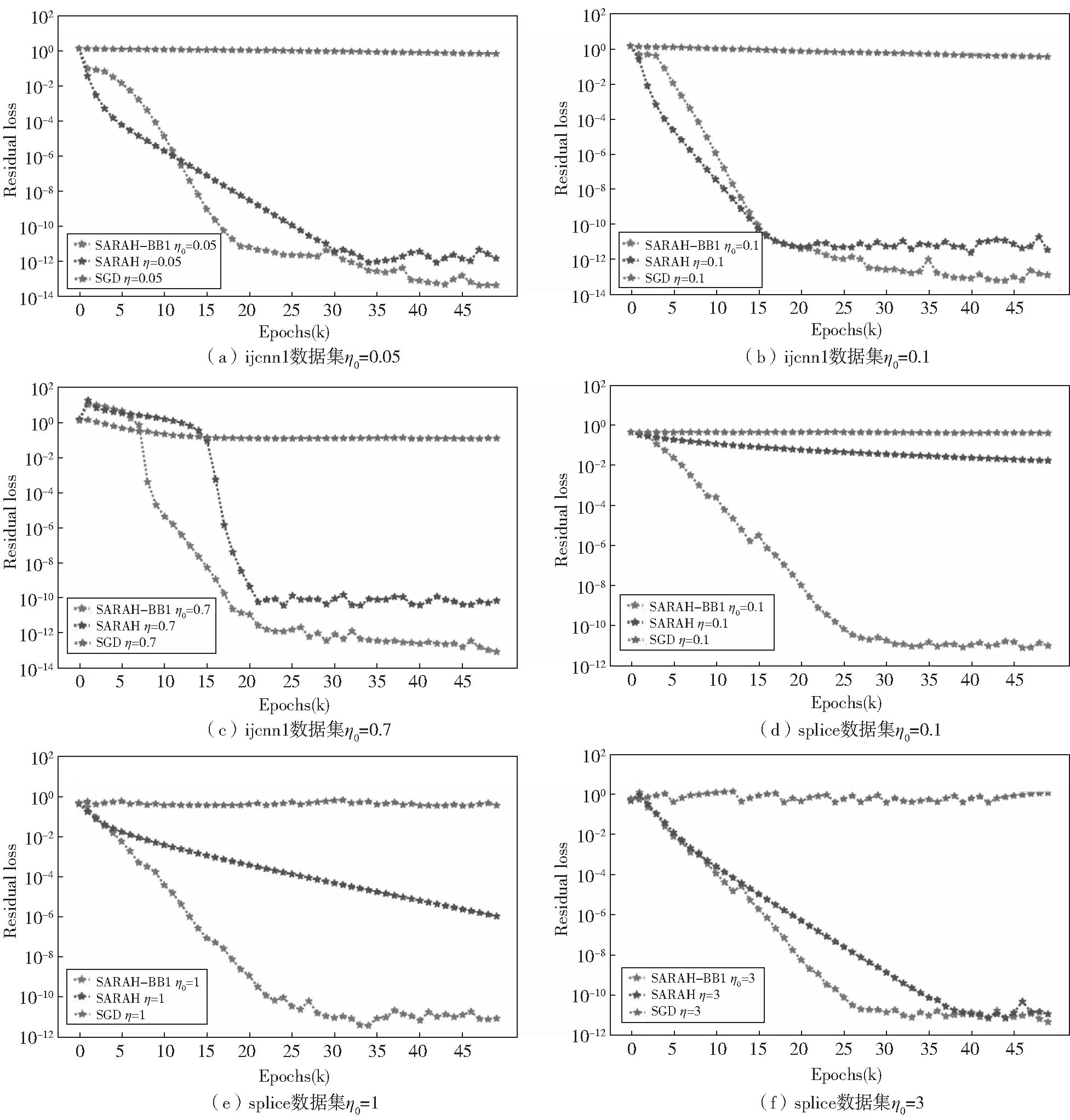
图2 不同数据集上算法SARAH-BB1、SARAH和SGD的目标损失残差比较
3 结论
本文将随机递归梯度算法(SARAH)和交替BB步长方法相结合,提出了一种新的SARAH-BB1算法.新算法在运行过程中可以自适应地调节步长大小,相比已有的使用固定步长的SARAH算法和SGD算法,新算法的收敛速度更快.大量的数值实验表明,本文提出的新算法SARAH-BB1对初始步长具有鲁棒性.
