基于强混样本的带偏差密度模型的小波估计
2020-12-18崔凯利寇俊克
崔凯利, 寇俊克
(桂林电子科技大学 数学与计算科学学院,广西 桂林 541004)
在实际问题中,由于噪声的存在,无法获得真实的测量数据,只能获取含有偏差的数据。考虑基于强混样本的带偏差密度估计模型,即对m∈{1,2,…,M},随机变量Ym,1,Ym,2,…,Ym,nm是同分布且强混的,其密度函数为
(1)
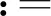
针对上述模型,利用小波方法构造了线性小波估计器,并在积分均方误差意义下讨论该估计器的收敛阶。
1 小波估计器
为了构造小波估计器,首先引入多分辨率分析。
定义1平方可积函数空间L2(R)的一个多分辨率分析(multiresolution analysis,简称MRA)[5-6]是指一列线性闭子空间{Vj}j∈Z满足以下条件:
1)单调性:Vj⊆Vj+1,∀j∈Z;
3)伸缩性:f(y)∈V0⟺f(2jy)∈Vj,∀j∈Z;
4)基的存在性:存在φ∈L2(R),使得{φ(y-k)}k∈Ζ为V0的标准正交基,其中φ为该MRA对应的尺度函数。
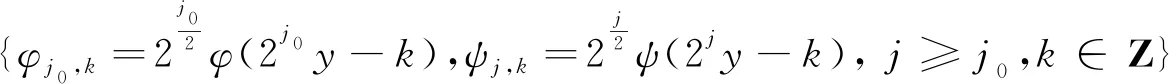
另外,对任意f∈L2(R)且suppf=[0,1],
其中,Λ={k∈Ζ,suppf∩suppφj0,k≠∅},Λj={k∈Ζ,suppf∩suppψj,k≠∅},αj0,k=〈f,φj0,k〉,βj,k=〈f,ψj,k〉。选取Daubechies小波[7]D2 N,其中suppφ=[0,2N-1],suppψ=[-N+1,N]。由于f与φ都具有紧支性,易得集合Λ的基数|Λ|~2j0,集合Λj的基数|Λj|~2j。设AB表示A≤cB,c>0为某一常数,A≻B表示BA,A~B表示AB且BA。
小波作为L2(R)的一组标准正交基,还可以用来刻画Besov空间。
引理1[6]设φ为m(m>s>0)阶正则的尺度函数,且ψ为相应的小波函数,若f∈Lp(R)(1≤p≤∞),则
2){2js‖Pjf-f‖p}j≥0∈lq,
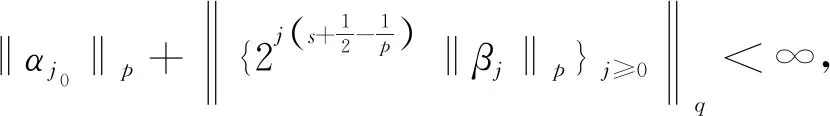
在非参数估计问题中,通常假定
其中常数H>0。
定义2[8]对正整数k,严平稳随机过程{Yi,i∈Z}的k阶强混系数定义为
在构造小波估计器前,还需对模型作以下假设:
H2:存在一个常数c3>0,使得f(y)有正的上界,即0 H3:对任意k∈Z,强混系数满足α(k)≤γe-c|k|θ,其中γ>0,c>0,θ>0。 H4:对任意m∈{1,2,…,M}及i∈{1,2,…,nm},设(Ym,1,Ym,i+1)的密度函数为g(Ym,1,Ym,i+1),则存在c4>0,使得 |g(Ym,1,Ym,i+1)(y,y′)-g(y)g(y′)|≤c4。 H1在带偏差密度估计模型中是必不可少的[1-4],H3、H4可以看作是对随机变量强混的不同表述[9-10]。 线性小波估计器 (2) 其中: (3) (4) 引理2针对密度估计模型(1), 仿真中A相励磁涌流第1个波峰峰值为231 A,实测中A相励磁涌流第1个波峰峰值为218 A,仿真相对实测误差仅为6%。此外,两者波形变化趋势保持高度一致,充分证明了基于电压积分法的剩磁评估方法和PSCAD变压器饱和模型的可用性,以及所提剩磁施加方法的正确性,为变压器合闸励磁涌流评估以及主变压器消磁效果评价提供了一种手段。 证明由于Ym,1,Ym,2,…,Ym,nm同分布, 根据式(1)可得 类似地, 引理3假设模型(1)满足H1~H4,且2j≤nm,则 (5) (6) 证明对于式(5),由方差的性质可得 (7) 依据式(1)和H1、H2, (8) 因为Ym,1,Ym,2,…,Ym,nm是严平稳,且2j≤nm,则不等式(7)的第2项可转化为 首先估计T1。由H1、H4可得 |∬(y,y′)∈[0,1]2(g(Ym,1,Ym,l+1)(y,y′)-g(y)g(y′))· ∬(y,y′)∈[0,1]2|g(Ym,1,Ym,l+1)(y,y′)-g(y)g(y′)|· 因此, (9) 估计T2。利用Davydov不等式(p=q=4)以及H1,则 进而, (10) 联合式(9)、(10),不等式(7)右端第2项的上界为 再结合式(7)和(8)可得 对于式(6),依据式(7)和H1可得 (11) 利用Davydov不等式(p=q=4)和H1可得 证明由三角不等式知, (12) (13) (14) 联合式(13)和(14)可得 (15) 因此,对于1≤p<∞,式(15)恒成立。 (16) 另外,利用凹函数的性质可知, (17) 利用引理2和引理3可知, (18) 即 联合式(16)和(17)可得2 2个引理
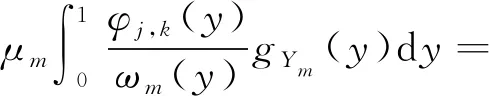
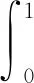
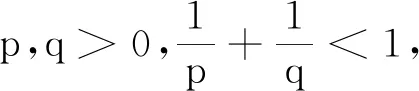
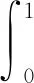
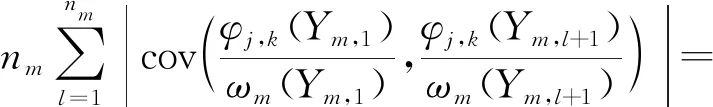
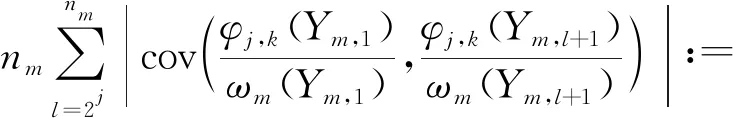
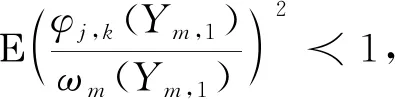
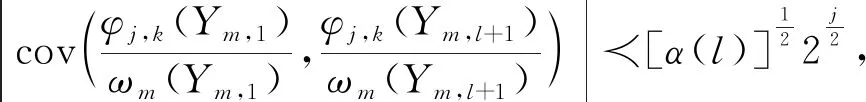
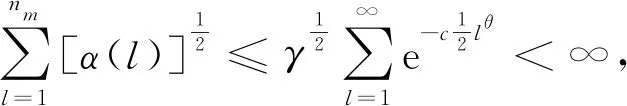
3 定理
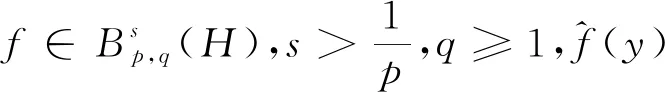
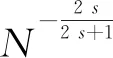
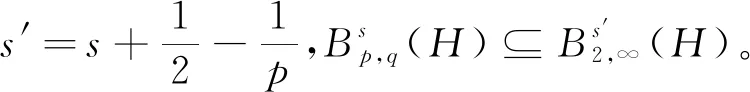
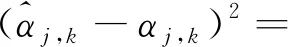
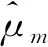
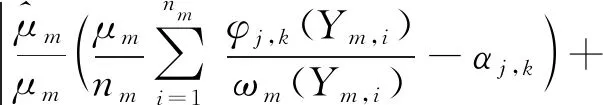
4 结束语
