基于辅助粒子滤波波动率估计算法

陈 影， 蔡如华， 杨 标， 吴孙勇

(桂林电子科技大学 数学与计算科学学院，广西 桂林 541004)

金融资产收益波动性的准确估计对投资组合管理、风险管理和期权定价具有重要意义。到目前为止，人们已经清楚地认识到，波动既是时变的，在一定程度上也是可预测的。近年来，金融资产收益波动性估计的重要性和广泛应用使得波动率建模成为金融时间序列分析中一个非常活跃的研究领域。常用的波动率建模方法是随机波动(stochastic volatility，简称SV)模型[1]，但是传统SV模型不适合于波动率迅速变化到一个新水平的情况。这就促使人们对其进行扩展，以利用高频交易价格数据提供的额外波动信息。在高频交易价格数据和已实现测度的背景下，许多学者对SV模型进行了扩展和广泛研究，将已实现测度引入SV模型[2-4]。虽然现有SV模型引入了已实现测度，但是现有的研究较少综合考虑波动率的非对称性与长记忆性。基于此，吴鑫育等[5]综合考虑了波动率的非对称性和长记忆性，构建了双因子非对称已实现随机波动(two-factor asymmetric realized stochastic volatility，简称2FARSV)模型，该模型是SV模型的一个扩展，其在基本SV模型中引入了基于高频数据构建的已实现测度。虽然扩展后的SV模型能够更好地利用高频交易价格数据提供的额外波动信息，但由于高频交易价格数据的非线性及非高斯，使得传统的统计分析方法在此种情况下无法很好地解决金融时间序列的相关问题。

目前，解决非线性非高斯问题的常用方法是粒子滤波[6]。粒子滤波是一种基于贝叶斯理论的估计方法，该方法通过一组采样粒子逼近概率密度函数，并通过加权粒子的平均值得到最小方差的状态估计。标准粒子滤波采用序贯粒子采样，可很好地适应非线性系统。近年来，因粒子滤波在非线性非高斯问题估计中的优势，被广泛应用于金融领域。张高煜等[7]采用粒子滤波技术对波动率进行估计和预测；Djuric等[8]提出了一种利用杠杆模型估计随机波动率的粒子滤波方法。但由于标准粒子滤波采用转移密度作为重要性采样密度，使得抽样粒子在更新之后，似然度较小的粒子大量丢失，重采样后的粒子集中于某几种权重较大的粒子簇上，若一些模型在某些情况下是强非线性的，使得似然峰变化频繁，随着迭代的进行会导致滤波失败[9]。鉴于此，提出了辅助粒子滤波波动率估计(auxiliary particle filter volatility estimation，简称APFVE)算法，相比于标准粒子滤波，辅助粒子滤波利用当前时刻的量测信息，考虑当前时刻量测值的影响，进行二次采样和二次权重计算，修正粒子的分布，使粒子向高似然区域移动，使得更新后的粒子权重更稳定，其状态估计值更接近于真实状态。

1 双因子非对称已实现随机波动(2FARSV)模型

由文献[5]可知，双因子非对称已实现SV模型的形式为：

rt=μ+exp(θt/2)εt,θt=c+h1,t+h2,t,

εt～i.i.d.N(0,1)，t=1,2,…,T;

(1)

(2)

hj,t+1=φjhj,t+τj(εt)+ηj,t,

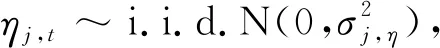
j=1,2,t=1,2,…,T-1；

(3)

(4)

其中：rt为t时刻的资产收益率；xt为t时刻的对数已实现测度；ht为均值调整的对数波动率，服从高斯一阶自回归过程；θt为对数波动率；φ为度量波动率的持续性参数，|φ|<1表示波动率过程是平稳的；εt与ηt相互独立，ut与εt、η1,t和η2,t均相互独立。该模型在2个波动率因子过程式(3)中均引入了非对称效应函数τj(εt),假设其形式为：

τj(εt)=τj,1εt+τj,2(|εt|-E|εt|),

E(τi(εt))=0，

2 粒子滤波波动率估计算法

2.1 标准粒子滤波波动率估计算法

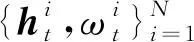
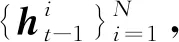
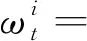
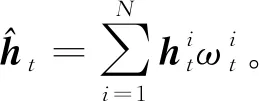
2.2 APFVE算法

虽然粒子滤波易于获取和采样，但是粒子滤波算法只从前一量测和状态采样，未考虑当前时刻的量测值，也未考虑当前框架中可用的粒子，这可能导致大量的低权重粒子丢失，最终导致较高的蒙特卡洛方差以及较差的滤波性能[12]。

辅助粒子滤波[13]以粒子滤波为基础，引入了重要性密度函数q(ht,ik)，其中ik为上一时刻的粒子序列索引。2FARSV模型的APFVE算法实现步骤为：

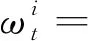
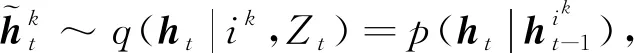
3 仿真实验

利用文献[5]的真实参数值模拟资产收益率，参数向量的真实值为Θ=(0.001,-8.500,-0.500,0.080,0.980,0.030,0.080,0.020,0.400,-0.800,0.040,0.080)，将标准粒子滤波算法和辅助粒子滤波算法分别用于2FARSV模型，对模拟得到的资产收益波动率进行估计。图1为仿真模拟的1 000 d的资产收益时间序列，图2为标准PFVE算法对资产收益进行波动率估计的滤波估计。从图2可看出，资产收益的变化幅度较大，利用标准PFVE算法得到的资产收益波动率变化较为平缓，不能很好地刻画资产收益的变化特征。图3为APFVE算法对资产收益进行波动率估计的滤波估计。从图3可看出，资产收益的变化幅度较大，而波动率的变化趋势较为符合资产收益的变化特征，说明APFVE算法能够更好地捕获资产收益的波动率。从图2、3可知，在资产收益的变化特征方面，与标准PFVE算法相比，APFVE算法的效果更好。

图4为标准PFVE算法与APFVE算法资产收益波动率估计误差，表1为标准PFVE算法与APFVE算法均方根误差(RMSE)和平均绝对误差(MAE)。从图4和表1可看出，无论是资产收益波动率误差还是RMSE、MAE，APFVE算法均比标准粒子滤波算法小，说明APFVE算法估计精度比标准粒子滤波算法精确。

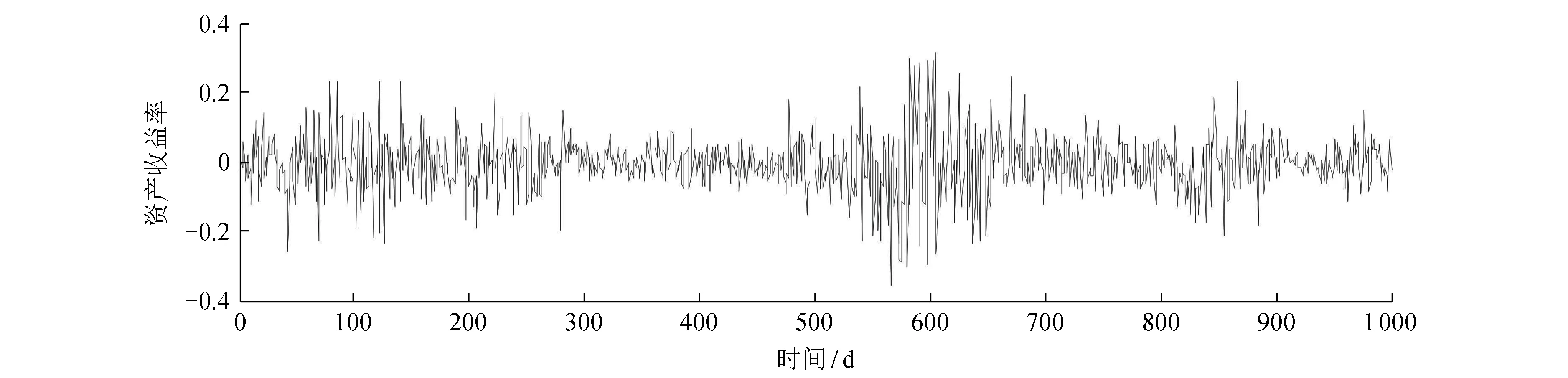
图1 资产收益时间序列

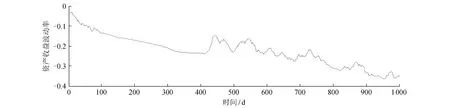
图2 标准PFVE算法资产收益波动率的滤波估计

图3 APFVE算法资产收益波动率的滤波估计

图4 标准PFVE算法与APFVE算法滤波波动率估计误差

表1 标准PFVE算法与APFVE算法的均方根误差和平均绝对误差

4 结束语

针对由于利用转移密度作为重要性采样密度，未采用当前时刻的量测信息，造成了标准粒子滤波对异常值敏感和效率低下等问题，提出了辅助粒子滤波波动率估计算法。辅助粒子滤波利用当前时刻的量测信息对重要性采样密度进行实时调整，并实时修正粒子分布，使得更新后的粒子更稳定。将该算法用于2FARSV模型，仿真实验表明，该算法能够更好地刻画资产收益率的变化特征，更好地对波动率进行估计。