科氏质量流量计中全数字驱动技术
2020-12-18徐浩然徐科军刘陈慈
徐浩然, 徐科军,2, 刘 文, 张 伦, 乐 静, 黄 雅, 刘陈慈
(1. 合肥工业大学 电气与自动化工程学院, 安徽 合肥 230009; 2. 工业自动化安徽省工程技术研究中心, 安徽 合肥 230009)
1 引 言
科氏质量流量计可以直接测量质量流量,具有测量精度高、重复性好等优点,是当前发展最为迅速的流量计之一[1]。科氏质量流量计由质量流量传感器(或称一次仪表)和变送器(或称二次仪表)组成。质量流量传感器由流量管、电磁激振器、速度传感器、温度传感器和外壳组成。变送器由驱动模块和数字处理模块组成。驱动模块为电磁激振器提供信号和能量,使流量管稳幅振动;数字处理模块接收速度传感器的输出信号,交由核心处理器处理,得到质量流量。其中,流量管的稳幅振动是科氏质量流量计工作的前提,所以,驱动部分是科氏质量流量计的重要组成部分。根据驱动信号产生方法的不同,将科氏质量流量计的驱动方式分为3种:模拟驱动、半数字驱动与全数字驱动[2]。模拟驱动依靠模拟电路对驱动信号进行幅值、频率、相位的调节,复杂度低,成本低[3]。在单相流工况下,流量管的固有频率、阻尼比较为稳定,模拟驱动可以取得较好的驱动效果。半数字驱动是模拟驱动向全数字驱动发展的过渡产物,它的频率、相位调节方法与模拟驱动相同,幅值的调节是通过软件调节增益来实现的,驱动能力更强[3]。全数字驱动的驱动信号来自于数字系统的合成,幅值、频率、相位完全受数字系统的控制,驱动能力最强。当遇到气液两相流和批料流等复杂工况,流量管的固有频率和阻尼比将发生很大的变化,数字驱动也能驱动流量管振动[3~7]。全数字驱动技术复杂,实现困难,虽然有多篇论文从不同的方面对全数字驱动技术进行介绍,但是,很少有论文全面地比较全数字驱动中的各项关键技术细节,并针对不同的应用场合,提供对应的技术方案。
本文对科氏质量流量计中的全数字驱动技术进行综述。从驱动技术的控制对象—流量管振动系统出发,研究它在气液两相流下的振动特性,其中,通过使用变送器在线分析流量管振动信号,得到流量管振动频率的波动情况;通过建立流量管振动系统的数学模型,得到流量管阻尼比的变化情况。基于流量管振动系统的振动特性,明确在气液两相流下,流量管振动系统对于驱动技术的要求,再结合不同工况下的测量需求,研究和选择相应的启振方法与驱动参数调节方法,并比较单核DSP实现和双核DSP+FPGA实现方案。
2 流量管振动特性
对驱动技术的控制对象(即流量管振动系统),在不同工况下的振动特性研究,以明确被控对象对驱动技术的要求。
气液两相流下,由于液相的密度与气相的密度不同,流量管横向振动时,液相和气相会发生相对运动,产生摩擦力,该摩擦力最终作用于管壁上,使流量管的阻尼比增大。液相流量较大时,气相与液相混合的较为充分,气相主要以许多小气泡的形式分散在水中;此时,流体中气泡分布的较为均匀,流体通过流量管时的瞬时含气量波动不会过大。液相流量较小时,液相与气相会产生明显的分层;此时,流体中气液两相混合的不均匀,流体通过流量管时的瞬时含气量会产生较大波动。
气液两相流下,流体复杂。流体会对流量管的振动产生直接影响,可采用实验的方法分析该影响。首先,研究流体的波动对流量管振动特性的影响;继而,采用数学建模的方法,研究流量管的阻尼比以及模型中其它参数的变化规律[8]。
2.1 流体的波动对流量管振动特性的影响
分析单相流和气液两相流下,流量管振动频率的波动特性。由于流体状态变化时,流量管的振动频率也会变化,可在不同水流量和不同含气量下,记录流量管振动频率的波动情况。由于不易直接在线测得含气量,为此,引入密度降的概念,通过变送器测得的流量管振动信号频率值,来间接反映含气量[9~11]。密度降Dd的表达式为:
(1)
式中:D0为单相流体的实际密度;D1为混合流体的密度,其计算方法如式(2)所示。
(2)
式中:α1~α4为待标定密度系数;f为流量管振动信号频率;ΔT为流体温度变化值。
流量管的振动表现为流量管振动信号,可记录流量管振动信号反映流量管的振动情况。在水流量为30,60,90 kg/min的情况下,密度降分别为0,0.1,0.2和0.3,用变送器在线计算并保存60 s内流量管振动信号的频率波动情况,具体如表1所示,其中,密度降为0即代表单相流工况。可以看出,单相流下,流量管振动频率波动极小。
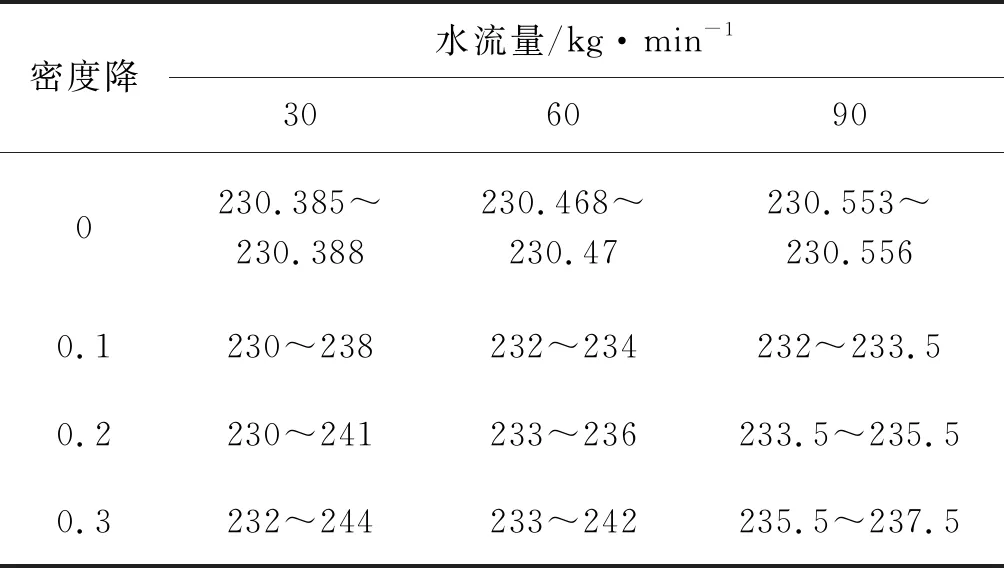
表1 流量管振动频率波动情况Tab.1 Fluctuation of the vibration frequency of the flow tube Hz
气液两相流下,水流量为30 kg/min、密度降为0.1时,流量管的振动频率在230 Hz至238 Hz之间波动,波动范围为8 Hz;密度降为0.2时,流量管的振动频率在230 Hz至241 Hz之间波动,波动范围为11 Hz;密度降为0.3时,流量管的振动频率在232 Hz至244 Hz之间波动,波动范围为12 Hz;水流量为60 kg/min和90 kg/min时,密度降变化时,流量管振动频率波动规律也相同。说明在水流量一定时,密度降越大,流量管的振动频率波动范围越大,即流量管振动的波动性越强。同样,可以看出,同一密度降下,水流量越小,流量管振动情况的波动性越强。流量管振动的波动情况越强,对驱动控制及时性的要求将越高。
2.2 建模分析流量管振动特性
一次仪表工作时,由电磁激振器输入驱动信号使流量管振动,由速度传感器输出流量管振动信号给变送器计算流量。为此,将流量管、电磁激振器和速度传感器定义为流量管振动系统。可通过求取流量管振动系统的数学模型分析流量管的振动特性,以便更好地实现控制[12]。
一般采用二阶数学模型描述流量管振动系统:
(3)
式中:Vi(s)为输入的驱动电压信号;Vo(s)为输出的流量管振动信号;KR为固有增益;ξs为阻尼比;ωn为无阻尼固有频率。
模型中的参数不易直接获取,可采用实验方法获得。具体地讲,给流量管振动系统一个正弦激励信号,然后,测量其输出,根据响应曲线计算模型参数。当正弦激励信号结束时,流量管振动系统的振动就会衰减,并慢慢地停振,此时,速度传感器将输出自由衰减振荡信号,根据此自由衰减信号可计算出阻尼比ξs。对自由衰减振荡信号做基于FFT的频谱分析,得到有阻尼固有频率ωd和无阻尼固有频率ωn。将阻尼比ξs与固有频率ωn代入式(3),令s=jωd,结合正弦波激励信号结束前的稳态驱动电压信号幅值和速度传感器信号幅值即可得到固有增益KR。
同时求取单相流和气液两相流下的流量管振动系统数学模型。具体地,采用上述建模方法分别得到水流量为30,60,90 kg/min,密度降为0,0.03,0.07,0.12,0.2,0.3和0.4情况下的数学模型。结果如表2、表3和表4所示,其中,密度降为0即代表单相流工况。
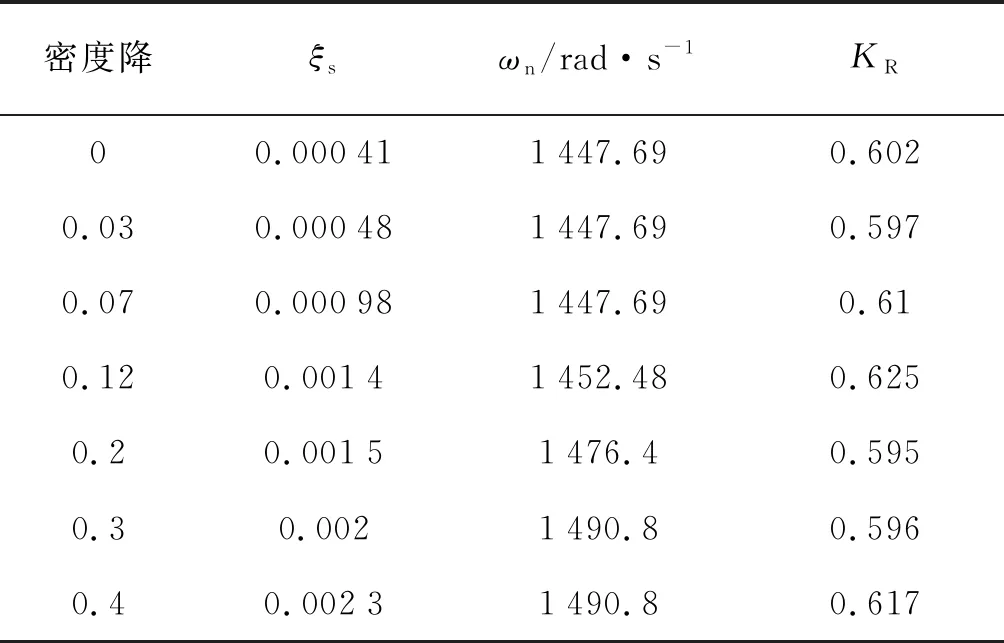
表2 水流量为30 kg/min下的模型参数Tab.2 Model parameters of water flow rate under 30 kg/min
表2中,水流量为30 kg/min,随着密度降的提升,阻尼比ξs逐渐增大,固有频率逐渐增大,稳态增益KR基本不变。
表3和表4中模型参数的变化规律与表2中类似。阻尼比的增大意味着需要更高的驱动能量,而稳态增益KR的变化情况对驱动基本没什么特殊的要求。

表3 水流量为60 kg/min下的模型参数Tab.3 Model parameters of water flow rate under 60 kg/min
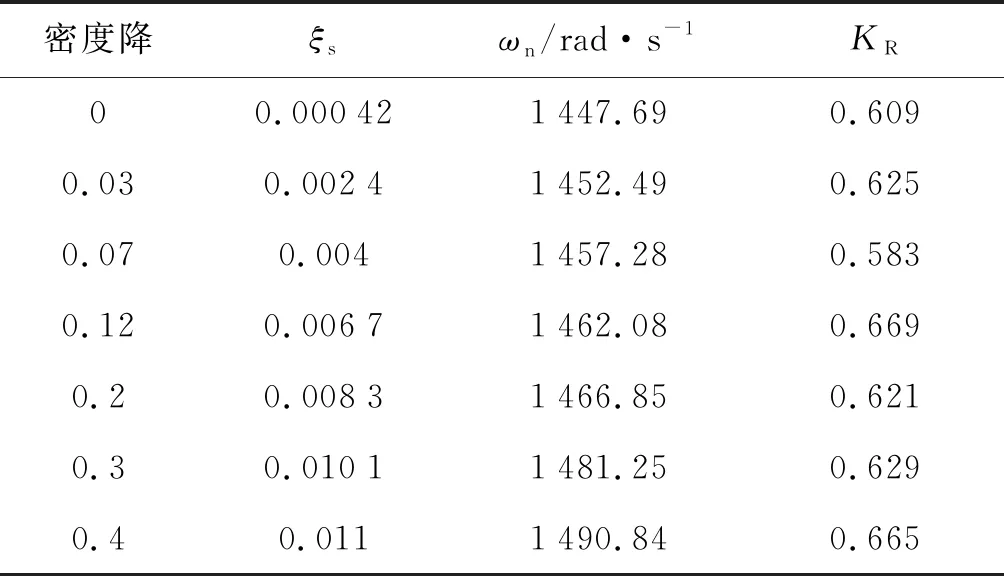
表4 水流量为90 kg/min下的模型参数Tab.4 Model parameters of water flow rate under 90 kg/min
水流量不变时,随着密度降的增大,流量管的阻尼比会逐渐变大。但是,不同水流量下,流量管的阻尼比增大情况不同。为了观察阻尼比的变化情况,给出以密度降为横坐标轴、以阻尼比为纵坐标轴的不同水流量下阻尼比的变化趋势图,如图1所示。可以看出,水流量为30 kg/min时,密度降为0.4下的阻尼比大小相较于单相流下提高了一个数量级;在水流量为90 kg/min时,密度降为0.4下的阻尼比大小相较于单相流下提高了两个数量级。同一密度降下,水流量越大,造成的阻尼比越大,需要提供更多的驱动能量。
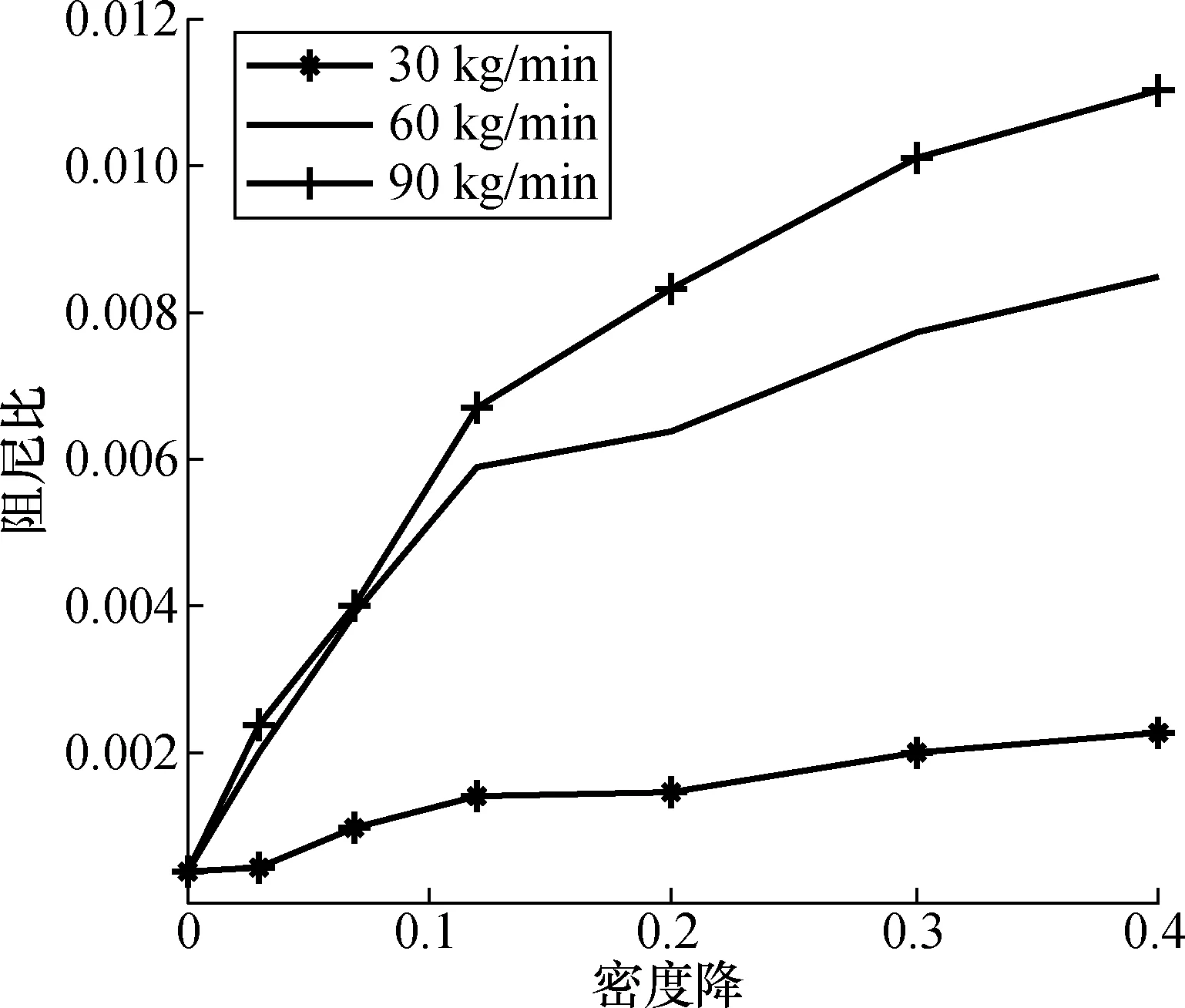
图1 阻尼比变化趋势Fig.1 Change trend of damping ratio
2.3 气液两相流下对驱动技术的要求
流量管正常工作时,一般有一个最佳振幅,流量管以这个幅值稳态振动时,能最大程度地提高一次仪表的测量性能,并延长一次仪表的使用寿命[13]。由2.1节和2.2节可得,在单相流工况下,流量管的固有频率和阻尼比较为稳定,易于维持在最佳振幅上,不需要特别的驱动技术。在气液两相流下,流体复杂,为了使流量管振动在较高且平稳的幅值状态下,需对驱动技术做相应的提升。
在气液两相流下,流量管振动频率波动较大,为了满足驱动信号与流量管振动信号的频率、相位匹配关系,需要快速地更新驱动信号;流量管的阻尼比也会急剧增加,需要及时地提高驱动能量。但是,模拟驱动采用模拟电路调节驱动信号的幅值、频率、相位,调节速度跟不上流量管固有频率与阻尼比的变化速度。因此,采用全数字驱动技术,依靠信号处理方法,直接合成相应幅值、频率、相位的驱动信号,调节速度大大增加,可以跟踪上气液两相流等复杂工况下流量管的固有频率和阻尼比波动,维持流量管振动。
3 启振技术
科氏质量流量计测量的是稳幅振动的流量管,发出的两路流量管振动信号的相位差,因此,科氏质量流量计测量的第一步工作就是将停止振动的流量管激励到其固有频率下的稳幅振动状态,这一过程即是流量管的启振。全数字驱动的启振方法有很多,本节从实现方法由易到难的角度,分析5种启振方法,并给出具体工况下启振方法选择的原则。
3.1 模拟转数字启振
文献[14]提出了一种模拟转数字启振的方法,其硬件框图如图2所示。DSP控制驱动选择电路选择模拟驱动或是全数字驱动。启振时,DSP选择模拟驱动电路,采用噪声启振。当流量管振动信号幅值达到设定值时,DSP选择全数字驱动电路,完成启振。
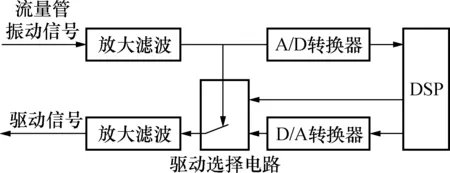
图2 模拟转数字启振硬件框图Fig.2 Analog to digital start-up hardware block diagram
模拟转数字启振采用模拟驱动启振,启振后使用数字驱动计算流量,避开了数字驱动启振难的问题。但是,本质上还是模拟驱动启振,启振时间长,不利于提升数字驱动的启振性能,且要在一套系统中实现模拟与数字两种驱动技术,性价比低。
3.2 随机波启振
文献[15]提出了一种随机波启振的方法,其启振操作流程图如图3所示。先用一个由随机数序列组成的波形激励流量管,频率在一定频带宽度内随机。激励一段时间后,流量管已经振动,但并未处于最佳振动状态。此时,停止激励流量管,让流量管处于自由衰减状态。由于流量管的频率特性相当于一个带通滤波,流量管固有频率处的波形衰减较慢,其他频率的波形衰减较快。经过一段时间后,只有流量管固有频率处的波形。用数字处理方法解析波形的频率,即可得到流量管的固有频率;再以该频率的正弦波激励流量管,完成启振。

图3 随机波启振操作流程图Fig.3 Random wave start-up operation flow diagram
随机波启振采用随机波作为自激信号,其工作原理与模拟驱动相似,将随机波作为噪声信号启振。因此,启振时间较长,不利于提升数字驱动的启振性能,同时,它还要求随机波的频带宽度较宽且必须包含流量管固有频率。
3.3 正弦波启振
文献[16]提出了一种正弦波启振的方法,先发出一个接近安全栅电压的正弦波信号驱动流量管,流量管会发出微弱的流量管振动信号。核心处理器检测到流量管振动信号后,采用数字信号处理方法,得到其幅值、频率、相位信息,合成一个更接近流量管固有频率的正弦波信号,再以该正弦波信号驱动流量管。不断重复这个过程,驱动信号频率会逐步接近流量管固有频率,流量管振动信号幅值逐步增大,直至完成启振。
正弦波启振生成的驱动信号频率逐步接近流量管固有频率,方法简单,易于实现。但是,需要知道流量管固有频率范围,初始正弦波频率与流量管固有频率相差应在100 Hz以内。
3.4 扫频方波启振
文献[17]提出了一种扫频方波启振的方法,先等间隔扫频输出连续频率的方波信号驱动流量管,利用方波信号所含的基波分量以及不同频率奇次正弦谐波分量来激振流量管。当某一频率方波与流量管固有频率接近时,检测到的流量管振动信号幅值最大,捕获此方波频率,并以此频率的方波持续驱动流量管。调用频率估计算法对流量管振动信号进行频率估计,最后以粗估得到的流量管共振频率的正弦波来驱动流量管达到稳定的工作状态。
由于从频域角度流量管可看成一个带通滤波器,当方波信号的频率等于固有频率时,流量管振动信号获得最大增益,输出幅值最大。因此,逐渐增加方波的频率,记录流量管振动信号幅值,幅值最大处的方波频率即是流量管的固有频率。扫频方波启振算法简单,但是,需要知道流量管的固有频率范围。
3.5 正负阶跃交替启振
文献[18]提出了一种正负阶跃交替启振的方法,其启振操作流程图如图4所示。用正负阶跃信号激励流量管,使流量管振动信号幅值不断增强。当其幅值达到频率估计需要的幅值a时,进入零驱动模式,估计流量管的固有频率,再以该频率的正弦波激励流量管,结合非线性幅值控制算法更新正弦驱动,完成启振。
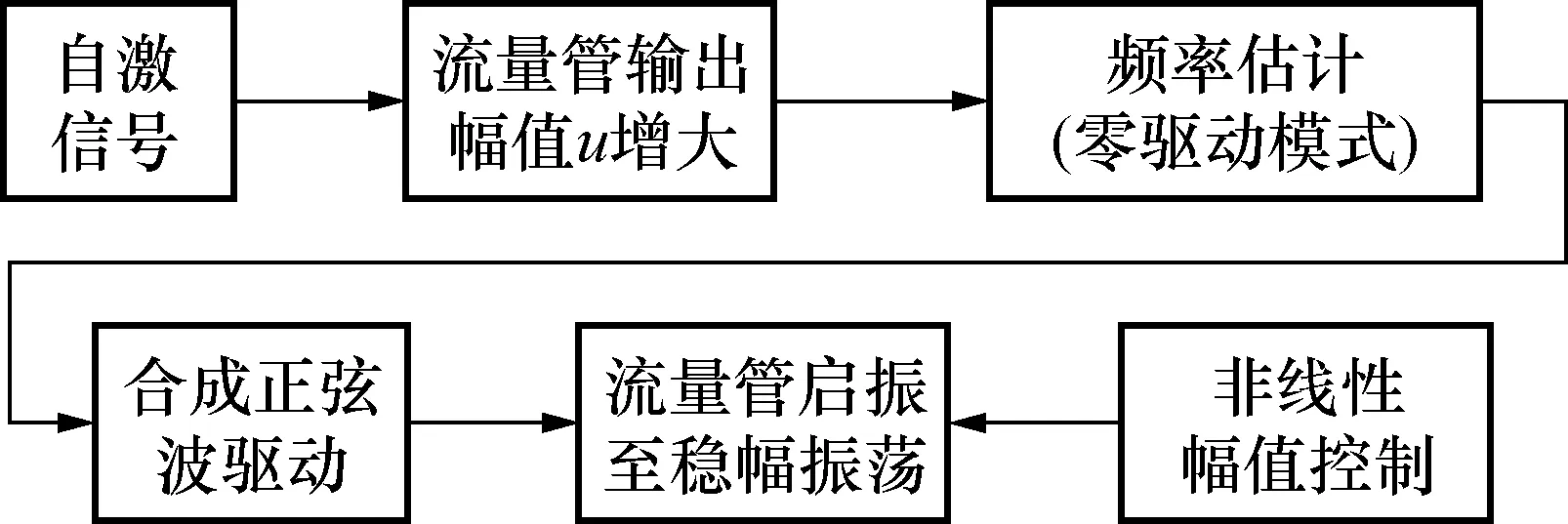
图4 正负阶跃交替启振操作流程图Fig.4 Positive and negative step alternate start-up operation flow diagram
当流量管振动信号进入(-90°+k×360°)~(+90°+k×360°)范围内时施加负阶跃,可使流量管输出信号得到加强;当信号进入(+90°+k×360°)~(+270°+k×360°)范围内时施加正阶跃,同样可使信号得到加强。因此,在信号到达(0°+k×360°)时施加负阶跃、到达(180°+k×360°)时施加正阶跃可使信号得到最大幅度加强,即在2个过零点处施加正负阶跃,能够让流量管振动信号幅值不断增强,直至增强到频率估计算法所需的幅值。正负阶跃启振无需知道流量管的固有频率范围,但算法较为复杂。
3.6 启振方法选择
根据不同的工况,可将科氏质量流量计的启振分为流量管固有频率范围已知的启振与流量管固有频率范围未知的启振。
在正常的流量测量中,流量管的固有频率范围已知,虽然其会随着流体的不同(气体、水、油等),或是流体状态的不同(单相流、气液两相流、批量流等)而发生几赫兹或几十赫兹的变化,但是,波动范围不大。此时,随机波启振、正弦波启振和扫频方波启振都可以驱动流量管完成启振。但是,随机波启振时间长,扫频方波启振较为复杂,且需要较大的缓存区存储方波频率和对应的流量管振动信号幅值。因此,可以选择正弦波启振,方法简单,启振时间短,适用范围广。
在进行新流量管的数据测试中,流量管的固有频率范围未知。此时,模拟转数字启振和正负阶跃方波启振都可以驱动流量管完成启振。但是,模拟转数字启振时间长,且要在一套系统中实现模拟与数字两种驱动技术,性价比低。因此,可以选择正负阶跃方法启振,启振时间短,频率计算准。
4 驱动参数调节技术
流量管启振后,需要正确的正弦波驱动信号,实时驱动流量管振动在最佳幅值。驱动信号由3个部分组成:幅值、频率、相位。由第2节可得,幅值若未调节好,流量管振动信号不会保持在最佳振动幅值处,幅值过小会导致流量管振动信号信噪比降低,幅值过大会导致流量管振动过于激烈,影响使用寿命;这两种情况都影响测量准确性。频率若未跟随好,驱动信号的频率不是流量管的固有频率,流量管振动幅值无法获得最大增益,驱动效率下降。相位若未调节好,相差较小会导致驱动效率下降,相差过大会导致流量管停振。
4.1 幅值调节
目前,全数字驱动的幅值调节使用最多的是非线性幅值控制,其控制框图如图5所示。logA(t)与logA0分别为流量管振动信号幅值与给定幅值取对数之后的值,两者相减后的e(t)作为误差输入到控制器C(s)中,C(s)一般为PI(比例积分)控制器,输出驱动幅值K0(t),与DDS输出Kfsinωt相乘后输入到MDAC中,进行数模转换。转换出的模拟信号u(t)经过功率放大后,驱动流量管振动[19~21]。

图5 非线性幅值控制框图Fig.5 Nonlinear amplitude control block diagram
非线性幅值控制有两类关键参数十分重要,一类是对给定信号幅值和流量管振动信号幅值取对数时,对数底数的选择[22]。在非线性幅值控制研究前期,对数底数一般选为自然常数e,而后学者发现在实际应用中,当期望值A0不同时,仍然选择e作为对数底数,会影响系统的动态响应或稳态响应。因此,文献[22]中研究对数底数的选择,发现底数的选择与设置的期望值相关,并且,期望值设置的越小,相对应的底数应该越大。另一类是针对不同流量管,控制器C(s)的比例积分参数的选择。目前,比例积分参数的选择多采用经验法,根据运行经验,设置一组控制器参数,观察幅值控制结果,进行相应修改。文献[22]中给出了不同一次仪表时PI参数确定方法。先确定一台基准表的最佳PI参数,计算被测表与基准表的稳态输出比例Kcd,再将基准表的PI参数乘以比例系数Kcd即为被测表的PI参数。
4.2 频率计算
根据信号处理域的不同,频率计算可分为频域测量方法与时域测量方法[23]。
频域测量方法的核心思想为将时域信号进行傅里叶变换映射到频域中,根据信号变换后的傅里叶系数得出信号的频率信息。如基于DFT频谱分析的测量方法[24~26]等。频域测量方法将时域信号变换为频域信号,可以有效地抑制噪声的干扰,频率计算更准确。但是,由于数字信号处理的是有限长度的离散信号,因此,不可避免地会受到频谱混叠、谱间干扰等问题的影响。
时域测量方法的核心思想为根据流量管振动信号所具有的时域特点,采用针对性的分析与处理。如基于希尔伯特变换的测量方法[27,28]、基于过零检测的测量方法[29,30]和基于相关法的测量方法[31,32]等。时域测量方法不需要对信号进行傅里叶变换,因此,与频域测量方法相比,运算量大大降低。但是,时域测量方法易受到谐波噪声和随机噪声的影响,导致测量的精度下降。
一般情况下,为了减少频率计算的运算量,减轻核心处理器的负担,应选择时域测量方法。若变送器周围有较大干扰源,流量管振动信号信噪比低,为了更精准地计算频率,应选择频域测量方法。
4.3 相位跟踪
同一时刻的驱动信号与流量管振动信号同相位时,驱动效率最高。因此,在更新驱动信号之前,需要确定驱动信号的初始相位,以满足驱动信号与流量管振动信号同相位。文献[33,34]中介绍了一种确定初始相位的方法。首先,计算ADC与硬件滤波的延时时间,再计算软件滤波与确定驱动信号幅值、频率、相位的时间。最后,当核心处理器检测到由负到正的第一个过零点时,开始进行相位匹配,确保经过匹配延时和DAC延时后,输出的驱动信号与流量管振动信号同相位。驱动信号合成时序如图6所示。
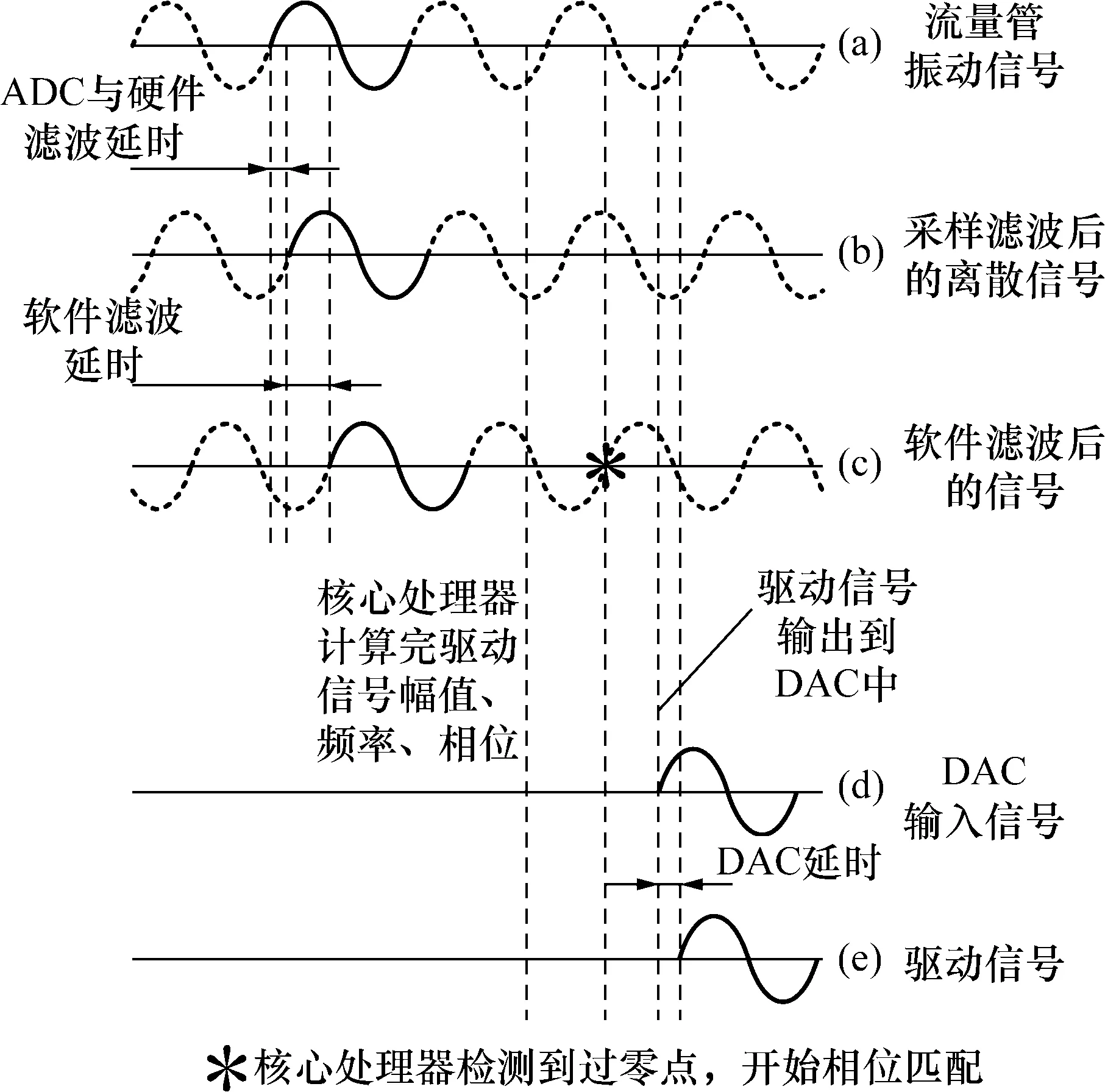
图6 驱动信号合成时序图Fig.6 Drive signal synthesis timing diagram
相位跟踪方法需要估算各种硬件延时和软件延时,与硬件电路和软件程序都息息相关,若变送器采用不同的滤波电路,或软件换了不同的滤波器、数字处理方法等,都需要重新估算驱动信号的初始相位。
5 实现方案
全数字驱动方法中,由处理器根据采集的流量管振动信号计算驱动信号所需的频率、相位和幅值信息,进而合成驱动信号后提供给电磁激振器。一般有两种结构:一种结构是由核心处理器控制外部DAC(数模转换器)直接合成驱动信号[34~37],该方式需要波形合成算法,较为复杂;另一结构是由核心处理器控制外部DDS(直接数字频率合成器)合成具有一定频率、相位且幅值固定的初始驱动信号,并由MDAC(乘法数模转换器)控制幅值[8,27,33,38,39],该方式的优点在于核心处理器只需向DDS写入包含频率、相位信息的控制字即可发出初始驱动信号,较为简单。另外,从核心处理器的数量来看,又可将实现方法分为单核全数字驱动和双核全数字驱动。
5.1 基于DSP的单核全数字驱动
单核全数字驱动中,单个核心处理器既要承担驱动任务,又要承担信号处理任务。本课题组研制的一种基于DSP的单核全数字驱动的原理框图如图7所示[33,38,39]。DSP控制ADC采集到流量管振动信号后,使用三点Lagrange插值算法计算出驱动信号的频率和相位信息,由DDS输出具有一定频率、相位和幅值的初始驱动信号;控制DDS更新信号后,DSP运用非线性幅值控制方法,通过MADC对初始驱动信号的幅值进行控制;最后经由功率放大后形成最终的驱动信号。
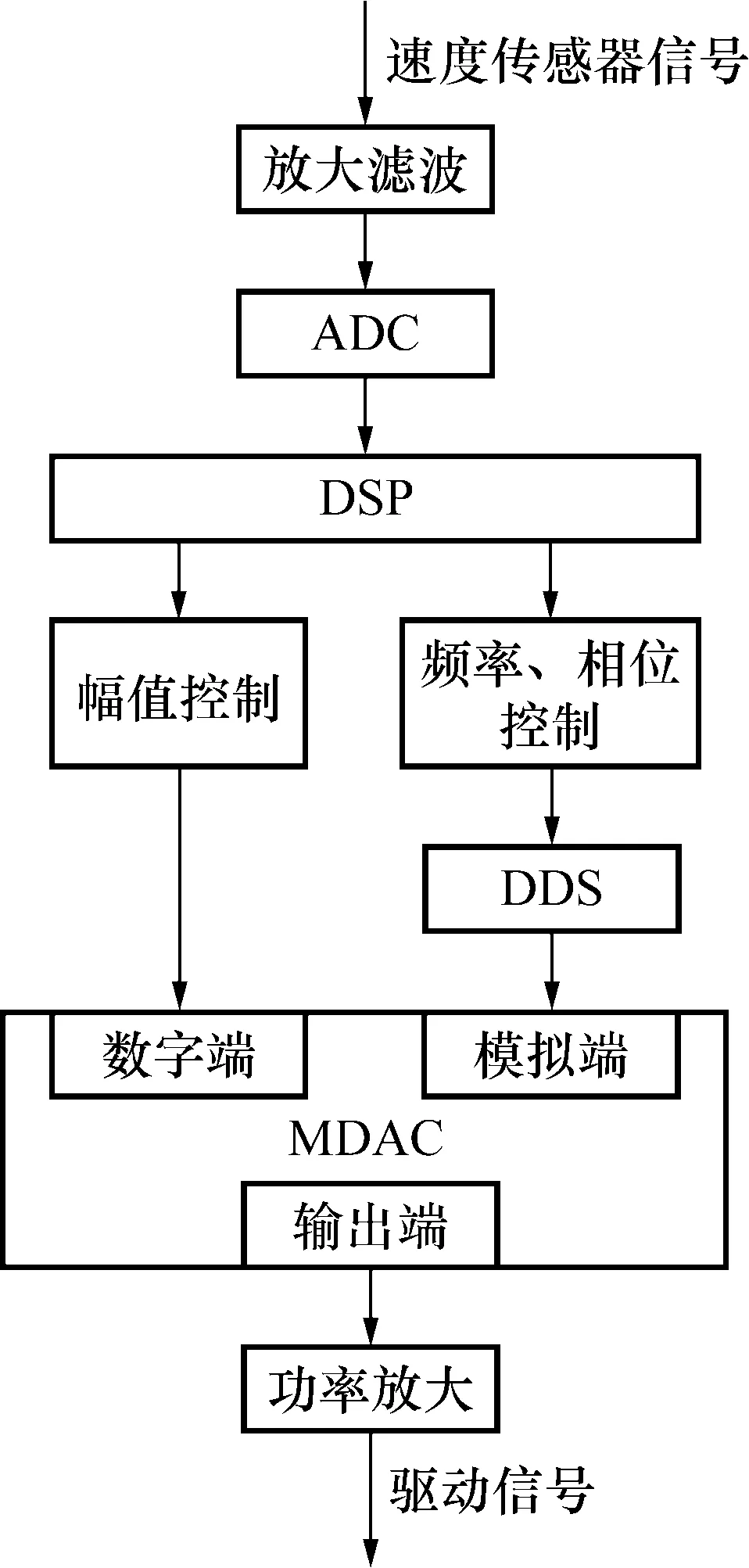
图7 基于DSP的单核全数字驱动原理框图Fig.7 Block diagram of single-core all-digital drive based on DSP
由于DSP为串行执行的处理器,所以它一次需要对一段数据进行处理,才能输出驱动信号。正常工作时,DSP不仅要执行驱动任务,还要计算质量流量和控制外设等。其控制ADC采集流量管振动信号的采样率为3 750 Hz,并且每采集到500点数据执行一次算法并更新一次驱动信号。对于固有频率为230 Hz的一诺微弯型DN25一次仪表来说,约每30个信号周期更新一次驱动信号。在平稳的单相流下,由于流体较为稳定,即使驱动信号更新周期较长,流量管也可以维持平稳振动。气液两相流下,流量管的振动状态每周期都会发生变化。过长的更新周期,会使驱动信号与流量管振动信号之间无法实时满足频率、相位的最佳匹配条件,导致流量管振动信号幅值波动较大。
5.2 基于DSP+FPGA的双核全数字驱动
在双核全数字驱动中,使用两种核心处理器,由二者共同完成驱动任务和信号处理任务[8,34,35],这种方式可以充分利用每种处理器的优势,以达到期望效果。本课题组研制了一种双核全数字驱动,由DSP与FPGA配合,DSP负责信号处理任务,FPGA负责驱动任务,其原理框图如图8所示。其中,FPGA负责控制ADC采集流量管振动信号,并将数据传输给DSP进行质量流量计算、外设控制等。与DSP通信的同时,FPGA使用三点反向Lagrange插值算法计算出驱动信号的频率和相位信息,控制DDS输出具有一定频率、相位和幅值的初始驱动信号;计算频率相位参数的同时,FPGA采用非线性幅值控制算法,通过MADC对初始驱动信号的幅值进行控制,最后经由功率放大后形成最终的驱动信号。
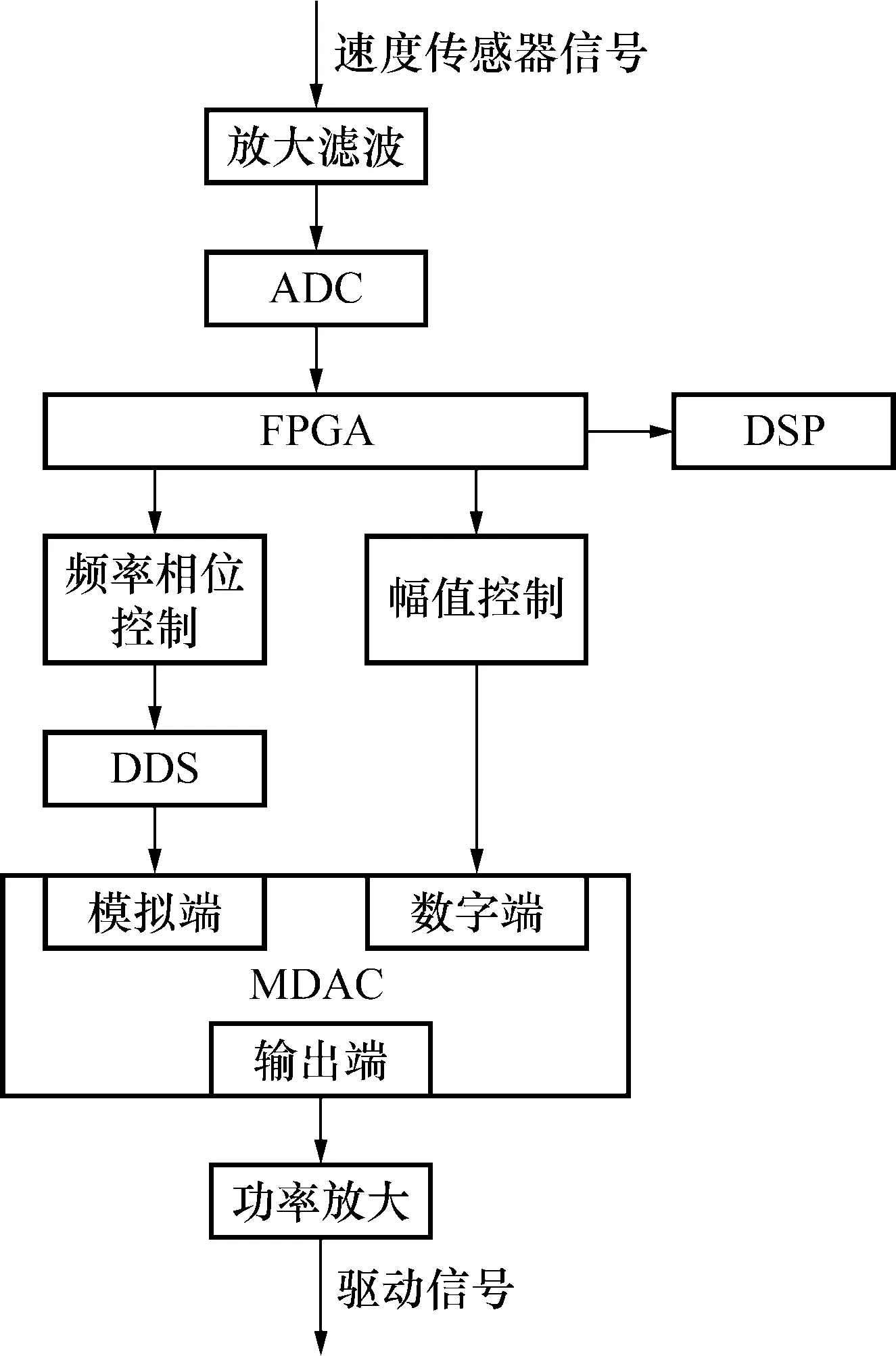
图8 基于DSP+FPGA的双核全数字驱动原理框图Fig.8 Block diagram of dual-core all-digital drive based on DSP+FPGA
FPGA具有并行执行的特性,可以同时与DSP进行数据通信和计算驱动参数,从而使驱动信号更新速度加快。流量管振动信号为正弦波,单周期内具有一个正过零点和一个负过零点。根据过零点的变化可以每半周期更新一次驱动信号。单相流下,该种全数字驱动方式可以维持流量管的正常振动。气液两相流下,由于驱动更新周期较短,即使流量管振动状态变化剧烈,也可较好地维持流量管的振动。
5.3 实现方案推荐
基于DSP的单核全数字驱动,仅需要单个核心处理器即可完成全数字驱动技术的实现,在气液两相流下维持流量管振动,只需掌握DSP技术,推广难度较低,成本较低。但是,单个核心处理器既要承担驱动任务,又要承担信号处理任务,驱动信号更新频率慢,流量管振动信号幅值波动大。
基于DSP+FPGA的双核全数字驱动,由DSP与FPGA配合,DSP负责信号处理任务,FPGA负责驱动任务,驱动更新速度快,流量管振动信号幅值波动小。但是,双核全数字驱动实现复杂,需要同时掌握DSP技术和FPGA技术,技术难度较大。
6 结束语
1) 对流量管的振动特性进行了研究。单相流下流量管振动状态简单,而气液两相流下流量管振动状态复杂。单相流工况下,流量管的固有频率和阻尼比较为稳定,易于维持在最佳振幅,不需要特别的驱动技术。气液两相流下,流量管固有频率波动较大,为了满足驱动信号与流量管振动信号的频率、相位匹配关系,维持驱动信号的波形,需要全数字驱动技术驱动流量管。
2) 分析并比较了5种启振技术:模拟转数字启振、随机波启振、正弦波启振、扫频方波启振和正负阶跃交替启振,它们的实现难度由易到难。其中,随机波启振、正弦波启振和扫频方波启振可用于流量管固有频率范围已知下的启振,正弦波启振性价比最高;模拟转数字启振和正负阶跃交替启振可用于流量管固有频率范围未知下的启振,正负阶跃交替启振性价比最高。
3) 给出了全数字驱动下,驱动信号三要素的确定方法。全数字驱动可以通过非线性幅值控制调节驱动信号的幅值、通过数字处理方法计算驱动信号的频率、通过估算硬件延时和软件延时确定驱动信号的相位,获得最好的驱动效果。
4) 对比了全数字驱动的两种实现方法:基于DSP的单核全数字驱动和基于DSP+FPGA的双核全数字驱动。基于DSP的单核全数字驱动,DSP既承担驱动任务,又承担信号处理任务,驱动更新速度慢,几十个信号周期更新一次驱动。气液两相流下,能够维持流量管的振动,但流量管振动信号的幅值波动较大。只需掌握DSP技术即可实现,且成本低,易于推广。基于DSP+FPGA的双核全数字驱动,DSP与FPGA搭配,DSP发挥运算能力强的优势,承担信号处理任务,FPGA发挥并行执行的优势,承担驱动任务,驱动更新速度快,半周期更新一次驱动。气液两相流下,驱动效果更好。需要同时掌握DSP技术和FPGA技术,实现难度大。
