基于变分模态分解和奇异值分解的频率相近信号分离方法

邢婷婷，关 阳，刘子涵，樊凤杰，孟 宗

(1.燕山大学河北省测试计量技术及仪器重点实验室，河北 秦皇岛 066004; 2.唐山工业职业技术学院, 河北 唐山 063000)

1 引 言

旋转机械故障振动信号大多是非平稳、非线性信号，如何从振动信号中提取和分析丰富的故障信息，一直是机械故障诊断的热点和难点[1,2]。经验模态分解(empirical mode decomposition，EMD)[3]作为一种常用的时频分析方法，可以自适应地将信号分解为若干个不同频段的本征模态分量(intrinsic mode function，IMF)，广泛应用于机械故障诊断中[4～6]。然而当频率比小于1.5时，EMD分解会产生模态混叠现象，不能将两个单频信号正确分离成IMF分量。当滚动轴承同时有两种或多种故障时，其振动信号的频率成分由于故障特征频率和倍频的存在变得十分复杂，两种故障的特征频率还可能十分接近，因此分离和提取故障信号中的相近特征频率具有重要实际意义[7～9]。

2014年Dragomiretskiy K等人提出一种新的信号分解方法——变分模态分解(variational mode decomposition, VMD)[10]，该方法有较强的抗噪能力，对于相近频率信号有更高的分辨率，还能够提取出较微弱的信号成分[11]。文献[12]中用VMD对滚动轴承的早期故障信号进行特征提取，取得了很好的效果；文献[13]将VMD成功应用于滚动轴承故障诊断中；文献[14]将VMD与EMD对比，证明了VMD在轴承故障诊断中具有更好的频率分辨率。

本文将变分模态分解与奇异值分解相结合，利用VMD较强的抗噪能力和对相近频率信号的高分辨率特性，以及奇异值分解能有效去除虚假频率的特点[15～19]，首先对信号进行VMD分解，然后对所有分量进行奇异值分解，通过奇异值分解检测虚假成分，实现相近频率成分的有效分离。

2 变分模态分解

VMD将输入信号分解为子带信号的离散数据，在分解过程中具有一定的稀疏属性，信号被分解为数个模态uk和中心频率ωk，分解过程为：

(1)

(2)

式中：{uk}={u1,…,uk}表示分解所得的K个分量；{ωk}={ω1,…,ωk}表示各个分量中的中心频率。

各模态分解优化算法如下：

2)采用循环n=n+1，k=1:K

(3)

(4)

采用对偶上升法：ω≥0

(5)

直到收敛满足：

(6)

3 奇异值分解理论

对于一个矩阵A∈Rm×n，必定存在正交矩阵U∈Rm×m和V∈Rn×n，使得下式成立：

A=USVT

(7)

(8)

式中：S∈Rm×n；O为零矩阵；q=min(m,n)；Δ1≥Δ2≥,…,Δq>0，Δi(i=1,2,…,q)为矩阵A的奇异值。

对信号进行奇异值分解首先要将信号构造成Hankel矩阵，令m=N-n+1，设有离散数字信号x(i),i=1,2,…，N，N是信号的长度，构造的Hankel矩阵形式如下：

(9)

分解后的所有奇异值按从大到小的顺序形成序列：

S=Δ1,Δ2,…,Δq，q=min(m,n)

(10)

奇异值的大小反映了信号的能量强弱，从而根据能量强弱的不同区分不同的信号成分[20]。

4 基于VMD和奇异值分解的信号特征提取算法

与经验模态分解(EMD)相比，VMD具有坚实的理论基础，噪声鲁棒性好，在模态分离方面也有更高的分辨力。但是在信号分解前需要设定模态分解层数和惩罚因子α，算法步骤如下：

(1)设定惩罚因子α和VMD分解层数，对信号进行VMD分解；

(2)通过奇异值分解检测虚假分量，如果虚假分量超过两个则重新设定分解层数；

(3)对分解后的各分量进行幅值谱分析；

(4)从幅值谱中提取故障特征频率。

流程图如图1所示。

图1 算法流程图Fig.1 Flow chart of algorithm

5 仿真分析

为验证方法的有效性，通过仿真信号进行分析。仿真信号表达式如下所示：

x=2(1+3sin(200 π t))sin(500 π t)+

sin(140 π t)+sin(120 π t)+n(t)

(11)

式中：n(t)为随机噪声；采样频率为1kHz；信号x的波形如图2所示。

图2 仿真信号时域波形图Fig.2 Time domain waveform of simulation signal

图3 VMD分解后各分量Fig.3 Signal components after variational mode decomposition

VMD分解时，惩罚因子α采用默认值2 000，分解层数设为6，分解后各个分量如图3所示。对每个分量进行奇异值分解，奇异值分布如表1所示。

表1 各分量的奇异值分布Tab.1 Singular value distribution of signal components

由于奇异值的时域能量聚集性，比较发现分量6的奇异值发生突变，所占能量也非常小，故判定分量6为虚假成分。为了验证奇异值检测的可靠性，对每个分量求幅值谱，如图4所示。

图4 各分量幅值谱Fig.4 Amplitude spectrum of signal components

图4中分量6的幅值谱较为混乱且幅值较小，故判定分量6为虚假成分，可以剔除。由以上仿真实验可以看出VMD经过6层过分解后可以将频率相近信号60 Hz和70 Hz的分量准确的分离开，证明了VMD经过适当的过分解有利于信号的充分分离，同时用奇异值分解可以检测出虚假成分，剔除后对实验结果没有影响。

对仿真信号用EMD分解后，同样对各个IMF分量进行幅值谱分析，如图5所示。

图5 EMD分解后各IMF的幅值谱Fig.5 Amplitude spectrum of signal components after empirical mode decomposition

由图5可以看出，信号经过EMD分解后，并没有将不同频率成分的分量有效分开，发生了模态混叠的现象，还伴有虚假分量出现，大大降低了算法的精度。

6 滚动轴承故障诊断实验研究

以美国西储大学滚动轴承故障为研究对象，采用驱动端内圈和风扇端内圈混合故障的振动信号进行实验。电机转速为1 772 r/min，振动信号的采样频率为12 kHz，采样点数为5 120点。计算得到驱动端内圈故障特征频率为159.93 Hz，风扇端内圈故障特征频率为146.10 Hz，混合振动信号如图6所示。

图6 混合振动信号Fig.6 Mixed vibration signal

用VMD将其分解，层数设置为6，分解后得到各个分量如图7所示。

图7 VMD分解后各分量Fig.7 Signal components after variational mode decomposition

对各分量求其幅值谱如图8所示。

图8中，VMD分解后各分量的频率分布较为分散且没有严重的混叠现象，有利于对特征频率的提取。用奇异值检测过分解后再对各分量进行包络谱分析，选取有用信号的包络谱如图9所示。

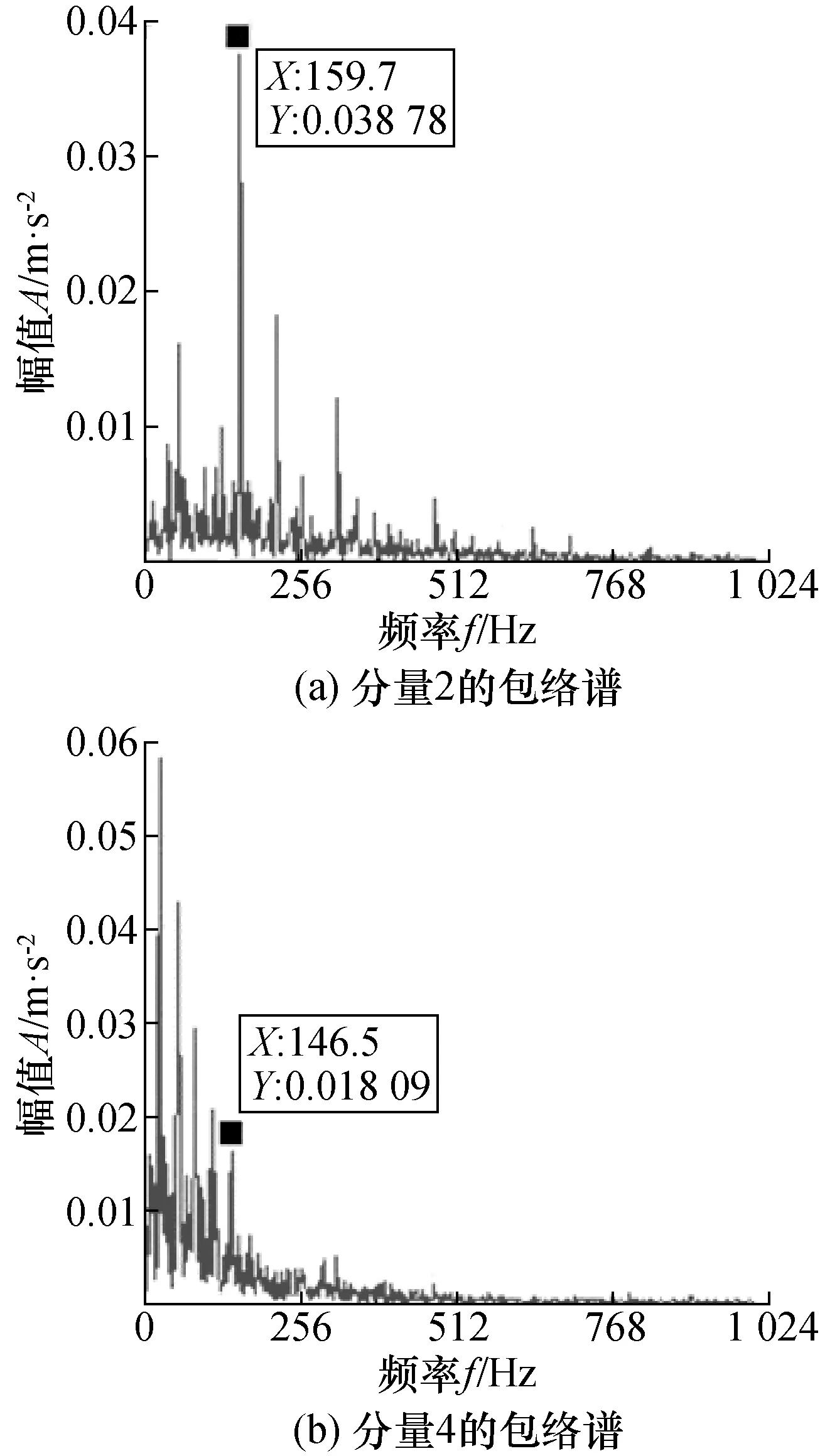
图9 VMD分解后分量的包络谱Fig.9 Envelope spectrum of signal components after variational mode decomposition

由图9包络谱可见振动信号中的驱动端内圈和风扇端内圈故障特征频率被分离开来，验证了本文提出的方法能够准确地提取出频率相近的多故障特征频率成分。作为对比，将该振动信号用EMD分解，分解后各分量的幅值谱如图10所示。

EMD分解后各分量的频率分布都有一定的重叠，大量的模态混叠对故障特征提取造成了很大干扰。对其进行包络谱分析如图11所示。

图10 EMD分解后各分量的幅值谱Fig.10 Amplitude spectrum of signal components after empirical mode decomposition

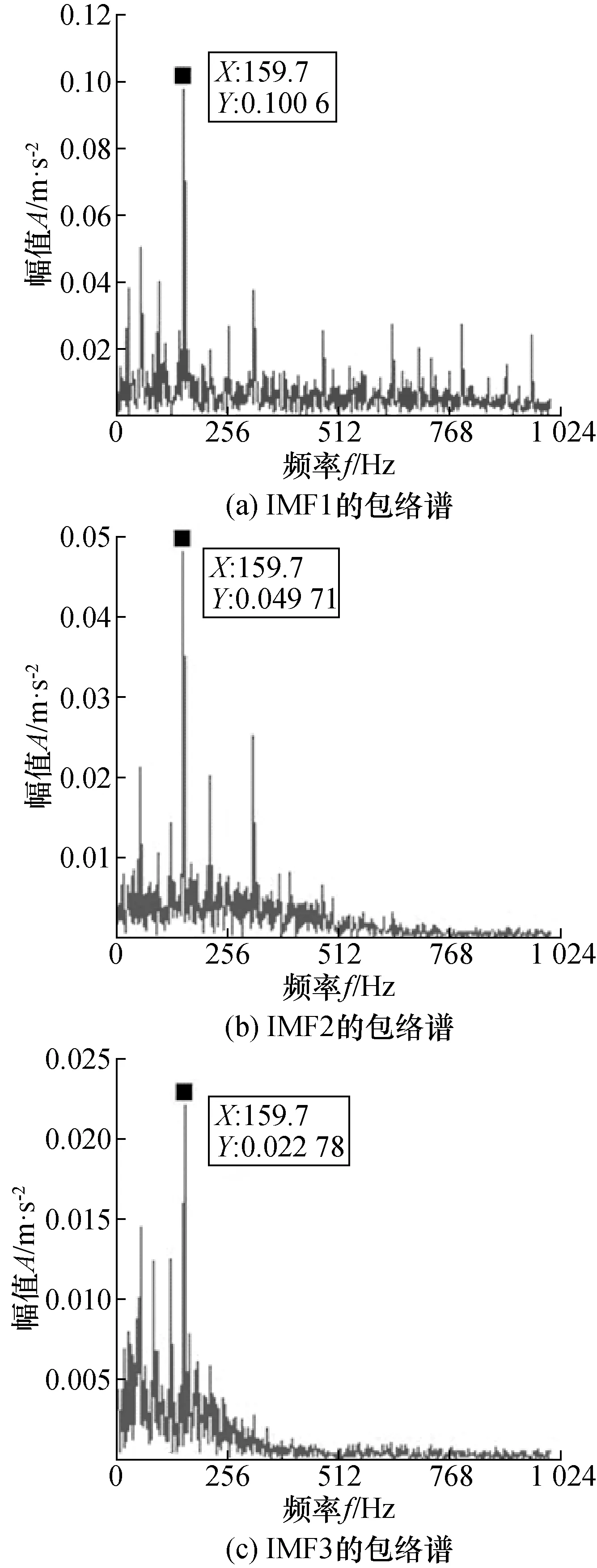
图11 EMD分解后分量的包络谱Fig.11 Envelope spectrum of signal components after empirical mode decomposition

由图11可知EMD只分离出该振动信号中驱动端内圈故障特征频率，在IMF3之后出现大量的无用频率。说明EMD不能将振动信号中的相近频率信号分离出来，不利于提取有用信号。

7 结 论

本文针对故障诊断中相近频率信号难以分离，复合故障中各类故障特征频率难以提取的问题，提出了用VMD和奇异值分解相结合的方法对原信号中的频率成分进行分离提取。通过仿真实验证明了该方法对于相近频率信号提取有非常好的效果；又通过复合故障数据实验成功提取出了不同的故障特征频率，相比于EMD方法有更高的分辨率，也有很好的抗噪能力。对于推动VMD在旋转机械故障诊断工程实际应用中有一定的价值。