基于射线照相的X射线衰减系数测量方法研究

喻拓夏，奚 清，杨 丹

(中国工程物理研究院, 四川 绵阳 621900)

1 引 言

X射线在物质中的衰减系数μ是一个重要的物理量，是射线照相探伤中参数选择的一个重要参考指标；在放射医疗[1]、射线工业探伤屏蔽材料种类及厚度选取、材料半值层计算[2]等方面具有重要意义。

衰减系数μ值描述的是射线与物质相互作用的概率[3]，受射线的能量、作用材料的原子序数A和密度ρ等因素的影响。日本学者用高灵敏度的探测器放置于射线机窗正下方，用光阑将射线约束成窄束射线，改变试件厚度进行多次透照，根据测试结果可绘制出吸收曲线，再通过计算可得衰减系数[4]。这种方法对探测器的要求很高，且操作复杂、数据处理困难。王同权等根据EPDL光子截面数据库编辑了一套计算程序，可计算出X射线的衰减系数[5]，但该方法计算复杂，编程难度较高。张小海等用Newton-Cotes梯形数值计算方法，结合Matlab软件模拟计算得出了X射线强度衰减的理论近似算法[6], 但该方法的核心公式推导复杂，变量多，梯形公式的多步差值误差较大。

在射线照相中，底片黑度与曝光量有很好的线性对应关系。因此，基于X射线照相法，提出了一种快速计算X射线在物质中的衰减系数μ值的方法。

2 理论分析

X射线照相原理是一定强度的入射X射线，通过被检物质产生一定程度的衰减后作用于底片上，在底片上形成一定的感光度。根据作用在底片上的射线强度，经过显影、定影处理后，不同感光度的底片上可显示出不同的黑度值D。

在射线照相中，管电压与射线能量有良好的对应关系：X射线管发出的光子最大能量Emax由管电压U决定，有如下关系：

(1)

式中：h为普朗克常量；c为光速：e为电子电荷量；λmin为X射线最短波长。

在实际检测中，起主要作用的部分是连续谱中最大强度波长临近的射线[7]。照射到胶片上的射线进行过滤波，随着工件厚度的变化，线质和衰减系数变化很小。而滤波后的射线在X射线光谱中的分布应为从最大强度附近处到最短波长的范围。文献[8]中以平均波长λ来简化，并认为：

λ=φλmin(φ=1.1～1.8)

2.1 胶片特性曲线

胶片特性曲线是表示曝光量与底片黑度之间的关系曲线，用横坐标表示X射线曝光量的对数值，纵坐标表示胶片显影后所得的黑度。增感型胶片特性曲线如图1所示，cd段为曝光正常区，黑度值与曝光量对数值成正比关系。在X射线照相过程中，主要关注点就在该区域。

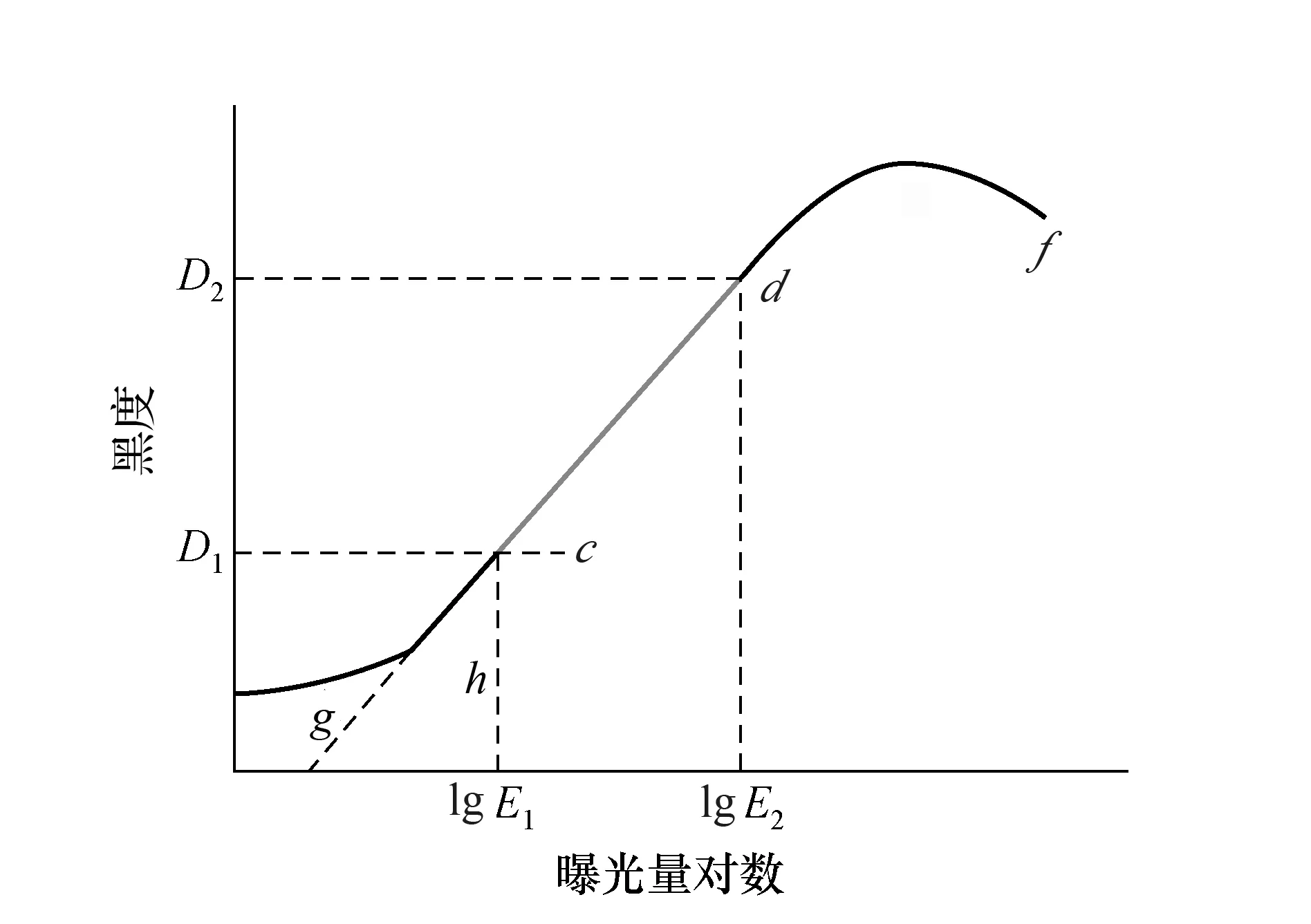
图1 增感型胶片特性曲线Fig.1 Characteristic curve of screen-type film

可以用函数表示曝光正常区cd段：D=klgE+c，其中k，c为常数。该式可写成：

E=10aD+b

(2)

用相同电压U和不同曝光量E1和E2对厚度为T的试块进行两次拍照，得到的黑度值为D1和D2的两张胶片，这两组数据对下式成立：

E1e-μT=10aD1+b

(3)

E2e-μT=10aD2+b

(4)

D1、D2可通过黑度计测得，E1、E2为设定值已知，联立式(3)、式(4)可得：

(5)

2.2 μ值计算

a值求得后再通过两次拍照求得该材料的衰减系数μ值。用相同电压U和相同曝光量E对厚度分别为T1、T2的同一材质的试块进行两次拍照，得到黑度为D1、D2的两组胶片，则这两组数据满足以下关系：

10aD1+b=Ee-μT1

(6)

10aD2+b=Ee-μT2

(7)

其中:D1、D2可通过黑度计测得，T1、T2也易测得，联立式(6)、式(7)可得：

(8)

3 实 验

为了论证该方法的有效性，用标准钢台阶试块做了射线照相实验，并对实验数据进行了分析。

3.1 实验条件

3.1.1 标准钢射线透照

为得到多组黑度值以选择最佳黑度，对钢质台阶试块进行透照，台阶厚度分别为：8～15 mm(相邻台阶厚度差为1 mm)；在曝光量为10 mA·min的条件下，分别用140、130、120 kV的管电压进行了透照；在曝光量为15 mA·min的条件下，分别用140、130 kV的管电压进行了透照，用黑度计测得底片黑度值，并将数据进行了处理和分析。

3.1.2 原始数据分析

测出黑度值后作出D-T散点图，并分别进行了一次函数、二次函数，三次函数拟合，拟合结果如图2所示。

比较三次拟合结果发现：一次拟合所得方程标准偏差η=0.017，二次拟合所得方程标准偏差η=0.007 4，三次拟合所得方程标准偏差η=0.003，根据文献[8 ]可知，标准偏差越小预判的线性变化趋势越准确。可见原始数据的变化趋势最接近于三次函数。这是由于黑度区间包括了曝光不足区和曝光补偿区，在这段区域内黑度值与相对曝光量不是一次函数变化关系。为此，需找出数据的可信任区间。

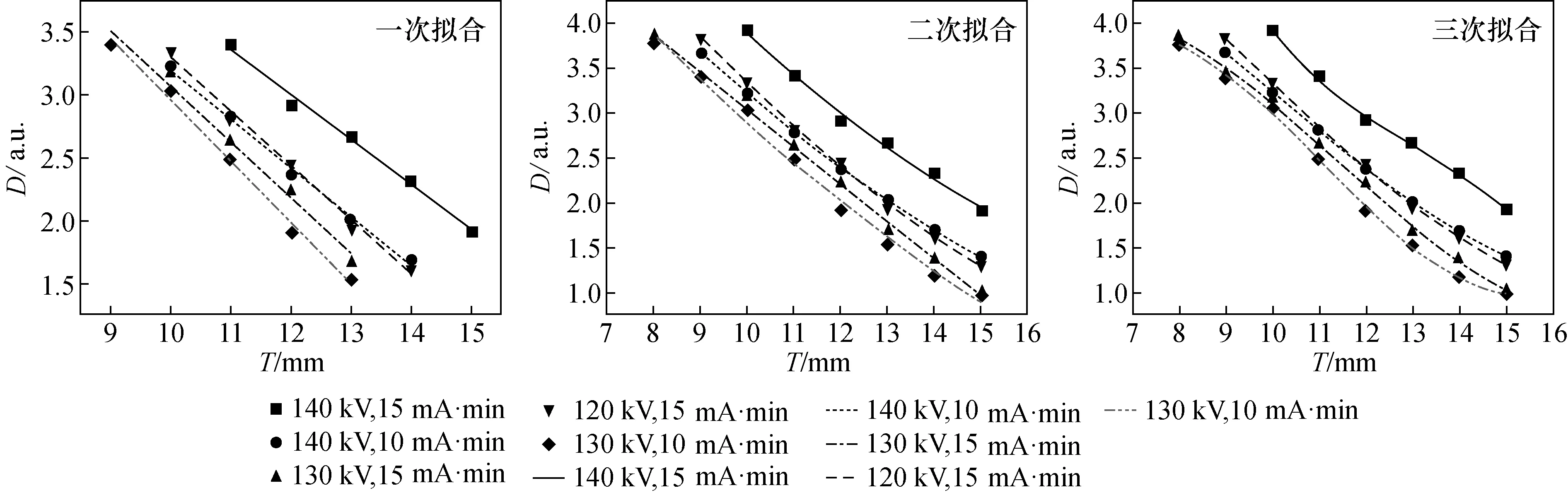
图2 原始数据进行一次拟合、二次拟合、三次拟合曲线结果Fig.2 Results of primary fitting, secondary fitting and cubic fitting curves of original data

3.1.3 可信区间数据分析

反复去除前后的几个点并进行拟合后，发现原始数据中黑度值小于1.5的数据可能处于胶片特性曲线中的曝光不足区；黑度值大于3.5的数据可能处于曝光过度区或反转区。将该区间内的数据剔除，并对剔除后的散点图进行拟合，拟合结果发现，一次拟合所得方程标准偏差η=0.011，二次拟合所得方程标准偏差η=0.017，三次拟合所得方程标准偏差η=0.02。

可见，在曝光正常区内，D-T曲线最接近于直线拟合，这与王玉玲等人的研究结果吻合。因此，射线照相法获得射线衰减系数实验中黑度值的可信任区间为1.5～3.5。可信区间的D-T曲线一次拟合结果如图3所示。

根据图3中的拟合结果，将该斜率绝对值变化情况进行作图比较，见图4。

图3 可信任区间内钢的一次函数拟合D-T图Fig.3 Primary function fitting of steel in the trusted interval D-T diagram

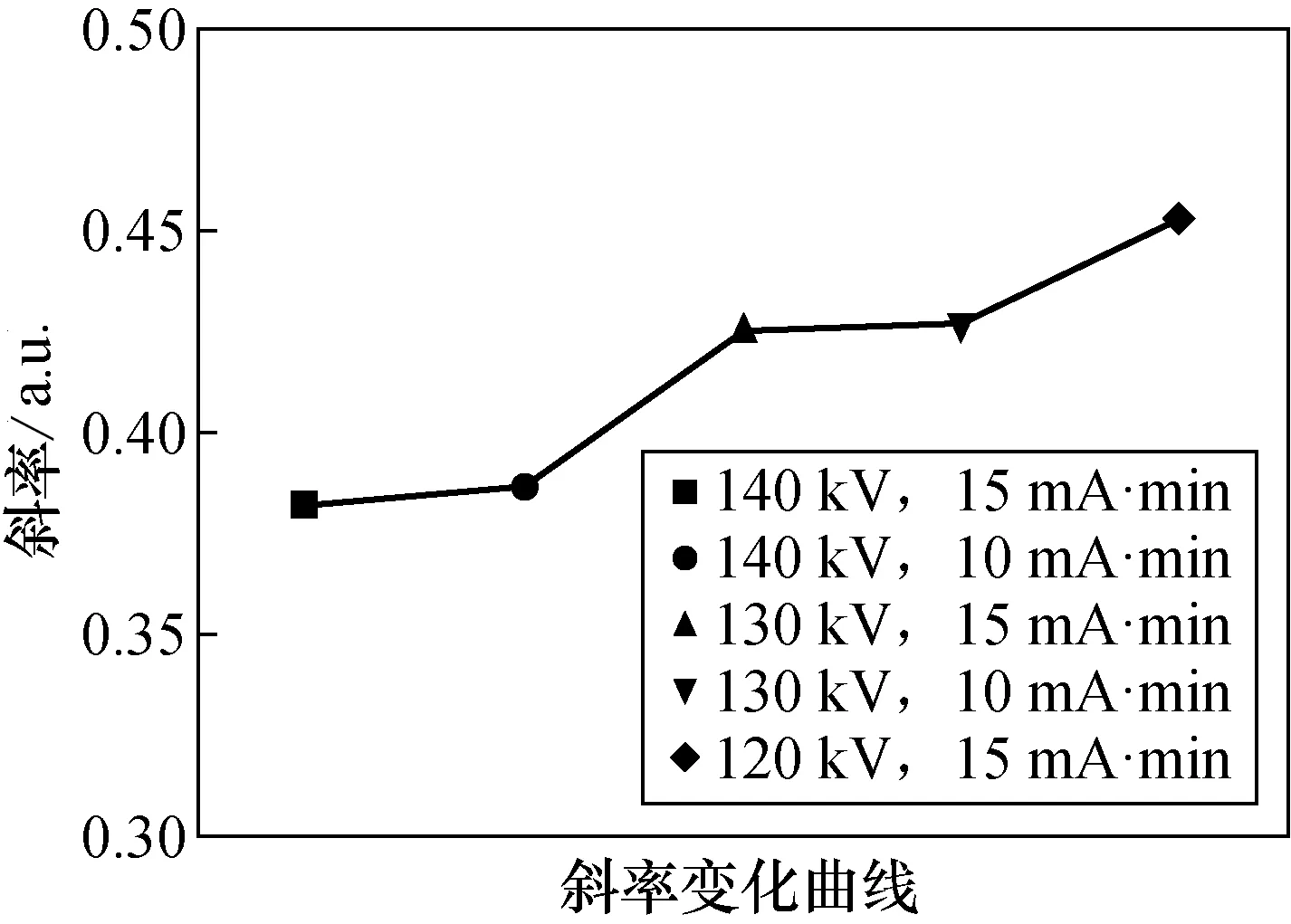
图4 一次函数拟合图中的斜率变化图Fig.4 Slope change diagram in the curve fitting function

图4显示：管电压相同时，直线斜率绝对值基本相同，可见当管电压不变时，曝光量的增减不会影响衰减系数。随着管电压增加，直线斜率绝对值逐渐减小，说明管电压越高，射线的衰减系数越小，这与射线衰减规律相符。

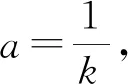
将实验数据代入式(9)求得了140、130、120 kV管电压下钢质台阶试块的μ值，如表1所示。

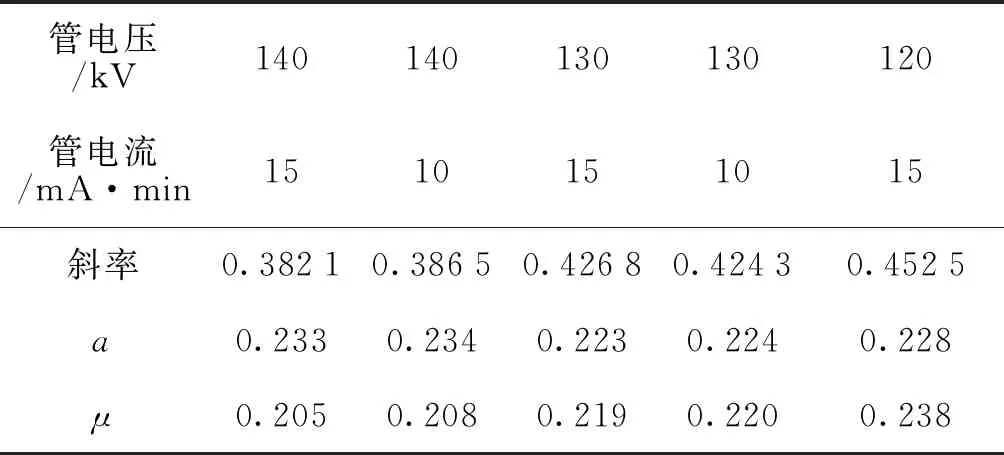
表1 实验测得不同管电压下钢的X射线衰减系数Tab.1 Experimental measurement of X-ray attenuation coefficients of steel at different tube voltages

将实验值与理论值对比如图5所示[10 ]。

图5 标准钢衰减系数实验值与理论值对比图Fig.5 Comparison of experimental value and theoretical value of attenuation coefficient of standard steel

由图5可见，实验算得的μ值与理论值非常接近，以理论值为标准，可算得误差<3%，误差可能来源于黑度计的读数误差、胶片感光的统计涨落等。

3.2 标准铝射线照相

为避免单一材料的偶然性，对标准铝阶梯试块进行了射线照相实验，台阶厚度为28～40 mm(相邻台阶厚度差为2 mm)，管电压选用为：91、93、95、97 kV。将测得的数据中黑度值在1.5～3.5范围内的点进行了一次拟合，如图6所示。

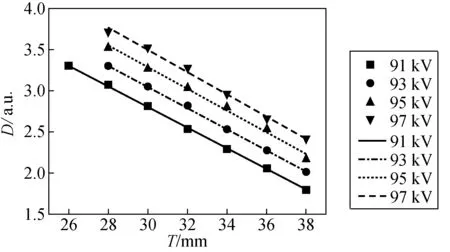
图6 不同管电压下铝的D-T关系一次拟合图Fig.6 Primary fitting diagram of D-T relation of aluminum at different tube voltages

图6显示：标准铝D-T关系的一次拟合标准偏差极小，说明在可信区间内标准铝的D-T曲线也是一次函数。可见式(8)同样适用于铝的衰减系数求值。

将实验数据代入式(8)算得了标准铝阶梯试块在不同管电压下的X射线衰减系数如表2所示。

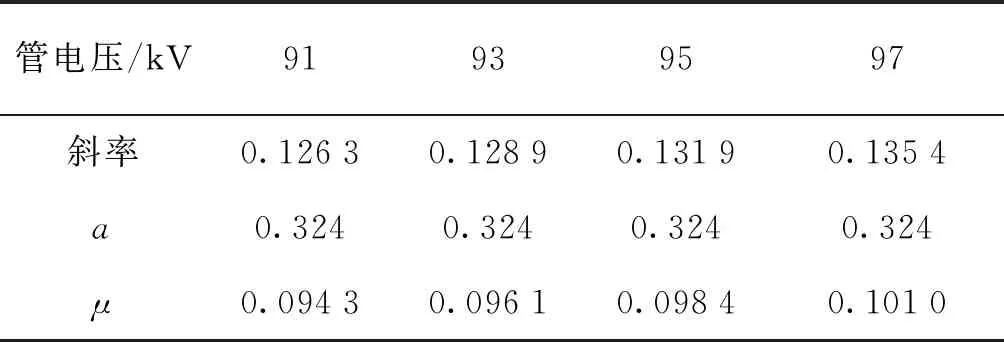
表2 不同管电压下铝阶梯试块的X射线衰减系数Tab.2 X-ray attenuation coefficients of stepped aluminum specimen at different tube voltages

表2所示铝的衰减系数与杜继星等在铝半值层计算中得出的衰减系数相符[11]。在实际应用中，只需取可信区间内的任意两点来进行D-T曲线斜率的计算即可，这样可省去数据拟合的过程，其误差也只是增加了胶片感光的统计涨落带来的误差，可控制在较小的范围内。在对其它材料进行μ值测量时，也只需要选择合适的透射条件，得到落在可信区间内的点进行计算。

4 结 论

(2) 证明了D-T曲线在可信区间内接近于直线，并得出了黑度值可信区间为1.5～3.5。

(3) 基于射线照相法测得了管电压为140、130、120 kV下标准钢的μ值，与理论值对比误差<3%。测得了管电压为91～97 kV下铝的μ值，与理论值相近。证明了射线照相法求μ值的可靠性和普遍性。