多阵列中非圆信号借助于降维搜索和子空间数据融合的直接定位算法

张小飞，曾浩威，郑 旺，李建峰

（南京航空航天大学电子信息工程学院，南京，211106）

引 言

众所周知，无线定位技术是现代信号处理中的一个重要研究领域，军事国防、地震勘探和工业生产等领域都离不开它的发展。随着国防技术的不断突破和创新，对辐射源目标定位技术的要求也不断提高[1‑2]。传统的定位模式大多数是两步定位模式，即先从原始接收信号中提取出包含目标位置信息的中间参量，如到达角度、到达频差和到达时间差等，然后结合这些参数并根据几何关系进行目标位置的交叉定位解算[3‑5]。该方法中各观测站独立进行中间参数估计，然后将参数发送至同一中心站，“目标‑参数”匹配后结合相应算法完成定位解算，原理简单，易于工程实现。

然而，传统二步定位的方式存在一些不足。从原始观测数据到目标位置估计的过程中，经历的中间处理环节越多，损失的信息就越多，后续的定位精度也会受到影响。此外，多目标情况下存在“目标‑参数”关联问题[6‑7]，任何一个参数关联错误，都将使后续定位精度急剧下降。为了避免传统二步定位体制的问题，近些年国内外学者们提出了一种新型定位技术——直接定位(Direct position determina‑tion, DPD)技术[8]。该方式的原理是直接从观测数据中估计目标位置，无需额外估计任何中间参量，因而也叫单步定位。由于直接利用原始观测数据，充分利用了目标信息，且有效避免了目标与参数关联的步骤，大大提升了对目标的定位精度，信噪比较低时仍能获得不错的估计性能。

相比于传统二步定位方法，直接定位方法复杂度太高，且对通信带宽要求较高，因此在其提出之初发展缓慢。然而，随着近些年计算机与通信技术的快速发展，制约其发展的主要因素不再是带宽和计算能力。

现有直接定位算法大多是针对未知信号进行研究的，而从信息论的角度来讲，所能利用的原始信息越多，理论上算法的性能就越好。研究表明，在建立算法模型时考虑目标源的信号特征能够进一步提升定位精度。针对常用于现代通信系统中的正交频分复用信号，文献[9‑10]提出了基于最大似然的DPD 算法；为降低算法复杂度，提升算法的实用性，文献[11]在此基础上提出了一种改进的DPD 算法。此外，针对恒模信号，文献[12]利用其恒包络特征，构建最大似然估计模型，提出了一种针对恒模信号的DPD 算法。

除了上述两种信号类型，调幅信号、二进制相移键控、脉冲幅度调制信号、正交相移键控信号等都是现代通信系统中不可或缺的信号形式，而它们都属于非圆(Non‑circular, NC)[13]信号类型。因此有关NC 信号定位算法的研究具有重要的实际应用意义。本文在文献[14]的基础上，利用辐射源信号的NC特性扩展空间信息获得增大的虚拟阵列孔径与更多的可识别信源数，然后结合子空间数据融合(Sub‑space data fusion, SDF)算法的思想，推导了针对 NC 信号的 SDF 形式的 DPD 算法(Non‑circular sub‑space data fusion，NC‑SDF)；但是由于NC 相位导致的高维搜索大大增加了算法求解时的复杂度，因此本文引入文献[15]的降维(Reduced‑dimension, RD)搜索思想，提出了降维后的子空间数据融合算法(Re‑duced‑dimension subspace data fusion，RD‑SDF)。仿真结果表明，相比于传统 SDF 算法、Capon 算法和传统二步定位算法，RD‑SDF 算法具有更高的定位精度和空间自由度；且通过降维方法，RD‑SDF 算法在保证估计性能的同时显著降低了算法复杂度。

本文主要贡献可以概括为：（1）将NC 信号特征引入到直接定位算法模型中，根据其椭圆协方差不为零的特点扩展空间信息，并结合SDF 的思想，推导了NC‑SDF 算法。相比于传统SDF 算法，NC‑SDF算法的定位性能更优，且具有更大的阵列孔径和空间自由度。（2）由于NC 相位导致的高维搜索大大增加了算法求解时的复杂度，本文通过RD 方法，去除了NC‑SDF 算法求解时的NC 相位搜索维度，提出了RD‑SDF 算法，在保证估计精度的前提下，降低了算法复杂度。

1 数据模型

1.1 多阵列联合定位模型

考虑如图1 所示的定位场景，假设已知二维x‑y平面内存在Q个互不相关的远场窄带非圆信号入射到L个位置且装有沿x轴水平放置的M元均匀线阵的观测站，阵元间距d=λ2，目标信号源位置分别位于pq=[xq,yq]T(q=1,2,…,Q)，L个观测站分别位于ul=[xul,yul]T(l=1,2,…,L)。

假设信号包络变化为慢起伏，则各信号到达观测站时的信号包络近似相等。于是第l(l=1,2,…,L)个观测站接收到的第k(k=1,2,…,K)个采样快拍时刻对应的接收信号复包络rl(k)可以表示为[14]

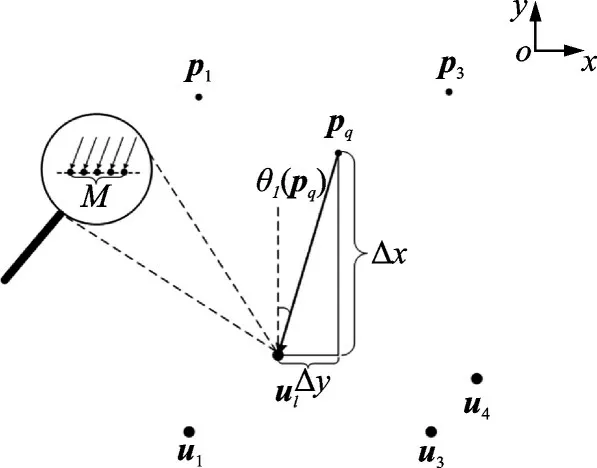
图1 多阵列联合定位场景图Fig.1 Location scene of multiple arrays

式中:sl,q(k)表示第q个信号源在第l个观测站的第k个采样快拍时刻的信号波形,nl(k) ∈CM×1表示第l个观测站的天线阵列的噪声矢量，满足文献[14]中的高斯白噪声模型假设,al(pq)为方向矢量，由信号到达方向θl(pq)决定，即

将式(1)用矢量形式表示，得到

式中

1.2 非圆信号模型

根据文献[13]可知，对于复圆信号随机矢量sl(k)来说，协方差矩阵E[sl(k)sHl(k)]≠0，但椭圆协方差而对于非圆信号随机矢量来说，二者都不为零。且对于非圆信号来说，其协方差矩阵和椭圆协方差矩阵满足

式中，φ为非圆相位，ρ为取值在0～1 的非圆率。

非圆率为1 的信号叫做最大非圆率信号。为了简单起见，本文假设非圆率均为1。根据文献[16‑19]，非圆信号可表示为

式中

2 非圆信号直接定位算法

根据信号的非圆特性这一先验信息，构建非圆信号定位模型，再结合SDF 的思想，得到NC‑SDF 算法的代价函数。考虑到算法求解时需要进行高维谱峰搜索，本文引入文献[15]中的降维思想，去除非圆相位搜索维度，最终得到RD‑SDF 算法。

2.1 子空间数据融合算法

根据式(10)，式(4)等价为

式中

为源信号矢量的幅度，是一个实值矢量。

利用非圆信号的椭圆协方差矩阵不为零的特点，可将接收信号矢量扩展为[20]

又由式(10)可得

则式(15)可以表示为

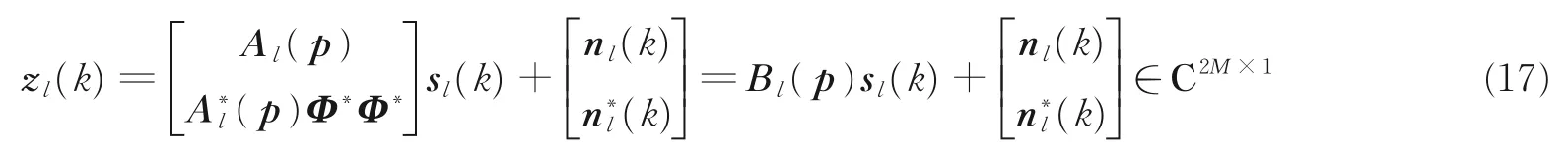
式中

式中，bl(pq) ∈ C2M×1为扩展阵列流形矢量。

将第l个观测站所有采样快拍的扩展接收信号矢量综合起来，得到扩展接收信号矩阵Zl

一般通过式（21）估计接收信号协方差

SDF 算法本质上是多重信号分类算法的扩展[21]，其原理为综合所有观测站的噪声子空间来估计目标源位置，因此需要先进行子空间分解。

对R̂l进行特征值分解，得

若用λm(m=1,2,…,2M) 表示按从大到小排序后的特征值，对应的特征向量用em(m=1,2,…,2M)表示。则式（22）中，信号子空间噪声子空间Σl为以特征值为元素的对角矩阵，即Σl=diag{λ1,λ2,…,λ2M}。

相比于圆信号，针对非圆信号的算法就需要考虑非圆相位的影响，为保证定位精度，求解目标源位置时还需要对非圆相位进行估计。同时对位置p和φ进行搜索，得到NC‑SDF 算法的代价函数

式（23）峰值对应坐标即为目标源位置及非圆相位的估计值。由于对接收信号矢量的扩展本质上增大了阵列孔径，因此理论上NC‑SDF 算法可比一般的SDF 算法估计更多信源，具有更大的空间自由度。但该算法求解时需要同时对位置(x,y)和φ进行搜索，是个三维搜索问题，复杂度很高。

2.2 降维直接定位算法

为了降低算法复杂度，提高算法的实用性。本文在文献[14]的基础上，引入降维思想，在保证原有估计性能的前提下，减少搜索维度，提出了RD‑SDF 算法。

由于(k)为实值矢量，显然有

根据式(13，24)，式(15)中的扩展接收信号矢量zl(k)可表示为

式中

令

则

为扩展流形矢量，包含了第q个目标源的位置信息与非圆相位信息。

对式(29)进行矩阵转换，使位置信息与非圆相位信息分离

式中

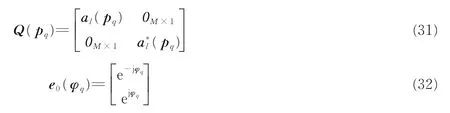
于是得到第l个观测站的子代价函数

显然，有

对于未知参数φ来说，式(35)是个二次优化问题。令e=[1,0]T，则eHg(φ) =1，于是重构式(35)的优化问题

为求解上述优化问题，拟采用拉格朗日乘子法，于是构造以下函数

式中，λ为乘子。令式（37）对e0(φ)的导数为零，即

则

又因为eHg(φ) =1，因此μ= 1 ( )eHJl(p)-1e，于是

根据式(39，40)，得到降维后第l个观测站的子代价函数

根据文献[22]，理论上当位置矢量p处于目标源位置时1,2,…,L)二者满足正交关系，若考虑噪声影响，此时对于所有观测站来说，式(41)都取得极大值。于是构建RD‑SDF 的代价函数为

至此，在保证原有精度的前提下，通过二次优化问题的求解，实现了式(23—42)的等价转换，减小了搜索维度，进而降低了算法复杂度。

观察比较式(23)和式(42)可以发现，降维前后的代价函数只是通过矩阵变换和替代实现，其本质是利用二次优化问题去除非圆相位搜索维度，先估计得到目标位置p̂，再通过式(40)求解非圆相位，并未舍弃非圆相位，因此式(23)和(42)是等价的。

2.3 算法主要步骤

上述推导已经给出RD‑SDF 的定位求解过程，算法主要步骤如下：

(1)根据式(15)扩展接收信号矢量，进而得到扩展接收信号矩阵Zl；

(3)根据式e=[1,0]T和式(35)构造代价函数fRD‑SDF(p)；

(4)将目标位置搜索区域划分为若干个二维平面网格，计算每个格点对应的代价函数值，峰值处对应的坐标即为目标源位置估计值 (x̂q,ŷq)(q=1,2,…,Q)。

3 性能分析

3.1 复杂度分析

本文算法复杂度分析如下：M表示阵元数，Q表示信源数，L表示观测站数，K表示快拍数，全局搜索时x方向划分为Lx等份，y方向划分为Ly等份，非圆相位划分为Lφ等份。本文的降维前算法主要由协方差矩阵Zl的计算、特征值分解以及搜索谱函数计算3 个步骤构成，对应的计算复杂度分别为4LKM2、8LM3和 4M2(2M-Q) +4M2+2M，因 此 NC‑SDF 算 法 总 复 杂 度 为 4LKM2+8LM3+LLx Ly Lφ[4M2(2M-Q)+4M2+2M]；相比而言，降维后算法不同之处在于，一次谱函数计算复杂度为4M2(2M-Q) +8M2+8M+14 且搜索维度仅包含x和y两个维度，因此RD‑SDF 算法总复杂度为4LKM2+8LM3+LLx Ly[4M2(2M-Q)+8M2+8M+14 ]；此外，文献[21]的传统 SDF 所需复杂度为LKM2+LM3+LLx Ly[M2(M-Q)+M2+M]，文献[23]的Capon 算法所需复杂度为LKM2+LM3+LLx Ly[M2+M]，传统二步定位算法所需复杂度为LKM2+LM3+4LQ2(M-1) +10LQ3。从复杂度可以看出，由于去除了非圆相位搜索维度，降维后算法复杂度显著降低。相比于传统SDF 算法、Capon 算法和传统二步定位算法，所提RD‑SDF 算法复杂度虽然更高，但具有更高的估计精度和空间自由度。

3.2 优点总结

综上所述，本文提出的RD‑SDF 具有以下优点：

(1)相比于传统SDF 算法、Capon 算法和传统二步定位算法，所提算法的定位精度更高。

(2)相比于传统SDF 算法和传统二步定位算法，本文所提算法可同时估计更多信源，具有更高的空间自由度。

(3)RD‑SDF 算法通过引入降维思想，在保证估计性能的前提下，去除了非圆相位搜索维度，实现了三维搜索到二维搜索的转变，算法复杂度较低。

4 仿真结果

仿真实验中，算法的估计性能分析通过计算求根均方误差(Root mean squares error, RMSE)来完成，RMSE 的定义为

式中，MN=300 为 Monte Carlo 仿真实验次数，Q为目标信号源个数，(x̂q,mn,ŷq,mn)表示第q个目标源位置在第mn次仿真实验中的估计值，(xq,yq)为第q个目标源的真实值。

假设目标源个数Q=3，分别位于p1=[-800,800]，p2=[0,500]和p3=[500,700](单位为 m，下同)，非圆相位φ=[30∘,60∘,45∘]，观 测 站 数L= 5 ，分 别 位 于u1=[-1 000,-500]，u2=[-700,-200]，u3=[-200,-500]，u4=[100,-300]和u1=[900,-700]，具体位置示意如图2所示。

仿真1探究阵元数和目标源数相等条件下本文RD‑SDF 算法的定位性能。仿真过程中，采样快拍数K=200，阵元数M=3，信噪比为15 dB，图3 给出了算法定位散点图。从图3 可以看出，即使在阵元数和目标源数相等的条件下，RD‑SDF 算法仍能成功定位。

仿真2探究信噪比变化对本文RD‑SDF 算法、文献[21]中传统SDF 算法、文献[23]中Capon 算法和传统二步定位算法定位性能的影响。仿真过程中，采样快拍数K=100，阵元数M=6，信噪比从-5 dB 以 5 dB 间隔步进至30 dB。从图4 可以看出，所提RD‑SDF 算法性能始终优于传统SDF 算法、Capon 算法和传统二步定位算法。

仿真3探究快拍数变化对本文RD‑SDF 算法、文献[21]中传统SDF 算法、文献[23]中Capon 算法和传统二步定位算法定位性能的影响。仿真过程中，阵元数M=6，信噪比SNR=10 dB，快拍数从50 以间隔50 步进至300。图5仿真结果显示，快拍数增加可以提升算法的估计性能，该信噪比下所提算法的性能始终保持最优。

图2 仿真场景示意图Fig.2 Schematic diagram of simulation scene

图3 所提算法估计性能Fig.3 Estimation performance of proposed al‑gorithm

图4 所提算法与现有算法性能对比(改变信噪比)Fig.4 Performance comparison (change SNR)

图5 所提算法与现有算法性能对比(改变快拍数)Fig.5 Performance comparison (change num‑ber of snapshots)

仿真4探究阵元数变化对本文RD‑SDF 算法、文献[21]中传统SDF 算法、文献[23]中Capon 算法和传统二步定位算法性能的影响。仿真实验中，阵元数M分别为3、5、7 和9，采样快拍数K=100，SNR=5 dB。图6 仿真结果显示，当阵元数为3(M=Q)时，传统二步定位算法和传统SDF 算法已经失效，而所提RD‑SDF 算法仍能完成定位，可见本文RD‑SDF 算法具有更大的空间自由度。

仿真5比较算法的计算时间。假设快拍数K=100，信噪比SNR=20 dB，阵元数M=6。从表1 中可以看出，降维后算法的计算时间明显减小，可见所提算法可以有效降低算法复杂度，使算法更具实用性。

图6 所提算法与现有算法性能对比(改变阵元数)Fig.6 Performance comparison (change number of ar‑ray elements)

表1 算法计算时间对比Table 1 Comparison of calculation time between al‑gorithms

5 结束语

针对现代通信系统中常用的非圆信号类型，本文在构建算法模型时结合非圆信号的特征来扩展空间信息，以获得增大的虚拟阵列孔径，与更多的可识别信源数。但由于非圆相位导致的高维搜索大大增加了算法求解时的复杂度，于是本文引入降维思想并结合子空间数据融合的思想，提出了RD‑SDF算法。复杂度分析和计算时间对比结果表明，引入降维思想去除非圆相位搜索维度后，算法复杂度显著降低，但估计精度未受到影响。实验仿真结果表明，在阵元数和目标源数相等的条件下传统SDF 算法和二步定位算法已经失效，而所提RD‑SDF 算法仍能完成目标定位，可见本文算法具有更高的空间自由度；此外，本文RD‑SDF 算法的定位性能要优于传统SDF 算法、Capon 算法和二步定位算法。