多载波雷达系统的信息量及克拉美罗界

徐大专，陈 月，陈越帅，许生凯，罗 浩

（南京航空航天大学电子信息工程学院，南京，211106）

引 言

近年来，在雷达中使用多载波信号引起了人们极大的兴趣[1]。多载波雷达信号可以看作是量化了的频域信号，合成大带宽获得高距离分辨率，且子载波形式适于采用多通道结构获得窄带处理的优势，符合了现代雷达多频段化的趋势[2]。Prasad 提出了多载波雷达系统框架，发现多载波雷达系统具有良好的抗噪声、抗干扰和探测能力[3]。

正交频分复用技术(Orthogonal frequency division multiplexing,OFDM)是一种受到广泛关注的多载波调制方式，具有较强的抗衰落和抗干扰能力、较高的频谱利用率以及易于系统实现等优点[4]。目前，OFDM 技术逐渐引入到雷达系统中。雷达系统对发射波形有特殊要求，Zadoff‑Chu 序列具有恒包络特性和良好的自相关特性，因此，采用 Zadoff‑Chu 序列 OFDM 信号（Orthogonal frequency division multi‑plexing‑Zadoff‑ChuOFDM‑ZC）是 非 常 理 想 的 发 送 波 形[5]。 使 用 循 环 前 缀 Zadoff‑Chu 序 列 的 MI‑MO‑OFDM 雷达可以实现对子载波的无IRCI 重建[6]。

怎样将信息论的思想和方法运用于雷达探测系统，国内外学术界进行了有益的探索。早在香农信息论[7]创立不久，Woodward 和Davies 即开展雷达探测系统中目标的距离互信息问题的研究[8‑10]。他们采用逆概率原理，给出了单目标场景下距离信息的定义，并在高信噪比条件下得到了目标的距离信息的解析表达式。他们只研究了目标幅度为常数的情况，也就是说，只研究了雷达探测系统中目标的距离信息问题，而没有涉及目标的幅度信息问题。

Bell 的开创性论文中将互信息测度用于雷达波形设计[11‑12]。Bell 将雷达信号的目标散射过程等效于一个多径信道，那么，在高斯过程假设条件下，接收信号与目标冲激响应之间的互信息就是信道容量。这样，波形设计问题对应于信道容量在约束条件下的优化问题。因此，最佳波形设计对应于信道容量最大化时的功率注水解。Bell 的方法用目标冲激响应刻画雷达目标散射信道，其模型并不区别不同的目标，也不涉及目标的距离。也就是说，Bell 的工作只研究了雷达探测系统中的幅度信息问题，而没有涉及雷达探测系统中的距离信息问题。文献[13]中首次同时研究了雷达探测的距离信息问题和幅相信息问题，然而针对的是单载波雷达系统。

本文针对多载波雷达系统，运用香农信息理论的思想和方法建立了一个信息理论模型，同时研究目标的距离信息问题以及幅相信息问题。假设在复加性高斯白噪声（Complex additive white gaussian noise,CAWGN）信道中，采用Zadoff‑Chu 序列多载波信号，单目标的距离在探测区间内服从均匀分布，目标的模型分为常散射系数和复高斯分布两种情形，这两种假设情形基于Woodword 的研究[8]。以此为前提，本文推导了目标的概率密度分布函数，距离信息和幅相信息，仿真验证了它们与信噪比的关系，给出了高信噪比条件下无偏估计量的克拉美罗界以及中低信噪比下信息量的理论界。

本文研究表明，目标的信息量和均方误差一样，可以作为雷达系统的另一种性能测度。以距离信息为例，雷达系统每获得1 比特距离信息就意味着目标的探测范围缩小了一半。随着距离信息量的增加，I比特信息量意味着系统的探测精度为2-I。事实上，在中低信噪比环境下，目标可能位于一些不相邻的区域，目标估计的误差并不完全服从高斯分布，因此，在严格意义上，这时用均方误差作为估计精度的性能指标并不准确。本文以比特为单位来衡量雷达系统的性能，为观察雷达系统提供一个新的角度。

1 多载波雷达系统模型

雷达天线发射信号并接收经过目标反射的回波信号，以此来获取目标的探测信息，距离信息反映目标与接收端的距离，与时延有关。幅相信息反映目标的散射系数和相位分布。假设发射信号由N个子载波组成，带宽是BHz，令F=[F0,F1,…,FN-1]T表示通过子载波传输的复数序列，并且这里Fk选用Zadoff‑Chu 序列，ZC 序列具有非常好的自相关性，且具有恒包络特性，是目前优先选择的多载波雷达信号波形。给每个子载波加上循环前缀(Cyclic prefix,CP)后，作为发射波形发送出去。那么，多载波时域发送信号为

式中：s(t)为基带信号，发送信号可以表示为载波为fc，初相为φ0。信号长度为T，Δf=B/N=1/T是子载波间隔。[-T/2-TCP,-T/2]是在离散时域中对应于CP 的保护间隔的持续时间（为了方便表述，这里用了负号），其长度TCP取T，T是不包括CP 的多载波信号的长度，也就是[-T/2-TCP,-T/2]是[-T/2,T/2]的重复，如图1 所示。

图1 加循环前缀的多载波信号结构Fig.1 Multi‑carrier signal structure with cyclic prefix

雷达探测的距离可以用时延表示，假定探测范围是[-D2,D2)，那么对应的时延范围是[-T2,T2)，时延间隔是Δ，这里T= 2D v，v表示信号传播速度。α表示目标的散射系数，d表示目标和接收端的距离，目标的时延τ可以表示为τ= 2d v。将接收端收到的回波信号下变频到基带，并通过带宽为B/2 的低通滤波器，则接收到的窄带信号可表示为

令y=αejφ，φ=-2πfcτ+φ0，w(t)表示复高斯白噪声，实部和虚部均服从N(0,N02 )分布，N02是噪声功率。用B速率对接收信号z(t)进行采样，令t=n/B，得到采样序列为

式中n=-N2,…,N2 -1。通过分析，可以将N=TB表示归一化探测区间，也称为时间带宽积（Time bandwidth product,TBP）。令x=τB表示目标的归一化时延，x∈ [-N/2,N/2)，因此，用归一化时延表示的离散化采样信号为

接收信号z(t)能够完全由N点离散序列z(n)重建，且w(n)的采样值之间相互独立。图2 表示接收信号和参考信号的互相关信号的连续波形和离散波形，假设目标位于区间中间，后面主要分析在归一化观测区间的结果。

图2 3 种探测区间与互相关信号波形Fig.2 Three detection intervals and cross‑correlation signal waveform

本文定义回波信号中有用信号的平均功率和噪声功率之比为信噪比，用ρ2表示，SNR=20log(ρ2)，由于所以

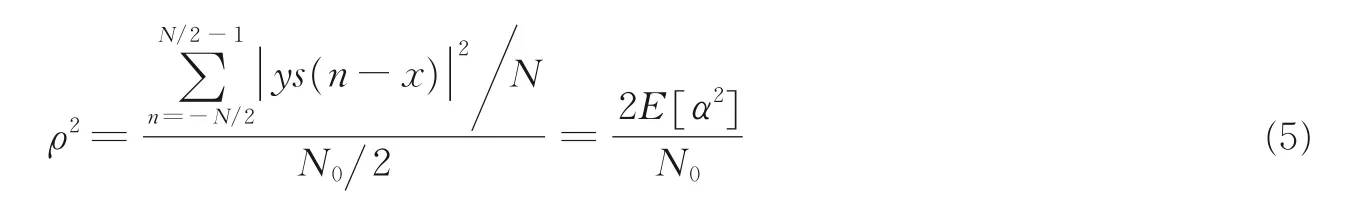
2 探测目标距离信息和幅相信息的统一定义及描述方法

为了更好地表达和分析信号之间的关系，将式（4）写成矢量形式

式中：Z=[z-N2,…,zN2-1]T表示采样信号矢量，U=[u-N2,…,uN2-1]T表示信号矢量，u-N/2=s(-N/2-x)，W=[w-N2,…,wN2-1]T表示噪声矢量。另外，X表示距离参数，Y表示幅相参数，进一步，A表示幅度参数，Φ表示相位参数。雷达探测的目的是从Z中估计X和Y。互信息I(Z;X,Y)表示能够从采样序列Z中获得关于X和Y的信息量。根据互信息的定义和等式，有

式中I(Z,X)表示目标的距离信息，I(Z,Y|X)表示在距离信息X条件下目标的幅相信息。本文假设了目标的散射系数α为常数和目标为复高斯分布两种情形，在常散射系数情况下幅相信息可以简化为相位信息I(Z,Φ|X)。从式（7）中可以发现幅相信息依赖于距离信息，因此雷达系统探测需要分两步进行，首先探测距离信息，然后探测幅相信息。

在雷达探测之前，对目标的距离信息一无所知，也就是目标在探测区间内呈均匀分布。因此，距离参数X的先验概率为p(x) =1/N。由于当载波非常高时，时延微小的的变化都会导致相位很大的变化，所以这里可以假定φ在[0,2π]内均匀分布，也就是φ的先验概率为p(φ) =1/2π。已知W是复高斯白噪声，它的先验概率密度为

根据高斯估计模型，可以写成w(n) =z(n) -y0s(n-x0)，那么，在X，A和Φ条件下Z的N维高斯概率密度函数为

首先来分析目标的距离信息。运用概率公式p(z,x,φ|α) =p(x)p(φ)p(z|x,φ,α)，并对式(10)进行分解，可以得到在给定Α的条件下，Z、X和Φ的联合概率密度为

式中R(⋅)表示取复数的实部。根据概率论的定义，可以得到Z和X的联合概率密度为

令

则

这里I0(⋅)表示第1 类零阶修正贝塞尔函数，式（12）可以写成

利用贝叶斯公式，可以得出目标归一化距离X的概率密度函数为

根据互信息的定义，可以计算单目标探测的距离信息为

考虑目标的幅相信息，由上述推导，同样可以得到Z和X条件下Y的概率密度为

根据条件互信息恒等式，可以得到X条件下的雷达探测系统的幅相信息为

式中H(Y|Z,X)表示在Z和X条件下Y的熵，H(Y|X)是Y的先验信息。距离信息和幅相信息共同构成了雷达探测的互信息I(Z;X,Y)。

3 目标的距离信息

3.1 目标散射系数为常数的距离信息及克拉美罗界

当目标的散射系数为常数Α时，p(α) =Αδ(x-x0)，此时的信噪比为ρ2= 2A2N0，由式（16）得到

代入式（17）可以计算距离信息。

克拉美罗界(Cramer‑Rao bound，CRB)是无偏估计量所能达到的最小均方误差。在高信噪比条件下，归一化时延均方误差的CRB[14]为

式中β是信号的均方根带宽，设信号s(t)的傅里叶变换为S(jω)，由文献[14]中的定义，可以得到

E是接收信号的能量

因此

在高信噪比条件下，目标距离估计的概率密度分布近似为高斯分布，因此可以用高斯分布的微分熵公式来计算H(X|Z)，则有

后面的数值计算表明，在高信噪比条件下，距离信息量以式（25）的结果为渐进上界，这一结论表明，信息理论界与CRB 一致。在高信噪比条件下，最大似然估计的方差逼近CRB，可以用CRB 作为理论界，而实际的雷达系统通常工作于中等信噪比环境下，CRB 不再适合用作理论界。本文给出的距离信息量适用各种信噪比环境，因此，为实际雷达系统的性能提供了理论上界，具有重要的理论指导意义。

3.2 目标模型为复高斯分布的距离信息

当目标服从复高斯分布时，y=αejφ=yreal+iyimg，它的实部yreal和虚部yimg都服从N～(0,σy2)，此时相位φ仍服从均匀分布，而散射系数α服从瑞利分布，其概率分布为

式中:α>0，α的均值为σyπ 2，方差为(2- π 2)σy2。代入式（16）和式（17）可得到目标为复高斯分布时的距离信息。

4 目标的幅相信息

4.1 目标散射系数为常数的幅相信息

当目标的散射系数为常数时，幅度信息已经确定，幅相信息I(Z,Y|X)等效于相位信息I(Z,Φ|X)。通过前面的分析已经得到了目标的距离信息X，这里用X的后验分布来求相位信息。由式（18）可得Z和X条件下Φ的概率密度函数为

根据式（14），对式（27）进行化简得到

根据式（19），可以得到X条件下的雷达探测系统的相位信息为

4.2 目标模型为复高斯分布的幅相信息

通过前面的分析，已经得到了当目标的散射系数服从瑞利分布时的距离信息，此时距离参数X已知，则U(X)矩阵是一个常数矩阵，而Y和W都是独立的高斯矢量，由式（7）可知Z也是一个高斯矢量。因此可以得到Z的协方差矩阵为

当X=x时，由多维相干高斯信源熵的公式，可以得到Z的熵为

并且

因此，在已知条件X=x时，幅相信息为

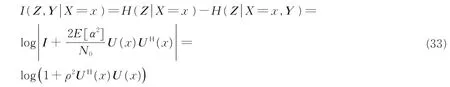
此外，对于x∈[-TB/2,TB/2)，考虑到观测区间的长度远大于U(x)的能量区域，当N足够大的时候，有于是I(Z,Y|X=x) =log(1+Nρ2)。可以发现，幅相信息只与信噪比有关，而与距离信息无关。因此，目标服从复高斯分布时，多载波雷达探测系统的幅相信息为

该幅相信息与香农信道容量的公式相似，这表明，香农信道容量本质上与幅相信息有关，它们之间的关系值得进一步研究。

5 数值仿真结果与分析

本节给出了所有的数值仿真结果与分析，仿真参数的设定为，在多载波雷达系统中，目标距离归一化时延x0=0，时延间隔Δ=0.01，常散射系数α=1，复高斯分布下瑞利分布散射系数的均值为1，单位带宽，CWAGN 信道。时间带宽积的探测区间为[-TB/2,TB/2)。

5.1 概率密度分布

图3 给出了N=16，目标的散射系数为常数时，不同信噪比下目标距离的概率密度分布图，由式（20）得到。为了便于观察，这里只截取了部分区间。可以看出，概率密度分布呈现为高斯分布，其均值为x0，方差为σ2= 4()I-logTB2πe。根据高斯分布的3σ原则，目标归一化距离的搜索区间基本确定。接收端每获得一个比特的信息量，等效σ缩小一半，即搜索区间缩小了一半，若雷达系统能获得I比特的距离信息量，意味着该系统的距离测量精度为2-I。因此，获得的信息量越多，概率密度分布越尖锐，得到的目标距离越精确。

图3 目标距离估计值的概率密度分布Fig.3 Probability density distribution of target distance

5.2 距离信息量

图4 给出了理论模型、最大似然估计以及克拉美罗界的距离信息量与信噪比的关系曲线。从图4 中可以看出，当TB固定时，随着信噪比的增加，距离信息量的变化规律大致可以分为两个重要的阶段，第一阶段称为“目标搜索阶段”，此时距离信息量随信噪比增长的斜率较大，当信息量达到logTB时，目标搜索区间缩小至观测区间的1TB，即系统分辨率达到1B。第二阶段称为“目标定位阶段”，即在高信噪比区域，此时距离信息量增长的斜率恒定，趋近于克拉美罗界，随信息量增加，目标距离的估计范围继续缩小，从而突破了1B的限制。理论模型的距离信息量可以作为雷达系统距离信息量的理论界。

图5 给出了N=64 时，两种目标模型下距离信息量与信噪比的关系曲线，从图5 中可以看出，距离信息量随着信噪比的增加而增加，并且目标复高斯分布模型获得的距离信息量高于常散射系数模型，这是因为在检测过程中目标复高斯分布模型带来的不确定性比常数更大。

图4 距离信息量的比较Fig.4 Comparison of distance information

图5 不同目标模型下的距离信息量Fig.5 Distance information under different target models

5.3 均方误差

图6 比较了3 种归一化时延的均方误差，分别是理论模型、最大似然估计和克拉美罗界。理论模型曲线是对信息量求其等效的高斯分布的方差得到的。可以看出，方差随着信噪比增大而减小。在高信噪比区域，克拉美罗界是理论模型方差的渐进下界，验证了理论分析的正确性。

5.4 幅相信息量

图7 中给出了目标常散射系数模型下的相位信息量和复高斯分布模型下的幅相信息量与信噪比的关系，可以看出相位信息和幅相信息都随信噪比的升高而升高，且在高信噪比条件下都与信噪比成线性关系，并且目标复高斯分布模型获得的幅相信息量高于常散射系数模型获得的相位信息量。

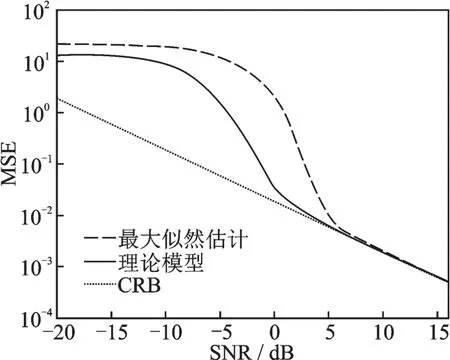
图6 均方误差的比较Fig.6 Comparison of the mean square error

图7 幅相信息量与信噪比的关系Fig.7 Relationship between amplitude‑phase information and SNR

6 结束语

本文基于香农信息理论，建立了多载波雷达系统的信息理论模型。研究表明，目标的信息量和均方误差一样，可以作为雷达系统的另一种性能测度。以距离信息为例，雷达系统每获得1 比特距离信息就意味着目标的探测范围缩小了一半。随着距离信息量的增加，I比特信息量意味着系统的探测精度为2-I。理论分析与数值仿真结果表明，在高信噪比条件下，Cramer‑Rao 界就是距离信息量的渐近上界。实际雷达系统通常工作于中等信噪比环境，目标的距离信息量可作为最大似然估计的性能上界，为实际系统的性能提供了比较的依据。此外，信噪比和TB 是雷达系统探测性能的两个重要影响因素，可以根据信噪比和TB 预估雷达系统探测性能，也可以依据所需信息量来判断信噪比的下界，这可以指导在实际中更有效地对目标进行探测，也可以指导雷达系统设计。本文的分析基于CAWGN 信道，针对单目标探测的情形，且不考虑信号衰减的情况，但实际的雷达探测场景更加复杂，因此需要将本文的研究结论进行推广，如衰落回波信号，目标之间存在干扰的广义多目标探测情景等，这些问题都是值得进一步深入研究的重点。