理想毫米波信道条件下低复杂度的混合波束成形

林 振，李 莉，魏 爽，吴静芳

（上海师范大学信息与机电工程学院，上海，201418）

引 言

多输入多输出(Multiple input multiple output, MIMO)通信系统是第5 代移动通信技术(Fifth genera‑tion mobile networks,5G)中极其关键的技术，但是无线通信系统频谱资源稀缺成为其发展的瓶颈，然而毫米波频段频谱资源丰富[1]，因此MIMO 技术可以在毫米波频段得到很大的利用[2]，MIMO 技术在毫米波频段中还可以实现大量小尺寸天线的集成。但是毫米波频段中有着较为严重的路径损耗，所以实现MIMO 技术在毫米波频段的优越性需要高效的波束成形技术来补偿路径损耗，改善传输质量[3]。由于全数字的波束成形方案相对于大规模MIMO 通信系统而言过于复杂，而模拟波束成形虽然节省了成本，但是每条射频链路只能支持单流数据传输，限制了大规模MIMO 通信系统的优势，系统性能大大降低，因此混合波束成形是解决这一问题的关键[4]。

针对单用户MIMO 通信系统的混合波束成形技术，文献[5]假设已经知道信道状态信息(Channel state information, CSI)，首先研究了射频链路数为数据流数两倍时的混合波束成形，然后又研究了射频链路数小于数据流数两倍时两种特殊通信场景下的混合波束成形：一是基站端和用户端均为大规模天线阵列的点对点MIMO 通信场景；另一是基站端为大规模天线阵列，多个用户均是单天线的多输入单输出(Multiple‑input single‑output，MISO)下行链路通信场景。文献[6]首先提出将非凸约束的总可实现速率的优化问题分解为多个简单的可实现子速率问题，每个问题仅考虑一个子天线阵列，最后利用串行干扰消除(Successive interference cancelation, SIC)的思想，提出了一种基于SIC 的混合波束成形算法。文献[7]针对完全连接结构和部分连接结构的混合波束成形，提出了交替最小化算法(Alternating minimization, AltMin)，特别针对完全连接结构的混合波束成形，提出了基于多重优化的AltMin 算法，该算法不需要预定的码本，直接在单位模约束的情况下进行模拟波束成形矩阵的求解；其次对于部分连接结构的混合波束成形，提出了基于半定松弛的AltMin 算法，该算法在每次迭代中为模拟和数字波束成形的子问题提供最优解，有效地设计了混合波束成形器。

以上文献均是针对点对点的MIMO 通信场景或者是多个用户均是单天线的MISO 场景，但是在实际应用系统中多是一个基站同时服务多用户，且基站端和用户端均是多天线的场景，所以一些论文将波束成形的设计问题扩展到多用户MIMO(MU‑MIMO)通信系统中。文献[8]针对多用户的MIMO 下行链路场景，采用了一种接近传统块对角化(Block diagonalization,BD)方案的混合块对角化(Hybrid block diagonalization, Hy‑BD)方案，并在等效信道的基础上设计数字波束成形器，但是其在设计用户端模拟波束成形矩阵时采用的是在码本中直接选择波束矢量的方法，这种方法可能会造成系统的性能不佳。文献[9]将文献[10]中提出的矩阵的广义低秩近似(Generalized low rank approximation of matrices,GLRAM)算法应用到模拟波束成形矩阵迭代求解中，利用BD 算法求解数字波束成形矩阵，其中在迭代求解模拟波束成形矩阵过程中每一次迭代均进行奇异值分解(Singular value decomposition, SVD)运算，使得此种算法的复杂度较高。文献[11]中使用的是部分连接的混合波束成形结构，在模拟波束成形求解中使用了SVD 分解，但是其采用的部分连接的混合波束成形结构会造成系统性能的下降。

本文针对上述文献算法的问题，提出了一种低复杂度的全连接的混合波束成形方案，将波束成形设计问题转化为两步进行:（1）直接利用奇异值分解方法来分别设计基站端和用户端的模拟波束成形矩阵，计算模拟波束成形的乘法次数较少;（2）采用传统的性能较好的BD 算法设计数字波束成形矩阵来消除用户间的干扰，在复杂度较低的同时实现了较高的系统频谱效率。

1 系统模型

1.1 毫米波MIMO 信道模型

本文的毫米波MIMO 信道采用成簇信道(Clustered channel)模型[12]，对于第k个用户，毫米波MIMO信道矩阵为

式中：Nc是散射簇数，Np是一个散射簇中的路径数；αil是第i个散射簇中第l个路径的复增益，服从复数正态分布 CN(0,1)；与分别代表第k个用户第i个散射簇中第l个路径的离开角和到达角，服从[0,2π]上的均匀分布分别是基站端和用户端的天线阵列矢量，分别为

式中：j 为虚数单位，d为相邻阵元之间的间隔，λ为窄带信号的波长，一般d=λ/2。

1.2 混合波束成形的信号模型

假设在多用户的MIMO 通信系统中，一个小区的基站配有Nt根天线和个射频链路，同时为小区内的K个用户提供通信服务，每个用户配置Nr根天线和个射频链路，Ns表示发送给一个用户的数据矢量的长度，如图1 所示。为保证通信的有效性，需要基站端和用户端射频链路的个数分别满足。

图1 毫米波多用户MIMO 系统Fig.1 Millimeter wave multi-user MIMO system

图1 中s∈ CKNs×1为K个用户总的信号向量，可以表示为为发送给第k个用户的数据矢量，s满足代表平均传输功率，nk为一个Nr×1 的加性复高斯噪声向量的数字波束成形矩阵，FBB同时调制信号的幅度和相位，以便克服信道干扰和其他用户的干扰。的模拟波束成形矩阵，而FRF只改变信号的相位信息，故矩阵上每个元素满足其作用是将信号定向发送。Hk∈CNr×Nt是基站到第k个用户的毫米波信道矩阵，则系统下行链路中第k个用户天线处的接收信号yk为

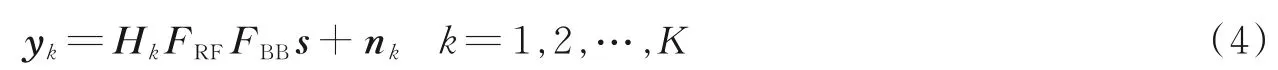
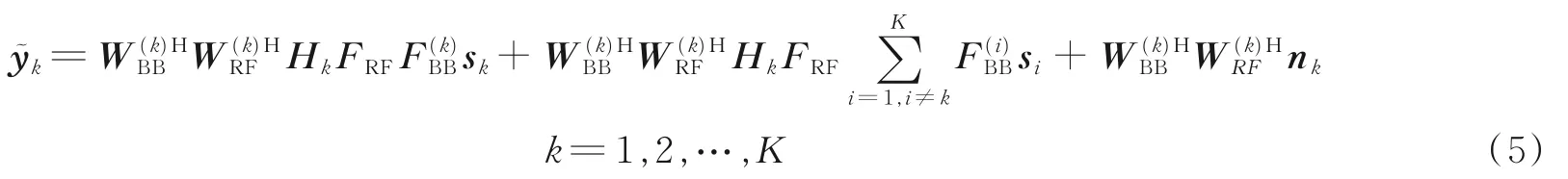
式中等式右边第1 项是第k个用户期望信号，而第2 项是其他用户的干扰，第3 项是噪声项。

2 低复杂度混合波束成形方案及算法复杂度分析

2.1 混合波束成形问题

1.2 节中给出的用户端和基站端均是混合波束成形结构的MU‑MIMO 系统的总频谱效率可以写成[13]

显然，MU‑MIMO 系统的总频谱效率R最大化问题，与基站端和用户端的模拟波束成形矩阵和数字波束成形矩阵直接相关，可等效为混合波束成形问题。因此，混合波束成形问题可以建模为优化问题，如式(7a—7c)所示。

在式(7b)，(7c)的约束条件下，求解式(7a)所述的最大化问题是一个非凸问题[11]，而求解非凸问题是一个非常困难的事情。为了简化此问题，可将此问题分为两个阶段进行，第1 阶段进行模拟波束成形矩阵的求解；第2 阶段进行数字波束成形矩阵的求解[8‑9]。但是文献[8]在设计用户端模拟波束成形矩阵时采用的是在码本中直接选择波束矢量的方法，这可能会造成系统的总频谱效率的下降；而文献[9]用GLRAM 算法迭代求解模拟波束成形矩阵之后，利用BD 算法求解数字波束成形矩阵，存在算法的复杂度较高问题。针对上述文献中的问题，本文提出一种新的两个阶段进行的混合波束成形方案。

2.2 低复杂度混合波束成形方案

针对式(7a—7c)中给出的混合波束成形问题，本文提出的改进的两个阶段混合波束成形问题求解方案具体是：首先利用SVD 分解求解模拟波束成形部分，在求出用户端模拟波束成形矩阵的基础上去求解基站端的模拟波束成形矩阵；然后针对数字波束成形矩阵进行求解，有迫零(Zero forcing, ZF)算法和BD 算方法可选，虽然ZF 算法比较简单，但是其放大了系统噪声，性能较差，相比之下虽然BD 算法使用了SVD 增加了复杂度，但是其性能更加优异。由于本文还同时要考虑系统性能因素，所以本文选择BD 算法进行数字波束成形的求解，具体算法步骤如下。

步骤1模拟波束成形矩阵求解

（1）求解第k个用户的模拟波束成形矩阵

本文首先将第k个用户的毫米波信道矩阵Hk进行奇异值分解为

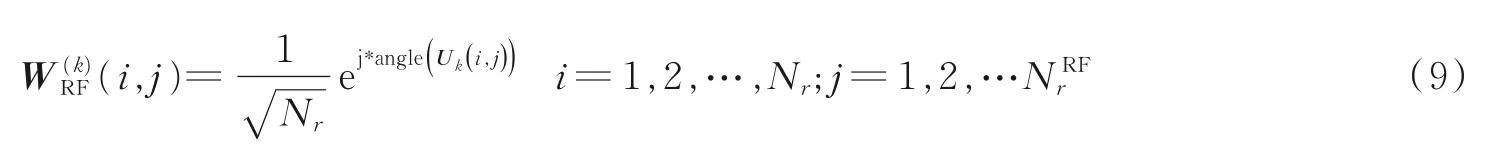
（2）在求解出所有用户的模拟波束成形矩阵的基础上求解基站端的模拟波束成形矩阵FRF。

定义H'为

对矩阵H'进行奇异值分解得

然后令FRF矩阵中每个元素的相位等于右奇异矩阵V'中对应位置元素的相位，令FRF矩阵中每个元素的模值为，则

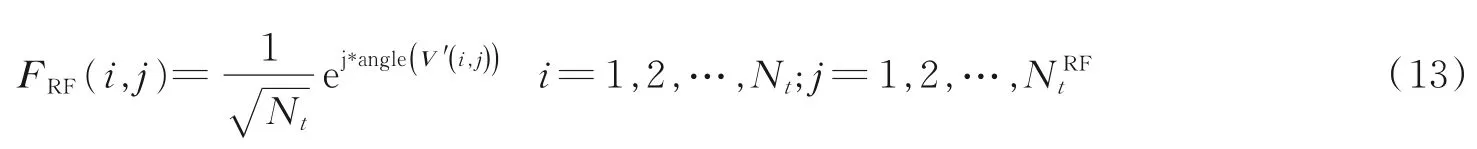
步骤2数字波束成形矩阵求解

（3）等效第k个用户的基带信道为

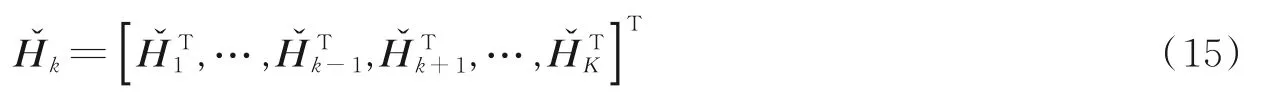
（5）求解基站端的针对第k个用户的数字波束成形矩阵和第k个用户的数字波束成形矩阵。

具体算法的流程框图如图2 所示，由图2 可以看出本文在求解用户端和基站端模拟波束成形矩阵时分别只进行了一次SVD 分解，比文献[9]中多次迭代使用SVD 求模拟波束成形矩阵的方法复杂度降低；也不像文献[8]那样直接在码本中进行用户端波束成形矩阵矢量的选择，虽然降低了复杂度，但是以性能下降为代价的。

图2 低复杂度混合波束成形算法流程框图Fig.2 Flow chart of low-complexity hybrid beamforming algorithm

3 实验仿真分析与算法复杂度

在第2.2 节中已经给出本文算法的步骤，为了验证本文所提低复杂度混合波束成形算法的性能，在毫米波多用户MIMO 通信系统场景下进行几种算法的总频谱效率的仿真分析，表1 为仿真参数设置。

首先进行几种算法计算复杂度的分析，本文算法创新在求解模拟波束成形矩阵处，因为计算乘法耗时比计算加法耗时多，所以此处主要以求解模拟波束成形过程中进行乘法的次数来衡量计算的复杂度，假设n表示GLRAM 算法进行迭代的次数，计算复杂度如表2 所示。

图3 是当基站天线数变化，而且GLRAM 算法的循环次数n变化时根据表2 中复杂度公式得出的复杂度仿真图，可以看出本文的算法复杂度比Hy‑BD 算法的复杂度要略高，但是比n为4 时的GLRAM 算法要低，而在实际仿真中，GLRAM 算法的n一般都在10 左右。

表1 仿真参数Table 1 Simulation parameters

表2 算法复杂度分析Table 2 Algorithm complexity analysis

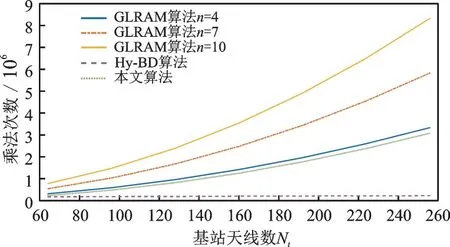
图3 几种算法的算法复杂度仿真图Fig.3 Algorithm complexity simulation of several algorithms

图4 是几种算法总频谱效率的对比，由图4 可以看出，随着发送信号信噪比的增加，系统的总频谱效率逐渐上升，这是由于发送信号信噪比的增大导致接收信号的功率也随之增大，所以造成了系统总频谱效率的增大。在图4 中可以看出，在本文所提算法下，系统的总频谱效率略高于GLRAM 算法，但是在此仿真条件下，本文算法的复杂度却只有GLRAM 算法的1/3。同时本文所提算法的系统的总频谱效率远远高于Hy‑BD 算法，这和Hy‑BD 算法在设计用户端模拟波束成形矩阵时采用是在码本中直接选择波束矢量的方法有关系，这也是Hy‑BD 算法复杂度小的必然代价。传统的BD 算法即数字波束成形方法，GLRAM 算法和本文算法均优于传统的BD 算法，实现了在少量射频链路的情况下，达到了传统数字波束成形的性能。

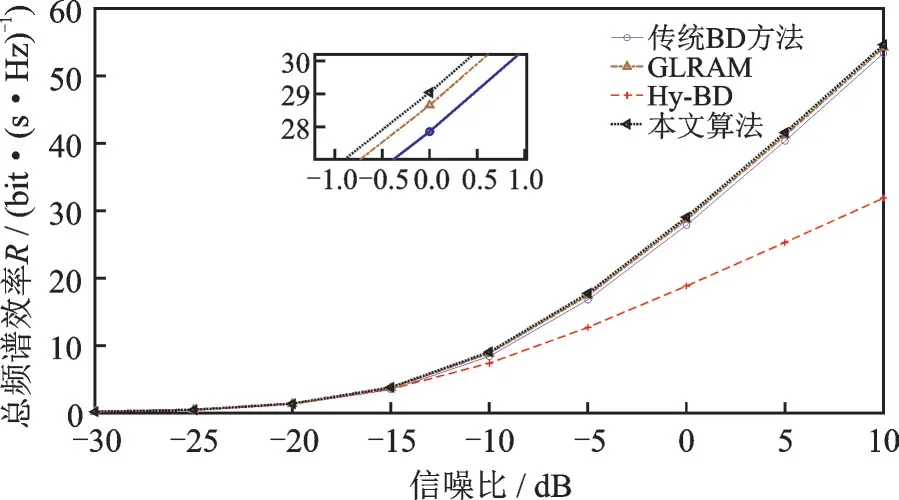
图4 几种算法的总频谱效率对比Fig.4 Comparison of total spectrum efficiency of several algorithms

图5 是当发送信号的信噪比分别固定在0 dB 和10 dB 时，而基站天线数从64 递增到512 时总频谱效率的变化情况，由图5 可以看出，随着基站天线数量的增大，系统的总频谱效率是逐渐上升的，这是因为MIMO 通信系统在相同的时频资源条件下，增加天线数量，即可提升系统容量，即提升系统的频谱效率。在图5 可以看出，本文所提算法下的系统总频谱效率略优于GLRAM 算法，同时两种算法的系统总频谱效率都要比传统的BD 算法的差，这是因为传统BD 算法是要求一根天线配备一条射频链路，所以性能优异，但是随着天线数量的增加，所需的射频链路数也随之增加，这就造成了高昂的成本。本文算法在配备少量射频链路数的情况下，有着较好的性能，实现了成本和性能的折中。

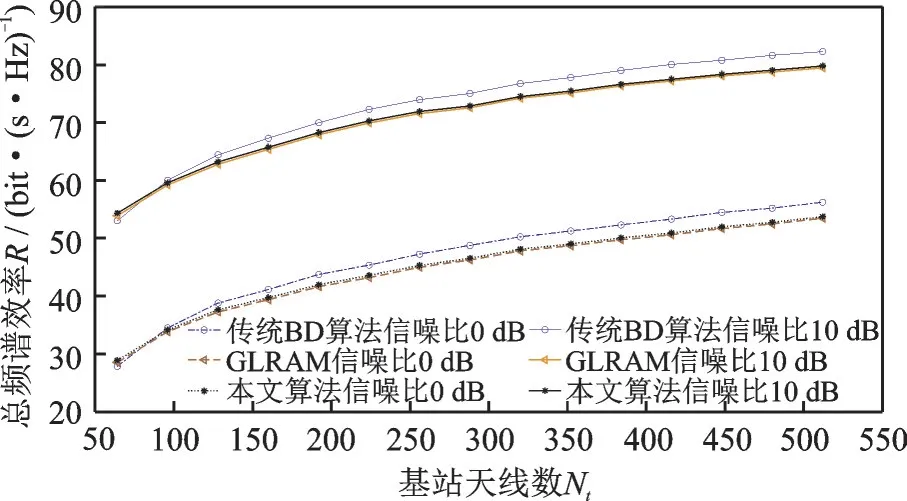
图5 不同信噪比下总频谱效率和基站天线数的关系Fig.5 Relationship between total spectrum efficiency and the number of base station antennas under different SNRs

4 结束语

本文主要研究了在单小区内基站和多用户均是混合波束成形架构的情况下，如何设计波束成形矩阵使多用户MIMO 通信系统的总频谱效率最大化的问题。主要分两步进行:第1 步利用SVD 方法设计模拟波束成形矩阵；第2 步在求得的模拟波束成形矩阵基础上，等效基带信道，并利用传统的BD 算法求解数字波束成形矩阵。由于本文在数字波束成形的求解中用了BD 算法，而未使用复杂度更低的ZF 算法，所以本文低复杂度算法保证性能的同时降低了整体的复杂度。