一种管道中的导波频散计算方法

文立超，张应红，刘文龙，张奥申

(桂林电子科技大学 机电工程学院, 桂林 541004)

基于导波的无损检测方法具有传播速度快、方向性好、应用范围广等特性。但是由于导波具有多模态、易频散的特性，其频率的选择及频散往往会影响检测结果的准确性，因而研究管道中导波的频散关系对于导波检测的应用具有重要意义。

英国帝国理工大学的LOWE等[2-3]研究了充水埋地钢管的频散曲线及衰减特性，并基于解析法开发了频散曲线软件Disperse；SECO[4]在此方法基础上通过MATLAB软件开发了PC disp工具箱，该工具箱可用于分析管状导波的频散及传播情况。北京工业大学的何存富[5]采用矩阵法对立柱埋地部分和未埋地部分的频散特性进行了研究。近年来半解析有限元方法在频散分析方面得到了广泛应用。其中，具有代表性的有:BOCCHINI[6]基于半解析有限元法开发了GUWGUI软件，可用于各种复杂截面的导波频散关系的求解;浙江大学的胡剑虹[7]等对半解析有限元法的求解矩阵规模进行了改进，减少了计算量;海军工程大学的王悦民[8-9]采用有限元的特征频率法求解了管道的频散曲线，该方法建立了三维模型，求解自由度大，需从可视化的角度统计周期数及模态数，进而求得频散关系，但操作繁琐。笔者提出一种基于有限元的模式分析法，通过推导导波传播的波动方程，采用分离变量法得到亥姆霍兹方程，并用有限元法求得特征值解，从理论上证明了模式分析法的可行性。利用COMSOL Multiphysics软件建立了二维管道截面的有限元模型。根据低频下的导波频散关系特点，进一步采用弹性波理论及铁木辛柯梁理论对模式分析方法及半解析有限元法的求解结果进行验证，最后对位移分量进行坐标变换及波结构特征分析。该方法与传统半解析有限元法相比，需要设置模式阶数，在有限元软件中可以方便地得到频散关系，为导波的频散计算分析提供了一种新的思路。

1 理论基础

假定管道材料为各向同性、均匀同质的线弹性体，内外径分别为a,b，不考虑体力及惯性力的影响时，其一般的弹性动力学方程(Navier-stokes方程)如式(1)所示。

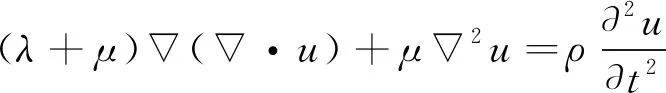
(1)

式中:u为时间谐振位移矢量;ρ为材料密度;λ和μ为材料的拉梅常量。

位移场通过亥姆霍兹分解可表示为标量φ的梯度和矢量H的旋度，即

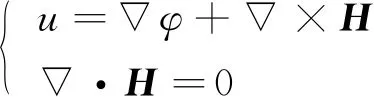
(2)

将式(2)代入式(1)中可得

(3)

若要使式(3)成立，需要满足下列关系式

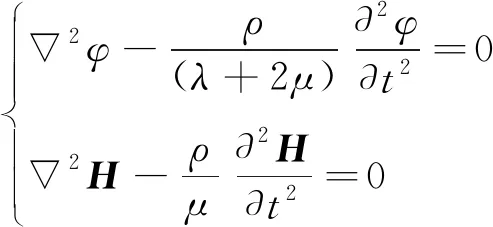
(4)

由式(4)分析可得此方程为两个形式一致的波动方程，而纵波波速cL可表示为

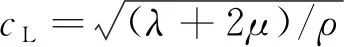
(5)

横波波速cT为

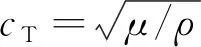
(6)

因此，在波导中不仅存在以纵波传播的伸缩扰动，而且存在以横波传播的切变扰动。模式分析法是对波动方程进行时空分离，并求解模式特征值解的方法。式(4)中由于求解的是同一类型的方程，所以可将φ,H统一记做ψ，cL、cT统一记做c，初始状态下管道内外壁节点的位移及速度为0。往z方向添加入射的简谐波，波的传播函数可以用ψ=U0exp(iωt-ikz)进行描述,其中U0为波的幅值矢量。于是对ψ作变量分离ψ=U(x,y,z)T(t)=U(x,y,z)exp(iωt)，可得到下面两个微分方程式。

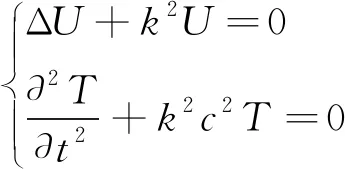
(7)

式中：k为分离常数波数;U为波动位移幅值；t为波在波导里的传播时间；T为仅与t有关的待定函数；x,y,z为空间坐标的笛卡尔坐标系;ω为波传播的角频率。

根据变分原理，亥姆霍兹方程相应的泛函可用下式表示。

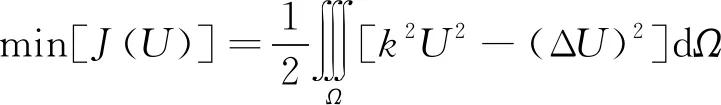
(8)

式中:Ω为求解区域;J(U)为波动位移幅值的能量，min[J(U)]表示最小能量。

将其剖分为四边形网格，设Ni为形函数，记B=Ni。则通过对泛函求极值可导出有限元方程,如式(9)所示。

AU=0

(9)

式中:A为总体刚度矩阵，其表达式如式(10)所述。

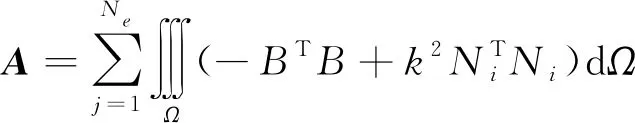
(10)

式中:Ne为网格数。

若给定参数f(波的特征频率)，有k=2πf/c，对式(9)中矩阵A进行特征值求解，可得到一组k，将k代入式(9)，可求出U，即模态特征。

2 频散分析

2.1 频散关系求解

图1 管道二维离散模型

以外径a为30 mm，内径b为25 mm的铝材管道为例，建立几何模型，添加材料为铝，并划分单元网格为四边形的映射网格，管道二维离散模型如图1所示。由于是理想情况下的管道，其不受外力作用，所以设置为自由边界条件。铝主要的材料参数如表1所示(表中E为弹性模量，ν为泊松比)。

表1 铝的材料参数

将建立的几何模型放置在固体力学场中求解，设定求解步骤为模式分析，并取求解模式数为30，选择频率步长为100 Hz，模式搜索基准值为2πf/c，这里根据经验值设定c为330 m·s-1，并以频率作为扫描参数。根据文献[7]，通常导波检测所用的检测频率较常规超声波的频率低，由于管道截面中的导波高阶模态十分复杂，计算会引入较多的复杂模态，且对计算要求较高，因此选定求解频率的最大值为100 kHz，通过求解得到了频率-波数曲线，如图2所示。为了验证文章方法的合理性，将其和半解析有限元方法求解的结果进行了比较。

图2 频率-波数曲线

进一步地，由已求得的频率f及波数可求得相速度cp，其满足关系式

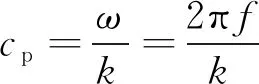
(11)

根据式(11)可得到其相速度频散曲线，如图3所示。

图3 相速度频散曲线

类似地，根据所求的频率波数关系，可知其群速度cg满足以下表达式

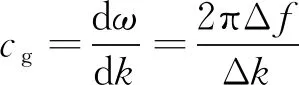
(12)

为求得群速度，可使Δf=1，则需要另计算f′=f+1的波数值，以得到两组k值，求得Δk。所求得的群速度频散曲线如图4所示。

图4 群速度频散曲线

对图2～4进行分析，可以得到以下结论。

(1) 基于有限元的模式分析方法不但与半解析有限元法所得到的结果相吻合，而且求解得到了由结构特征变化衍生出来的环状模态[11-12](两种方法所绘制曲线的未重合部分)，证明了该法的有效性。环状模态是由于模式叠加产生的，在实际检测中应该避免该类模态产生，以降低检测信号的复杂性。

(2) 导波在管中传播存在多模态现象，高频情况下此现象更加突出。在0～100 kHz频段中两种方法所绘制曲线的重合部分，导波模态主要有纵向模态、扭转模态及弯曲模态三类，每一类模态又细分为多种模式。而随着频率的增加，模式数相应增加。

(3) 0～20 kHz的低频段与频率超过20 kHz的频段相比，导波模态较少，且频率和波数之间的关系近似为线性关系。

2.2 频散关系分析

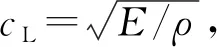
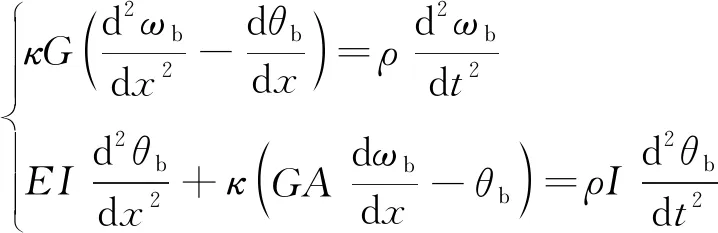
(13)

式中:A为截面面积;I为截面惯性矩;ωb为弯曲位移;θb为转角;κ为剪切系数；G为剪切模量。

根据参考文献[11]可得剪切系数如下式所示。

(14)

式中:m为内外径之比，即b/a。

对式(13)进行傅里叶变换，得到其解。对应的实数域下弯曲波数为

(15)

将ω以及表1中的相关材料参数代入上式即可求得弯曲模态下的理论解 。

综上所述，可得频率为10 010 Hz下的波数理论值，且可通过计算求得与其他两种方法的相对误差，如表2所示。

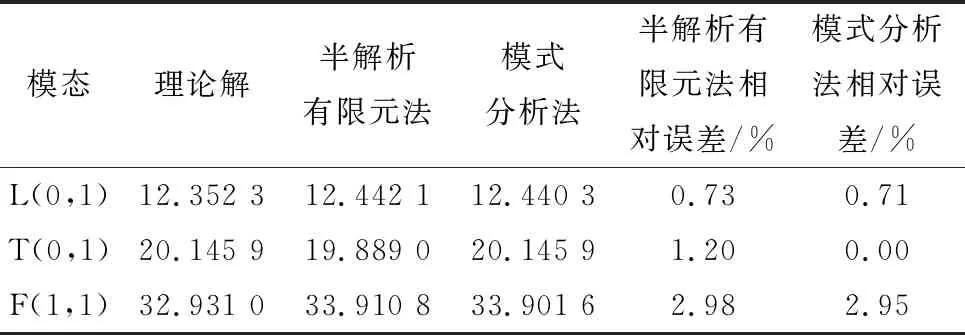
表2 不同方法得到的结果比较

由表2可得到，由理论所求得的波数解与半解析有限元法、模式分析法所求的波数基本一致，均可得到准确解。但是，针对L(0,1)和F(0,1)模态的波数解，模式分析法较半解析有限元法的精度有微弱的提高，而扭转波模态T(0,1)波数的求解精度显著提高，可见模式分析法更适用于扭转模态的求解。综合来看，半解析有限元法与模式分析法所得结果的误差均较小，但是有限元的模式分析方法的精度更高，体现了该方法的优越性。

3 模态特征分析

模态特征可以表征导波在管道中传播的波结构特征，通常选取的模态特征有位移变化、应力变化以及能量变化。由于导波检测中较易获得位移量[14]，所以文章采用位移变化来表征模态特征，以频率为10 010 Hz时的各模态位移特征进行模态特征分析。为使得位移的表示更加合理，将笛卡尔坐标系下的位移变化量转换为柱坐标系下的位移变化量，则各个方向的位移如下式所示。

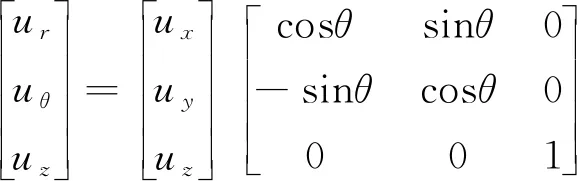
(16)

式中:ux,uy,uz分别为模态在直角坐标系中的x,y,z三个方向上的位移分量；ur,uθ,uz分别为模态在柱坐标系中的径向、切向及轴向上的位移分量；θ为旋转角。

通过上面的转换矩阵，在后处理结果中得到柱坐标下各个分量的位移，并对位移分量进行归一化处理，从而得到各模态下的位移分布，如图5～7所示。

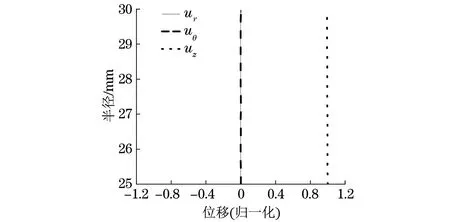
图5 10 010 Hz下L(0,1)模态的各分量位移图

图6 10 010Hz下T(0,1)模态的各分量位移图

图7 10 010 Hz下F(1,1)模态的各分量位移图

由图5可知，L(0,1)模态存在轴向位移，内外壁的位移分布几乎相等，且远大于径向位移。而径向位移和周向位移量接近于0。由图6可看出，对于T(0,1)模态的导波，存在周向位移，且外表面壁的位移比内表面壁的位移更大。而F(1,1)模态在三个分量下均有位移，周向位移和轴向位移都较小，径向位移最大，在管道中的传播比较复杂。

4 结论

采用基于有限元的模式分析法求解管道中导波的频散关系，通过亥姆霍兹方程得到波数和角频率之间的关系式，并采用有限元方法进行了数值计算，利用COMSOL Multiphysics软件建立模型，给定频率参数，模式数及模式搜索基准值求解得到了频散曲线及管道截面上的位移形变结果。与半解析有限元方法的求解结果相比，模式分析法得到了由模式叠加产生的环状模态，说明了该法求解的全面性。同时，参照理论解，模式分析法的精度良好，且更适用于T(0,1)模态的求解。