主成分分析法在脉冲涡流缺陷识别中的应用
2020-12-18陈卫林
张 旻,陈卫林,李 骥
(中国核动力研究设计院,成都 610213)
脉冲涡流检测(Pulsed eddy current,PEC)具有频谱宽、信号穿透能力强等特点,能克服传统涡流检测的趋肤效应,在检测多层金属结构缺陷时具有优异性能,因而被广泛应用于涂层测厚、管道和承压设备腐蚀缺陷的在役检查中[1],已成为现代无损检测技术的重要方法之一。与传统涡流检测采用单一正弦波或多个离散频率连续谐波作为激励源不同,脉冲涡流检测的基本原理是在线圈中通入恒定电流或电压,在一定时间内待测构件中会产生稳定的磁场,当断开输入时,一次磁场的急剧减小会使得待测构件中感应生成涡流,形成二次磁场而影响线圈磁通的变化。此时,电磁场由直接从线圈中耦合出的一次电磁场和构件中感应出的涡流场产生的二次电磁场两部分叠加而成,且后者包含了构件本身的厚度或缺陷等信息,采取合适的方法和检测元件对二次场进行测量,分析测量信号,即可得到待测构件的信息[2]。
脉冲涡流的缺陷识别中,采集的检测信号携带的是待测构件的电磁特性、缺陷、传感器提离等综合信息,通常需要从时域与频域中寻找特征参数对缺陷进行表征。单一特征参数包含的构件信息往往十分有限,且可能存在校准困难或噪声引起的重复性不好等问题[3],无法建立缺陷与脉冲涡流信号特征之间的直接映射关系。因此,需要检测人员联合多个特征参数进行综合分析,来达到准确识别缺陷的目的。目前,在脉冲涡流缺陷识别中常用的时域信号特征参数有峰值幅度、峰值时间、过零时间、主峰面积、衰减时间等[4];常用的频域信号特征参数有峰值频率。典型脉冲涡流信号及其特征参数如图1所示。上述特征参数从不同角度反映了缺陷的特征,为缺陷的准确识别提供了更加丰富的信息,但各特征参数之间相互关联,存在一定的信息冗余[5],增加了检测数据分析量和信息筛选难度,影响了缺陷识别的效率。
信息冗余问题在模式识别、人工智能等领域的研究中备受关注,目前主要采用主成分分析、因子分析、独立分量分析等方法对原始数据进行处理以减少信息冗余。笔者选用主成分分析法对钢板脉冲涡流信号的6个特征参数进行降维处理,构造了一个关键特征并将其输入至Logistic分类器进行缺陷的自动识别,以期有效减少分类器处理的数据量,提高缺陷识别效率。
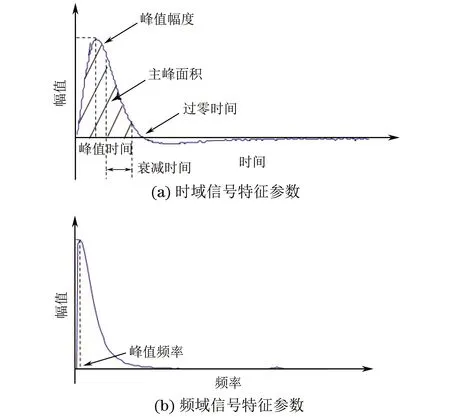
图1 脉冲涡流信号特征参数
1 方法论述
1.1 主成分分析法的原理
主成分分析法主要用于提取数据关键信息,减少信息冗余,其基本原理为:设有p个原始变量x1,x2,…,xp,通过式(1)所示的线性变换将原始变量转化为p个主成分y1,y2,…,yp,具体变换步骤参考文献[6]。
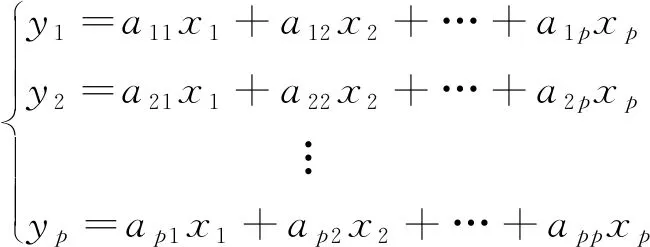
(1)
式中:yi为第i主成分;aij为主成分系数;i,j=1,2,…,p。
主成分满足以下条件:①yi,yj互不相关(i≠j,i,j=1,2,…,p);② 主成分方差Var(y1)>Var(y2)>…>Var(yp),其中Var(y)可由式(2)表示。
(2)
由式(1)可知,主成分包含了原始变量的所有信息;由条件①可知各主成分包含的信息相互独立;由条件②可知各主成分包含的信息量互不相等。各主成分包含的信息常采用以下统计量进行定量描述,即特征值λi,方差贡献率Cri和累计方差贡献率ACrk,如式(3)所示。
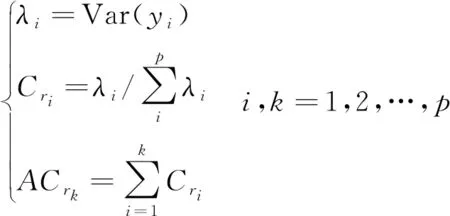
(3)
其中,特征值λi越大,则该主成分的影响力越大,对数据信息的解释能力越强;方差贡献率Cri越大,则该主成分所包含的信息量越大;如果累积贡献率ACrk达到75%以上,则可认为选取的k个主成分能包括数据的绝大部分信息。
1.2 Logistic回归分类原理
Logistic回归模型在二分类识别中应用广泛,假设试验中第i个脉冲涡流检测样本(i=1,2,…,N)为缺陷的概率为Pi,记为:
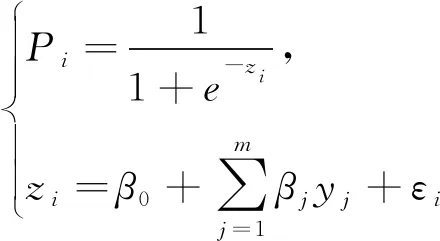
(4)
式中:yj为判定的影响变量;βj为需要估计的判定系数。P的函数呈S型分布,且为递增函数,P∈(0,1)。
由于
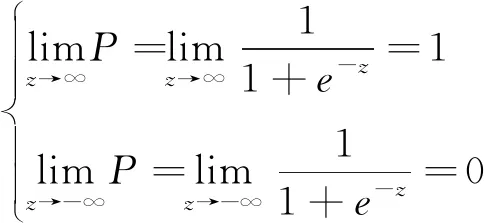
(5)
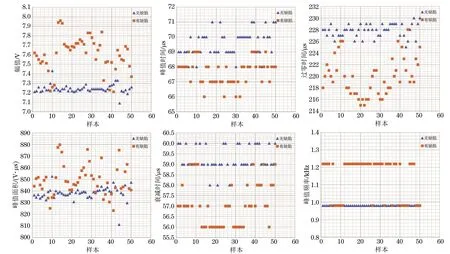
图4 脉冲涡流信号特征分布
对于任意一个脉冲涡流检测样本i而言,若Pi≈0表示出现缺陷的概率很小,可以判定无缺陷;反之,若Pi≈1表示出现缺陷的概率很大,可以判定有缺陷。式(4)中的判断系数可以采用极大似然函数法求解,估计判定系数,上述求解过程可在SPSS软件中直接完成[7]。
2 试验与分析
2.1 脉冲涡流检测试验
针对制作有人工减薄缺陷的不锈钢板进行脉冲涡流检测试验。试验件材料为304不锈钢,设计尺寸为(长×宽×高)300 mm×165 mm×5 mm。在不锈钢板S1面加工有尺寸(直径×深度)为15 mm×2 mm的平底孔,作为人工减薄缺陷,如图2所示。
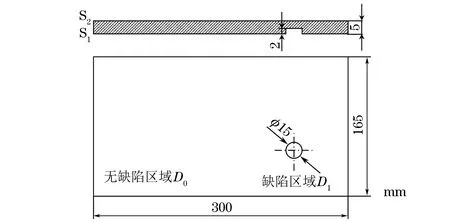
图2 试验件结构尺寸示意
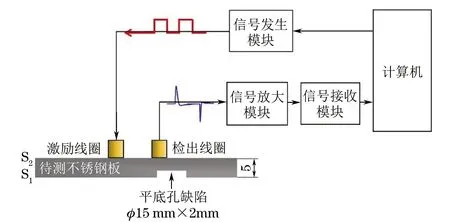
图3 试验系统框架
图3为试验用脉冲涡流检测系统构架,其主要由涡流检测探头(激励线圈,检出线圈)、信号发生模块、信号放大模块、信号采集与接收模块和计算机组成。信号发生器产生方波电压驱动激励线圈T在待检试件中产生感应涡流,被检出线圈R接收到,并经过信号放大、数字化处理后输送到计算机中进行分析。试验中,涡流检测探头置于试验件S2面,以随机点扫查的方式在无缺陷区域(D0)和缺陷区域(D1)分别采集50组数据,提取每组信号的峰值幅度、峰值时间、过零时间、主峰面积、衰减时间和峰值频率6个特征参数,两类区域的脉冲涡流信号特征分布如图4所示。
由图4可知,根据峰值幅度、过零时间和衰减时间等3个特征参数可以大致将样本分为两类,但特征参数的分布有少量重叠,在缺陷识别中存在误判的可能性;根据峰值时间和峰值频率两个特征参数也可基本区分缺陷与无缺陷,但特征参数的样本重叠相对较多,影响缺陷分类识别的准确率;主峰面积特征有大量重叠,这表明该特征参数对缺陷不敏感,无法直接用于缺陷的分类识别,在联合其他特征参数进行综合分析时可能会影响检测人员的判断,影响缺陷分类识别的效率。综上可知,试验中无法建立缺陷与脉冲涡流信号特征之间的直接映射关系,因而采用单一特征参数进行分析无法保证缺陷分类识别的准确性;同时,不同特征参数对缺陷分类识别的敏感程度不同,采用多个特征参数联合进行分析有利于提高缺陷分类识别的准确率,但可能影响分类识别的效率。
2.2 特征参数的主成分分析
相关分析主要是揭示变量之间线性相关的密切程度。相关系数rp的定义如(6)所示,其反映变量xi和xj间的相关关系。
rp=cov(xi,xj)/σxiσxj
(6)
式中:cov(xi,xj)为变量xi和xj的协方差;σxi和σxj分别为变量xi和xj的标准方差。
表1为100个脉冲涡流信号特征参数间的相关系数。由表1可知,部分特征参数间存在较强的相关性,例如峰值幅度与过零时间的相关系数达到0.902,与其他特征参数的相关系数在0.8左右,这表明特征参数之间存在着大量的信息冗余。
采用主成分分析对100个脉冲涡流信号的6个特征参数进行处理,构造了一个主成分特征,表达式为:
y=-0.978x1+0.841x2+0.952x3-
0.699x4+0.920x5-0.890x6
(7)
主成分的特征值、方差贡献率和累计方差贡献率如表2所示。由表2可知,特征值λ1大于1,表明主成分对数据信息的解释能力较强;主成分的方差贡献率与累计方差贡献率为78%,表明该主成分可以涵盖数据的绝大部分信息。
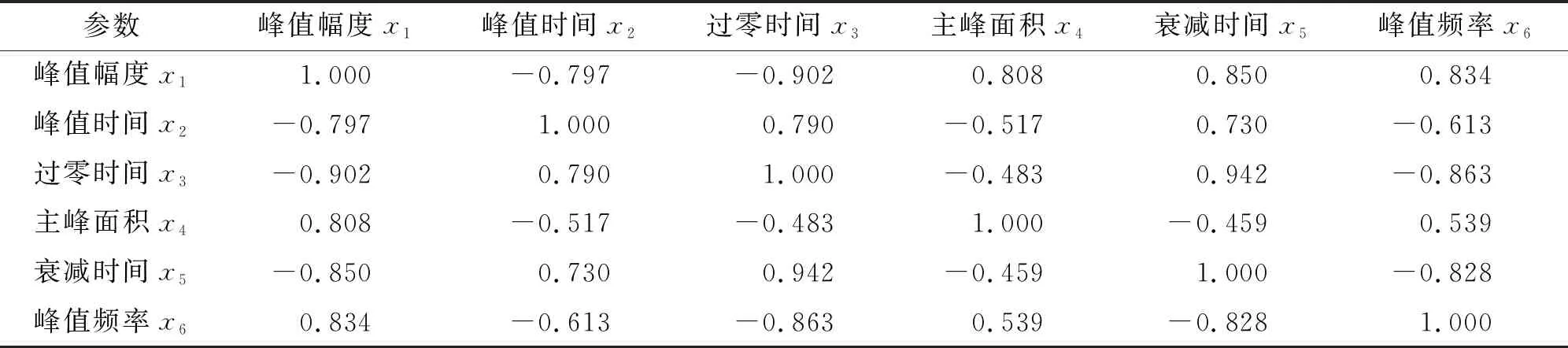
表1 脉冲涡流信号特征的相关系数

表2 脉冲涡流信号特征主成分方差贡献率
2.3 缺陷的Logistic分类识别
将100个样本的6个特征参数输入SPSS软件进行Logistic回归,得到如式(8)所示的判定方程:
P=[1+exp(9.19×1045x1+3.091x2+0.840x3+
0.465x4+0.334x5+2.152x6)]-1
(8)
基于式(8)进行缺陷识别,判定准确率为96%。将主成分特征输入SPSS软件进行Logistic回归,得到如下判定方程:

(9)
基于式(9)进行缺陷识别,判定准确率为93%。由此可见,采用主成分分析后数据量为原来的1/6,但是分类的准确率几乎不变,单位数据量对分类准确率的贡献大幅度提高。
3 结语
(1) 对脉冲涡流信号的峰值幅度、峰值时间、过零时间、主峰面积、衰减时间和峰值频率等6个特征参数进行相关性分析表明,各参数间存在较强的相关性。其中,峰值幅度与过零时间的相关系数达到0.902,峰值幅度与其他特征参数的相关系数大致在0.8,表明特征参数之间存在大量的信息冗余。
(2) 对上述6个特征参数进行主成分分析,构造了一个主成分特征,基于该主成分进行缺陷识别,准确率达93%;与6个特征参数分类的识别相比较,分类的准确率几乎不变,但是分类器处理的数据量仅为1/6,大大提高了分类器的缺陷识别效率,对于大规模的自动化检测具有积极意义。
(3) 主成分分析法将脉冲涡流检测信号的多个特征融合成一个主成分特征,同时保留了缺陷识别的关键信息,将大大减小工程检测中的数据分析与信息筛选难度。
