小学生数学学习阻碍及研学对策

梁远强

摘 要 本文通过心理学和教育学思惟学的观念，分析小学生出现数学研学阻碍的原因，分别从训养学习者学好数学的自信心创设愉悦的教学情境加强他们思惟能力训练等几方面，结合小学的数学研学内容实行阐述，探索小学数学的研学对策。

关键词 小学学习者 数学 阻碍 研学 策略

中图分类号：G623.25文献标识码：A

数学研学过程是一种复杂的知识归纳过程，学习者的非脑力要素和脑力要素会直接影响研学效果。在研学过程中如果能够针对学生学习阻挡并即时有目的地去引导，可以帮助有困难的学生获得学习上的成功。

1小学学习者在研学数学中形成阻碍的原因

心理学指出，智力囊括观察力记忆力思惟本领印象本领实践技术等根基成素。思惟立异本力是脑力要素的紧要中枢。非智力囊括念头乐趣意志和性情等根基要素。非脑力要素虽然是不直接参与研学进修，但对研学起到动力性和可持续性的感化。学习者对在数学研学中发生的拦阻，来源于如下几方面：

1.1心理阻碍

根据长期对数学成绩中下生的观察和调查发现，这部分学生心理上依赖性较强。课堂上依附老师，期待着老师把什么答案都说出来给他们知，完成作业时依靠同伴，遇上稍为复杂的题目，从来不去独立思考完成，而是急着想要同学的答案。较多的学习者没有形成对数学学习的兴趣和自信，认为研学数学不容易，自己不是研学数学的底子，碰到难题就马上不理。虽然他们内心上也希望学会，但他们更害怕接觸数学的学习，生怕学不会。这样下去，数学分数会愈来愈差，造成不好的轮回。

1.2思惟本力的阻延

数学研学进程是与思惟本身的应变力紧密相关联的。完小四、五、六年级学生正位于由具体思惟进阶到变通思惟的初级一段，思惟的跳跃还很难摆脱物体或它们的表象。如果所要解释的题目讲求抽象思维的总括程度，会越过他们已有的认知水平，从而产生思维阻碍现象。数学中涉及很多定义算理定律和特性等，如果他们在这些方面有知识缺陷，就一定会对新知识的学习造成思维阻碍。别的因思惟定势而发生负迁徙也易发生思惟拦阻。思惟本领的阻挡是研学中最紧要的负荷。

1.3空间知觉和想象本领上的拦阻

空间感和抽象力是数学研学，特别是图形方面研学的必备力。小学学习者中不少的人在某个面上的角边系列感知本领低，没形成好的空间维度，或者维度抽象本领较为落后。好比在研学圆柱侧面辗开这一课时，部分学习者会感觉不知道怎么样去想像或想像困难。

1.4注意力和记忆力相比较而言较弱是数学研学进程中阻挡出现的重要原因

实践证明，研学成功与意志力的集中度有关指数可高0.5以上。小学生的束缚本领不强，注意力的集中度不强，持续时间较短，堂上注意力涣散而导致研学阻碍。在堂上研学历程中，小学习者的识别记忆至紧要的是机本式识别技法。但靠机本式识别技法学概义、定律、特质等都是难以学好数学的。

2跨越阻碍的教学对策

针对学习者在学习数理时的那些阻碍，教学者在数学研学中可以采取下面的一些对策：

（1）在数学研学中给他们以创造修学乐成的进程，逐渐培养起学习者对学好数学的自信心。第一，每节都可以让学习者了解研学的详细目的。举个例子，在研学《平行四边形的面积》一课时，给出终成要点：①学明平行四边形面积的推导程况;②学得平行四边形的面积运算公式;③可以通过计算公式的运用来解答日常存在的实际问题。让他们在通过“学习进修过程”而达到目标后出现愉悦感。第二，在讲解知识时应注重量力性，使他们感受到付出努力就能解决问题。第三，对于识记点的理解查看或点评时，可符合学习者的实则本领，使他们领悟到付出与结果是同步的。

（2）给学习者创出乐学的研学程况，品行情境研学。赞科夫说：讲习法一旦触发学习者的情感和内心范围，触发学习者的精力方面，这种讲习法就会有高效性。讲习中建立轻快、调和的学习环境，落实师生情境的和谐和共识，使学习者处在愉悦的求学心态。第一老师应时常关心自己的学生，把对学生的爱深化到自身的情感中，让学生体会到和煦和愉悦;第二老师尽心把握教学的内容，新鲜风趣的内容，方式多样的教学呈现，准能引起学习者的关注，引发学生学习的动力，激发学生介入整个学习过程。例如讲解“三角形三条边的关系”（四年级下册）这一节，预习时可让学生预备5根小木条，长度分别为16cm，14.5cm，10.5cm，8.5cm，6.5cm。课堂上，老师可在已有知识的基础上提问：任意三条线段都能够围成一个三角形吗？老师让学习者按下列情况摆出三角形，分别观看它们的外形：①6.5cm、10.5cm、14.5cm ②6.5cm、8.5cm、10.5cm ③8.5cm、6.5cm、14.5cm ④6.5cm、16cm、8.5cm。接下来让学习者反思为什么有些组可以形成三角形，而有些组不可以呢，学习者在反思中领会△三条边的关系，得到：△任意俩边的和大过最后一边，任意俩边的差小于最后一边，从而使学习者轻松获得了研学乐成的愉悦感。

（3）增强小学生脑筋能力锻练，清除脑力阻碍。

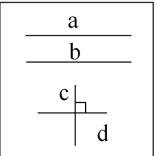
①凭借直觉讲授，召唤现象，搭建从具体现象到抽象思路的纽带。例如在教授四年级上册“平行与垂直”一课时，让学生课前准备一张白纸作为一个平面。上课时让学习者在该平面中画一条直线，并让他们闭目想象这条直线在伸长，遇着另一直线，叫学习者按想象把第二条线也在白纸上画出来，慢慢的，不同的学习者看到自己的一张白纸上出现俩线，有些互交形成一个交叉点，有些没有交叉点，分析得出：俩线在同一平面的位置系列有互交或不互交两类，然后老师在黑板上画出两类特殊状况：“平行”和“垂直”，引导学生观察并思考，得出“已知在一个面里，不交的俩线a和b，可表示为a∥b。直线c和直线d如果互交并且成的角是90度的，示为c⊥d。

②引发数学学科素养和研学方略的研学，激活学习者的数学脑力思惟。让学习者执掌数理思路比执掌数理基本识点会还紧要。例如在教学计算1.3？.33时（五年级上册），教师可引导学生思考：你们把它看作哪一个整数乘法了呢（出示整数乘法13？3=429的竖式），然后让学生观察对比：计算结果是多少？后来又怎么变成0.429的呢？最后教师小结方法：不单是你们适才运算的这个乘法算数题，还有我们屡次次算乘法算数题时可出现类似的整数乘法法则，它就似忍者那样，助它办成运算。

③使用学习模具，凭借多媒体课件讲解，运用简洁专业的教学用语可以激发学习者的空间思想能力。例如在讲习<展开圆柱侧面形>问题时，展开的侧面是个长方形，圆柱底面的周长对应是长，高对应是宽 ，可以借助具体的模型进行教学。在讲授“两直线位置关系”时，可以应用电脑模拟两条直线无限延长并出现不交叉、交叉、交叉且垂直的全过程等。用专业的数学术语进行解说，可以得到更好的成效。

④锻练学习者各方面的识记要领。举个例，在研学“圆椎的体积运算式”时，他们挑选一些等底等高的圆柱和圆椎，然后根据要求进行活动，在活动中，学习者获得了“圆柱体积是其等底等高的圆椎体积的3倍”的知识，从而得出“V椎=（1/3）V柱”的结果，通过他们亲身经历的研学活动所获取的识点会更牢固。又如，学习“圆柱侧面积运算”时，想理解记忆，首先要明白展开圆柱的侧面是什么图形，对应的边又是什么，理解了，学生自然明白圆柱的侧面积实际就是底面圆的周长乘以圆柱的高，因此，想提高成绩，关键是促进学生了解数学概义、公式、定律、性质等。

参考文献

[1] 向中军.让理性思维走进课堂教学[J].中学数学教学参考，2004（12）.

[2] 周莹.串联的智慧——以于萍老师小数乘法复习为例[J].新教师，2015（02）.