基于改进神经网络腐蚀管线剩余寿命预测

李颜 谢飞

摘      要： 为准确预测埋地油气管道腐蚀剩余寿命，构建基于改进神经网络腐蚀管线剩余寿命预测模型。首先，利用共轭梯度法对神经网络进行改进，保证目标函数在迭代n次之后找到全局极小点;其次，以国内某油田在役埋地原油管线为背景，确定影响因素;然后分析数据，采用拉依达准则对不良数据样本进行剔除，依据样本数据建立BP神经网络模型及共轭梯度法改进的神经网络模型;最后，以国内某油田在役埋地原油管线为实例，验证模型的预测有效性。结果表明：通过改进神经网络预测的管道剩余寿命预测结果与观测值基本相同，改进神经网络模型隐含层共计1个，平均相对误差为9.4%，预测结果更为精准，改进神经网络预测的管道剩余寿命误差更小。

关  键  词：腐蚀管线;剩余寿命预测;神经网络;共轭梯度

中图分类号：TE988       文献标识码： A       文章编号： 1671-0460（2020）11-2629-04

Prediction of Residual Life of Corroded Pipeline

Based on Improved Neural Network

LI Yan， XIE Fei

（College of Petroleum and Natural Gas Engineering， Liaoning Shihua University， Fushun 113001， China）

Abstract： In order to predict the corrosion residual life of buried oil and gas pipeline accurately， the residual life prediction model based on improved neural network was established. Firstly， the conjugate gradient method was used to improve the neural network to ensure that the objective function can find the global minimum point after n iterations; Secondly， the influencing factors were determined based on the in-service buried crude oil pipeline of an oil field in China; Then， the data were analyzed，and the Pauta Criterion was used to eliminate the bad data samples. Based on the sample data， the BP neural network model and the improved neural network model by conjugate gradient method were established; Finally， the effectiveness of the models were verified by an example of an in-service buried crude oil pipeline in an oil field in China. The results showed that the prediction result of pipeline residual life predicted by improved neural network was basically the same as the observed value. There was one hidden layer in the improved neural network model with an average relative error of 9.4% ，and the prediction result was more accurate，the structure of the model was simpler and the error was smaller.

Key words： Corroded pipeline; Residual life prediction; Neural network; Conjugate gradient

管道運输作为主要运输方式之一，已有百年历史。我国石油天然气工业发展越来越迅猛，各行业的发展都离不开石油和天然气，石油天然气管道输送在我国国民经济中占有极为重要的战略地位。我国作为发展中国家，油气管道是经济发展动脉，同时在役长输管道安全运行也与人民生活、国家形象等息息相关。在管道投入运行的后期，管道因腐蚀破坏而造成的管体穿孔泄漏事故时有发生，油气管道发生事故的概率也会随着运行时间而急剧增加。我国的石油天然气管道中有一半以上已运行多年，泄漏事故频频发生。油气管道一旦发生泄漏事故，不但会造成严重的环境污染，还可能引起火灾或爆炸等重大的安全事故，同时造成重大的直接或间接的经济损失。管道因管体腐蚀而发生泄漏已成为输油管道运行的主要故障，会严重干扰正常的生产运行[1]。因此，无论考虑经济价值还是社会意义，评价管道安全性、开展管道剩余寿命预测研究，都有着重要意义。

目前，针对含腐蚀缺陷管道的剩余强度评价及管道剩余寿命预测研究，国内外学者通过大量研究提出了各种规范和标准。20世纪60年代末，美国德克萨斯州东部输气公司和美国天然气协会共同提出了B31G准则，1989年美国天然气协会再次进行研究修正得到Modified  B31G方法[2-3]，1999年英国燃气公司（BG）和挪威船级社联合开发了针对带有腐蚀缺陷的管道剩余强度评价的DNV RP-F101标准[4]和用于评价含钝口腐蚀缺陷中高强度管道的PCORRC方法[5]。这些方法基本采用了半经验断裂力学公式来计算管道失效压力。但是随着实际工程应用的经验积累、力学分析能力的提高和无损检测手段的发展，从中发现这些评价方法存在较大的安全富余量和一定的保守性[6]。影响管道剩余寿命因素众多，各因素相互影响，呈现非线性等特点，故精准预测腐蚀管道的剩余寿命较为复杂。

综上所述，笔者针对输油管道剩余寿命预测研究的特点，考虑利用神经网络自组织、自学习、能拟合非线性函数等功能[7]，结合某油田原油管道实地勘测数据，预测管道剩余寿命。同时，采用共轭梯度算法改进神经网络，加快计算速度及计算精度。最终，得到预测管道剩余寿命可靠数学模型。

1  改进神经网络预测模型

1.1  神经网络

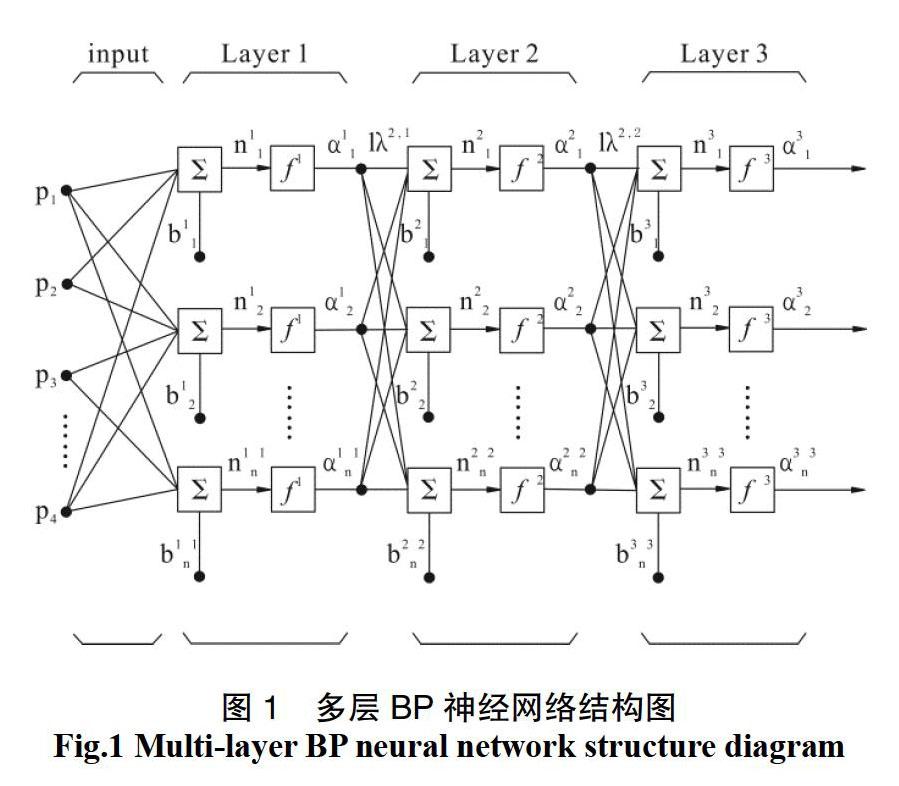
1956年， Rumelhart和MCclelland 初次提出BP神经网络，该神经网络属于多层前馈神经网络。BP神经网络学习算法也被称为梯度下降算法，该算法的目标函数是误差平方值函数。此学习方法是根据负梯度下降方向从而不断调整神经网络间的各权值和阀值以使得目标函数训练误差最小。BP神经网络学习算法属于有指导训练的前馈多层网络训练算法，可以通过调节从输入层到输出层各层的权重，使得神经网络对训练数据进行学习[8]，该网络广泛应用于非线性函数拟合、模式识别、大数据聚类等场合[9-10]。

多层BP神经网络由多个神经元构成，具体构造如图1所示。

其中： ;

;

。

最终输出为：

。

1.2  共轭梯度法改进神经网络

共轭梯度法主要利用一阶导数，不仅克服传统梯度下降法收敛慢的缺点，而且避免牛顿法对存储高和计算Hesse矩阵并求逆等缺陷，共轭梯度法是解大型非线性最优化最有效的算法之一。采用共轭梯度法改进BP神经网络，使得模型具有所需存储更小，收敛性快，稳定性高等优点。

其思路为对一个目标函数 ，找到一组方向向量 ，依次按此方向组中的方向对迭代点 进行更新，对每一个更新方向 ，找到合适的步长 ，使得 在该方向上取得最小值。要求在每一个新的更新方向 对迭代点 进行更新时，不会影响在之前方向 上的更新结果，即 不仅使 在 方向上取得最小值，且在 方向上均保持最小值。如果能找到这样一组方向 ，那么可以保证在迭代 次之后找到 的全局极小点。

1.3  模型效果校验

用平均相对误差 和决定系数R2等2个指标检验模型预测效果，见下列公式：

;

;

;

;

;

。

式中： m —检验数据个数;

—第k年的腐蚀速率实测值， mm·a-1;

—第k年的腐蚀速率预测值，mm·a-1。

相对误差 越小，说明预测精度越高;决定系数R2越接近1，说明神经网络拟合效果越好，越接近0，说明拟合效果越差。

2  原油管道剩余寿命预测

选取某油田在役原油管线的同管径、不同管段的实地勘测的历史数据，共64组。该组管线通径为DN300，设计压力等级为Class300，壁厚系列为SCH60，材质为20#碳钢。实地勘测的历史数据包括土壤参数，如pH、水溶性氯离子、硫酸根离子、O2、Ca2+、Mg2+、Cl-、CO2、H2S、Fe等;工艺参数，如操作压力、操作温度等;以及通过经验计算的观测剩余寿命。

2.1  数据处理与分析

2.1.1  数据处理

由于数据勘测过程中受到勘测设备、勘测方式、勘测人员业务水平等因素影响，数据存在异常、噪声干扰等不良特征，该类数据危害神经网络建模过程，因此需对原始数据进行预处理。

数据预处理主要为不良样本剔除，具体采用拉依达准则，即一组样本数据 ，若存在偏差>3 的样本，考虑剔除，其中：

。

2.1.2  数据相关性分析

相关性分析旨在取消与管道剩余寿命不相关或者关联度较小数据类型，筛选出重要影响因素，相关性分析还可有效减少输入样本维度，加快神经网络训练速度，有利于建模过程。

采用偏相关方法分析数據相关性，偏相关分析方法是指当两个变量同时与第三个变量相关时，可以将第三个变量的影响剔除，只需要分析另外两个变量之间相关程度的过程，判定指标是相关系数的 值。

值是针对原假设 是假设两变量无线性相关而言的。一般假设检验的显著性水平为0.05，只需要拿 值和0.05进行比较：如果 值小于0.05，就拒绝原假设 ，说明两变量有线性相关的关系，他们无线性相关的可能性小于0.05;如果大于0.05，则一般认为无线性相关关系，至于相关的程度则要看相关系数 值， 越大，说明越线性相关， 越小，则线性相关程度越低。

经过上述过程后数据样本如表1所示。

2.2  建立BP神经网络模型及共轭梯度法改进神经网络模型

选取pH、硫酸根离子、水溶性氯离子、Cl-、O2、Ca2+、Mg2+、Fe、CO2、H2S、操作温度、操作压力数据作为神经网络输入，观测剩余寿命作为神经网络输出，将数据分别导入BP神经网络模型及共轭梯度法改进神经网络模型进行训练。

其中，输入输出层选取线性激活函数：

。

隐含层激活函数选取（0，1）内连续、单调、可微分的Sigmoid非线性函数：

。

并将50组勘测样本数据分为两组，72%用于训练神经网络模型，28%用于测试神经网络模型。

同时，为了避免数据样本数值过大，防止神经网络计算量过大而所引起模型的“瘫痪”，对50组勘测样本数据进行归一化处理。数据归一化处理按照如下方法进行：

。

其中： —样本数据中最小值;

—样本数据最大值;

—样本数据;

—归一化后数据。

将归一化后的勘测样本数据分别导入BP神经网络模型及共轭梯度法改进神经网络，完成建立模型与测试。

2.3  模型对比

经软件计算后，共轭梯度法改进神经网络模型隐含层共计1个，平均相对误差为9.4%，决定系数R2为0.76;BP神经网络模型隐含层共计2个，平均相对误差为10.5%，决定系数R2为0.69。

经对比，共轭梯度改进神经网络模型误差较小，决定系数R2更加接近1，拟合及预测结果较好。BP神经网络模型及共轭梯度法改进神经网络模型预测结果对比曲线详见图2。

3  结 论

通过BP神经网络模型及共轭梯度法改进神经网络模型预测结果对比曲线可以知道，无论是通过改进的神经网络模型预测的管道剩余寿命，还是通过BP神经网络模型预测的管道剩余寿命，其预测结果均与观测值的趋势基本相同，这两种方法均可以对管道剩余寿命进行预测，改进的管道剩余寿命神经网络预测模型结构更为简单，隐含层数相对更少，这样就提高了运算速率，且使得误差更小，拟合度更优。由此可见，利用共轭梯度法改进神经网络较传统BP神经网络在预测管道剩余寿命效果上更好。

随着计算机软件的不断发展、功能不断完善及其可视化的界面日益人性化、简洁化，如今建立神经网络已经不再需要编写繁琐的程序语言，诸多软件公司均推出了其独有的神经网络工具箱（如Matlab神经网络工具箱、SPSS神经网络分析工具等），使得神经网络建模与预测更加简易、快捷。通过此类软件进行剩余管道寿命预测，可以更方便地了解在役管道的运行情况，对预防管道泄漏及破裂有一定的参考价值。

参考文献：

[1]王齐，胡林林.基于BP神经网络的油气长输管道土壤腐蚀性预测[J]. 当代化工，2016，45（9）：2198-2200.

[2]朱涛.ASME B31G系列评价方法的演进及影响因素研究[J].当代化工，2016，45（10）：2466-2469.

[3]The American Society of Mechanical Engineers. ANSI/ASME   B31G—1984.Manual  for  determining  the  remaining  strength  of  corroded pipelines[S]..

[4]DNV RP-F101，Recommended practice RP-F101 corroded pipelines [S].

[5] 帅健，张春娥，陈福来.腐蚀管道剩余强度评价方法的对比研究 [J].天然气工业，2006，26（11）：122-125.

[6]杨茜. 压力管道腐蚀缺陷的非线性有限元分析[D]. 西安：西安石油大学，2014.

[7]LIAO  K， YAO  Q， WU  X， et  al. A  numerical  corrosion  rate  prediction method  for  direct  assessment  of  wet  gas  gathering  pipelines  internal corrosion[J]. Energies， 2012， 5（10）： 3892-3907.

[8]李綿升. 基于粒子群与控制误差回馈的BP神经网络冷负荷预测及动态目标控制[D]. 广州：华南理工大学，2012.

[9]王幸运，贾瑛，许国根，等.人工神经网络-遗传算法优化化学镀四元合金工艺 [J].当代化工，2013，42（1）：73-75.

[10]陈戈珩，程青青.基于人工神经网络的字母识别[J].长春工业大学学报，2019，40（1）：31-37.