石油与天然气工程挑战性课程教学实践

摘 要 本文给出了我校《海洋油气集输》课程中计算机编程项目的详细求解方法及参照答案，这些计算机编程项目在教学中应用效果良好，能够有效的帮助学生掌握油气集输课程的重要的理论，同时发展学生解决实际工程问题的能力。现将实践教学中使用的编程项目的解法及参考答案整理成文，方便相关专业的广大师生在本科教学过程中使用。

关键词 油气集输 编程项目 算例 闪蒸计算 管网计算

中图分类号：G642文献标识码：A

在《石油与天然气工程挑战性课程教学实践——海洋油气集输计算机编程项目设计》一文中，介绍了中国石油大学（北京）在海洋油气集输全英文教学改革过程中使用的计算机编程项目的内容设计和教学效果，本文详细给出了三个计算机编程项目的求解方法和算例，以便开设类似课程的大专院校使用或在此基础上对教学内容做进一步改进。

1计算机编程项目1（Computer Project 1， CP1）：采用DAK方程进行天然气压缩因子计算

采用DAK方程进行天然气压缩因子计算的基本原理请参见文献[1][2]。现给出算例如下：

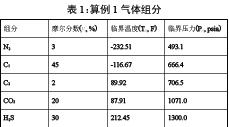
算例1：设气体温度为103.73F（313K），摩尔分数如下表（冯叔初等，2006;例2-3， p.101）。求：压力为1015.264psia（7.0MPa）时的气体压缩因子？

注：表中气体摩尔分数取自冯叔初等;临界温度、临界压力取自Ahmed;R = F + 459.67。

【解】：

第1步：计算拟临界温度（）、拟临界压力（）：;;注意在所有的计算过程中，温度均需采用绝对温标：热力学温标（K）或朗肯温标（R），本文使用朗肯温标。

第2步：如果天然气组分中不含CO2和H2S，则直接跳至第3步。本例中，CO2和H2S组分的存在会使得天然气压缩因子偏离Standing-Katz压缩因子图（即DAK方程原始参考数据），Wichert和Aziz提出了一种针对酸气拟临界参数（和）的修正方法，使得经过修正后的酸气压缩因子符合Standing-Katz压缩因子图。对于朗肯温标，Wichert和Aziz对拟临界温度的修正量可表示为：

（1）

此表达式与温标的选取有關（对于开氏温标：）。式（1）中代表CO2和H2S在天然气中总的摩尔分数;B代表H2S在天然气中的摩尔分数。本例中，

第3步：计算拟对比温度（）、拟对比压力（）：;。将所得的与代入目标函数（参文献[1]中式（6）），形成以为唯一未知量的方程。采用牛顿法对其进行数值求解（参文献[1]中式（7）），求得（表2给出了详细的迭代计算结果）：

表2：DAK状态方程求解压缩因子计算迭代结果

意味着初始迭代时需给出的初始值，由参文献[1]中式（4）可得， （取压缩因子;临界压缩因子）。注：表2在计算时，收敛标准设为

;

第4步：参文献[1]中式（4），

。

在进行CP1要求的天然气压缩因子图（参文献[1]，图1、图2）计算时，在给定的值下，取的取值范围为[0，15]即可做出不同下的天然气压缩因子曲线;此外，将换算为即可得到压缩因子与的关系曲线。

2计算机编程项目2（Computer Project 2， CP2）：二级地面油气分离系统闪蒸计算

算例2：CP2的主要教学任务和教学目标参见文献[1]。

【解】求解CP2时，需要对每个分离器分别实施闪蒸计算。在完成闪蒸计算程序时，需要采用模块化的编程思想将任务分解：（1）编写一个求解立方形状态方程的子函数;（2）编写一个求解Rachford-Rice目标函数的子函数;（3）编写一段代码更新平衡常数，调用前两个子函数完成相平衡计算。具体求解过程如下：

第1步：求解立方形状态方程（编写Zfactor子函数）。

流体系统的PVT关系由状态方程表述。Peng-Robinson状态方程（PR EOS）和Soave-Redlich-Kwong状态方程（SRK EOS）是目前工业界使用最广泛的立方形状态方程，其表达式分别如下：

（2）

（3）

式（2、3）中，为压力（psia），为温度（R），为摩尔容积（ft3/lbmol），为通用气体常数10.73 ;和分别为状态方程相对于混合物的引力项和斥力项参数，可由纯组分参数（）和相应的混合规则计算得到：

（4）

（5）

（6）

（7）

式（4-7中），分别为状态方程对于第种组分对应的纯组分物质的引力项和斥力项参数;代表混合物中组分的数量;和是纯组分参数，对于，;对于，;为混合物体系中第种组分的摩尔分数;和为混合物体系中第种组分的临界温度和临界压力;为混合物中第种组分和第种组分间的二元相互作用参数（Binary interaction parameter，BIP）;为第种组分的对比温度（）;为与纯组分偏心系数（）有关的表达式，对于PR EOS和SRK EOS分别如式（8.1）和式（8.2）所示：

（8.1）

（8.2）

在石油和天然气行业的应用中，立方形状态方程常常表示为压缩因子（z）的形式，根据实际气体状态方程，式（2、3）可分别改写为：

（9）

（10）

其中，

;                                                             （11）

Coats进一步指出式（9）和（10）可以写成统一的形式：

（12）

式（12）中，对于，;对于。求解式（12）的过程就是求三次方程的根。在教学实践中，理解根的选择是个教学难点。三次方程必然有三个根，但对于给定的温度、压力、组分的体系，只对应一个具有物理意义的压缩因子，需要在求解的三次方程时进行根的选择（参图1）。

图1中，在温度下，立方型状态方程反映的P-v变化关系如图中较粗的黑色曲线所示，该曲线在气液两相区内分别与泡点线交于A点并与露点线交于E点。AE水平连线对应的压力（即为温度下的饱和蒸汽压。A、E点分别对应“可能的”液相或气相摩尔容积和，“可能的”意味着在求解时，我们通常并不预先知道所给定的混合物是以气相还是液相存在。图中C点位于曲线BCD段上，该段曲线上，有，说明在该段曲线上对于闭口系统容积增大压力也增大，不符合实际情况;因此C点处对应的摩尔容积仅仅是一个数学意义上的解，没有实际的物理意义，在求解立方形状态方程时应当舍去。

此时，在剩下的两个具有物理意义的解和中，必须再舍弃一个，因为在计算过程中针对液相（）或气相（）组分进行计算最终只能有一个具有物理意义的实根。通常有如下两种处理方式：

如果预先知道计算过程针对的是气相组分（），此时式（4）和式（5）中：，图1中和两个根选择较大的根;对应式（12）的解也选择较大的根，。如果预先知道计算过程针对液相组分（），此时式（4）和式（5）中：，对应式（12）的解也选择较小的根，即。

在两个具有物理意义的根（和）中，直接比较二者得到的系统Gibbs自由能大小，因为系统总是倾向于处于最小Gibbs自由能的状态。Danesh指出：

（13）

式（13）大于零时，说明使得系统Gibbs自由能最小，取舍;反之，取。

验证压缩因子子程序计算的正确性。采用文献[1]中表3提供的原油组分及物性参数数据，将自行编写的压缩因子计算子程序的计算结果与下表验证后再进行下一步：

第2步：求解Rachford-Rice目标函数（编写VLE子函数）。

由气液相物料守恒可以推导得出Rachford-Rice目标函数具有如下形式：

（14）

式（14）中，为体系中第种组分在体系中总的摩尔分数;为体系达到平衡状态时的气化分率（气相中物质的量与体系中总物质的量的比值）;为第种组分的平衡常数，可由Wilson经验公式近似计算得到：

（15）

式中，，。由式（14-15）可见，在各组分平衡常数已知的情况下，式（14）中唯一的未知量便是气化分率，可采用数值解法（如：Newton-Raphson法）求解方程（14）得到气化分率：

（16）

当时停止迭代（为预先拟定的收敛标准）。在迭代计算过程中，需要给赋初值使得迭代计算开始（通常取），气化分率的计算值虽然可能超出实际取值区间[0，1]，只要其最终的计算结果在区间[0，1]之间即可，为了在气化分率超出实际取值区间时迭代计算仍然能够继续进行，在每一步迭代后都进行如下判断：

（17）

式（17）中，和分別为组分平衡常数的最大值和最小值。当迭代收敛后，气液相的平衡组分可由式（18-19）求出：

（18）

（19）

此时，我们得到了平衡气相组分（）以及平衡液相组分（）。通过采用气相或液相组分替代式（4-5）中的（），我们可以得到气相或液相的压缩因子。现采用文献[1]中表3提供的原油组分及物性参数数据，读者可将自行编写的程序运行结果与下表对照，验证求解Rachford-Rice目标函数的正确性;学生经与此表4内的提供的数据验证正确后，再进行下一步计算。

第3步：获得准确的平衡常数（编写MAIN程序）。

命名MAIN主程序，实施平衡常数更新。第2步计算的前提是平衡常数已知（由Wilson公式计算）。但是在实际的工程应用中，在特定的压力、温度和组分条件下，平衡常数的值往往并不能在一开始计算时就准确获得，Wilson经验公式只是较粗略的估算。准确的平衡常数需要根据相平衡理论反复迭代更新后才能得到。

当体系中气液两相处于平衡状态时，相间各组分逸度相等，可表示为：

（20）

式（20）表示含有种组分的混合物体系处于气液两相平衡时，任意第种组分在气相和液相中的逸度相等（上标L表示液相;V表示气相）。通过逸度的定义（）以及平衡常数的定义，可得：

（21）

当且仅当时，式（21）表示体系的平衡常数，因此可用连续迭代法（式22）对计算中求得的平衡常数进行更新：

（22）

在迭代开始时，需要给平衡常数赋初值，该初值往往由Wilson公式（式15）估算得到。在迭代过程中，当满足如下收敛标准时（式23）停止迭代，认为平衡常数已不再变化。

（23）

由式（22）可以看出，平衡常数由逸度系数计算更新得到，而气液相的逸度系数（）经过严格的热力学推导可由状态方程得到（式24）：

（24）

式中，

（24.1）

（24.2）

（24.3）

（24.4）

（24.5）

注意在应用式（24，24.3，24.5）时，要注意对于气、液相来说，需分别带入气相组分（）或液相组分（）进行计算。图2给出了CP2闪蒸计算主程序MAIN的算法流程图。

表5给出了在一定的温度和压力条件下，采用文献[1]中表3提供的原油组分及物性参数数据、依照图2流程计算获得的计算结果，如果学生自行编程计算的结果与下表各项数据吻合，则说明闪蒸计算流程及程序运行均正确无误。

第4步：将步骤1至3中获得的闪蒸计算程序应用至2级分离计算（参文献[1]CP2主要内容）中，计算储罐中原油收率、产出液气油比（GOR）、产出原油API重度等数据。

（1）储罐中原油收率：

假设1磅摩尔（1lbmol = 453.5924mol）井流进入高压分离器，由计算知经高压分离器后得到0.5882磅摩尔液相原油;该部分原油再进入中压分离器，闪蒸分离后得到0.4931磅摩尔原油;该部分原油进入储罐后，在标况下闪蒸分离后最终得到0.4821磅摩尔原油。由此可见，1磅摩尔井流最终在储罐中得到0.4821磅摩尔原油，则储罐中原油收率为48.2%。各级分离器闪蒸分离的计算结果如图3所示。

（2）产出液气油比（GOR）：

气油比可以定义为产出气的總体积（SCF， standard cubic feet）与储罐中得到的原油体积（STB， stock tank barrel）之比。即：

（25）

式（25）中表示气体在标况下的体积;为原油在储罐中的容积，由实际气体状态方程可得：

（26）

其中为原油在储罐中的摩尔数（lb-mol）;为原油在储罐条件下的压缩因子;和分别为储罐的温度（R）和压力（psia）。式（26）计算出的原油体积单位为SCF，转化为STB需要除以5.615（1STB = 5.615SCF）。此外，假设产出气在标况（14.7psia， 60F）下可用理想气体近似，1磅摩尔的气体具有379.4SCF的体积，得：

（27）

式（27）中，代表经各级分离器分离出气体得总摩尔数。将式（26-27）带入式（25）可得：

（28）

结合图3中计算结果，，，带入式（28），得到（SCF/STB）。

（3）储罐原油API重度：

从实际气体状态方程，可得：

（29）

（30）

式中，为油水比重;为储罐中原油的平均分子量;水密度（）取为62.4lbm/SCF，液相压缩因子由闪蒸计算得到，则本例得到的结果为，为轻质原油。

3计算机编程项目3（Computer Project 3， CP3）：天然气管网管段流量及节点压力计算

本例中管网系统求解时，要求学生分别使用两种解法：（1）Q-formulation：以管段流量为未知数求解;（2）P-formulation：以节点压力为未知数求解。如图4所示（假设节点压力已知）：

图4：管网样例（N：节点;B：管段;L：闭环;S：气源;D：用气）

对于任意给定的天然气管网稳态流动过程，（1）其每个节点处流量守恒（流入节点流量等于流出节点流量）;（2）如气流形成封闭环路，规定环路方向后（顺时针或逆时针）则环路中各管段的压力差之和为零。数学表达式如下：

（对所有节点）                        （31）

（对管流环路）                               （32）

Q-formulation法：图4中，当采用管段流量（）为未知数求解管网问题，将管流方程写成如下形式：

（33）

对于管网中每个节点依照式（31）可列方程如下：

节点：                                      （34.1）

节点：                                                 （34.2）

节点：                                 （34.3）

节点：                                      （34.4）

考虑到，式（34.4）其实是式（34.1至34.3）的线性组合（式（34.4）=式（34.1）+式（34.2）+式（34.3）），说明式（34.1至34.4）中，只有3个独立方程，而未知量却有5个，因此仍需要两个独立方程求解方程组。观察图4中的管路形成了2个闭环（假设气流在闭环内以顺时针方向流动）：L1和L2;对每个闭环依照式（32）可列方程如下：

闭环：                   （35）

闭环：                  （36）

式（35、36）中采用式（33）将各管段的压降转换为管段阻力与流量的表达式;当假设的管段流动方向与闭环的流动方向相反时，表示压降需添加负号。联立式（34.1至34.3）和（35-36）得到如下方程组（未知量）：

（37.1）

（37.2）

（37.3）

（37.4）

（37.5）

若记，由多变量牛顿法可得：

（38）

式（38）中，为Jacobian矩阵：

（39）

在用式（38）进行计算时，需要提供的初始值。各管段流量的初始值一般根据节点流量和管段阻力加以估算，例如：图4中计算初始值可估算如下：;;;;。在进行迭代时，可将循环收敛标准定为当向量（）中的最大元素小于。管段流量算出后，结合已知管网中某节点的压力，可由式（33）解出官网中各节点的压力。

P-formulation法：直接以管道中的节点压力作为未知量进行求解。将管流方程写成如下形式：

（40）

由式（31）列出任意三个节点的方程如下：

节点

（41.1）

节点：  （41.2）

节点：

（41.3）

由于节点压力已知，方程组（41）中含有三个方程、三个未知量（，，），可直接用牛顿法求解。该法看似较Q-formulation法简单，但对于气体管网，方程的非线性很强，且对初值的选取非常敏感，直接求解可能会遇到不能收敛的问题。对此法的改进本文不做阐述，感興趣的读者可参阅文献[15]。

在使用通用性管流方程（Generalized）时，需要采用Colebrook公式求解Moody管道摩擦系数：

（42）

式（42）中，为管道绝对粗糙度，in;为管径，ft;为雷诺数：

（43）

式（43）中，为气体比重;为流量，MMSCFD;为气体粘度，cp。当采用牛顿法求解管道摩擦系数时，初始值可以令式（42）中的为无限大计算得到。结合上述求解方法，针对CP3给出的几个稳态工况下的气体管网案例，现给出节点压力及管段流量参考解。

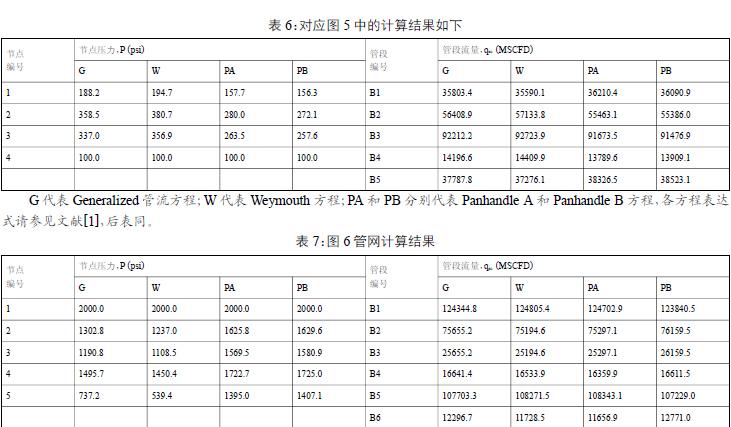
算例3：管网系统及假设的管段流动方向如图5所示（管道及气体参数见文献[1]）

【解】：

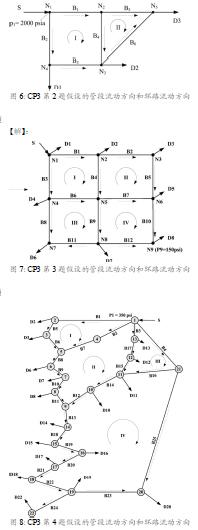
算例4：管网系统及假设的管段流动方向如图6所示（管道及气体参数见文献[1]）

【解】：

算例5：管网系统及假设的管段流动方向如图7所示（管道及气体参数见文献[1]）

【解】：

算例6：管网系统及假设的管段流动方向如图8所示（管道及气体参数见文献[1]）

【解】：

4总结

本文给出了我校海洋油气工程专业的本科生《海洋油气集输》挑战性课程计算机编程项目的详细求解方法和参照答案。该套编程项目对于中国石油大学（北京）大三的同学独立完成存在一定困难，但在教学中取得了大多数学生的理解和认可。本文所述的求解方法能够帮助学生更好的完成相关教学环节，在独立完成这些教学环节之后，学生不但能够感受到自己在计算、分析及应用能力上的进步，同时也对所学的内容理解更加透彻。

基金项目：中国石油大学（北京）教育教学改革项目“海洋油气集输全英文核心课程建设”。

参考文献

[1] 赵海宁.石油与天然气工程挑战性课程教学实践——海洋油气集输计算机编程项目设计[J].化工高等教育，2019，36（06）：40-50.

[2] Dranchuk，P.M.and Abou-Kassem，J.H.Calculation of Z factors for natural gas using equations of state[J]. Journal of Canadian Petroleum Technology，1975，14（03）：34-36.

[3] 冯叔初，郭揆常等.油气集输与矿场加工（第二版）[M].中国石油大学出版社，2006.

[4] Ahmed，T.Equations of state and PVT analysis applications for improved reservoir modeling， 2nd edition[M].Gulf Professional Publishing，2016.

[5] Standing，M.B.&Katz，D.L.Density of natural gases[J].Pet. Trans.AIME，1942（146）：140-149.

[6] Wichert， E.&Aziz，K.Calculation of Z's for sour gases[J].Hydrocarbon Processing，1972，51（05）：119-122.

[7] Rachford Jr. H.H.&Rice，J.D.Procedure for use of electronic digital computers in calculating flash vaporization hydrocarbon equilibrium[J].Pet. Trans. AIME，1952（195）：327-328.

[8] Peng， D.-Y.&Robinson，D.B.A new two-constant equation of state[J].Industrial Eng. Chem. Fundam，1976，15（01）：59-64.

[9] Soave，G.Equilibrium constants from a modified Redlich-Kwong equation of state[J].Chemical Engineering Science，1972（27）：1197-1203.

[10] Coats，K.H.Simulation of gas condensate reservoir performance[J].Journal of Petroleum Technology，1985，37（10）：1870-1886.

[11] Danesh，A.PVT and phase behaviour of petroleum reservoir fluids[M].Elsevier，1998.

[12] Wilson，G.A modified Redlich-Kwong Equation of state[A].Application to general physical data calculations [C].American Institute of Chemical Engineers National Meeting，1968.

[13] Whitson，C.H.&Michelsen，M.L.The negative flash[J].Fluid Phase Equilibria，1989（53）：51-71.

[14] Essenfeld，D.Network modeling and tracking of liquid preferential routes in natural gas pipeline systems [D].Master Thesis，The Pennsylvania State University，2010.

[15] Ayala， L.F.&Leong，C.Y.A robust linear-pressure analog for the analysis of natural gas transportation networks[J].Journal of Natural Gas Science and Engineering，2013（14）：174-184.

[16] Colebrook，C.F.Turbulent flow in pipes， with particular reference to the transition region between smooth and rough pipe laws[J].Journal of the Institution of Civil Engineers，1939，11（04）：133-156.

[17] Moody，L.F.Friction factors for pipe flow[J].Trans.ASME，1944（66）：671-684.